0^# and some forcing principles

Extract

It has been considered desirable by many set theorists to find maximality properties which state that the universe has in some sense “many sets”. The properties isolated thus far have tended to be consistent with each other (as far as we know). For example it is a widely held view that the existence of a supercompact cardinal is consistent with the axiom of determinacy holding in L(R). This consistency has been held to be evidence for the truth of these properties. It is with this in mind that the first author suggested the following:

Maximality Principle If P is a partial ordering and G ⊆ P is a V-generic ultrafilter then either

• a) there is a real number r ∈ V [G] with r ∉ V, or

• b) there is an ordinal α such that α is a cardinal in V but not in V[G].

This maximality principle applied to garden variety partial orderings has startling results for the structure of V.

For example, if for some 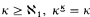, then P = 〈{p: p ⊆ κ, ∣p∣ < κ}, ⊆〉 neither adds a real nor collapses a cardinal. Thus from the maximality principle we can deduce that the G. C. H. fails everywhere and there are no inaccessible cardinals. (Hence this principle contradicts large cardinals.) Similarly one can show that there are no Suslin trees on any cardinal κ. These consequences help justify the title “maximality principle”.

Since the maximality principle implies that the G. C. H. fails at strong singular limit cardinals it has consistency strength at least that of “many large cardinals”. (See [M].) On the other hand it is not known to be consistent, relative to any assumptions.