Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T22:08:41.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Zonally dominated dynamics and Dimits threshold in curvature-driven ITG turbulence

Part of: Focus on Fusion Invited Contributions from the 18th European Fusion Theory Conference

Published online by Cambridge University Press:  27 October 2020

Plamen G. Ivanov Open the ORCID record for Plamen G. Ivanov [Opens in a new window] ,
A. A. Schekochihin Open the ORCID record for A. A. Schekochihin [Opens in a new window] ,
W. Dorland Open the ORCID record for W. Dorland [Opens in a new window] ,
A. R. Field  and
F. I. Parra
Plamen G. Ivanov*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK St John's College, OxfordOX1 3JP, UK EURATOM/UKAEA Fusion Association, Culham Science Centre, AbingdonOX14 3DB, UK
A. A. Schekochihin
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK Merton College, OxfordOX1 4JD, UK
W. Dorland
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK Department of Physics, University of Maryland, College Park, MD20740, USA
A. R. Field
Affiliation:
EURATOM/UKAEA Fusion Association, Culham Science Centre, AbingdonOX14 3DB, UK
F. I. Parra
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK Worcester College, OxfordOX1 2HB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

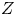The saturated state of turbulence driven by the ion-temperature-gradient instability is investigated using a two-dimensional long-wavelength fluid model that describes the perturbed electrostatic potential and perturbed ion temperature in a magnetic field with constant curvature (a $Z$-pinch) and an equilibrium temperature gradient. Numerical simulations reveal a well-defined transition between a finite-amplitude saturated state dominated by strong zonal-flow and zonal temperature perturbations, and a blow-up state that fails to saturate on a box-independent scale. We argue that this transition is equivalent to the Dimits transition from a low-transport to a high-transport state seen in gyrokinetic numerical simulations (Dimits et al., Phys. Plasmas, vol. 7, 2000, 969). A quasi-static staircase-like structure of the temperature gradient intertwined with zonal flows, which have patch-wise constant shear, emerges near the Dimits threshold. The turbulent heat flux in the low-collisionality near-marginal state is dominated by turbulent bursts, triggered by coherent long-lived structures closely resembling those found in gyrokinetic simulations with imposed equilibrium flow shear (van Wyk et al., J. Plasma Phys., vol. 82, 2016, 905820609). The breakup of the low-transport Dimits regime is linked to a competition between the two different sources of poloidal momentum in the system – the Reynolds stress and the advection of the diamagnetic flow by the 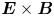$\boldsymbol {E}\times \boldsymbol {B}$ flow. By analysing the linear ion-temperature-gradient modes, we obtain a semi-analytic model for the Dimits threshold at large collisionality.

Keywords

fusion plasmaplasma nonlinear phenomenaplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 5 , October 2020 , 855860502
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abel, I. G. & Cowley, S. C. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: II. Reduced models for electron dynamics. New J. Phys. 15, 023041.CrossRefGoogle Scholar
Abel, I. G., Plunk, G. G., Wang, E., Barnes, M., Cowley, S. C., Dorland, W. & Schekochihin, A. A. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport and energy flows. Rep. Prog. Phys. 76, 116201.CrossRefGoogle ScholarPubMed
Abiteboul, J. 2012 Turbulent and neoclassical toroidal momentum transport in tokamak plasmas. Theses, Aix-Marseille Université.Google Scholar
Barnes, M., Parra, F. I. & Schekochihin, A. A. 2011 Critically balanced ion temperature gradient turbulence in fusion plasmas. Phys. Rev. Lett. 107, 115003.CrossRefGoogle ScholarPubMed
Beer, M. A. 1995 Gyrofluid models of turbulent transport in tokamaks. PhD thesis, Princeton University.Google Scholar
Calvo, I. & Parra, F. I. 2015 Radial transport of toroidal angular momentum in tokamaks. Plasma Phys. Control. Fusion 57, 075006.CrossRefGoogle Scholar
Catto, P. J. 2019 Practical gyrokinetics. J. Plasma Phys. 85, 925850301.CrossRefGoogle Scholar
Catto, P. J. & Simakov, A. N. 2004 A drift ordered short mean free path description for magnetized plasma allowing strong spatial anisotropy. Phys. Plasmas 11, 90.CrossRefGoogle Scholar
Catto, P. J. & Simakov, A. N. 2005 A new, explicitly collisional contribution to the gyroviscosity and the radial electric field in a collisional tokamak. Phys. Plasmas 12, 114503.CrossRefGoogle Scholar
Colyer, G. J., Schekochihin, A. A., Parra, F. I., Roach, C. M., Barnes, M. A., Ghim, Y.-C. & Dorland, W. 2017 Collisionality scaling of the electron heat flux in ETG turbulence. Plasma Phys. Control. Fusion 59, 055002.CrossRefGoogle Scholar
Cowley, S. C., Kulsrud, R. M. & Sudan, R. 1991 Considerations of ion-temperature-gradient-driven turbulence. Phys. Fluids B 3, 2767.CrossRefGoogle Scholar
Diamond, P. H., Itoh, S.-I., Itoh, K. & Hahm, T. S. 2005 Zonal flows in plasma—a review. Plasma Phys. Control. Fusion 47, R35.CrossRefGoogle Scholar
Dif-Pradalier, G., Diamond, P. H., Grandgirard, V., Sarazin, Y., Abiteboul, J., Garbet, X., Ghendrih, P., Strugarek, A., Ku, S. & Chang, C. S. 2010 On the validity of the local diffusive paradigm in turbulent plasma transport. Phys. Rev. E 82, 025401.CrossRefGoogle ScholarPubMed
Dif-Pradalier, G., Hornung, G., Garbet, X., Ghendrih, P., Grandgirard, V., Latu, G. & Sarazin, Y. 2017 The ExB staircase of magnetised plasmas. Nucl. Fusion 57, 066026.CrossRefGoogle Scholar
Dif-Pradalier, G., Hornung, G., Ghendrih, P., Sarazin, Y., Clairet, F., Vermare, L., Diamond, P. H., Abiteboul, J., Cartier-Michaud, T., Ehrlacher, C., et al. 2015 Finding the elusive ExB staircase in magnetized plasmas. Phys. Rev. Lett. 114, 085004.CrossRefGoogle ScholarPubMed
Dimits, A. M., Bateman, G., Beer, M. A., Cohen, B. I., Dorland, W., Hammett, G. W., Kim, C., Kinsey, J. E., Kotschenreuther, M., Kritz, A. H., et al. 2000 Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 7, 969.CrossRefGoogle Scholar
Dorland, W. & Hammett, G. W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B 5, 812.CrossRefGoogle Scholar
Dorland, W., Jenko, F., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient turbulence. Phys. Rev. Lett. 85, 5579.CrossRefGoogle ScholarPubMed
Frieman, E. A. & Chen, L. 1982 Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria. Phys. Fluids 25, 502.CrossRefGoogle Scholar
Frisch, U. 1995 Turbulence: The Legacy of A. N. Kolmogorov. CUP.CrossRefGoogle Scholar
Gentle, K. W. & He, H. 2008 Texas helimak. Plasma Sci. Technol. 10, 284.CrossRefGoogle Scholar
Hammett, G. W., Beer, M. A., Dorland, W., Cowley, S. C. & Smith, S. A. 1993 Developments in the gyrofluid approach to tokamak turbulence simulations. Plasma Phys. Control. Fusion 35, 973.CrossRefGoogle Scholar
Hasegawa, A. & Mima, K. 1978 Pseudo-three-dimensional turbulence in magnetized nonuniform plasma. Phys. Fluids 21, 87.CrossRefGoogle Scholar
Hasegawa, A. & Wakatani, M. 1983 Plasma edge turbulence. Phys. Rev. Lett. 50, 682.CrossRefGoogle Scholar
Helander, P. & Sigmar, D. J. 2002 Collisional Transport in Magnetized Plasmas. CUP.Google Scholar
Horton, W., Choi, D. & Tang, W. M. 1981 Toroidal drift modes driven by ion pressure gradients. Phys. Fluids 24, 1077.CrossRefGoogle Scholar
Horton, W. & Hasegawa, A. 1994 Quasi-two-dimensional dynamics of plasmas and fluids. Chaos 4, 227.CrossRefGoogle ScholarPubMed
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7, 1904.CrossRefGoogle Scholar
Kim, E. & Diamond, P. H. 2002 Dynamics of zonal flow saturation in strong collisionless drift wave turbulence. Phys. Plasmas 9, 4530.CrossRefGoogle Scholar
Kinsey, J. E., Waltz, R. E. & Candy, J. 2005 Nonlinear gyrokinetic turbulence simulations of ExB shear quenching of transport. Phys. Plasmas 12, 062302.CrossRefGoogle Scholar
Kobayashi, S. & Rogers, B. N. 2012 The quench rule, Dimits shift, and eigenmode localization by small-scale zonal flows. Phys. Plasmas 19, 012315.CrossRefGoogle Scholar
Kotschenreuther, M., Dorland, W., Beer, M. A. & Hammett, G. W. 1995 a Quantitative predictions of tokamak energy confinement from first-principles simulations with kinetic effects. Phys. Plasmas 2, 2381.CrossRefGoogle Scholar
Kotschenreuther, M., Rewoldt, G. & Tang, W. M. 1995 b Comparison of initial value and eigenvalue codes for kinetic toroidal plasma instabilities. Comput. Phys. Commun. 88, 128.CrossRefGoogle Scholar
Kuo, H. 1949 Dynamic instability of two-dimensional nondivergent flow in a barotropic atmosphere. J. Meteorol. 6, 105.2.0.CO;2>CrossRefGoogle Scholar
Majda, A. J., Qi, D. & Cerfon, A. J. 2018 A flux-balanced fluid model for collisional plasma edge turbulence: model derivation and basic physical features. Phys. Plasmas 25, 102307.CrossRefGoogle Scholar
McMillan, B. F., Hill, P., Bottino, A., Jolliet, S., Vernay, T. & Villard, L. 2011 Interaction of large scale flow structures with gyrokinetic turbulence. Phys. Plasmas 18, 112503.CrossRefGoogle Scholar
McMillan, B. F., Jolliet, S., Tran, T. M., Villard, L., Bottino, A. & Angelino, P. 2009 Avalanchelike bursts in global gyrokinetic simulations. Phys. Plasmas 16, 022310.CrossRefGoogle Scholar
McMillan, B. F., Pringle, C. C. T. & Teaca, B. 2018 Simple advecting structures and the edge of chaos in subcritical tokamak plasmas. J. Plasma Phys. 84, 905840611.CrossRefGoogle Scholar
Mikhailovskii, A. B. & Tsypin, V. S. 1971 Transport equations and gradient instabilities in a high pressure collisional plasma. Plasma Phys. 13, 785.CrossRefGoogle Scholar
Newton, S. L., Cowley, S. C. & Loureiro, N. F. 2010 Understanding the effect of sheared flow on microinstabilities. Plasma Phys. Control. Fusion 52, 125001.CrossRefGoogle Scholar
Numata, R., Ball, R. & Dewar, R. L. 2007 Bifurcation in electrostatic resistive drift wave turbulence. Phys. Plasmas 14, 102312.CrossRefGoogle Scholar
Parker, J. B. 2016 Dynamics of zonal flows: failure of wave-kinetic theory, and new geometrical optics approximations. J. Plasma Phys. 82, 595820602.CrossRefGoogle Scholar
Parker, J. B. & Krommes, J. A. 2013 Zonal flow as pattern formation. Phys. Plasmas 20, 100703.CrossRefGoogle Scholar
Parker, J. B. & Krommes, J. A. 2014 Generation of zonal flows through symmetry breaking of statistical homogeneity. New J. Phys. 16, 035006.CrossRefGoogle Scholar
Parra, F. I., Barnes, M. & Peeters, A. G. 2011 Up-down symmetry of the turbulent transport of toroidal angular momentum in tokamaks. Phys. Plasmas 18, 062501.CrossRefGoogle Scholar
Parra, F. I. & Catto, P. J. 2009 Vorticity and intrinsic ambipolarity in turbulent tokamaks. Plasma Phys. Control. Fusion 51, 095008.CrossRefGoogle Scholar
Parra, F. I. & Catto, P. J. 2010 Non-physical momentum sources in slab geometry gyrokinetics. Plasma Phys. Control. Fusion 52, 085011.CrossRefGoogle Scholar
Plunk, G. G. & Bañón Navarro, A. 2017 Nonlinear growth of zonal flows by secondary instability in general magnetic geometry. New J. Phys. 19, 025009.CrossRefGoogle Scholar
Plunk, G. G., Cowley, S. C., Schekochihin, A. A. & Tatsuno, T. 2010 Two-dimensional gyrokinetic turbulence. J. Fluid Mech. 664, 407.CrossRefGoogle Scholar
Qi, D., Majda, A. J. & Cerfon, A. J. 2019 A flux-balanced fluid model for collisional plasma edge turbulence: numerical simulations with different aspect ratios. Phys. Plasmas 26, 082303.CrossRefGoogle Scholar
Rath, F., Peeters, A. G., Buchholz, R., Grosshauser, S. R., Migliano, P., Weikl, A. & Strintzi, D. 2016 Comparison of gradient and flux driven gyro-kinetic turbulent transport. Phys. Plasmas 23, 052309.CrossRefGoogle Scholar
Ricci, P., Rogers, B. N. & Dorland, W. 2006 Small-scale turbulence in a closed-field-line geometry. Phys. Rev. Lett. 97, 245001.CrossRefGoogle Scholar
Rogers, B. N. & Dorland, W. 2005 Noncurvature-driven modes in a transport barrier. Phys. Plasmas 12, 062511.CrossRefGoogle Scholar
Rogers, B. N., Dorland, W. & Kotschenreuther, M. 2000 Generation and stability of zonal flows in ion-temperature-gradient mode turbulence. Phys. Rev. Lett. 85, 5336.CrossRefGoogle ScholarPubMed
Ruiz, D. E., Glinsky, M. E. & Dodin, I. Y. 2019 Wave kinetic equation for inhomogeneous drift-wave turbulence beyond the quasilinear approximation. J. Plasma Phys. 85, 905850101.CrossRefGoogle Scholar
Ruiz, D. E., Parker, J. B., Shi, E. L. & Dodin, I. Y. 2016 Zonal-flow dynamics from a phase-space perspective. Phys. Plasmas 23, 122304.CrossRefGoogle Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310.CrossRefGoogle Scholar
Srinivasan, K. & Young, W. R. 2012 Zonostrophic instability. J. Atmos. Sci. 69, 1633.CrossRefGoogle Scholar
St-Onge, D. A. 2017 On non-local energy transfer via zonal flow in the Dimits shift. J. Plasma Phys. 83, 905830504.CrossRefGoogle Scholar
Strintzi, D. & Jenko, F. 2007 On the relation between secondary and modulational instabilities. Phys. Plasmas 14, 042305.CrossRefGoogle Scholar
Sugama, H. & Horton, W. 1997 Transport processes and entropy production in toroidally rotating plasmas with electrostatic turbulence. Phys. Plasmas 4, 405.CrossRefGoogle Scholar
Sugama, H. & Horton, W. 1998 Nonlinear electromagnetic gyrokinetic equation for plasmas with large mean flows. Phys. Plasmas 5, 2560.CrossRefGoogle Scholar
Sugama, H., Okamoto, M., Horton, W. & Wakatani, M. 1996 Transport processes and entropy production in toroidal plasmas with gyrokinetic electromagnetic turbulence. Phys. Plasmas 3, 2379.CrossRefGoogle Scholar
Terry, P. W. & Horton, W. 1983 Drift wave turbulence in a low-order k space. Phys. Fluids 26, 106.CrossRefGoogle Scholar
Vallis, G. K. 2017 Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation, 2nd edn. CUP.CrossRefGoogle Scholar
Villard, L., Angelino, P., Bottino, A., Brunner, S., Jolliet, S., McMillan, B. F., Tran, T. M. & Vernay, T. 2013 Global gyrokinetic ion temperature gradient turbulence simulations of ITER. Plasma Phys. Control. Fusion 55, 074017.CrossRefGoogle Scholar
Villard, L., McMillan, B. F., Sauter, O., Hariri, F., Dominski, J., Merlo, G., Brunner, S. & Tran, T. M. 2014 Turbulence and zonal flow structures in the core and L-mode pedestal of tokamak plasmas. J. Phys.: Conf. Ser. 561, 012022.Google Scholar
Waltz, R. E. 1988 Three-dimensional global numerical simulation of ion temperature gradient mode turbulence. Phys. Fluids 31, 1962.CrossRefGoogle Scholar
Waltz, R. E., Dewar, R. L. & Garbet, X. 1998 Theory and simulation of rotational shear stabilization of turbulence. Phys. Plasmas 5, 1784.CrossRefGoogle Scholar
Waltz, R. E., Kerbel, G. D. & Milovich, J. 1994 Toroidal gyro-Landau fluid model turbulence simulations in a nonlinear ballooning mode representation with radial modes. Phys. Plasmas 1, 2229.CrossRefGoogle Scholar
van Wyk, F., Highcock, E. G., Field, A. R., Roach, C. M., Schekochihin, A. A., Parra, F. I. & Dorland, W. 2017 Ion-scale turbulence in MAST: anomalous transport, subcritical transitions, and comparison to BES measurements. Plasma Phys. Control. Fusion 59, 114003.CrossRefGoogle Scholar
van Wyk, F., Highcock, E. G., Schekochihin, A. A., Roach, C. M., Field, A. R. & Dorland, W. 2016 Transition to subcritical turbulence in a tokamak plasma. J. Plasma Phys. 82 (6), 905820609.CrossRefGoogle Scholar
Zhou, Y., Zhu, H. & Dodin, I. Y. 2019 Formation of solitary zonal structures via the modulational instability of drift waves. Plasma Phys. Control. Fusion 61, 075003.CrossRefGoogle Scholar
Zhou, Y., Zhu, H. & Dodin, I. Y. 2020 Solitary zonal structures in subcritical drift waves: a minimum model. Plasma Phys. Control. Fusion 62, 045021.CrossRefGoogle Scholar
Zhu, H., Zhou, Y. & Dodin, I. Y. 2018 a On the Rayleigh–Kuo criterion for the tertiary instability of zonal flows. Phys. Plasmas 25, 082121.CrossRefGoogle Scholar
Zhu, H., Zhou, Y. & Dodin, I. Y. 2018 b On the structure of the drifton phase space and its relation to the Rayleigh–Kuo criterion of the zonal-flow stability. Phys. Plasmas 25, 072121.CrossRefGoogle Scholar
Zhu, H., Zhou, Y. & Dodin, I. Y. 2019 Nonlinear saturation and oscillations of collisionless zonal flows. New J. Phys. 21, 063009.CrossRefGoogle Scholar
Zhu, H., Zhou, Y. & Dodin, I. Y. 2020 a Theory of the tertiary instability and the Dimits shift within a scalar model. J. Plasma Phys. 86 (4), 905860405.CrossRefGoogle Scholar
Zhu, H., Zhou, Y. & Dodin, I. Y. 2020 b Theory of the tertiary instability and the Dimits shift from reduced drift-wave models. Phys. Rev. Lett. 124, 055002.CrossRefGoogle ScholarPubMed
Supplementary material: File

Ivanov et al. Supplementary Material

Ivanov et al. Supplementary Material

Download Ivanov et al. Supplementary Material(File)
File 3.1 MB