Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-27T18:37:09.364Z Has data issue: false hasContentIssue false
  • English
  • Français

Weakly relativistic nonlinear orbit dynamics for intense ordinary-mode propagation near electron cyclotron resonance

Published online by Cambridge University Press:  13 March 2009

Ronald C. Davidson ,
Tser-Yuan Yang  and
Richard E. Aamodt
Ronald C. Davidson
Affiliation:
Science Applications International Corporation, McLean, Virginia 22102, U.S.A.
Tser-Yuan Yang
Affiliation:
Plasma Fusion Center, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, U.S.A.
Richard E. Aamodt
Affiliation:
Lodestar Research Corporation, Boulder, Colorado 80302, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

The nonlinear orbit equations are investigated analytically and numerically for a constant-amplitude electromagnetic wave (ωs, ks) with ordinary-mode polarization propagating perpendicular to a uniform magnetic field B0 êz. Relativisitic electron dynamics are essential in determining the maximum orbit excursion when the incident wave frequency ωs is near the nth harmonic of the electron cyclotron frequency Ωc. Coupled nonlinear equations are obtained for the slow evolution of the amplitude A(т) and phase ø(t) of the perpendicular orbit when ωs ≈ nΩc. The dynamical equations are reduced to quadrature and simplified analytically. At exact resonance (ωs = nΩc), if relativistic effects are (incorrectly) neglected, the maximum orbit excursion Amax approaches the unacceptably large value determined from the first (non-zero) solution to Jn(ns ΩsAmax) = 0, which totally invalidates the non-relativistic approximation. (Here ns Ωs = cks/Ωc.) As a contrasting illustrative example, for n = 1, ωs = Ωc and moderate pump strength, weak relativistic effects limit the maximum orbit excursion to the approximate value 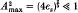, where єs = ns ωs (Vz/c) Vq/c ≪ 1, and Vq is the axial quiver velocity in the applied oscillatory field. Physically, relativistic effects produce a nonlinear frequency shift that dynamically ‘detunes’ the particle motion from exact cyclotron resonance, thereby limiting amplitude growth.

Type
Research Article
Information
Journal of Plasma Physics , Volume 41 , Issue 3 , June 1989 , pp. 405 - 426
Copyright
Copyright © Cambridge University Press 1989

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arnold, V. I. 1978 Mathematical Methods of Classical Mechanics. Springer.CrossRefGoogle Scholar
Bethe, H. A. & Rose, M. E. 1937 Phys. Rev. 52, 1254.CrossRefGoogle Scholar
Carter, M. D., Callen, J. D., Batchelor, D. B. & Goldfinger, R. C. 1986 Phys. Fluids, 29, 100.CrossRefGoogle Scholar
Chernikov, A. A., Sagdeev, R. Z., Usikov, D. A., Zakharov, M. Yu., Zaslavsky, G. M. 1987 Nature 326, 559.CrossRefGoogle Scholar
Davidson, R. C. 1987 Phys. Lett. 126A, 21.CrossRefGoogle Scholar
Hafizi, B. & Aamodt, R. E. 1987 Phys. Fluids, 30, 3059.CrossRefGoogle Scholar
Kreischer, K. E. & Temkin, R. J. 1987 Phys. Rev. Lett. 59, 547.CrossRefGoogle Scholar
McMillan, E. M. 1945 Phys. Rev. 68, 143.CrossRefGoogle Scholar
Nevins, W. M., Rognlien, T. D. & Cohen, B. I. 1987 Phys. Rev. Lett. 59, 60.CrossRefGoogle Scholar
Orzechowski, T. J., Anderson, B. R., Clark, J. C., Fawley, W. M., Paul, A. C., Prosnitz, D., Scharlemann, E. T., Yarema, S. M., Hopkins, D. B., Sessler, A. M. & Wurtele, J. S. 1986 Phys. Rev. Lett. 57, 2172.CrossRefGoogle Scholar
Suvorov, E. V. & Tokman, M. D. 1983 Plasma Phys. 25, 723.CrossRefGoogle Scholar