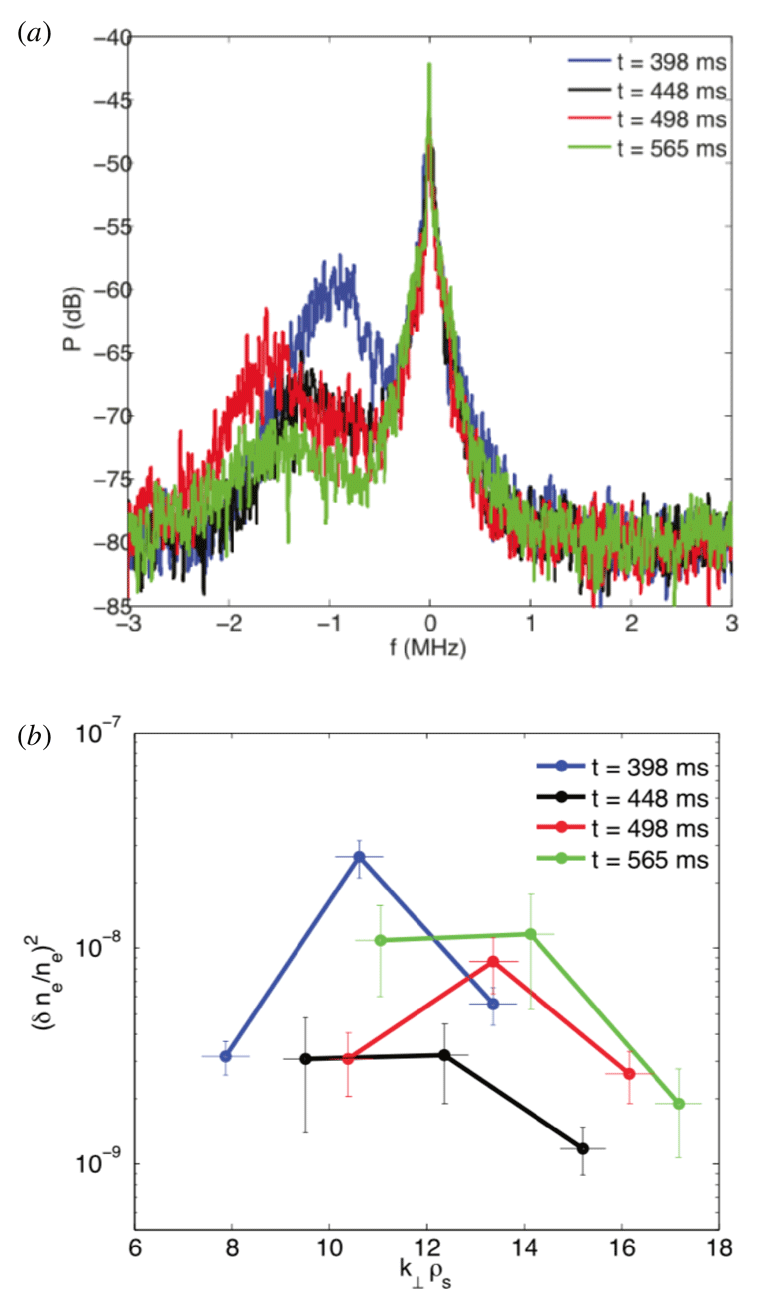
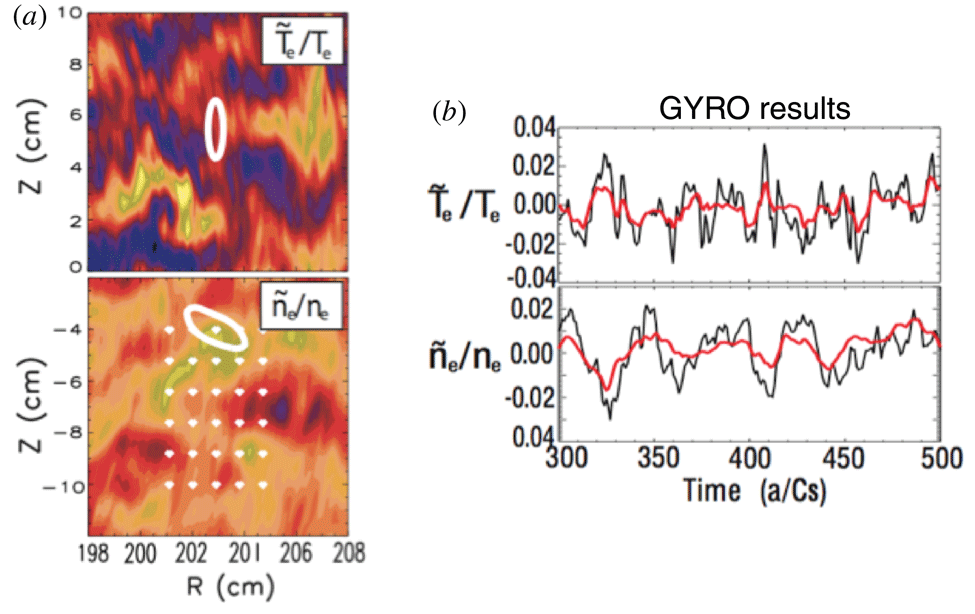
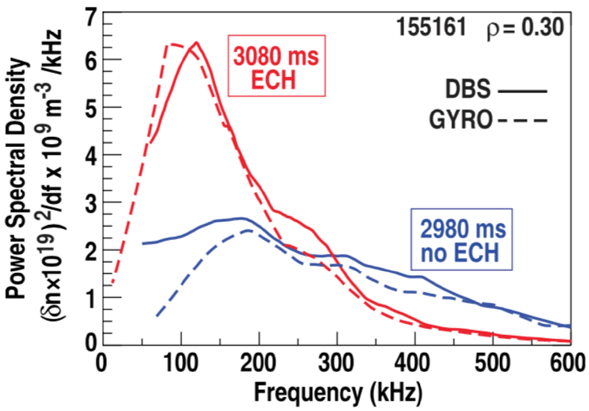
1 Introduction
Comparing gyrokinetic simulation results to experimental results via a rigorous methodology (Terry et al.
Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008; Greenwald Reference Greenwald2010) forms the area known as gyrokinetic validation within the fusion energy research field. The drift-wave turbulence observed in the core of fusion plasmas is well described by the nonlinear gyrokinetic equations coupled to Maxwell’s equations (Brizard & Hahm Reference Brizard and Hahm2007; Krommes Reference Krommes2010); nonlinear gyrokinetic theory is encapsulated in numerical gyrokinetic codes (Garbet Reference Garbet2010). The physics of drift-wave turbulence (Horton Reference Horton1999; Weiland Reference Weiland1999) in tokamak and stellarator plasmas has been extensively developed for many years. This effort is motivated by the desire to more accurately describe the higher than observed levels of cross-field heat and particle transport that occur in fusion plasmas. In the core region of fusion plasmas,
![]() $0.0<r/a<0.9$
, where
$0.0<r/a<0.9$
, where
![]() $r$
is the minor radius and
$r$
is the minor radius and
![]() $a$
is the plasma radius, the drift-wave instabilities and associated low frequency turbulence (with
$a$
is the plasma radius, the drift-wave instabilities and associated low frequency turbulence (with
![]() $\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}_{\text{ci}}$
), have small amplitudes with respect to the background densities and temperatures (e.g.
$\unicode[STIX]{x1D714}\ll \unicode[STIX]{x1D6FA}_{\text{ci}}$
), have small amplitudes with respect to the background densities and temperatures (e.g.
![]() ${\tilde{n}}/n\sim 1\,\%$
), and correlation lengths in the range of
${\tilde{n}}/n\sim 1\,\%$
), and correlation lengths in the range of
![]() ${\sim}0.1{-}10\unicode[STIX]{x1D70C}_{\text{s}}$
. Here
${\sim}0.1{-}10\unicode[STIX]{x1D70C}_{\text{s}}$
. Here
![]() $\unicode[STIX]{x1D6FA}_{\text{ci}}$
is the ion cyclotron frequency and
$\unicode[STIX]{x1D6FA}_{\text{ci}}$
is the ion cyclotron frequency and
![]() $\unicode[STIX]{x1D70C}_{\text{s}}$
is the ion sound gyroradius. Drift-wave instabilities are in general electromagnetic and occur at multiple scales, spanning a range of normalized wavenumbers
$\unicode[STIX]{x1D70C}_{\text{s}}$
is the ion sound gyroradius. Drift-wave instabilities are in general electromagnetic and occur at multiple scales, spanning a range of normalized wavenumbers
![]() $0<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<60$
, where
$0<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<60$
, where
![]() $k_{\unicode[STIX]{x1D703}}$
is the poloidal wavenumber of the fluctuations. The drift-wave turbulence described by nonlinear gyrokinetic theory leads to particle fluxes
$k_{\unicode[STIX]{x1D703}}$
is the poloidal wavenumber of the fluctuations. The drift-wave turbulence described by nonlinear gyrokinetic theory leads to particle fluxes
![]() $\unicode[STIX]{x1D6E4}_{\text{j}}=\langle {\tilde{n}}_{\text{j}}\tilde{v}E_{\text{r}}\rangle +n_{\text{j}}\langle \tilde{v}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B$
and energy fluxes
$\unicode[STIX]{x1D6E4}_{\text{j}}=\langle {\tilde{n}}_{\text{j}}\tilde{v}E_{\text{r}}\rangle +n_{\text{j}}\langle \tilde{v}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B$
and energy fluxes
![]() $Q_{\text{j}}=3/2\langle \tilde{p}_{\text{j}}\tilde{v}E_{\text{r}}\rangle +\langle \tilde{q}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B+5/2p_{\text{j}}\langle \tilde{v}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B$
, where subscript
$Q_{\text{j}}=3/2\langle \tilde{p}_{\text{j}}\tilde{v}E_{\text{r}}\rangle +\langle \tilde{q}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B+5/2p_{\text{j}}\langle \tilde{v}_{\text{j}\Vert }\tilde{B}_{\text{r}}\rangle /B$
, where subscript
![]() $\text{j}$
denotes the species (electrons or ions). The turbulent fluxes depend on the amplitude of fluctuations of the density
$\text{j}$
denotes the species (electrons or ions). The turbulent fluxes depend on the amplitude of fluctuations of the density
![]() ${\tilde{n}}$
, pressure
${\tilde{n}}$
, pressure
![]() $\tilde{p}$
, the parallel heat flux
$\tilde{p}$
, the parallel heat flux
![]() $\tilde{q}_{\Vert }$
, parallel velocities
$\tilde{q}_{\Vert }$
, parallel velocities
![]() $\tilde{v}_{\Vert }$
, electric field
$\tilde{v}_{\Vert }$
, electric field
![]() $\tilde{E}_{\text{r}}$
and magnetic field
$\tilde{E}_{\text{r}}$
and magnetic field
![]() $\tilde{B}_{\text{r}}$
. The fluxes also depend on the mean of the relative phases between the different fluctuations. The brackets denote ensemble averages of fluctuating quantities (Conway Reference Conway2008).
$\tilde{B}_{\text{r}}$
. The fluxes also depend on the mean of the relative phases between the different fluctuations. The brackets denote ensemble averages of fluctuating quantities (Conway Reference Conway2008).
The complex interplay among electromagnetic, multi-scale drift-wave turbulence and the background equilibrium flows (
![]() $E\times B$
shear) and self-generated flows (zonal flows and geodesic acoustic modes) in fusion plasmas forms a ‘standard’ turbulent-transport paradigm. This standard paradigm of turbulent-transport is part of the physics basis for ITER (Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Tujita2007). Over the last two decades, advances in numerical techniques have allowed for the development of high-fidelity gyrokinetic turbulence simulation codes (such as GENE (Jenko et al.
Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al.
Reference Görler, Lapillone, Brunner, Dannert, Jenko, Merz and Told2011) and GYRO (Candy & Waltz Reference Candy and Waltz2003a
) and many others) that are appropriate for direct and quantitative comparison with experiment. Gyrokinetic validation is used to test and extend the standard turbulent-transport paradigm as it is implemented in such codes in order to develop a deeper understanding of plasma turbulence and to advance predictive capabilities for fusion energy development.
$E\times B$
shear) and self-generated flows (zonal flows and geodesic acoustic modes) in fusion plasmas forms a ‘standard’ turbulent-transport paradigm. This standard paradigm of turbulent-transport is part of the physics basis for ITER (Doyle Reference Doyle, Houlberg, Kamada, Mukhovatov, Osborne, Polevoi, Bateman, Connor, Cordey and Tujita2007). Over the last two decades, advances in numerical techniques have allowed for the development of high-fidelity gyrokinetic turbulence simulation codes (such as GENE (Jenko et al.
Reference Jenko, Dorland, Kotschenreuther and Rogers2000; Görler et al.
Reference Görler, Lapillone, Brunner, Dannert, Jenko, Merz and Told2011) and GYRO (Candy & Waltz Reference Candy and Waltz2003a
) and many others) that are appropriate for direct and quantitative comparison with experiment. Gyrokinetic validation is used to test and extend the standard turbulent-transport paradigm as it is implemented in such codes in order to develop a deeper understanding of plasma turbulence and to advance predictive capabilities for fusion energy development.
General validation approaches in fusion energy research has been described in review articles (Terry et al. Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008; Greenwald Reference Greenwald2010). Validation of gyrokinetic codes specifically using validation metrics has also been reviewed in depth (Holland Reference Holland2016). This tutorial is intended to provide readers with a working knowledge of experimental steps necessary to compare nonlinear gyrokinetic codes with measurements of turbulence in tokamaks and stellarators. This tutorial provides descriptions of the experimental data used as input to gyrokinetic codes, as well discussion of the different turbulence parameters that can be measured in the core of fusion plasmas. The philosophy and workflow for comparing these measurements to nonlinear gyrokinetic simulation results is described.
This tutorial will focus primarily on using gradient-driven, local
![]() $\unicode[STIX]{x2202}f$
simulations for comparisons with measured turbulence. Local, gradient-driven
$\unicode[STIX]{x2202}f$
simulations for comparisons with measured turbulence. Local, gradient-driven
![]() $\unicode[STIX]{x2202}f$
gyrokinetic simulations have been used most extensively to date for comparisons with turbulence measurements. Published methodologies and best practices for gyrokinetic validation have discussed benefits of local, gradient-driven simulations for comparisons with experiment (Holland Reference Holland2016).
$\unicode[STIX]{x2202}f$
gyrokinetic simulations have been used most extensively to date for comparisons with turbulence measurements. Published methodologies and best practices for gyrokinetic validation have discussed benefits of local, gradient-driven simulations for comparisons with experiment (Holland Reference Holland2016).
In the
![]() $\unicode[STIX]{x2202}f$
formulation, a separation between turbulent scales and equilibrium profile scales is assumed, which is found to be a good assumption in the core plasma of medium-scale fusion devices (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammet and Jenko2010; Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013), when there is a sufficiently small ratio of ion Larmor radius to plasma minor radius, or
$\unicode[STIX]{x2202}f$
formulation, a separation between turbulent scales and equilibrium profile scales is assumed, which is found to be a good assumption in the core plasma of medium-scale fusion devices (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammet and Jenko2010; Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013), when there is a sufficiently small ratio of ion Larmor radius to plasma minor radius, or
![]() $\unicode[STIX]{x1D70C}^{\ast }$
. More details of the assumptions used in the
$\unicode[STIX]{x1D70C}^{\ast }$
. More details of the assumptions used in the
![]() $\unicode[STIX]{x2202}f$
formulation used in gyrokinetic codes is described in Garbet (Reference Garbet2010), and that article also provides a clear discussion of the effects of geometry, and benefits of both local models and global models. Because
$\unicode[STIX]{x2202}f$
formulation used in gyrokinetic codes is described in Garbet (Reference Garbet2010), and that article also provides a clear discussion of the effects of geometry, and benefits of both local models and global models. Because
![]() $\unicode[STIX]{x2202}f$
codes exploit the large scale separation between the spatiotemporal scales of the turbulence and the background pressure profiles, they can only model the effect the pressure profiles have on the turbulence, they do not model how the turbulence affects the evolution of the background profiles. In contrast, in a full-
$\unicode[STIX]{x2202}f$
codes exploit the large scale separation between the spatiotemporal scales of the turbulence and the background pressure profiles, they can only model the effect the pressure profiles have on the turbulence, they do not model how the turbulence affects the evolution of the background profiles. In contrast, in a full-
![]() $f$
global gyrokinetic code, the equilibrium and fluctuations are solved for self-consistently, assuming no scale separation (Garbet Reference Garbet2010). It is important to note that some
$f$
global gyrokinetic code, the equilibrium and fluctuations are solved for self-consistently, assuming no scale separation (Garbet Reference Garbet2010). It is important to note that some
![]() $\unicode[STIX]{x2202}f$
codes, like GYRO and GENE, can be run both locally and globally (Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013). Performing a ‘global run’ with the
$\unicode[STIX]{x2202}f$
codes, like GYRO and GENE, can be run both locally and globally (Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013). Performing a ‘global run’ with the
![]() $\unicode[STIX]{x2202}f$
codes typically refers to how the boundary conditions are treated in the simulation domain and whether the background profiles are allowed to vary spatially in the domain. This would be in contrast to a fully global treatment, where the background profiles evolved in time. Good agreement is found between the local and global simulations for both GENE and GYRO (Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013), when
$\unicode[STIX]{x2202}f$
codes typically refers to how the boundary conditions are treated in the simulation domain and whether the background profiles are allowed to vary spatially in the domain. This would be in contrast to a fully global treatment, where the background profiles evolved in time. Good agreement is found between the local and global simulations for both GENE and GYRO (Holland et al.
Reference Holland, Schmitz, Rhodes, Peebles, Hillesheim, Wang, Zeng, Doyle, Smith and Prater2011; Jenko et al.
Reference Jenko, Told, Görler, Citrin, Bañón Navarro, Bourdelle, Brunner, Conway, Dannert and Doerk2013), when
![]() $\unicode[STIX]{x1D70C}^{\ast }$
is sufficiently small in the core region of medium-size to large-size fusion plasmas.
$\unicode[STIX]{x1D70C}^{\ast }$
is sufficiently small in the core region of medium-size to large-size fusion plasmas.
This tutorial is limited in that it does not attempt to review the entirety of physics results obtained from gyrokinetic validation studies in the literature. This tutorial is intended to be code and model agnostic; however, as mentioned earlier, the majority of practical examples are drawn from experience with gradient-driven simulations, rather than flux-driven simulations (Garbet Reference Garbet2010); though the latter are discussed. In addition, the details of numerical methods used in gyrokinetic codes, such as how collisions,
![]() $E\times B$
shear or boundary conditions are implemented, are outside the scope of this paper. These details are of course highly relevant for both model validation and verification. Keep in mind that a necessary condition for validation is to use a verified code (Greenwald Reference Greenwald2010); and validation and verification are not the same. For gyrokinetic transport models, verification is performed mostly via code-to-code comparisons, or benchmarking exercises (Bravenec et al.
Reference Bravenec, Chen, Candy, Wan and Parker2013; Merlo et al.
Reference Merlo, Dominski, Bhattacharjee, Chang, Jenko, Ku, Lanti and Parker2018; Mikkelsen et al.
Reference Mikkelsen, Howard, White and Creely2018) and is not covered in this tutorial. On the experimental side, a much broader review of data analysis and data validation in fusion plasmas is presented by Arshad et al. (Reference Arshad, Cordey, McDonald, Farthing, Joffrin, von Hellermann, Roach and Svensson2008) and a review of turbulence measurements and data analysis techniques is found in Tynan, Fujisawa & McKee (Reference Tynan, Fujisawa and McKee2009).
$E\times B$
shear or boundary conditions are implemented, are outside the scope of this paper. These details are of course highly relevant for both model validation and verification. Keep in mind that a necessary condition for validation is to use a verified code (Greenwald Reference Greenwald2010); and validation and verification are not the same. For gyrokinetic transport models, verification is performed mostly via code-to-code comparisons, or benchmarking exercises (Bravenec et al.
Reference Bravenec, Chen, Candy, Wan and Parker2013; Merlo et al.
Reference Merlo, Dominski, Bhattacharjee, Chang, Jenko, Ku, Lanti and Parker2018; Mikkelsen et al.
Reference Mikkelsen, Howard, White and Creely2018) and is not covered in this tutorial. On the experimental side, a much broader review of data analysis and data validation in fusion plasmas is presented by Arshad et al. (Reference Arshad, Cordey, McDonald, Farthing, Joffrin, von Hellermann, Roach and Svensson2008) and a review of turbulence measurements and data analysis techniques is found in Tynan, Fujisawa & McKee (Reference Tynan, Fujisawa and McKee2009).
This paper is organized as follows: § 2 presents a brief history of gyrokinetic transport model validation and best practices, focusing on the use of fluctuation measurements. This section discusses challenges particular to validation of gyrokinetic transport models, and provides a practical workflow-level view of validation from an experimental perspective. Section 3 describes the analysis steps required for preparing experimental data for comparisons with gyrokinetic codes. Section 4 provides a survey of several common turbulence diagnostics that have been used in gyrokinetic validation studies over the past decade, describing their fundamental operational principles and basic data analysis techniques. Section 5 presents an overview of synthetic diagnostics, which are needed to quantitatively compare turbulence measurements to gyrokinetic simulations. Section 6 presents several open questions in validation and examples of work at the frontiers of the field, with § 7 concluding with a discussion and outlook for the field.
2 Gyrokinetic transport model validation and best practices
2.1 Brief history of gyrokinetic model validation
There have been many milestones in gyrokinetic transport model validation in the last two decades. Here, only a few are highlighted as they pertain to defining the challenges and actionable aspects of validation using turbulence measurements. One important result is from Lin et al. (Reference Lin, Hahm, Lee, Tang and White1998), which demonstrated that the interaction between zonal flows (Diamond Reference Diamond2005) and turbulence is a nonlinear saturation mechanism that has important implications for reducing turbulent amplitudes and associated heat flux. A second milestone of interest was that of Candy & Waltz (Reference Candy and Waltz2003b
), which demonstrated that nonlinear gyrokinetic codes could match both the experimental ion and electron transport levels within error bars, when sheared equilibrium
![]() $E\times B$
shear rotation (Burrell Reference Burrell1998) effects were included in the model. Around the same time, radial correlation lengths obtained using reflectometer measurements were first compared with gyrokinetic simulations (Rhodes et al.
Reference Rhodes, Leboeuf, Sydora, Groebner, Doyle, McKee, Peebles, Rittig, Zeng and Wang2002). The results showed that self-generated zonal flows were required to reduce the simulated correlation length of the turbulence, bringing it into agreement with the experimental values. Another paper that same year described comparisons between gyrokinetic simulations and experimental ion and electron heat fluxes, and also turbulent fluctuation levels measured with a beam-emission spectroscopy (BES) diagnostic (Ross & Dorland Reference Ross and Dorland2002). The results showed that including
$E\times B$
shear rotation (Burrell Reference Burrell1998) effects were included in the model. Around the same time, radial correlation lengths obtained using reflectometer measurements were first compared with gyrokinetic simulations (Rhodes et al.
Reference Rhodes, Leboeuf, Sydora, Groebner, Doyle, McKee, Peebles, Rittig, Zeng and Wang2002). The results showed that self-generated zonal flows were required to reduce the simulated correlation length of the turbulence, bringing it into agreement with the experimental values. Another paper that same year described comparisons between gyrokinetic simulations and experimental ion and electron heat fluxes, and also turbulent fluctuation levels measured with a beam-emission spectroscopy (BES) diagnostic (Ross & Dorland Reference Ross and Dorland2002). The results showed that including
![]() $E\times B$
shear was important to reduce the heat flux and turbulent levels nearer the experiment, but it was not possible to match the experimental values within error bars.
$E\times B$
shear was important to reduce the heat flux and turbulent levels nearer the experiment, but it was not possible to match the experimental values within error bars.
The specifics of the agreement and disagreement in these ‘first validation papers’ (Rhodes et al. Reference Rhodes, Leboeuf, Sydora, Groebner, Doyle, McKee, Peebles, Rittig, Zeng and Wang2002; Ross & Dorland Reference Ross and Dorland2002) are not what make these papers of interest in this tutorial. Instead, it is because the work includes many of the modern ‘best practices’ for validation, later described in review papers (Terry et al. Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008; Greenwald Reference Greenwald2010; Holland Reference Holland2016). Key concepts and best practices in validation include qualification of the domain of model applicability and limitations, identifying uncertainties in the model and the experiment, recognizing known deficiencies or excluded physics in the model, sensitivity analysis and use of the primacy hierarchy and validation metrics (Terry et al. Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008; Holland Reference Holland2016). The papers (Rhodes et al. Reference Rhodes, Leboeuf, Sydora, Groebner, Doyle, McKee, Peebles, Rittig, Zeng and Wang2002; Ross & Dorland Reference Ross and Dorland2002), were among the first to systematically scan code inputs within experimental error bars to test model sensitivity. These papers also used many validation observables in a primacy hierarchy (though did not call it by this name) to compare not just to heat fluxes inferred from power balance, but also measured turbulence, to the simulations. These papers also featured the description and use of multiple transport models. Within a gyrokinetic code, the user can turn on and off different physics effects within the same code. This allows the validation concepts of qualification and deficiency of models to be addressed. It is more appropriate to discuss validation of transport models (which can be run using the same code or different codes), rather than validation of a transport code.

Figure 1. Validation of a model is a process. After a dedicated experiment is run, the experimental measurements of turbulence and transport (validation observables) are compared with outputs from the codes. Points of agreement and disagreement are assessed (ideally, quantified using validation metrics), and new models or and/or measurements are developed, and the cycle, or parts of it, is repeated.
For validation of the gyrokinetic turbulent-transport model, numerical codes must be used, which adds to the complexity of making these comparisons. Figure 1 shows an abstract diagram of the validation process, which is iterative, and ideally combines experimental and simulation planning in parallel. Perhaps the most important guiding principle is that the goal of a successful validation study should not be to achieve agreement between experiment and simulation. The purpose of a successful validation study is to understand the reasons for agreement or disagreement between the experiment and the model. Robust agreements and disagreements that can be understood in terms of physics in the model or measurement limitations etc., will lead to progress in development of new models and experiments, and ultimately, to deeper understanding of turbulent transport in fusion plasmas. Serendipitous agreements and accidental disagreements do not aid scientific progress. Reporting robust disagreement is just as important as reporting robust agreement. While not an exhaustive list, the following selected papers from the last decade contain several good examples of the ‘best practices’ in validation put to use for comparisons between simulation and experimental ion and electron heat transport, impurity transport and a variety of turbulence measurements in L-mode, I-mode (Whyte et al. Reference Whyte, Hubbard, Hughes, Lipschultz, Rice, Marmar, Greenwald, Cziegler, Dominguez and Golfinopoulos2010) and H-mode plasmas in tokamaks: White et al. Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gurcan and Heuraux2009; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; White et al. 2010; Rhodes et al. Reference Rhodes, Holland, Smith, White, Burrell, Candy, Deboo, Doyle, Hillesheim and Kinsey2011; Holland et al. Reference Holland, Petty, Schmitz, Burrell, McKee, Rhodes and Candy2012; Howard et al. Reference Howard, Greenwald, Mikkelsen, Reinke, White, Ernst, Podpaly and Candy2012; Told et al. Reference Told, Jenko, Görler, Casson and Fable2013; Citrin et al. Reference Citrin, Jeko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij and Johnson2014; Field et al. Reference Field, Dunai, Ghim, Hill, McMillan, Roach, Saarelma, Schekochihin and Zoletnik2014; Görler et al. Reference Görler, White, Told, Jenko, Holland and Rhodes2014; Sung et al. Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016; Creely et al. Reference Creely, Howard, Rodriguez-Fernandez, Cao, Hubbard, Hughes, Rice, White, Candy and Staebler2017; van Wyk et al. Reference van Wyk, Highcock, Field, Roach, Schekochihin, Parra and Dorland2017; Freethy et al. Reference Freethy, Görler, Creely, Conway, Happel and White2018; Howard et al. Reference Howard, Holland, White, Greenwald, Rodriguez-Fernandez, Candy and Creely2018.
2.2 Designing gyrokinetic model validation experiments
Dedicated validation experiments provide the best opportunities for rigorous comparison between experiment and theory, as encapsulated in a model. Carrying out a carefully controlled validation experiment in fusion plasmas and subsequent comparisons with gyrokinetic codes presents several challenges, a few of which are described below.
First, when planning an experiment to study drift-wave turbulence and transport in fusion plasmas, one will seek to isolate a particular physical effect in the model. For example, the drift-wave turbulence is highly sensitive to the primary driving gradient(s). Both the linear instabilities, or modes, and the turbulence associated with the nonlinearly saturated state, can be classified according to the dominant driving mechanism. Three primary instabilities of interest in the core plasma are the ion temperature gradient (ITG) mode, the electron temperature gradient (ETG) and the trapped electron mode (TEM). ITG modes are long-wavelength ion-scale (
![]() $k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<1$
) instabilities that are driven by the ion temperature gradient. ETG modes are short-wavelength electron-scale (
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<1$
) instabilities that are driven by the ion temperature gradient. ETG modes are short-wavelength electron-scale (
![]() $k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}>1$
) instabilities that are driven by the electron temperature gradient. TEMs can span both long and short wavelengths, and are driven by electron temperature and density gradients. ITG, TEM and ETG modes can exist electrostatically, and persist when electromagnetic effects are included. A fourth type, the microtearing modes (MTMs), are long-wavelength ion-scale electromagnetic instabilities that are excited at high plasma beta and are driven by electron temperature gradients. The kinetic ballooning mode (KBM) can also play a role at high beta (Ishizawa et al.
Reference Ishizawa, Maeyama, Watanabe, Sugama and Nakajima2013) and the resistive ballooning mode (RBM) may become relevant in the edge region, especially in L-mode plasmas (Rogers, Drake & Zeiler Reference Rogers, Drake and Zeiler1998). It is always good practice to perform a linear stability analysis survey in the plasmas of interest prior to nonlinear simulation, to help guide the set-up and execution of the nonlinear runs. In addition to the primary driving gradients, drift-wave turbulence is also very sensitive to the shape of the plasma, the magnetic shear, the
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}>1$
) instabilities that are driven by the electron temperature gradient. TEMs can span both long and short wavelengths, and are driven by electron temperature and density gradients. ITG, TEM and ETG modes can exist electrostatically, and persist when electromagnetic effects are included. A fourth type, the microtearing modes (MTMs), are long-wavelength ion-scale electromagnetic instabilities that are excited at high plasma beta and are driven by electron temperature gradients. The kinetic ballooning mode (KBM) can also play a role at high beta (Ishizawa et al.
Reference Ishizawa, Maeyama, Watanabe, Sugama and Nakajima2013) and the resistive ballooning mode (RBM) may become relevant in the edge region, especially in L-mode plasmas (Rogers, Drake & Zeiler Reference Rogers, Drake and Zeiler1998). It is always good practice to perform a linear stability analysis survey in the plasmas of interest prior to nonlinear simulation, to help guide the set-up and execution of the nonlinear runs. In addition to the primary driving gradients, drift-wave turbulence is also very sensitive to the shape of the plasma, the magnetic shear, the
![]() $E\times B$
shear, etc. These effects have been explored using many simulations run over very large input parameter ranges, with examples shown in Kinsey, Waltz & Candy (Reference Kinsey, Waltz and Candy2006, Reference Kinsey, Waltz and Candy2007). These parameters can be controlled in tokamak and stellarator plasmas to some extent, but typically only over a limited range compared to simulation. And unlike in simulation, isolating the effect of one parameter is difficult (if not impossible) in the experiment.
$E\times B$
shear, etc. These effects have been explored using many simulations run over very large input parameter ranges, with examples shown in Kinsey, Waltz & Candy (Reference Kinsey, Waltz and Candy2006, Reference Kinsey, Waltz and Candy2007). These parameters can be controlled in tokamak and stellarator plasmas to some extent, but typically only over a limited range compared to simulation. And unlike in simulation, isolating the effect of one parameter is difficult (if not impossible) in the experiment.
Second, it is of interest to design dedicated validation experiments that minimize the uncertainties and errors on the measurements that the codes are using as input. Minimizing the errors is essential because it is well known that the nonlinear gyrokinetic model can be hypersensitive to input parameters (Holland Reference Holland2016). For example, the error bar on an input parameter in a gradient-driven simulation, like the normalized logarithmic gradient of ion temperature,
![]() $a/L_{\text{Ti}}$
, may be 20 %. Within this range, the models can exhibit extreme sensitivity. This is because many of the modes exhibit a threshold in the gradient driving the instability: the mode is linearly stable below the threshold, or ‘critical gradient’, and unstable above. Nonlinearly, the saturated turbulence also exhibits a critical gradient, different from the linear value (Garbet Reference Garbet2010). Stiffness is defined in this paper the incremental change in flux for an incremental change in gradient above the critical gradient, which is a typical definition employed in gyrokinetic simulation studies (Citrin et al.
Reference Citrin, Jeko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij and Johnson2014). Other definitions of stiffness and experimental investigations are described in the following references (Garbet et al.
Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolfe2004; Ryter et al.
Reference Ryter, Camenen, DeBoo, Imbeaux, Mantica, Regnoli, Sozzi and Stroth2006; Mantica et al.
Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009; DeBoo et al.
Reference DeBoo, Petty, White, Burrell, Doyle, Hillesheim, Holland, McKee, Rhodes and Schmitz2012).
$a/L_{\text{Ti}}$
, may be 20 %. Within this range, the models can exhibit extreme sensitivity. This is because many of the modes exhibit a threshold in the gradient driving the instability: the mode is linearly stable below the threshold, or ‘critical gradient’, and unstable above. Nonlinearly, the saturated turbulence also exhibits a critical gradient, different from the linear value (Garbet Reference Garbet2010). Stiffness is defined in this paper the incremental change in flux for an incremental change in gradient above the critical gradient, which is a typical definition employed in gyrokinetic simulation studies (Citrin et al.
Reference Citrin, Jeko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij and Johnson2014). Other definitions of stiffness and experimental investigations are described in the following references (Garbet et al.
Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolfe2004; Ryter et al.
Reference Ryter, Camenen, DeBoo, Imbeaux, Mantica, Regnoli, Sozzi and Stroth2006; Mantica et al.
Reference Mantica, Strintzi, Tala, Giroud, Johnson, Leggate, Lerche, Loarer, Peeters and Salmi2009; DeBoo et al.
Reference DeBoo, Petty, White, Burrell, Doyle, Hillesheim, Holland, McKee, Rhodes and Schmitz2012).

Figure 2. Nonlinear GYRO calculated output of ion heat flux,
![]() $Q_{\text{i}}$
, and electron heat flux,
$Q_{\text{i}}$
, and electron heat flux,
![]() $Q_{\text{e}}$
, against the input values of
$Q_{\text{e}}$
, against the input values of
![]() $a/L_{\text{Ti}}$
, showing critical gradient behaviour and ‘stiff’ response in the flux-gradient curve, taken from figure 7 Howard et al. (Reference Howard, White, Reinke, Greenwald, Holland, Candy and Walk2013).
$a/L_{\text{Ti}}$
, showing critical gradient behaviour and ‘stiff’ response in the flux-gradient curve, taken from figure 7 Howard et al. (Reference Howard, White, Reinke, Greenwald, Holland, Candy and Walk2013).
In figure 2 nonlinear ion-scale gyrokinetic simulation output results at
![]() $r/a=0.5$
for two L-mode plasmas in C-Mod are shown. Details of the simulations can be found in Howard et al. (Reference Howard, White, Reinke, Greenwald, Holland, Candy and Walk2013). The calculated output ion heat flux is plotted versus code input
$r/a=0.5$
for two L-mode plasmas in C-Mod are shown. Details of the simulations can be found in Howard et al. (Reference Howard, White, Reinke, Greenwald, Holland, Candy and Walk2013). The calculated output ion heat flux is plotted versus code input
![]() $a/L_{\text{Ti}}$
. Below the critical gradient, there is no heat flux driven, and above the critical gradient, the heat flux can increase dramatically, a factor of 10 increase in the output heat flux for a 10 % change in the ion temperature gradient. These plasmas, like most experimental plasmas, are classified as being very ‘stiff’. Sensitivity of the model outputs to the input driving gradient magnifies any experimental uncertainty. In figure 2, the experimental error bars (
$a/L_{\text{Ti}}$
. Below the critical gradient, there is no heat flux driven, and above the critical gradient, the heat flux can increase dramatically, a factor of 10 increase in the output heat flux for a 10 % change in the ion temperature gradient. These plasmas, like most experimental plasmas, are classified as being very ‘stiff’. Sensitivity of the model outputs to the input driving gradient magnifies any experimental uncertainty. In figure 2, the experimental error bars (
![]() $\pm 1$
sigma on the experimental ion heat flux,
$\pm 1$
sigma on the experimental ion heat flux,
![]() $Q_{\text{i}}$
) are marked by the shaded box. The error on the experimental value
$Q_{\text{i}}$
) are marked by the shaded box. The error on the experimental value
![]() $a/L_{\text{Ti}}$
is
$a/L_{\text{Ti}}$
is
![]() $1\unicode[STIX]{x1D70E}=\pm 20\,\%$
. In this case the experimental gradients, within the measured error bars, bracket a range above and below the calculated nonlinear critical gradient. This makes simulation of experimental conditions quite challenging, and computationally much more expensive than simulations run with the strongly driven ITG dominant cyclone base case (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000), a common benchmarking case used to compare across codes. To address this hypersensitivity and the resulting uncertainties, developing rigorous validation metrics is essential (Holland Reference Holland2016).
$1\unicode[STIX]{x1D70E}=\pm 20\,\%$
. In this case the experimental gradients, within the measured error bars, bracket a range above and below the calculated nonlinear critical gradient. This makes simulation of experimental conditions quite challenging, and computationally much more expensive than simulations run with the strongly driven ITG dominant cyclone base case (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000), a common benchmarking case used to compare across codes. To address this hypersensitivity and the resulting uncertainties, developing rigorous validation metrics is essential (Holland Reference Holland2016).
Some practical things to keep in mind with normalized parameters like the normalized logarithmic gradient of ion temperature,
![]() $a/L_{\text{Ti}}$
. First, gyrokinetic equations generally use the assumption that the gyroradius,
$a/L_{\text{Ti}}$
. First, gyrokinetic equations generally use the assumption that the gyroradius,
![]() $\unicode[STIX]{x1D70C}$
, is much smaller than the equilibrium scale length,
$\unicode[STIX]{x1D70C}$
, is much smaller than the equilibrium scale length,
![]() $L$
, that is,
$L$
, that is,
![]() $\unicode[STIX]{x1D70C}/L\ll 1$
(Weiland Reference Weiland1999). The inverse scale length,
$\unicode[STIX]{x1D70C}/L\ll 1$
(Weiland Reference Weiland1999). The inverse scale length,
![]() $1/L$
, is the logarithmic gradient of the temperature (or density, etc.), and for a Maxwellian distribution, appears in the diamagnetic drift frequency when one derives the linear gyrokinetic equation (Antonsen & Lane Reference Antonsen and Lane1980; Weiland Reference Weiland1999). In the literature, one will find that inverse scale length,
$1/L$
, is the logarithmic gradient of the temperature (or density, etc.), and for a Maxwellian distribution, appears in the diamagnetic drift frequency when one derives the linear gyrokinetic equation (Antonsen & Lane Reference Antonsen and Lane1980; Weiland Reference Weiland1999). In the literature, one will find that inverse scale length,
![]() $1/L$
, is sometimes normalized by the plasma minor radius,
$1/L$
, is sometimes normalized by the plasma minor radius,
![]() $a$
, or by the machine major radius,
$a$
, or by the machine major radius,
![]() $R_{0}$
, or by the local value of the major radius,
$R_{0}$
, or by the local value of the major radius,
![]() $R$
; take care to identify which normalization the author is using.
$R$
; take care to identify which normalization the author is using.
Third, it is of interest to consider extreme cases motivated by theory, even though they cannot be tested directly. For example, in the cyclone base case (Dimits et al.
Reference Dimits, Bateman, Beer, Cohen, Dorland, Hammett, Kim, Kinsey, Kotschenreuther and Kritz2000), the plasma is dominated by strongly driven ITG turbulence. Plasmas with only ITG-type turbulence can be studied numerically by setting
![]() $a/L_{\text{Te}}=0$
, and similarly only TEM-type turbulence can be studied by setting
$a/L_{\text{Te}}=0$
, and similarly only TEM-type turbulence can be studied by setting
![]() $a/L_{\text{Ti}}=0$
in an ion-scale gyrokinetic simulation (Dannert & Jenko Reference Dannert and Jenko2005). It is not possible to create such a ‘pure mode’ state in experiments. Many experimental fusion plasmas will be ‘mixed mode’ over most of the core plasma, and when simulated, these plasmas are found to contain features of both types of turbulence (linear and nonlinear) within the range of experimental error bars considered for the gradient scale lengths, with one example being Sung et al. (Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016). This can make it difficult to isolate physical effects that lead to agreement or disagreement with experiment in the validation study. Therefore, it is of interest to try to design a plasma that features dominant TEM turbulence (or ITG turbulence) (White et al. 2010; White et al.
Reference White, Howard, Creely, Chilenski, Greenwald, Hubbard, Hughes, Marmar, Rice and Sierchio2015; Ernst et al.
Reference Ernst, Burrell, Guttenfelder, Rhodes, Dimits, Bravenec, Grierson, Holland, Lohr and Marinoni2016). Both linear and nonlinear gyrokinetic simulations can be used for predictive experimental design in such cases. The use of validation metrics can help discriminate between models to ultimately isolate physical effects (Holland Reference Holland2016).
$a/L_{\text{Ti}}=0$
in an ion-scale gyrokinetic simulation (Dannert & Jenko Reference Dannert and Jenko2005). It is not possible to create such a ‘pure mode’ state in experiments. Many experimental fusion plasmas will be ‘mixed mode’ over most of the core plasma, and when simulated, these plasmas are found to contain features of both types of turbulence (linear and nonlinear) within the range of experimental error bars considered for the gradient scale lengths, with one example being Sung et al. (Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016). This can make it difficult to isolate physical effects that lead to agreement or disagreement with experiment in the validation study. Therefore, it is of interest to try to design a plasma that features dominant TEM turbulence (or ITG turbulence) (White et al. 2010; White et al.
Reference White, Howard, Creely, Chilenski, Greenwald, Hubbard, Hughes, Marmar, Rice and Sierchio2015; Ernst et al.
Reference Ernst, Burrell, Guttenfelder, Rhodes, Dimits, Bravenec, Grierson, Holland, Lohr and Marinoni2016). Both linear and nonlinear gyrokinetic simulations can be used for predictive experimental design in such cases. The use of validation metrics can help discriminate between models to ultimately isolate physical effects (Holland Reference Holland2016).
Fourth, it is important to measure as many different turbulence and transport parameters as possible to better assess and ideally quantify the agreement between the model and experiment. This motivates the use of turbulence measurements (§ 4) and synthetic diagnostics (§ 5) for validation of nonlinear gyrokinetic codes. All the relevant physical quantities that can be measured or inferred (fluctuation levels, cross-phase angles, correlation lengths, heat fluxes, etc.) become the validation observables, and are organized into a ‘primacy hierarchy’ (Terry et al.
Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008; Greenwald Reference Greenwald2010). The primacy hierarchy addresses several challenges, and in particular, helps to avoid fortuitous agreement (or disagreement) and helps to discriminate between models, especially in the case when the models are hypersensitive to input parameters. For gyrokinetic transport model validation, fluctuation levels of electron density and temperature, and their respective power spectra, tend to be measured most directly in experiments, and so are at the highest level in the primacy hierarchy. Correlation lengths and cross-phase angles are at the second level, because they require processing of two turbulence measurements. If turbulent particle,
![]() $\unicode[STIX]{x1D6E4}_{\text{j}}$
, or heat flux,
$\unicode[STIX]{x1D6E4}_{\text{j}}$
, or heat flux,
![]() $Q_{\text{j}}$
, of species
$Q_{\text{j}}$
, of species
![]() $\text{j}$
were to be measured in the experiment using combinations of fluctuation data, then these would be at the third level. These measurements are extremely challenging to make in the core plasma
$\text{j}$
were to be measured in the experiment using combinations of fluctuation data, then these would be at the third level. These measurements are extremely challenging to make in the core plasma
![]() $(r/a<0.9)$
where the gyrokinetic model is most applicable. The inferred heat fluxes from power balance calculations would be classified as belonging at some very low level, because they are not measured directly. Defining a validation metric and applying it to the observables from experiments can be done in a variety of ways. One example from the TORPEX basic plasma experiments has been used to successfully discriminate between turbulence models (Ricci et al.
Reference Ricci, Theiler, Fasoli, Furno, Gustafson, Iraji and Loizu2011). The same metric has since been applied at ASDEX Upgrade to identify a nonlinear gyrokinetic simulation with the ‘best match’ to experiment, using inferred heat fluxes, electron temperature fluctuation levels, radial correlation lengths and the cross-phase angle between density and temperature fluctuations as the validation observables (Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018). It is important to note that the strength of the primacy hierarchy and validation metric in these examples is discriminating between models, rather than assessing a single model in isolation; hence, from a practical perspective, planning for a validation experiment in a fusion device also means planning for computing resources needed to perform runs of different models with a gyrokinetic code.
$(r/a<0.9)$
where the gyrokinetic model is most applicable. The inferred heat fluxes from power balance calculations would be classified as belonging at some very low level, because they are not measured directly. Defining a validation metric and applying it to the observables from experiments can be done in a variety of ways. One example from the TORPEX basic plasma experiments has been used to successfully discriminate between turbulence models (Ricci et al.
Reference Ricci, Theiler, Fasoli, Furno, Gustafson, Iraji and Loizu2011). The same metric has since been applied at ASDEX Upgrade to identify a nonlinear gyrokinetic simulation with the ‘best match’ to experiment, using inferred heat fluxes, electron temperature fluctuation levels, radial correlation lengths and the cross-phase angle between density and temperature fluctuations as the validation observables (Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018). It is important to note that the strength of the primacy hierarchy and validation metric in these examples is discriminating between models, rather than assessing a single model in isolation; hence, from a practical perspective, planning for a validation experiment in a fusion device also means planning for computing resources needed to perform runs of different models with a gyrokinetic code.
From the perspective of an experimental approach, or workflow, for validation of gyrokinetic transport models, several general recommendations can be made: run experiments to obtain the highest quality of data used as input to verified and well-documented power balance codes and gyrokinetic codes, measure at many levels of the primacy hierarchy, measure turbulence at multiple radial locations, make multi-field fluctuation measurements (e.g. both
![]() $\unicode[STIX]{x1D6FF}T_{\text{e}}$
and
$\unicode[STIX]{x1D6FF}T_{\text{e}}$
and
![]() $\unicode[STIX]{x1D6FF}n_{\text{e}}$
) when possible, take care with quantification of uncertainties on experimental parameters, apply synthetic diagnostics, plan to use computing resources for extensive sensitivity scans with the codes both before and after an experiment, and use validation metrics.
$\unicode[STIX]{x1D6FF}n_{\text{e}}$
) when possible, take care with quantification of uncertainties on experimental parameters, apply synthetic diagnostics, plan to use computing resources for extensive sensitivity scans with the codes both before and after an experiment, and use validation metrics.
2.3 Example validation workflow
Let us say that we wish to design an experiment to study how the turbulence and transport changes as the electron temperature gradients are varied. The profile changes will be actuated with electron cyclotron resonance heating (ECRH) power in an H-mode plasma. We want to use Doppler reflectometry (see § 4) to measure the turbulence at several radial locations at each power level in the ECRH scan. Depending on the details of the Doppler reflectometer system, it may take one discharge at each power level to obtain the desired data set, or multiple discharges. It may be possible to change the power level during a long discharge and complete the desired Doppler reflectometer data set in a single shot. But keep in mind that for many fluctuation diagnostics, long, steady phases of the discharge will yield the best turbulence data. Prior to the experiment, development of a reliable synthetic diagnostic for the turbulence measurements may require a separate, possibly extensive, modelling project.
In addition to gathering the turbulence data, it is essential to also gather all the profile data required for comparisons with simulation; and long steady periods in the discharge will help reduce uncertainties on the measured background profiles. Of course, this type of planning is done for any experiment, and is not unique to a dedicated validation experiment. What is unique to a validation experiment is the interweaving of simulation planning and experiment planning from the beginning. This helps to guarantee that the comparisons with gyrokinetic codes will lend themselves to application of a rigorous validation methodology.
Once the experiment is designed, plans can be made for the steps required in the workflow, which will require both experimental data analysis and preparatory scoping scans with the codes. An example workflow based on using a gradient-driven gyrokinetic code to compare with experimental fluctuation measurements is presented in this section. Use of different codes (like a flux-driven code) will require a different workflow, in which case certain steps may be omitted and new steps may be added, but the spirit of the process remains the same.
Step 1: Identify a target discharge where high quality Doppler reflectometry (DR) was obtained previously. Check that the plasma parameters are within the domain of the model applicability for the model to be tested.
Step 2: Check that the target discharge also allows for high quality equilibrium reconstruction, ion and electron profile measurements, density profile measurements, rotation measurements, current profile measurements, etc. If additional turbulence measurements can be obtained in the same discharge, include them in planning as well. Obtaining as many measurements as possible, the validation observables, is important for later application of a validation metric.
Step 3: Check that the target discharge will stay in H-mode during the heating power scan (e.g. you might decrease electron cyclotron resonance heating (ECRH) in 0.5 MW steps). Check that the DR (and any other fluctuation measurements) will still be able to make quality measurements in the radial region of interest during the ECRH scan.
Step 4: Set-up an input file for gyrokinetic simulations of the target discharge. Run linear gyrokinetic simulations on the target ‘base case’ (experimental inputs used with no changes) and perform sensitivity scans to understand what mode or modes are unstable in the radial regions of interest. This step is critical to identify the gyrokinetic model to use in the nonlinear gyrokinetic simulations in the next step (electromagnetic or electrostatic, ion-scale versus electron-scale turbulence, drift kinetic versus gyrokinetic species, impurities, etc.).
Step 5: If resources permit, run nonlinear simulations of the target plasma as well. Run wavenumber and/or radial resolution scans, box-size scans, etc. to develop an understanding of how to get a numerically robust result for these plasma conditions. Take special care to numerically resolve the linear instability identified from Step 4. Most actual experimental conditions live very close to marginal stability, and the simulations are much more challenging and computationally intensive to run compared to more theoretical cases like the cyclone base case. If resources permit, change the input gradients and other input parameters in a way that mimics how the actual plasma parameters might change during the ECRH scan. If resources permit, attempt to predict what changes would be seen in the turbulence data using a synthetic diagnostic (§ 5).
Step 6: Run the actual experiment and analyse the data. Iterate the data analysis steps (§§ 3.1–3.3) as needed to generate kinetic equilibrium reconstruction, smooth profile fits and well-constrained power balance calculations. Rigorous analysis techniques exist to aid in quantifying the uncertainties on the experimental data sets, as discussed in § 3.
Step 7: Set-up an input file for gyrokinetic simulations of the new experimental discharge. Run linear gyrokinetic simulations on the ‘base case’ and perform sensitivity scans to understand what mode or modes are unstable in the radial regions of interest. If nonlinear simulations have not yet been run in step 5, then first perform resolution scans, box-size scans, etc. so that you can develop an understanding of how to get a numerically robust result.
Step 8: Run nonlinear simulations on the ‘base case’ and compare with power balance results. A good approach is to perform sensitivity scans of input parameters within error bars to obtain a ‘flux-matched case’, when using gradient-driven simulations. It is an important result if the simulation can (or cannot) match the experiment ion and electron heat fluxes from power balance within error bars. If we want to apply a synthetic diagnostic to output data from the nonlinear simulation, the simulations need to adequately resolve the turbulence wavenumber detected by the DR system in this example. This may require a higher resolution simulation than is required to study heat fluxes. In addition, application of a synthetic diagnostic (Step 9) may require the generation of synthetic time history, with sufficient temporal resolution to allow for application of the same data analysis routines used on experimental time histories.
Step 9: Once a ‘flux-matched case’ is obtained, apply the synthetic diagnostic for the DR and compare with the measured turbulence characteristics. Perform sensitivity scans of synthetic diagnostic parameters (e.g. the wavenumber resolution can be scanned and/or the spot size, or sample volume size, can be scanned within experimental uncertainty). If possible, go back and scan the inputs to the gyrokinetic code and apply the synthetic diagnostic for the DR, to gauge how sensitive the turbulence is to changes in the input parameters. The sensitivity may be different than that of the fluxes.
Step 10: Apply a validation metric using as many of the measurements as possible to better quantify and interpret the meaning of agreement and/or disagreement between the experiment and the code. Practical examples can be found in the following references: Ricci et al. (Reference Ricci, Theiler, Fasoli, Furno, Gustafson, Iraji and Loizu2011), Holland (Reference Holland2016), Freethy et al. (Reference Freethy, Görler, Creely, Conway, Happel and White2018).
Step 11 and so on: Repeat steps above, as needed, to explore robustness of agreement and disagreement found between experiment and simulation.
3 Data analysis in support of gyrokinetic code validation
Designing dedicated experiments with the goal of gathering a data set suitable for extensive gyrokinetic code validation is important because a single, rich data set can be a good foundation for a variety validation studies, and can be compared with many different models and codes. This section will describe the basic building blocks of data analysis used for validation experiments in fusion plasmas: magnetic equilibrium reconstruction, § 3.1, radial profile measurements, § 3.2 and power balance calculations, § 3.3, as well as discussing preparation of input files for gyrokinetic codes, § 3.4.
3.1 Magnetic equilibrium reconstruction
For magnetic equilibrium reconstruction (Mukhovatov & Shafranov Reference Mukhovatov and Shafranov1971), a variety of experimental data can be used. Most routinely, an equilibrium reconstruction is obtained using data only from magnetic diagnostics (magnetic probes, flux loops, coil currents, diamagnetic flux, etc.) to constrain the solution of the Grad–Shafranov equation. A variety of codes in the experimental community are used routinely for this purpose, two examples being CLISTE (McCarthy, Martin & Schneider Reference McCarthy, Martin and Schneider1999) and EFIT (Lao et al.
Reference Lao, Ferron, Groebner, Howl, St. John, Strait and Taylor1990). To test that the magnetic reconstruction does not contain any systematic uncertainties, a variety of consistency checks are possible. One very simple method involves comparing high-field side (HFS) electron cyclotron emission (ECE) measurements to low-field side (LFS) ECE measurements. Since electron temperature,
![]() $T_{e}$
, is expected to be a constant on a flux surface, if the ECE measurements mapped onto the reconstruction from HFS and LFS disagree, then one should suspect that the position of the magnetic axis (according to the reconstruction) may be incorrect.
$T_{e}$
, is expected to be a constant on a flux surface, if the ECE measurements mapped onto the reconstruction from HFS and LFS disagree, then one should suspect that the position of the magnetic axis (according to the reconstruction) may be incorrect.

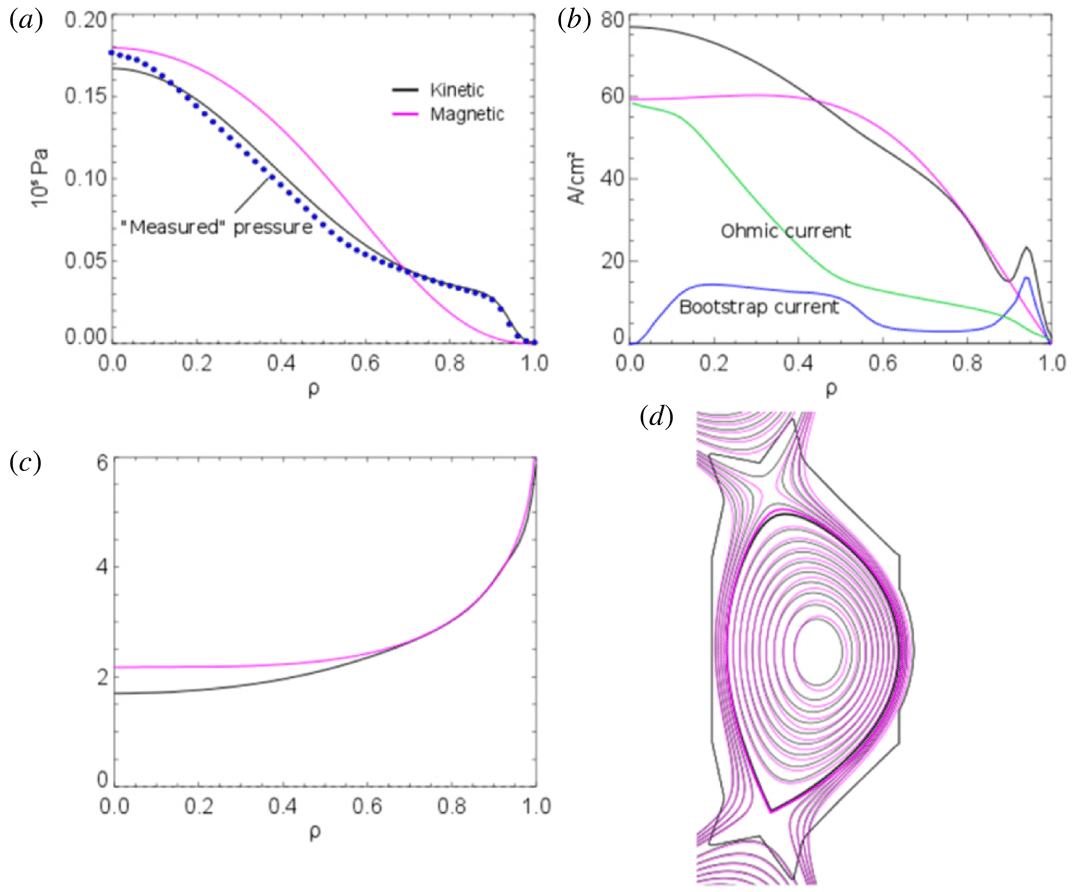
Figure 3. Kinetic equilibrium reconstruction (black) compared to a magnetics only reconstruction (pink). Reproduction of figure 2 of Li et al. (Reference Li, Ren, Qian, Lao, Ding, Chen, Liu, Lu and Zang2013).
The extension of this is the ‘kinetic equilibrium reconstruction’, where pressure profile measurements in addition to magnetic measurements are used to constrain the reconstruction. An example of the difference between a ‘magnetics only equilibrium reconstruction’ and a ‘kinetic equilibrium reconstruction’ is shown in figure 3. There can be significant differences in the safety factor profile and flux surface location in real space in tokamak plasmas featuring strong auxiliary heating and current drive.
In addition to kinetically constrained equilibrium reconstructions, a typical goal of dedicated validation experiments is to obtain measurements of the plasma current profile, from the motional Stark effect (MSE) (Holcomb et al. Reference Holcomb, Makowski, Allen, Meyer and van Zeeland2008) or polarimeter (Bergerson et al. Reference Bergerson, Xu, Irby, Brower, Ding and Marmar2012) measurements. Using more data to constrain the magnetic equilibrium reconstruction is useful for addressing both systematic and random uncertainties. Reducing the uncertainty on the equilibrium reconstruction will help reduce the errors in diagnostic mapping, that is, determining where a measurement made in real space maps to in flux geometry.

Figure 4. Error bars on the safety factor
![]() $q$
arising from random error in magnetics data at the EAST tokamak are visualized by overplotting the
$q$
arising from random error in magnetics data at the EAST tokamak are visualized by overplotting the
![]() $q$
and density profiles reconstructed with 3 %, 5 % and 10 % random perturbations from the original equilibrium. Reproduced from figure 5 of Qian et al. (Reference Qian, Lao, Oqilong, Baonian, Haiqin, Long, Zhengping, Hanada, Dalong and Tonghui2015).
$q$
and density profiles reconstructed with 3 %, 5 % and 10 % random perturbations from the original equilibrium. Reproduced from figure 5 of Qian et al. (Reference Qian, Lao, Oqilong, Baonian, Haiqin, Long, Zhengping, Hanada, Dalong and Tonghui2015).
Using more data to constrain a magnetic reconstruction means that any errors or uncertainties on that data will propagate though to the final result. It is desirable that errors on safety factor and magnetic shear be as low as possible. Random error on these reconstructed values (and on any output value from the reconstruction) can be estimated using a simple Monte Carlo approach, by varying the inputs all randomly within the error bars, and running the reconstruction code many times to obtain mean output values and variances on the mean. One example of results from this approach is shown in figure 4. Other, faster methods, such as semi-analytic approaches to estimate the uncertainty in the equilibrium free parameters can be employed (Anderson et al. Reference Anderson, Forest, Biewer, Sarff and Wright2004), and open-source toolsets for quantifying the error and uncertainty on the magnetic equilibrium reconstruction are available (Chilenski, Faust & Walk Reference Chilenski, Faust and Walk2017).
3.2 Radial profile measurements
Reliable techniques to measure electron density and electron temperature are widely available, exploiting Thomson scattering (measurements of
![]() $ne(r,t)$
,
$ne(r,t)$
,
![]() $Te(r,t)$
) and ECE diagnostics
$Te(r,t)$
) and ECE diagnostics
![]() $(Te(r,t))$
, and profile reflectometers
$(Te(r,t))$
, and profile reflectometers
![]() $(ne(r,t))$
(Donne Reference Donne, Costley, Barnsley, Bindslev, Boivin, Conway, Fisher, Giannella, Hartfuss and Von Hellermann2007). Thomson scattering density profile measurements can be additionally constrained using data from multi-chord interferometers or other measurements, or data from profile reflectometers. Ion temperature and rotation measurements are far more challenging, typically requiring beam based charge exchange (Fonck et al.
Reference Fonck, Darrow and Jaehnig1984), e.g. with carbon (Grierson et al.
Reference Grierson, Burrell, Chrystal, Groebner, Kaplan, Heidbring, Munoz Burgos, Pablant, Solomon and Van Zeeland2012) or boron and nitrogen (Viezzer et al.
Reference Viezzer, Putterich, Dux and McDermott2012), or X-ray imaging crystal spectroscopy using argon (Reinke et al.
Reference Reinke, Podpaly, Bitter, Hutchinson, Rice, Delgado-Aparicio, Gao, Greenwald, Hill and Howard2012). Note that in these cases the measured ion temperature and rotation are those of the measured impurity, which in many cases may be argued to have the same values as for the main ions (Hutchinson Reference Hutchinson1987). Specialized measurements and dedicated experiments are required to extract the main ion temperature and rotation profile data directly (Grierson et al.
Reference Grierson, Burrell, Chrystal, Groebner, Kaplan, Heidbring, Munoz Burgos, Pablant, Solomon and Van Zeeland2012). Care must also be taken to constrain estimates of the impurity content, or
$(ne(r,t))$
(Donne Reference Donne, Costley, Barnsley, Bindslev, Boivin, Conway, Fisher, Giannella, Hartfuss and Von Hellermann2007). Thomson scattering density profile measurements can be additionally constrained using data from multi-chord interferometers or other measurements, or data from profile reflectometers. Ion temperature and rotation measurements are far more challenging, typically requiring beam based charge exchange (Fonck et al.
Reference Fonck, Darrow and Jaehnig1984), e.g. with carbon (Grierson et al.
Reference Grierson, Burrell, Chrystal, Groebner, Kaplan, Heidbring, Munoz Burgos, Pablant, Solomon and Van Zeeland2012) or boron and nitrogen (Viezzer et al.
Reference Viezzer, Putterich, Dux and McDermott2012), or X-ray imaging crystal spectroscopy using argon (Reinke et al.
Reference Reinke, Podpaly, Bitter, Hutchinson, Rice, Delgado-Aparicio, Gao, Greenwald, Hill and Howard2012). Note that in these cases the measured ion temperature and rotation are those of the measured impurity, which in many cases may be argued to have the same values as for the main ions (Hutchinson Reference Hutchinson1987). Specialized measurements and dedicated experiments are required to extract the main ion temperature and rotation profile data directly (Grierson et al.
Reference Grierson, Burrell, Chrystal, Groebner, Kaplan, Heidbring, Munoz Burgos, Pablant, Solomon and Van Zeeland2012). Care must also be taken to constrain estimates of the impurity content, or
![]() $Z_{eff}$
profile, in the plasma. This discussion of profiles is limited to one-dimensional (1-D) radial profiles, and any poloidal asymmetries of the temperature or density are ignored, which is an acceptable approximation in the core of the plasma, where the standard gyrokinetic theory is valid. It is important to note this approximation fails in many cases for the impurity density or plasma rotation.
$Z_{eff}$
profile, in the plasma. This discussion of profiles is limited to one-dimensional (1-D) radial profiles, and any poloidal asymmetries of the temperature or density are ignored, which is an acceptable approximation in the core of the plasma, where the standard gyrokinetic theory is valid. It is important to note this approximation fails in many cases for the impurity density or plasma rotation.

Figure 5. Gaussian process regression (GPR) methods are used to fit electron temperature data in C-Mod, and rigorously quantify the error bars that will constrain the later sensitivity scans in a validation study. From figure 6 of Chilenski et al. (Reference Chilenski, Greenwald, Marzouk, Howard, White, Rice and Walk2015).
The experimental value of local temperature (or density, rotation, etc.) and the local radial gradients are derived from smooth fits to the 1-D radial profiles of the data. In figure 5, data from an Alcator C-Mod ICRF heated L-mode plasma from a dedicated experiment are shown, along with fits to the data using several different techniques. The use of integrated data analysis (IDA) procedures and the Bayesian approach is extremely beneficial to constrain the reported ‘fits’ to experimental measurements (Fischer & Dinklage Reference Fischer and Dinklage2007; Rathgeber et al.
Reference Rathgeber, Fischer, Fietz, Hobirk, Kallenbach, Meister, Putterich, Ryter, Tardini and Wolfrum2010; Reusch et al.
Reference Reusch, Galante, Franz, Johnson and McGarry2014). Gaussian process regression (GPR) can be used to fit the profiles and calculate the error bars (Chilenski et al.
Reference Chilenski, Greenwald, Marzouk, Howard, White, Rice and Walk2015). Simpler methods, such as spline fits combined with a Monte Carlo approach have also been used in the past (White et al.
Reference White, Schmitz, Peebles, Rhodes, Carter, McKee, Shafer, Staebler, Burrell and DeBoo2010b
; Holland Reference Holland2016). With any profile fitting method, it is not uncommon to end up with uncertainties on normalized gradient scale lengths, e.g.
![]() $a/L_{\text{ne}}$
,
$a/L_{\text{ne}}$
,
![]() $a/L_{\text{Te}}$
and
$a/L_{\text{Te}}$
and
![]() $a/L_{\text{Ti}}$
, between 10 and 30 %.
$a/L_{\text{Ti}}$
, between 10 and 30 %.
All profile measurements are not required on every shot in a dedicated experiment; in many experiments it is sufficient to run a reference shot (to obtain the desired profile and/or turbulence measurements), and then run repeat shots to obtain all the other data of interest. Of course, the reference and repeat discharges must have matched parameters within experimental error bars. The data from the reference shot (or averaged data from several reference shots or several time slices within a reference shot) are used for gyrokinetic simulation.
3.3 Power balance calculations
Minimizing the errors and uncertainty of the simulation inputs taken from the magnetic equilibrium and the measured radial pressure profiles is just one step in experimental design and execution. Because experimental fluxes can only be directly measured in very specialized experiments using diagnostics that are not widely available (Forster et al. Reference Forster, Schoch, Hickok and Jennings1994; Evensen et al. Reference Evensen, Fonck, Paul, Rewoldt, Scott, Tang and Zarnstorff1998; Howard et al. Reference Howard, Greenwald, Mikkelsen, Reinke, White, Ernst, Podpaly and Candy2012), power balance calculations are used to infer the experimental values of the heat and particle fluxes. It is very important to minimize the error on the experimental values fluxes calculated by power balance for gyrokinetic validation studies.
A power balance calculation solves the electron and ion energy conservation equations, the poloidal magnetic diffusion equation and the particle and momentum balance equations. Additional models are employed to handle neutral transport, plasma conductivity and auxiliary heating and current drive. Reducing error bars on interpretive power balance calculations is complicated by the need to use many measurements as input to the power balance calculation. For example, to solve for the electron and ion heat fluxes, power balance calculations will take as input the profiles we have already discussed,
![]() $Te(r,t)$
,
$Te(r,t)$
,
![]() $Ti(r,t)$
,
$Ti(r,t)$
,
![]() $ne(r,t)$
and also will need radiated power profile measurements, current profile and information about
$ne(r,t)$
and also will need radiated power profile measurements, current profile and information about
![]() $Z_{\text{eff}}$
. The power balance codes also use the total heating power and other characteristics of specific actuators (e.g. ion cyclotron range of frequency (ICRF) heating or electron cyclotron resonance heating (ECRH) as input). The profile of energy deposition is then calculated self-consistently using models such as TORIC (Brambilla Reference Brambilla1999).
$Z_{\text{eff}}$
. The power balance codes also use the total heating power and other characteristics of specific actuators (e.g. ion cyclotron range of frequency (ICRF) heating or electron cyclotron resonance heating (ECRH) as input). The profile of energy deposition is then calculated self-consistently using models such as TORIC (Brambilla Reference Brambilla1999).
The primary equation solved in power balance is the electron energy conservation equation (Ongena et al. Reference Ongena, Voitsekhovitch, Evrard and McCune2012):
The electron heat flux is
![]() $\boldsymbol{q}_{\text{e}}=n_{\text{e}}\unicode[STIX]{x1D735}T_{\text{e}}\unicode[STIX]{x1D712}_{\text{e}}$
, and the thermal diffusivity,
$\boldsymbol{q}_{\text{e}}=n_{\text{e}}\unicode[STIX]{x1D735}T_{\text{e}}\unicode[STIX]{x1D712}_{\text{e}}$
, and the thermal diffusivity,
![]() $\unicode[STIX]{x1D712}_{\text{e}}$
, is equal to the electron thermal conductivity divided by electron density. As described in Ongena et al. (Reference Ongena, Voitsekhovitch, Evrard and McCune2012) the first term in the electron energy conservation equation above is the rate of change of the electron energy, the second term gives the heat flux, the third is the electron convection losses (arising from the particle flux) and the fourth is work done by the plasma particles against the pressure gradient. Terms on the right-hand side,
$\unicode[STIX]{x1D712}_{\text{e}}$
, is equal to the electron thermal conductivity divided by electron density. As described in Ongena et al. (Reference Ongena, Voitsekhovitch, Evrard and McCune2012) the first term in the electron energy conservation equation above is the rate of change of the electron energy, the second term gives the heat flux, the third is the electron convection losses (arising from the particle flux) and the fourth is work done by the plasma particles against the pressure gradient. Terms on the right-hand side,
![]() $S$
, are the power gain and loss terms for the electrons, such as ohmic heating power, auxiliary power to electrons (ECRH, ICRF, etc.), radiation losses, ionization losses and exchange losses to ions. The electron energy conservation equation is solved for the unknown thermal diffusivity (for the unknown heat flux in term two on the left-hand side) using experimental measurements and models to assess the other terms. A similar energy conservation equation is solved for the ions to obtain the unknown ion heat flux.
$S$
, are the power gain and loss terms for the electrons, such as ohmic heating power, auxiliary power to electrons (ECRH, ICRF, etc.), radiation losses, ionization losses and exchange losses to ions. The electron energy conservation equation is solved for the unknown thermal diffusivity (for the unknown heat flux in term two on the left-hand side) using experimental measurements and models to assess the other terms. A similar energy conservation equation is solved for the ions to obtain the unknown ion heat flux.
In practice, codes like TRANSP (Hawryluk Reference Hawryluk1979) and ASTRA (Pereverzev et al. Reference Pereverzev, Yushmanoy, Dnestrovskii, Polevoi, Tarasian and Zakharov1991) are commonly run after an experiment in ‘interpretive mode’, using experimental kinetic profiles as input, along with appropriate models for the power gain and loss terms. This is in contrast to running power balance in predictive mode, for which kinetic profiles are predicted using transport models (Budny et al. Reference Budny, Andre, Bateman, Halpern, Kessel, Kritz and McCune2008). Once an interpretive power balance run is complete, several internal consistency checks are possible to reveal systematic errors in power balance calculations. The measured neutron rate and loop voltages can be compared to modelled values. The stored energy can be calculated and compared to that of the magnetic reconstruction (which is also a step that is part of assessing the fast ion pressure contribution to the total ion pressure). Systematic uncertainties can be identified via these and other methods (Petty et al. Reference Petty, Luce, DeBoo, Waltz, Baker and Wade1998; Grierson et al. Reference Grierson, Yuan, Gorelenkova, Kaye, Logan, Meneghini, Haskey, Buchanan, Fitzgerald and Smith2018). For an excellent pedagogical review of power balance calculations see Ongena et al. (Reference Ongena, Voitsekhovitch, Evrard and McCune2012) and for more rigorous derivation of transport equations see Hinton & Hazeltine (Reference Hinton and Hazeltine1976). As an additional point of interest, perturbative transport experiments are also used to calculate an experimental ‘heat pulse’ or ‘perturbative diffusivity’. This is not to be confused with the ‘steady state’ or equilibrium diffusivity solved for by power balance. Recent examples of using the perturbative diffusivity to compare with turbulent transport models can be found in Smith et al. (Reference Smith, Petty, White, Holland, Bravenec, Austin, Zeng and Meneghini2015), Creely et al. (Reference Creely, Howard, Rodriguez-Fernandez, Cao, Hubbard, Hughes, Rice, White, Candy and Staebler2017) and references therein.

Figure 6. The errors on temperature profiles are propagated through the power balance calculation to obtain errors on the inferred ion and electron heat fluxes. From figure 6 of Holland (Reference Holland2016).
Error analysis of interpretive power balance runs is non-trivial, and several different approaches have been discussed in the literature, along with identification of common systematic errors (Holland Reference Holland2016). Analytic error propagation gives good agreement with Monte Carlo approaches (White et al.
Reference White, Schmitz, Peebles, Rhodes, Carter, McKee, Shafer, Staebler, Burrell and DeBoo2010b
). More sophisticated methods for calculating the errors on power balance results have been recently proposed (Vaezi & Holland Reference Vaezi and Holland2018). Despite best efforts, the experimental error can be reduced only so much, and the ion and electron heat fluxes,
![]() $Q_{\text{i}}$
and
$Q_{\text{i}}$
and
![]() $Q_{\text{e}}$
, will typically have errors of
$Q_{\text{e}}$
, will typically have errors of
![]() $\unicode[STIX]{x1D70E}_{Q}\sim 10{-}30\,\%$
. Shown in figure 6 is an example of ion and electron heat fluxes that were experimentally inferred at DIII-D using power balance in a targeted validation experiment (Holland Reference Holland2016), which illustrates the radial variation of the fluxes and uncertainties.
$\unicode[STIX]{x1D70E}_{Q}\sim 10{-}30\,\%$
. Shown in figure 6 is an example of ion and electron heat fluxes that were experimentally inferred at DIII-D using power balance in a targeted validation experiment (Holland Reference Holland2016), which illustrates the radial variation of the fluxes and uncertainties.
Once the power balance analysis is complete and verified to be free of systematic errors (Holland Reference Holland2016), it is important to take care when selecting which outputs correspond to the ‘experimental values’ to be used for comparison with the gyrokinetic codes. For example, a gyrokinetic transport model will calculate the heat flux due to the turbulence. Typically, power balance codes give the convection losses arising from the particle flux as a separate contribution to the total heat flux (Ongena et al. Reference Ongena, Voitsekhovitch, Evrard and McCune2012). The convection losses are small compared to conducted losses, but may not be negligible. For example then, when we run transport models to calculate turbulent and neoclassical fluxes, we get a total flux, which should be compared to the sum of the ‘heat flux loss’ and ‘convection loss’ terms in the electron energy conservation equation solved by TRANSP (Ongena et al. Reference Ongena, Voitsekhovitch, Evrard and McCune2012); though again, the convection loss term is usually very small.
A significant systematic error can arise from handling the fast ion contribution to the ion pressure. If the fast ion pressure is substantial, then this must be modelled within power balance correctly (e.g. using additional modules that calculate the fast ion transport due to collisions). For discussion of the fast ion transport power balance calculation process and associated uncertainties, see Pace et al. (Reference Pace, Austin, Bass, Budny, Heidbrink, Hillesheim, Holcomb, Gorelenkova, Grierson and McCune2013). Integrated modelling approaches are also very useful in plasmas with substantial fast ion pressures, as described in Garcia et al. (Reference Garcia, Challis, Citrin, Doerk, Giruzzi, Görler, Jenko and Maget2015), where differences between the fast ion pressure and the thermal ion pressure can be significant. In addition to ensuring correct interpretation of power balance results, assessment of the fast ion pressure is important in plasmas where the superthermal pressure gradients has direct impact on the turbulence being simulated by gyrokinetic codes (Citrin et al. Reference Citrin, Jeko, Mantica, Told, Bourdelle, Dumont, Garcia, Haverkort, Hogeweij and Johnson2014).
3.4 Preparing input files for gyrokinetic codes
To prepare an input file a flux-driven gyrokinetic simulation of an experimental discharge requires at minimum the experimental equilibrium reconstruction and local pressure profile measurements. Using the experimental data, suitably processed, input files for the gyrokinetic code are prepared for each code using specialized tools. Sometimes the specialized tools use outputs from a power balance code, in which case a power balance analysis will also be required before the input files for the simulation can be prepared. Obviously the details of how to prepare an input file for a gyrokinetic code will depend on the specific experiment as well as the code of interest, but there are several general issues that are useful to keep in mind. One pitfall has to do with definitions of fundamental parameters of interest. For example, the measured values of temperature and local magnetic field (based on an equilibrium reconstruction) may be used by an experimentalist to calculate the value of the ion sound gyroradius
![]() $\unicode[STIX]{x1D70C}_{\text{s}}=(m_{\text{i}}T_{\text{e},\text{local}}/2B_{\text{local}})^{1/2}$
at a particular radiation location in an experiment. However, within the native units of a gyrokinetic code, the value of
$\unicode[STIX]{x1D70C}_{\text{s}}=(m_{\text{i}}T_{\text{e},\text{local}}/2B_{\text{local}})^{1/2}$
at a particular radiation location in an experiment. However, within the native units of a gyrokinetic code, the value of
![]() $\unicode[STIX]{x1D70C}_{\text{s}}$
may be very different at the same radial position. This should be carefully tracked when comparing the reference magnetic fields used in local, flux-tube simulations with values obtained from experiments. Miller geometry is often used to parameterize the magnetic equilibrium (Miller et al.
Reference Miller, Chu, Greene, Lin-Liu and Waltz1998), which can also affect the mapping from experimental coordinates to simulation coordinates. Finally, we note that care must be taken to ensure that the local gradient of the profiles is consistently calculated between the experiment and the codes. It is good practice (part of identification and quantification of uncertainty (Terry et al.
Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008)) for authors to specify the simulation numerical details, as well as the input parameters and definitions, in validation papers.
$\unicode[STIX]{x1D70C}_{\text{s}}$
may be very different at the same radial position. This should be carefully tracked when comparing the reference magnetic fields used in local, flux-tube simulations with values obtained from experiments. Miller geometry is often used to parameterize the magnetic equilibrium (Miller et al.
Reference Miller, Chu, Greene, Lin-Liu and Waltz1998), which can also affect the mapping from experimental coordinates to simulation coordinates. Finally, we note that care must be taken to ensure that the local gradient of the profiles is consistently calculated between the experiment and the codes. It is good practice (part of identification and quantification of uncertainty (Terry et al.
Reference Terry, Greenwald, Leboeuf, McKee, Mikkelsen, Nevins, Newman and Stotler2008)) for authors to specify the simulation numerical details, as well as the input parameters and definitions, in validation papers.
4 Turbulence measurements in the core of fusion plasmas
At most major fusion devices around the world there are several fluctuation diagnostics that can be used in validation studies. Density fluctuation measurements are the most widely available. Beam emission spectroscopy (BES) diagnostics (McKee et al.
Reference McKee, Fonck, Gupta, Schlossberg, Shafer, Boivin and Solomon2007; Field et al.
Reference Field, Dunai, Ghim, Hill, McMillan, Roach, Saarelma, Schekochihin and Zoletnik2014), and standard reflectometry (Nazikian, Kramer & Valeo Reference Nazikian, Kramer and Valeo2001) are used to probe long-wavelength or low-
![]() $k$
turbulence (typically
$k$
turbulence (typically
![]() $k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<0.5$
), relevant for ITG/TEM type turbulence or MTM type turbulence. In the intermediate wavelength range, Doppler reflectometer (also known as Doppler backscattering) (Holzhauer et al.
Reference Holzhauer, Hirsch, Grossman, Branaz and Serra1998; Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001; Conway et al.
Reference Conway, Schirmer, Klenge, Suttrop and Holzhauer2004; Hennequin et al.
Reference Hennequin, Honore, Truc, Quemeneur and Lemoine2004; Happel et al.
Reference Happel, Estrade, Blanco, Tribaldos, Cappa and Bustos2009; Hillesheim et al.
Reference Hillesheim, Peebles, Rhodes, Schmitz, Carter, Gourdain and Wang2009; Rhodes et al.
Reference Rhodes, Peebles, Nguyen, Hillesheim, Schmitz, White and Wang2010; Tokuszawa et al.
Reference Tokuszawa, Ejiri, Kawahata, Tanaka, Yamada, Yoshinuma, Ida and Suzuki2012; Zhou et al.
Reference Zhou, Liu, Zhang, Hu, Wang, Li, Lan, Xie, Sun and Ding2013) can access wavenumbers between the high ion scale
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<0.5$
), relevant for ITG/TEM type turbulence or MTM type turbulence. In the intermediate wavelength range, Doppler reflectometer (also known as Doppler backscattering) (Holzhauer et al.
Reference Holzhauer, Hirsch, Grossman, Branaz and Serra1998; Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001; Conway et al.
Reference Conway, Schirmer, Klenge, Suttrop and Holzhauer2004; Hennequin et al.
Reference Hennequin, Honore, Truc, Quemeneur and Lemoine2004; Happel et al.
Reference Happel, Estrade, Blanco, Tribaldos, Cappa and Bustos2009; Hillesheim et al.
Reference Hillesheim, Peebles, Rhodes, Schmitz, Carter, Gourdain and Wang2009; Rhodes et al.
Reference Rhodes, Peebles, Nguyen, Hillesheim, Schmitz, White and Wang2010; Tokuszawa et al.
Reference Tokuszawa, Ejiri, Kawahata, Tanaka, Yamada, Yoshinuma, Ida and Suzuki2012; Zhou et al.
Reference Zhou, Liu, Zhang, Hu, Wang, Li, Lan, Xie, Sun and Ding2013) can access wavenumbers between the high ion scale
![]() $k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}\sim 0.5$
and the low-
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}\sim 0.5$
and the low-
![]() $k$
electron scale,
$k$
electron scale,
![]() $k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}\sim 5$
. At the highest wavenumbers, relevant to ETG-scale turbulence, density fluctuations can be measured with high
$k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}\sim 5$
. At the highest wavenumbers, relevant to ETG-scale turbulence, density fluctuations can be measured with high
![]() $k$
coherent scattering diagnostics (Rhodes et al.
Reference Rhodes, Peebles, Van Zeeland, Degrassie, Bravenec, Burrell, DeBoo, Lohr, Petty and Nguyen2007; Smith et al.
Reference Smith, Mazzucator, Lee, Park, Domier and Luhmann2008; Qing et al.
Reference Qing, Junyu, Li, Qingsheng, Yanqing, Tao, Xiaoqi, Bhatti and Xiang2010).
$k$
coherent scattering diagnostics (Rhodes et al.
Reference Rhodes, Peebles, Van Zeeland, Degrassie, Bravenec, Burrell, DeBoo, Lohr, Petty and Nguyen2007; Smith et al.
Reference Smith, Mazzucator, Lee, Park, Domier and Luhmann2008; Qing et al.
Reference Qing, Junyu, Li, Qingsheng, Yanqing, Tao, Xiaoqi, Bhatti and Xiang2010).
Electron temperature fluctuations can currently only be accessed at long-wavelength or low
![]() $k$
, with correlation electron cyclotron emission (CECE) diagnostics (Sattler & Hartfuss Reference Sattler and Hartfuss1993, Reference Sattler and Hartfuss1994; Cima et al.
Reference Cima, Bravenec, Wootton, Rempel, Gandy, Watts and Kwon1995; White et al.
Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Zemedkun et al.
Reference Zemedkun, Che, Chen, Domier, Luhmann, Munsat, Parker, Tobias, Wan and Yu2015; Freethy et al.
Reference Freethy, Conway, Classen, Creely, Happel, Koehn, Vanovac and White2016; Sung et al.
Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016; Fontana, Porte & Cabrera Reference Fontana, Porte and Cabrera2017) on tokamaks and stellarators; unfortunately this measurement is unavailable in spherical tokamaks, because the 2nd harmonic X-mode electron cyclotron emission is cutoff in these low toroidal field, high plasma beta plasmas. At low-
$k$
, with correlation electron cyclotron emission (CECE) diagnostics (Sattler & Hartfuss Reference Sattler and Hartfuss1993, Reference Sattler and Hartfuss1994; Cima et al.
Reference Cima, Bravenec, Wootton, Rempel, Gandy, Watts and Kwon1995; White et al.
Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Zemedkun et al.
Reference Zemedkun, Che, Chen, Domier, Luhmann, Munsat, Parker, Tobias, Wan and Yu2015; Freethy et al.
Reference Freethy, Conway, Classen, Creely, Happel, Koehn, Vanovac and White2016; Sung et al.
Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016; Fontana, Porte & Cabrera Reference Fontana, Porte and Cabrera2017) on tokamaks and stellarators; unfortunately this measurement is unavailable in spherical tokamaks, because the 2nd harmonic X-mode electron cyclotron emission is cutoff in these low toroidal field, high plasma beta plasmas. At low-
![]() $k$
, it is also possible to measure the phase angle between electron temperature and density fluctuations, by coupling an ECE radiometer with a reflectometer (White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
).
$k$
, it is also possible to measure the phase angle between electron temperature and density fluctuations, by coupling an ECE radiometer with a reflectometer (White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
).
Turbulence fluxes cannot be measured directly with any of these systems. Systems like the heavy-ion beam probe (Forster et al. Reference Forster, Schoch, Hickok and Jennings1994) can measure the electrostatic potential fluctuations and density fluctuations simultaneously, and hence the turbulent particle flux, but these measurements have not been fielded widely.
The review article of Tynan et al. (Reference Tynan, Fujisawa and McKee2009) includes an extensive discussion of turbulence measurements in fusion devices and basic plasma devices. In this tutorial, we discuss in detail only a handful of fluctuation measurements: beam-emission spectroscopy diagnostics (BES), correlation electron cyclotron emission (CECE) radiometers,
![]() $n-T$
phase diagnostics, Doppler reflectometers and coherent scattering measurements. These measurements are discussed in order to highlight general turbulence data analysis techniques used in validation studies.
$n-T$
phase diagnostics, Doppler reflectometers and coherent scattering measurements. These measurements are discussed in order to highlight general turbulence data analysis techniques used in validation studies.
Additional turbulence diagnostics used to measure core turbulence in fusion devices, some of which have been compared to gyrokinetic simulation, but not discussed in this tutorial, include: heavy ion beam probes (Forster et al. Reference Forster, Schoch, Hickok and Jennings1994), fast profile reflectometer (Casati et al. Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gurcan and Heuraux2009), phase contrast imaging (PCI) (Ennever Reference Ennever, Porkolab, Candy, Staebler, Reinke, Rice, Rost, Ernst, Hughes and Baek2016), fast two colour interferometry (FTCI) (Kasten, White & Irby Reference Kasten, White and Irby2014), polarimeter (Bergerson et al. Reference Bergerson, Xu, Irby, Brower, Ding and Marmar2012) cross-polarization scattering (Rhodes et al. Reference Rhodes, Peebles, Crocker and Nguyen2014), ultra-fast charge exchange recombination spectroscopy (UF CHERS) (Evensen et al. Reference Evensen, Fonck, Paul, Rewoldt, Scott, Tang and Zarnstorff1998; Uzun-Kaymak, Fonck & McKee Reference Uzun-Kaymak, Fonck and McKee2012).
4.1 Beam-emission spectroscopy diagnostic
Beam-emission spectroscopy (BES) systems are used to measure local density fluctuations from collisionally excited, Doppler-shifted emission from neutral beams, usually hydrogen or deuterium (McKee et al.
Reference McKee, Fonck, Gupta, Schlossberg, Shafer, Boivin and Solomon2007; Tynan et al.
Reference Tynan, Fujisawa and McKee2009). The fast neutral atoms injected by the beams are excited via plasma collisions. The excited neutrals emit H-alpha or D-alpha photons due to collisional and radiative processes. These photons are blue shifted due to the beam velocity, which allows a separation from other H-alpha or D-alpha emission. The normalized fluctuation intensity of the emission is related to the normalized density fluctuation using a collisional radiative model (Hutchinson Reference Hutchinson2002). BES is a useful measurement for validation because it is highly localized in radius, and has good time resolution intrinsically, though when measuring small fluctuation levels, time averaging over steady phases of the discharge is required. Unlike reflectometry, measurement of an absolute fluctuation level
![]() ${\tilde{n}}/n$
rather than in arbitrary units (a.u.) is possible with atomic physics modelling. However, neutral beam injection is required, which may be perturbative or unavailable in the plasmas of interest.
${\tilde{n}}/n$
rather than in arbitrary units (a.u.) is possible with atomic physics modelling. However, neutral beam injection is required, which may be perturbative or unavailable in the plasmas of interest.

Figure 7. BES measurements of turbulent density fluctuations in two L-mode plasmas in DIII-D are shown. In both cases, the measured turbulent frequency spectrum is mapped to the wavenumber spectrum by exploiting the fact that the Doppler shift dominates over the frequency of the fluctuations in the plasma frame in these cases. From figure 3(a) of McKee et al. (Reference McKee, Burrell, Fonck, Jackson, Murakami, Staebler, Thomas and West2000).
With BES or any other fluctuation diagnostic, the frequency spectrum is measured in the laboratory frame, as shown in figure 7. The spectral shape is determined by the sum of the fluctuation frequency in the plasma frame and the Doppler shift arising from the radial electric field. When the Doppler shift is dominant, the measured frequency is roughly proportional to the poloidal wavenumber of the fluctuations. (McKee et al. Reference McKee, Burrell, Fonck, Jackson, Murakami, Staebler, Thomas and West2000).

Figure 8. Radial profile of fluctuation spectra measured with BES in DIII-D in an L-mode plasma. The spectra are integrated over the frequency range of interest to calculate the reported fluctuation level
![]() ${\tilde{n}}/n$
. From figure 3 of McKee et al. (Reference McKee, Fonck, Gupta, Schlossberg, Shafer, Boivin and Solomon2007).
${\tilde{n}}/n$
. From figure 3 of McKee et al. (Reference McKee, Fonck, Gupta, Schlossberg, Shafer, Boivin and Solomon2007).
By integrating the autospectrum over a given frequency range of interest, with appropriate normalization, the fluctuation level is calculated. Note that if the entire frequency range were to be used, the fluctuation level recovered should be identical to the root-mean-square (r.m.s.) fluctuation level calculated from the time history data (Pareseval’s theorem). Performing measurements at different radii allows the profile of the fluctuation levels to be reconstructed, as shown in figure 8. If it is not possible to obtain all the profile data points in one reference discharge, several repeat discharges are used, as long as the plasmas are identical within the experimental error bars (White et al. Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008).
The measured fluctuation spectrum will be perturbed by the presence of Magnetohydrodynamic (MHD) mode activity, and the total fluctuation level measured will reflect the effects of drift-wave turbulence combined with MHD (Field et al. Reference Field, Dunai, Ghim, Hill, McMillan, Roach, Saarelma, Schekochihin and Zoletnik2014). It is important in Gyrokinetic (GK) validation experiments to design discharges with little to no MHD activity (e.g. tearing modes and sawteeth) if the effects on turbulence and transport are not included in the transport models.
The correlation length of the turbulence is constructed using pairs of signals at different measurement locations. From the plot of the correlation coefficient at zero time delay versus spatial separation, it is possible to define the correlation length
![]() $L_{c}$
, as the width of a Gaussian function fitted to the envelope of the time-delay correlation function
$L_{c}$
, as the width of a Gaussian function fitted to the envelope of the time-delay correlation function
![]() $C(\unicode[STIX]{x1D70F}=0)$
plotted versus the distance
$C(\unicode[STIX]{x1D70F}=0)$
plotted versus the distance
![]() $x$
between channels:
$x$
between channels:
![]() $C(\unicode[STIX]{x1D70F}=0)=\exp (-(x/L_{c})^{2})$
(Shafer et al.
Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012). Other definitions may be used; it is best to verify with the diagnostician how the correlation length parameter is being calculated. It is also important to note that there can be limitations when using the two-point correlation technique method (Kim et al.
Reference Kim, Nam, Lampert and Ghim2016). With 2-D imaging BES systems, it is possible to measure radial and poloidal correlation lengths, and even to extract detailed information about the eddy sizes, shapes, and tilts, from measured 2-D correlation functions. These parameters have been compared with gyrokinetic simulations (Shafer et al.
Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012).
$C(\unicode[STIX]{x1D70F}=0)=\exp (-(x/L_{c})^{2})$
(Shafer et al.
Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012). Other definitions may be used; it is best to verify with the diagnostician how the correlation length parameter is being calculated. It is also important to note that there can be limitations when using the two-point correlation technique method (Kim et al.
Reference Kim, Nam, Lampert and Ghim2016). With 2-D imaging BES systems, it is possible to measure radial and poloidal correlation lengths, and even to extract detailed information about the eddy sizes, shapes, and tilts, from measured 2-D correlation functions. These parameters have been compared with gyrokinetic simulations (Shafer et al.
Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012).
4.2 Correlation electron cyclotron emission (CECE) measurements of ion-scale electron temperature fluctuation measurements
Correlation electron cyclotron emission (CECE) measurements exploit well understood diagnostic principles of detecting electron cyclotron emission from the optically thick second harmonic X-mode electron cyclotron resonance layer in fusion plasmas (Hutchinson Reference Hutchinson1987). Radiometers are commonly used to measure the radial profile of electron temperature from ECE in fusion plasmas with excellent spatial and temporal resolution. A radiometer measures the temperature of a radiating thermal source by applying a band-pass filter to the incoming white noise signal. This means that a single radiometer channel suffers from a baseline noise level, called the thermal noise level. The thermal noise level is set by the bandwidths of the pre-detection filter and post-detection filter (Cima et al. Reference Cima, Bravenec, Wootton, Rempel, Gandy, Watts and Kwon1995). A standard multi-channel radiometer is optimized for making radial profile measurements of the electron temperature. This means that the collection optics are not deigned allow for a tight focus in the plasma. It also means that the receiver electronics will have rather narrowband post-detection filters (setting the frequency response of the system to low values, in the 10 s of kHz range) and fairly wideband pre-detection filters (setting the radial resolution to be comparable to the ECE linewidth, approximately 1 cm or so in typical medium-scale fusion devices). Dedicated radiometers for fluctuation measurements are designed with focusing optics that achieve a sample volume comparable to the turbulent length scales of interest. The receiver will have pairs of channels with wideband post-detection filters (setting the frequency response of the system to high values in the MHz range) and with very narrow-band pre-detection filters (setting the radial resolution to sub-cm scale in typical medium-scale fusion devices). This latter choice is made so that two measurement locations can be co-located within the radial correlation length of the turbulence without having the bandwidths overlap in frequency, which ensures that the thermal noise is not correlated between the two channels.
The CECE measurement relies on correlating two such radiometer channels with the same turbulent signals, but with different thermal noise signals (Sattler & Hartfuss Reference Sattler and Hartfuss1993; Cima et al.
Reference Cima, Bravenec, Wootton, Rempel, Gandy, Watts and Kwon1995), and has been most widely deployed using a frequency-based decorrelation method (White et al.
Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Zemedkun et al.
Reference Zemedkun, Che, Chen, Domier, Luhmann, Munsat, Parker, Tobias, Wan and Yu2015; Freethy et al.
Reference Freethy, Conway, Classen, Creely, Happel, Koehn, Vanovac and White2016; Sung et al.
Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016). Correlation ECE radiometers have good spatial resolution, and can provide quantitative fluctuation levels in very straightforward manner, and are non-perturbative and passive measurements. Time averaging ranging from 50 ms to 1 s depending on the details of the turbulence is required to reduce thermal noise and extract the turbulent fluctuation data (White et al.
Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008). In addition, plasma density and magnetic field values limit accessibility, as with other mm-wave diagnostics like reflectometry and Doppler reflectometry. CECE radiometers tend to be most sensitive to low-
![]() $k$
, ion-scale, electron temperature fluctuations
$k$
, ion-scale, electron temperature fluctuations
![]() $(k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<0.5)$
.
$(k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<0.5)$
.
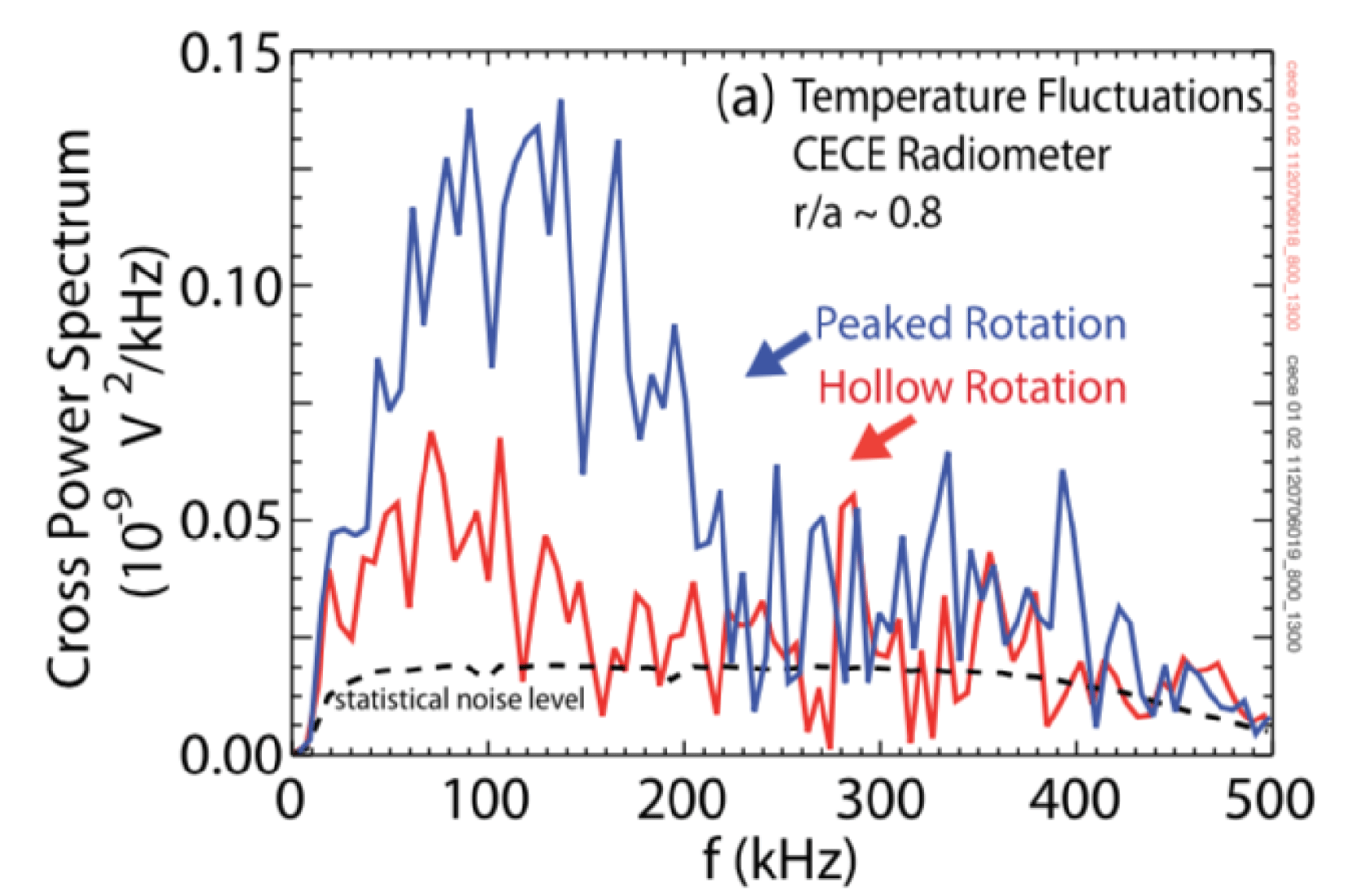
Figure 9. The spectrum of turbulent electron temperature fluctuations is measured in two L-mode plasmas with different intrinsic rotation profiles in Alcator C-Mod. The spectra are integrated over a frequency range of interest to calculate fluctuation levels. From figure 6(a) of White et al. (Reference White, Howard, Greenwald, Reinke, Sung, Baek, Barnes, Candy, Dominguez and Ernst2013).
Care must be taken with CECE measurements to fully exclude contributions of the thermal noise to the reported fluctuation level when calculating the cross-power spectrum between two radiometer channels. The resulting CECE cross-power spectrum can then be interpreted as the frequency spectrum of the electron temperature fluctuations. Figure 9 shows an example of CECE data from the C-Mod tokamak, where L-mode plasmas featuring different radial profiles of intrinsic rotation (White et al. Reference White, Howard, Greenwald, Reinke, Sung, Baek, Barnes, Candy, Dominguez and Ernst2013) are found to have different fluctuation levels. Integrating under the measured cross-power spectrum gives the fluctuation level, similar to analysis performed with BES data. Making this measurement at different radial locations with a multi-channel system, the CECE fluctuation amplitude radial profile can be measured. Figure 10 shows an example from TCV. The temperature fluctuation radial profiles are shown for two different triangularity plasmas (Fontana et al. Reference Fontana, Porte and Cabrera2017), which are found to have different fluctuation levels (again, corresponding to different transport characteristics). The radial and poloidal correlation lengths of the electron temperature fluctuations have also been measured in a number of experiments using standard 1-D ECE radiometers (Freethy et al. Reference Freethy, Görler, Creely, Conway, Happel and White2018) and 2-D imaging ECE radiometers (Deng et al. Reference Deng, Brower, Cima, Domier, Luhmann and Watts1998).

Figure 10. Radial profiles of the relative electron temperature fluctuation amplitude in plasmas with different triangularity values in TCV, as measured with a correlation ECE radiometer. From figure 5 of Fontana et al. (Reference Fontana, Porte and Cabrera2017).

Figure 11. Example of data from a reflectometer and CECE radiometer at DIII-D that share the same sight line to the plasma, allowing for measurements of the cross-phase angle between density and electron temperature fluctuations, the
![]() $n-T$
phase angle. From figure 3 of White et al. (Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
).
$n-T$
phase angle. From figure 3 of White et al. (Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
).
4.3 The
 $n-T$
-phase measurements
$n-T$
-phase measurements
Coupled reflectometer and radiometer (ECE) systems can be used to measure the cross-phase angle between low-
![]() $k$
$k$
![]() $n_{\text{e}}$
and
$n_{\text{e}}$
and
![]() $T_{\text{e}}$
fluctuations in stellarators and tokamaks (Haese et al.
Reference Haese, Hirsch and Hartfuss1999; White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
; Hillesheim et al.
Reference Hillesheim, DeBoo, Peebles, Carter, Wang, Rhodes, Schmitz, McKee, Yan and Staebler2013; Cao et al.
Reference Cao, Liu, Zhao, Zhou, Ti and Hu2016; Freethy et al.
Reference Freethy, Conway, Classen, Creely, Happel, Koehn, Vanovac and White2016). An example of the measurement in an ohmic L-mode plasma at DIII-D is shown in figure 11. The wavenumber resolution is determined by the spot-size for the ECE radiometer optics, and the wavenumber response of the reflectometer.
$T_{\text{e}}$
fluctuations in stellarators and tokamaks (Haese et al.
Reference Haese, Hirsch and Hartfuss1999; White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
; Hillesheim et al.
Reference Hillesheim, DeBoo, Peebles, Carter, Wang, Rhodes, Schmitz, McKee, Yan and Staebler2013; Cao et al.
Reference Cao, Liu, Zhao, Zhou, Ti and Hu2016; Freethy et al.
Reference Freethy, Conway, Classen, Creely, Happel, Koehn, Vanovac and White2016). An example of the measurement in an ohmic L-mode plasma at DIII-D is shown in figure 11. The wavenumber resolution is determined by the spot-size for the ECE radiometer optics, and the wavenumber response of the reflectometer.
The cross-phase angle between electron density and temperature (the
![]() $n-T$
-phase) does not enter directly into the turbulence-driven flux equations, but the measurement is still extremely valuable because it allows for comparisons at multiple levels of the primacy hierarchy. Nonlinear gyrokinetic simulations can be used to calculate the
$n-T$
-phase) does not enter directly into the turbulence-driven flux equations, but the measurement is still extremely valuable because it allows for comparisons at multiple levels of the primacy hierarchy. Nonlinear gyrokinetic simulations can be used to calculate the
![]() $n-T$
-phase angle, allowing for direct comparisons with experimental measurements. Quasilinear transport models can also be used to calculate the dominant (or subdominant) mode’s cross-phase angle, which means that measurements of the phase angle can be compared against reduced, theory-based transport models (Bourdelle et al.
Reference Bourdelle, Citrin, Baiocchi, Casati, Cottier, Garbet and Imbeaux2016; Staebler et al.
Reference Staebler, Candy, Howard and Holland2016) as well as full nonlinear gyrokinetic models. Linear phase angles tend to track nonlinear phase angles rather well, which makes the phase angle an interesting and robust quantity for comparisons with turbulent-transport models (Dannert & Jenko Reference Dannert and Jenko2005; Waltz, Casati & Staebler Reference Waltz, Casati and Staebler2009; Told et al.
Reference Told, Jenko, Görler, Casson and Fable2013). Comparisons of this measurement with simulations may provide information about the mix of ITG and TEM instabilities in the plasma. For example, the sign of the
$n-T$
-phase angle, allowing for direct comparisons with experimental measurements. Quasilinear transport models can also be used to calculate the dominant (or subdominant) mode’s cross-phase angle, which means that measurements of the phase angle can be compared against reduced, theory-based transport models (Bourdelle et al.
Reference Bourdelle, Citrin, Baiocchi, Casati, Cottier, Garbet and Imbeaux2016; Staebler et al.
Reference Staebler, Candy, Howard and Holland2016) as well as full nonlinear gyrokinetic models. Linear phase angles tend to track nonlinear phase angles rather well, which makes the phase angle an interesting and robust quantity for comparisons with turbulent-transport models (Dannert & Jenko Reference Dannert and Jenko2005; Waltz, Casati & Staebler Reference Waltz, Casati and Staebler2009; Told et al.
Reference Told, Jenko, Görler, Casson and Fable2013). Comparisons of this measurement with simulations may provide information about the mix of ITG and TEM instabilities in the plasma. For example, the sign of the
![]() $n-T$
-phase angle could be used to identify an instability as an ion branch or electron branch mode (Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018), similar to measurements of the propagation direction of turbulence in the plasma frame (Horton Reference Horton1999).
$n-T$
-phase angle could be used to identify an instability as an ion branch or electron branch mode (Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018), similar to measurements of the propagation direction of turbulence in the plasma frame (Horton Reference Horton1999).

Figure 12. (a) The Doppler reflectometer (Doppler backscattering) signal versus time and frequency shows response to changes in rotation associated with neutral beam injection. (b) The mean Doppler shifted frequency (red) is proportional to the phase speed and tracks well the plasma speed measured with charge exchange measurements (CER). Also shown is injected neutral beam power in arbitrary units. From figure 6 of Rhodes et al. (Reference Rhodes, Peebles, Nguyen, Hillesheim, Schmitz, White and Wang2010).
4.4 Doppler reflectometer (Doppler backscattering) diagnostics
Turning to a slightly higher
![]() $k$
measurement, Doppler reflectometers accesses the intermediate range of wavenumbers, with typical ranges
$k$
measurement, Doppler reflectometers accesses the intermediate range of wavenumbers, with typical ranges
![]() $0.5<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<2$
or higher. Doppler reflectometer (DR) (also called Doppler backscattering (DBS)) diagnostics combine the spatial resolution of reflectometry with the wavenumber sensitivity of scattering measurements (Holzhauer et al.
Reference Holzhauer, Hirsch, Grossman, Branaz and Serra1998; Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001; Conway et al.
Reference Conway, Schirmer, Klenge, Suttrop and Holzhauer2004; Hennequin et al.
Reference Hennequin, Honore, Truc, Quemeneur and Lemoine2004; Happel et al.
Reference Happel, Estrade, Blanco, Tribaldos, Cappa and Bustos2009; Hillesheim et al.
Reference Hillesheim, Peebles, Rhodes, Schmitz, Carter, Gourdain and Wang2009; Rhodes 2009; Tokuszawa et al.
Reference Tokuszawa, Ejiri, Kawahata, Tanaka, Yamada, Yoshinuma, Ida and Suzuki2012; Zhou et al.
Reference Zhou, Liu, Zhang, Hu, Wang, Li, Lan, Xie, Sun and Ding2013). Doppler reflectometry is an active measurement. A millimetre-wave beam is launched into a plasma at a frequency that approaches a cutoff (O-mode or X-mode) and at an oblique angle to the cutoff surface. Density fluctuations at particular wavenumber are isolated by choosing frequency of the launched wave, the angle that the launched beam makes with the cutoff surface in the plasmas, and the Bragg scattering. The Bragg condition for
$0.5<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{\text{s}}<2$
or higher. Doppler reflectometer (DR) (also called Doppler backscattering (DBS)) diagnostics combine the spatial resolution of reflectometry with the wavenumber sensitivity of scattering measurements (Holzhauer et al.
Reference Holzhauer, Hirsch, Grossman, Branaz and Serra1998; Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001; Conway et al.
Reference Conway, Schirmer, Klenge, Suttrop and Holzhauer2004; Hennequin et al.
Reference Hennequin, Honore, Truc, Quemeneur and Lemoine2004; Happel et al.
Reference Happel, Estrade, Blanco, Tribaldos, Cappa and Bustos2009; Hillesheim et al.
Reference Hillesheim, Peebles, Rhodes, Schmitz, Carter, Gourdain and Wang2009; Rhodes 2009; Tokuszawa et al.
Reference Tokuszawa, Ejiri, Kawahata, Tanaka, Yamada, Yoshinuma, Ida and Suzuki2012; Zhou et al.
Reference Zhou, Liu, Zhang, Hu, Wang, Li, Lan, Xie, Sun and Ding2013). Doppler reflectometry is an active measurement. A millimetre-wave beam is launched into a plasma at a frequency that approaches a cutoff (O-mode or X-mode) and at an oblique angle to the cutoff surface. Density fluctuations at particular wavenumber are isolated by choosing frequency of the launched wave, the angle that the launched beam makes with the cutoff surface in the plasmas, and the Bragg scattering. The Bragg condition for
![]() $180^{\circ }$
backscattering is given by
$180^{\circ }$
backscattering is given by
![]() $k_{\text{o}}=-2k_{\text{i}}$
, where
$k_{\text{o}}=-2k_{\text{i}}$
, where
![]() $k_{\text{o}}$
is the wavenumber of the measured density fluctuation and
$k_{\text{o}}$
is the wavenumber of the measured density fluctuation and
![]() $k_{\text{i}}$
is the incident wavenumber of the probe beam at the scattering location. By varying the angle of the probe beam with respect to the cutoff layer, the wavenumber
$k_{\text{i}}$
is the incident wavenumber of the probe beam at the scattering location. By varying the angle of the probe beam with respect to the cutoff layer, the wavenumber
![]() $k_{\text{o}}$
is varied. A Doppler reflectometer measurement will yield an autopower spectrum, that looks similar to BES or CECE data in appearance. The frequency spectrum from Doppler reflectometers shows a clear peak at a finite frequency. The location of the peak of the spectrum marks the Doppler-shifted frequency, given by
$k_{\text{o}}$
is varied. A Doppler reflectometer measurement will yield an autopower spectrum, that looks similar to BES or CECE data in appearance. The frequency spectrum from Doppler reflectometers shows a clear peak at a finite frequency. The location of the peak of the spectrum marks the Doppler-shifted frequency, given by
![]() $f_{\text{Dopp}}=f_{\text{plasma}}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k}_{\boldsymbol{o}}$
, where
$f_{\text{Dopp}}=f_{\text{plasma}}+\boldsymbol{v}\boldsymbol{\cdot }\boldsymbol{k}_{\boldsymbol{o}}$
, where
![]() $f_{\text{Dopp}}$
is the frequency of the turbulence in the laboratory frame,
$f_{\text{Dopp}}$
is the frequency of the turbulence in the laboratory frame,
![]() $f_{\text{plasma}}$
is the frequency of the turbulence in the plasma frame,
$f_{\text{plasma}}$
is the frequency of the turbulence in the plasma frame,
![]() $\boldsymbol{v}$
is the phase velocity of the plasma and
$\boldsymbol{v}$
is the phase velocity of the plasma and
![]() $\boldsymbol{k}_{\boldsymbol{o}}$
is the wavenumber of the measured turbulence. Doppler reflectometers are used to measure the phase velocity of the plasma, as shown in figure 12. The location of the peak of the spectrum changes in response to changes in rotation associated with neutral beam injection in this DIII-D plasma.
$\boldsymbol{k}_{\boldsymbol{o}}$
is the wavenumber of the measured turbulence. Doppler reflectometers are used to measure the phase velocity of the plasma, as shown in figure 12. The location of the peak of the spectrum changes in response to changes in rotation associated with neutral beam injection in this DIII-D plasma.
The area under the shifted peak of the measured frequency spectrum is integrated to recover the scattered power at the measured turbulent
![]() $k_{\text{o}}$
. By varying the angle at which the probe beam is launched at the plasma on a shot by shot basis, a Doppler reflectometer can be used to measure a partial wavenumber spectrum of density fluctuations. An example of this is measurement from the TJ-K stellarator is shown in figure 13. The wavenumber spectrum measured at two different radial positions are compared (Fernandez-Marina, Estrada & Blanco Reference Fernandez-Marina, Estrada and Blanco2014).
$k_{\text{o}}$
. By varying the angle at which the probe beam is launched at the plasma on a shot by shot basis, a Doppler reflectometer can be used to measure a partial wavenumber spectrum of density fluctuations. An example of this is measurement from the TJ-K stellarator is shown in figure 13. The wavenumber spectrum measured at two different radial positions are compared (Fernandez-Marina, Estrada & Blanco Reference Fernandez-Marina, Estrada and Blanco2014).

Figure 13. Differences in the wavenumber spectrum measured at two different radial positions in a TJ-K plasma with a Doppler reflectometer are shown. From figure 3 of Fernandez-Marina et al. (Reference Fernandez-Marina, Estrada and Blanco2014)
Doppler reflectometers maximize the wavenumber resolution by minimizing the spread,
![]() $\unicode[STIX]{x0394}k$
, about the probed wavenumber,
$\unicode[STIX]{x0394}k$
, about the probed wavenumber,
![]() $k_{\text{o}}$
(Happel, Blanco & Estrade Reference Happel, Blanco and Estrade2010; Rhodes et al.
Reference Rhodes, Peebles, Nguyen, Hillesheim, Schmitz, White and Wang2010). The wavenumber resolution
$k_{\text{o}}$
(Happel, Blanco & Estrade Reference Happel, Blanco and Estrade2010; Rhodes et al.
Reference Rhodes, Peebles, Nguyen, Hillesheim, Schmitz, White and Wang2010). The wavenumber resolution
![]() $\unicode[STIX]{x0394}k$
can be estimated based on the known width of the probe beam electric field profile, which is selected by the design of the focusing optics, and is typically Gaussian in shape (Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001).
$\unicode[STIX]{x0394}k$
can be estimated based on the known width of the probe beam electric field profile, which is selected by the design of the focusing optics, and is typically Gaussian in shape (Hirsch et al.
Reference Hirsch, Holzhauer, Baldzuhn, Kurzan and Scott2001).
One challenge with scattering measurements, including Doppler reflectometry, is the interpretation of the scattered power amplitude as the density fluctuation amplitude. In most cases, full wave simulations are required to extract absolute density fluctuation levels from reflectometry measurements (Nazikian et al. Reference Nazikian, Kramer and Valeo2001; Conway et al. Reference Conway, Kurzan, Scott, Holzhauer and Kaufmann2002). Given this additional rather extensive modelling requirement, the Doppler reflectometer spectra and fluctuation levels are typically reported in many experiments with arbitrary units, (a.u.), and comparisons with gyrokinetic simulations have primarily focused on the shape of the frequency spectrum measured with a single Doppler reflectometer channel, or the shape of the wavenumber spectrum, constructed from several channels (or several measurement with the same channel, as the probe angle is varied).

Figure 14. From figures 3(b) and 7 of Ruiz Ruiz et al. (Reference Ruiz Ruiz, Ren, Guttenfelder, White, Kaye, Leblanc, Mazzucato, Lee, Domier and Smith2015). (a) Spectra of high-
![]() $k$
density fluctuations from channels 1, 2 and 3 of shot 141767 of the high-
$k$
density fluctuations from channels 1, 2 and 3 of shot 141767 of the high-
![]() $k$
scattering system at NSTX. Each channel measures a different turbulent wavenumber. (b) The multi-channel data is used to construct the wavenumber spectrum of the measured fluctuations at several different times during the discharge, using the same method as that described for multi-channel Doppler reflectometer data analysis.
$k$
scattering system at NSTX. Each channel measures a different turbulent wavenumber. (b) The multi-channel data is used to construct the wavenumber spectrum of the measured fluctuations at several different times during the discharge, using the same method as that described for multi-channel Doppler reflectometer data analysis.
4.5 Coherent scattering
Moving to even higher
![]() $k$
, the electron temperature gradient (ETG) range of wavenumbers, coherent scattering measurements must be used. Diagnostic advances have made it possible to achieve some amount of radial localization diagnostics (Rhodes et al.
Reference Rhodes, Peebles, Van Zeeland, Degrassie, Bravenec, Burrell, DeBoo, Lohr, Petty and Nguyen2007; Smith et al.
Reference Smith, Mazzucator, Lee, Park, Domier and Luhmann2008; Qing et al.
Reference Qing, Junyu, Li, Qingsheng, Yanqing, Tao, Xiaoqi, Bhatti and Xiang2010) but unlike CECE, BES and the Doppler reflectometer, which are naturally radially localized based on their diagnostic principles, coherent scattering is limited to measure fluctuations over a three-dimensional scattering volume, and has poorer spatial resolution than the previously discussed measurement techniques. Noting this limitation, measurement of the wavenumber spectrum is possible, using similar data analysis techniques as Doppler reflectometer: the scattered power spectrum from a single channel gives the spectrum of density fluctuations at a particular wavenumber,
$k$
, the electron temperature gradient (ETG) range of wavenumbers, coherent scattering measurements must be used. Diagnostic advances have made it possible to achieve some amount of radial localization diagnostics (Rhodes et al.
Reference Rhodes, Peebles, Van Zeeland, Degrassie, Bravenec, Burrell, DeBoo, Lohr, Petty and Nguyen2007; Smith et al.
Reference Smith, Mazzucator, Lee, Park, Domier and Luhmann2008; Qing et al.
Reference Qing, Junyu, Li, Qingsheng, Yanqing, Tao, Xiaoqi, Bhatti and Xiang2010) but unlike CECE, BES and the Doppler reflectometer, which are naturally radially localized based on their diagnostic principles, coherent scattering is limited to measure fluctuations over a three-dimensional scattering volume, and has poorer spatial resolution than the previously discussed measurement techniques. Noting this limitation, measurement of the wavenumber spectrum is possible, using similar data analysis techniques as Doppler reflectometer: the scattered power spectrum from a single channel gives the spectrum of density fluctuations at a particular wavenumber,
![]() $k_{\text{o}}$
, with resolution
$k_{\text{o}}$
, with resolution
![]() $\unicode[STIX]{x0394}k$
. In the spectrum, a Doppler shift can be seen, centred at the measured
$\unicode[STIX]{x0394}k$
. In the spectrum, a Doppler shift can be seen, centred at the measured
![]() $k_{\text{o}}$
. By integrating the power spectrum from several channels (several different
$k_{\text{o}}$
. By integrating the power spectrum from several channels (several different
![]() $k_{\text{o}}$
) a partial wavenumber spectrum can be reconstructed. An example is shown from NSTX in figure 14. Three channels are used to measure the frequency spectra at three different wavenumbers, and by integrating the power spectra from each channel over the appropriate frequency range, the three-point wavenumber spectrum is obtained.
$k_{\text{o}}$
) a partial wavenumber spectrum can be reconstructed. An example is shown from NSTX in figure 14. Three channels are used to measure the frequency spectra at three different wavenumbers, and by integrating the power spectra from each channel over the appropriate frequency range, the three-point wavenumber spectrum is obtained.
5 Synthetic diagnostics
None of the fluctuation diagnostics used in fusion plasmas can measure the turbulence in plasma frame perfectly. This imperfection manifests in several ways. First, no turbulence diagnostic can cover the full range of turbulent wavenumbers (the low-
![]() $k$
ITG/TEM range to the intermediate and high-
$k$
ITG/TEM range to the intermediate and high-
![]() $k$
range end for TEM/ETG) using a single measurement technique. Each diagnostic samples the turbulence either at the ion scale, the intermediate scale, or the electron scale. Second, each diagnostic has limited spatial and temporal resolution, so all reported turbulence measurements represent only an average value. The finite spatial extent of the diagnostic’s measurement region is referred to as the ‘sample volume’ or the ‘spot size’. Third, all measurements are made in the laboratory frame – and the plasma is rotating at non-negligible speeds (even without neutral beam injection, intrinsic toroidal rotation can reach substantial Mach numbers many plasmas (Rice Reference Rice2016)). The measured spectra (even the BES and CECE spectra) will include effects of Doppler shifts that must be quantified and understood. Theory predicts that different types of turbulence will have different frequencies and distinct propagation directions depending on the type of turbulence (Horton Reference Horton1999). This means it is highly desired, but generally very difficult, to extract the plasma-frame spectrum of the turbulence from measurements. Because a dominant Doppler shift typically determines the shape of the measured spectrum, one must proceed with extreme caution when trying to identify the turbulence based on the laboratory-frame frequency spectrum.
$k$
range end for TEM/ETG) using a single measurement technique. Each diagnostic samples the turbulence either at the ion scale, the intermediate scale, or the electron scale. Second, each diagnostic has limited spatial and temporal resolution, so all reported turbulence measurements represent only an average value. The finite spatial extent of the diagnostic’s measurement region is referred to as the ‘sample volume’ or the ‘spot size’. Third, all measurements are made in the laboratory frame – and the plasma is rotating at non-negligible speeds (even without neutral beam injection, intrinsic toroidal rotation can reach substantial Mach numbers many plasmas (Rice Reference Rice2016)). The measured spectra (even the BES and CECE spectra) will include effects of Doppler shifts that must be quantified and understood. Theory predicts that different types of turbulence will have different frequencies and distinct propagation directions depending on the type of turbulence (Horton Reference Horton1999). This means it is highly desired, but generally very difficult, to extract the plasma-frame spectrum of the turbulence from measurements. Because a dominant Doppler shift typically determines the shape of the measured spectrum, one must proceed with extreme caution when trying to identify the turbulence based on the laboratory-frame frequency spectrum.
In order to take all these effects into account, one can model the diagnostic response and attempt to unfold how the actual turbulence spectrum would appear in a gyrokinetic simulation (in the plasma frame), given the measurement’s limitations. One example of this approach is found in Shafer et al. (Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012). It is more common to proceed in the opposite direction: model the diagnostic response and apply the model to the output of a gyrokinetic simulation in order to generate ‘synthetic diagnostic data’ representative of the laboratory-frame measurements, and then, compare this synthetic data to the actual data from the experiment.
5.1 Fundamental principles of synthetic diagnostics
One of the first general descriptions of the effects of the sample volume on turbulence measurements was presented by Bravenec & Wootton (Reference Bravenec and Wootton1995). Because diagnostics such as heavy-ion beam probe (HIBP), beam-emission spectroscopy (BES), correlation electron cyclotron emission (CECE) radiometers and even Langmuir probes, will sample turbulence in a finite volume of space, the measurements will average over shorter-wavelength components of the turbulence. The result is that the measured power spectrum, fluctuation amplitude and correlation lengths will all depend on the size of the sample volume.

Figure 15. From figure 1 of Bravenec & Wootton (Reference Bravenec and Wootton1995). A sketch illustrating sample volume attenuation of a plane wave of wavelength A. The shaded regions of length
![]() $d_{a}$
and
$d_{a}$
and
![]() $d_{b}$
represent 1-D sharp boundaries of the sample volumes or spot sizes.
$d_{b}$
represent 1-D sharp boundaries of the sample volumes or spot sizes.
Figure 15 shows the effect of spatial averaging on the measurement of a coherent sine wave perturbation and how this is related to wavenumber averaging. If the spot size is less than the wavelength, then the perturbation can be measured, but if the spot size is equal to the wavelength, the peak and trough cancel each other out and the perturbation is not measured. A simple expression, relevant for measurements like BES and CECE, gives the maximum measureable wavenumber as
![]() $k_{\text{max}}=2\unicode[STIX]{x03C0}/d$
, where
$k_{\text{max}}=2\unicode[STIX]{x03C0}/d$
, where
![]() $d$
is the diameter of the spot size (Bravenec & Wootton Reference Bravenec and Wootton1995).
$d$
is the diameter of the spot size (Bravenec & Wootton Reference Bravenec and Wootton1995).

Figure 16. (a) Shows the output fluctuations of an ion-scale nonlinear gyrokinetic simulation, mapped from the simulation geometry to real-space geometry in the
![]() $R$
and
$R$
and
![]() $Z$
plane. The white contour marks the spot size and measurement location a channel from a turbulence diagnostic. (b) The simulated time histories of the fluctuations generated at the centre of the white contours, which mimics the laboratory-frame measurement by including the Doppler shift effects with (red) and without (black) the finite sample volume filter applied.
$Z$
plane. The white contour marks the spot size and measurement location a channel from a turbulence diagnostic. (b) The simulated time histories of the fluctuations generated at the centre of the white contours, which mimics the laboratory-frame measurement by including the Doppler shift effects with (red) and without (black) the finite sample volume filter applied.
The numerical implementation steps required to generate synthetic diagnostics for BES and CECE measurements for the gyrokinetic code GYRO are described in Holland et al. (Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009), with results illustrated in figure 16. Figure 16(a) shows the output fluctuations of an ion-scale nonlinear gyrokinetic simulation, which have been mapped from the simulation geometry to real-space geometry in the
![]() $R$
and
$R$
and
![]() $Z$
plane, where
$Z$
plane, where
![]() $R$
is the major radius of the plasma and
$R$
is the major radius of the plasma and
![]() $Z$
is the position above the outboard midplane of the tokamak. The white contour marks the spot size and measurement location of one channel of each the CECE and BES diagnostics. A simulated time history of the fluctuations has been generated from the simulation output at the centre of the white contours, without the spatial filtering, is shown in black in figure 16(b). The synthetic model includes the Doppler shift effects. After the spatial averaging is applied, the fluctuations within the white contour sample volume are averaged to give the filtered time history (red). The effect of the spatial averaging translates into a low-pass filter on the Doppler-shifted fluctuating synthetic time series, as well as a low-pass filter in
$Z$
is the position above the outboard midplane of the tokamak. The white contour marks the spot size and measurement location of one channel of each the CECE and BES diagnostics. A simulated time history of the fluctuations has been generated from the simulation output at the centre of the white contours, without the spatial filtering, is shown in black in figure 16(b). The synthetic model includes the Doppler shift effects. After the spatial averaging is applied, the fluctuations within the white contour sample volume are averaged to give the filtered time history (red). The effect of the spatial averaging translates into a low-pass filter on the Doppler-shifted fluctuating synthetic time series, as well as a low-pass filter in
![]() $k$
-space, as discussed previously (Bravenec & Wootton Reference Bravenec and Wootton1995).
$k$
-space, as discussed previously (Bravenec & Wootton Reference Bravenec and Wootton1995).
5.2 General effects of applying synthetic diagnostics to gyrokinetic simulation outputs
Ultimately, every synthetic turbulence diagnostic must account for the limited spatial and wavenumber sensitivity of the actual measurements.
Using results from BES synthetic diagnostic, several general examples of how a synthetic diagnostic modifies the raw turbulence predicted by a gyrokinetic code can be described. First, applying a synthetic diagnostic will generally lead to a reduction of fluctuation amplitude and an increase in radial correlation length, compared to unfiltered gyrokinetic simulation outputs.

Figure 17. Figure shows the reduction in amplitude of the power spectrum (a) and the increase in correlation length (b) due to finite sample volume effects for BES measurements at mid-radius in DIII-D. Panel (a) from figure 7(a) and (b) from figure 12(a) of Holland et al. (Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009).
Figure 17(a) demonstrates such effects. The reduction in fluctuation amplitude can be seen in the difference between the unfiltered power spectra and filtered power spectra in figure 17(a), because the r.m.s. fluctuation amplitude is related directly to the area under the curve. The unfiltered power spectrum output by the simulation contains contributions from all simulated wavenumbers and frequencies. The red curve is the power spectrum after application of the synthetic diagnostics. The synthetic diagnostic has filtered the fluctuations, to extract only the measured wavenumber and frequency ranges. This leads to a signal with a reduced r.m.s. fluctuation level, and the reduced spectrum as shown in figure 17(a). The experimental spectrum is shown in blue. The effects of the Doppler shift to set the peak and width of the measured spectrum and the averaging effects of spot size to set the amplitude are needed in the synthetic diagnostic model in order to directly compare the BES power spectrum to a gyrokinetic simulation.
Figure 17(b) shows the effect of the synthetic diagnostic on the correlation length. Because the synthetic diagnostic is acting as a low-pass filter in
![]() $k$
-space, it attenuates the higher
$k$
-space, it attenuates the higher
![]() $k$
(longer wavelength) contributions. Also, in this case, it causes the measurement volumes to overlap. The overall effect is an increase in the correlation length after the synthetic diagnostic is applied. This effect must be taken into account to compare the simulation output quantitatively with the measurements.
$k$
(longer wavelength) contributions. Also, in this case, it causes the measurement volumes to overlap. The overall effect is an increase in the correlation length after the synthetic diagnostic is applied. This effect must be taken into account to compare the simulation output quantitatively with the measurements.
In addition to general effects, each measurement technique will require a specialized synthetic diagnostic model, which will be dependent on fundamental measurement principles and practical implementation. For example, with BES and CECE the wavenumber sensitivity is directly linked to the spot size or sample volume (Bravenec & Wootton Reference Bravenec and Wootton1995; Holland et al. Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Shafer et al. Reference Shafer, Fonck, McKee, Holland, White and Schlossberg2012).

Figure 18. From figure 16 of Ernst et al. (Reference Ernst, Burrell, Guttenfelder, Rhodes, Dimits, Bravenec, Grierson, Holland, Lohr and Marinoni2016). The frequency spectra measured at one wavenumber at two different times in a discharge with Doppler backscattering (DBS) at DIII-D are compared to GYRO results by applying a synthetic diagnostic.
Synthetic diagnostics for Doppler reflectometers have been implemented for several codes, including the flux-driven code ELMFIRE (Leerink et al.
Reference Leerink, Bulanin, Gusakov, Heikkinen, Janhumen, Kiviniemi, Korpilo, Nora and Ogando2010), and the gradient-driven code GYRO (Ernst et al.
Reference Ernst, Burrell, Guttenfelder, Rhodes, Dimits, Bravenec, Grierson, Holland, Lohr and Marinoni2016), with an example comparing a synthetic spectrum from the GYRO code to an experimental spectrum from DIII-D is shown in figure 18 (Ernst et al.
Reference Ernst, Burrell, Guttenfelder, Rhodes, Dimits, Bravenec, Grierson, Holland, Lohr and Marinoni2016). Synthetic diagnostics for high-
![]() $k$
coherent scattering measurements have been implemented in GTS (Poli et al.
Reference Poli, Ethier, Wang, Hahm, Mazzucato and Smith2010). In the case of Doppler reflectometry measurements, calculation of the wavenumber response and sample volume size is more complicated recent work has focused on advanced synthetic diagnostic modelling that involves full wave simulations of the reflectometer–plasma interactions (Hacquin et al.
Reference Hacquin, Citrin, Arnichand, Sabot, Bourdelle, Garbet and Kramer-Flecken2016; Happel et al.
Reference Happel, Görler, Hennequin, Lechte, Bernert, Conway, Freethy, Honore, Pinson and Stroth2017).
$k$
coherent scattering measurements have been implemented in GTS (Poli et al.
Reference Poli, Ethier, Wang, Hahm, Mazzucato and Smith2010). In the case of Doppler reflectometry measurements, calculation of the wavenumber response and sample volume size is more complicated recent work has focused on advanced synthetic diagnostic modelling that involves full wave simulations of the reflectometer–plasma interactions (Hacquin et al.
Reference Hacquin, Citrin, Arnichand, Sabot, Bourdelle, Garbet and Kramer-Flecken2016; Happel et al.
Reference Happel, Görler, Hennequin, Lechte, Bernert, Conway, Freethy, Honore, Pinson and Stroth2017).
5.3 Practical considerations for synthetic diagnostics
All of the synthetic diagnostics described above are applied during post-processing, i.e. the gyrokinetic code outputs are used to create synthetic time series, and then these time series can be analysed using the exact same analysis techniques as applied to the experimental time series. This has the advantage of allowing a very direct comparison with experiment by using identical analysis routines. However, there are practical challenges to this direct approach. This approach requires fluctuation outputs from the codes at enough spatial and temporal points to reconstruct a time history of the fluctuations in real space
![]() $(R,Z)$
. This means that the fluctuations from the code must be output at frequent enough time internals to avoid aliasing in frequency space (i.e. the Nyquist frequency of the synthetic time series must be high enough). In addition, the data in real space must be output over a large enough spatial region (simulation box size) and on a fine enough spatial grid to avoid aliasing in
$(R,Z)$
. This means that the fluctuations from the code must be output at frequent enough time internals to avoid aliasing in frequency space (i.e. the Nyquist frequency of the synthetic time series must be high enough). In addition, the data in real space must be output over a large enough spatial region (simulation box size) and on a fine enough spatial grid to avoid aliasing in
![]() $k$
-space (Holland et al.
Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Görler et al.
Reference Görler, White, Told, Jenko, Holland and Rhodes2014). These requirements result in very large output files from the gyrokinetic simulations, easily exceeding tens of GB, and approaching TBs in some cases. Ideas for in situ synthetic diagnostics are under development, but these are not yet widely available. It is also important to keep in mind that any synthetic diagnostic is fundamentally another model that must be tested, verified and validated independently – ideally before being used with a gyrokinetic code to compare with experiments.
$k$
-space (Holland et al.
Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; Görler et al.
Reference Görler, White, Told, Jenko, Holland and Rhodes2014). These requirements result in very large output files from the gyrokinetic simulations, easily exceeding tens of GB, and approaching TBs in some cases. Ideas for in situ synthetic diagnostics are under development, but these are not yet widely available. It is also important to keep in mind that any synthetic diagnostic is fundamentally another model that must be tested, verified and validated independently – ideally before being used with a gyrokinetic code to compare with experiments.
6 Frontiers in gyrokinetic transport model validation
At the frontiers of validation of turbulent transport in fusion plasmas, a growing number of researchers are actively deploying high-performance computing resources for massive simulations of unprecedented physics fidelity. They are also leveraging reduced models in innovative ways using advanced algorithms, artificial intelligence and machine learning; and are pushing the envelope of predictive experimental design initiatives, potentially finding a way to control and optimize turbulent transport. The standard models of drift-wave turbulent transport are being extended to include the interactions between MHD modes and turbulence (McDevitt & Diamond Reference McDevitt and Diamond2006; Militello et al. Reference Militello, Waelbroeck, Fitzpatrick and Horton2008; Bañón Navarro et al. Reference Bañón Navarro, Bardóczi, Carter, Jenko and Rhodes2017) and the interactions between fast ion modes and turbulence (Estrada Mila et al. Reference Estrada Mila, Candy and Waltz2006; Pueschel et al. Reference Pueschel, Jenko, Schneller, Hauff, Gunter and Tardini2012; Wilkie et al. Reference Wilkie, Abel, Landreman and Dorland2016). Most exciting perhaps, there are experimental observations that can be viewed as grand challenges to the standard turbulent-transport models, including intrinsic rotation and intrinsic rotation reversals (Parra & Barnes Reference Parra and Barnes2015; Rice Reference Rice2016), momentum transport (Diamond et al. Reference Diamond, Kosuga, Gürcan, Mcdevitt, Hahm, Fedorczak, Rice, Wang, Ku and Kwon2013) and ‘non-local’ perturbative transport phenomena (Ida et al. Reference Ida, Shi, Sun, Inagaki, Kamiya, Rice, Tamura, Diamond, Dif-Pradalier and Zou2015; Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, White, Howard, Grierson, Staebler, Rice, Yuan, Cao, Greenwald and Hubbard2018a ). These areas are described briefly in the next four subsections.
6.1 Global effects and flux-driven simulations
The potential impact of ‘global effects’ on turbulent transport is a frontier area to be explored. Global effects are sometimes also called ‘non-local’ effects or ‘meso-scale’ effects. The study of global or non-local effects, such as turbulence spreading or long-range correlations and avalanche type events can be assessed using global, flux-driven simulations (Garbet Reference Garbet2010). It is not possible to provide a full description of this very diverse area of study, even within the limited context of gyrokinetic model validation. Two review articles on ‘non-local’ phenomena in fusion plasmas are Callen & Kissick (Reference Callen and Kissick1997), Ida et al. (Reference Ida, Shi, Sun, Inagaki, Kamiya, Rice, Tamura, Diamond, Dif-Pradalier and Zou2015).
In a flux-driven simulation, where background profiles are evolved along with the turbulence, the validation workflow example described in § 3 is modified. Instead of pressure profiles being used as an input to the code, the heat fluxes are used as an input. The flux-driven simulation then calculates the pressure profiles (due to turbulent transport) and these can be compared with the experiment. Examples of a full-
![]() $f$
, global gyrokinetic codes run with a flux-driven workflow and compared with turbulence measurements include references (Leerink et al.
Reference Leerink, Bulanin, Gusakov, Heikkinen, Janhumen, Kiviniemi, Korpilo, Nora and Ogando2010; Dif-Pradalier et al.
Reference Dif-Pradalier, Hornung, Ghendrih, Sarazin, Clairet, Vermare, Diamond, Abiteboul and Cartier-Michaud2015; Grandgirard et al.
Reference Grandgirard, Abiteboul, Bigot, Cartier-Michaud, Crouseilles, Dif-Pradalier, Ehrlacher, Esteve, Garbet and Ghendrih2016). Flux-driven simulations can be performed with
$f$
, global gyrokinetic codes run with a flux-driven workflow and compared with turbulence measurements include references (Leerink et al.
Reference Leerink, Bulanin, Gusakov, Heikkinen, Janhumen, Kiviniemi, Korpilo, Nora and Ogando2010; Dif-Pradalier et al.
Reference Dif-Pradalier, Hornung, Ghendrih, Sarazin, Clairet, Vermare, Diamond, Abiteboul and Cartier-Michaud2015; Grandgirard et al.
Reference Grandgirard, Abiteboul, Bigot, Cartier-Michaud, Crouseilles, Dif-Pradalier, Ehrlacher, Esteve, Garbet and Ghendrih2016). Flux-driven simulations can be performed with
![]() $\unicode[STIX]{x2202}f$
codes as well. This is done by coupling local gyrokinetic simulations (e.g. flux-tube simulations) to a transport solver. Two examples of this approach are the TRINITY framework (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammet and Jenko2010) and the TGYRO framework (Candy et al.
Reference Candy, Holland, Waltz, Fahey and Belli2009).
$\unicode[STIX]{x2202}f$
codes as well. This is done by coupling local gyrokinetic simulations (e.g. flux-tube simulations) to a transport solver. Two examples of this approach are the TRINITY framework (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammet and Jenko2010) and the TGYRO framework (Candy et al.
Reference Candy, Holland, Waltz, Fahey and Belli2009).
It has been suggested that using flux-driven simulations might eliminate some of the complications with extreme sensitivity to inputs used in simulations. A flux-driven simulation uses the experimental fluxes as inputs, so the results will still naturally be sensitive to errors and uncertainties on the inputs (in this case, the input fluxes). The experimentally inferred fluxes depend on the models and measurements used to ascertain the sources and sinks. As described in § 3, the sources and sinks used to calculate the experimental fluxes using power balance code are not without uncertainty. Hence the inputs to the flux-driven simulation will have (sometimes large) error bars and uncertainty, just as inputs to a gradient-driven simulation have (sometimes large) error bars and uncertainties. It would still be necessary to deploy a validation methodology to enable comparison with experiment, which would include extensive sensitivity scans of input parameters within experimental error bars. This can become prohibitively expensive when running a global gyrokinetic simulation, where the equilibrium profiles and fluctuations are solved for self-consistently. This is one practical reason why to date very few validation studies have been carried out with global gyrokinetic codes, making this area an exciting frontier.
6.2 Predictive experimental design: the predict first initiative
Nonlinear gyrokinetic simulations are usually run after an experiment. In a few cases, they have been run prior to an experiment, in order to design and predict what would be measured. The example discussed in § 6.3 shows how using outputs from a multi-scale simulation to predict changes in turbulence before measuring them in an experiment and is one example of the ‘predict first’ initiative, or predictive experimental design (Mantica et al.
Reference Mantica, Bourdelle, Camenen, Dejarnac, Evans, Görler, Hillesheim, Idomura, Jakubowski and Ricci2017). Documenting code predictions in advance is one additional validation ‘best practice’ (Greenwald Reference Greenwald2010), but can be challenging to do with nonlinear gyrokinetic simulations from a practical perspective. Progress has been made by careful coordination among experiment and theory groups to save and analyse turbulence outputs from simulations that were run for past validation experiments. These outputs can be used before new experiments to select discharge parameters of interest; and the computing resources serve double duty for both interpretation and prediction. This was done in the case of
![]() $n-T$
-phase angle predictions at DIII-D and AUG (White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
; Bañón Navarro et al.
Reference Bañón Navarro, Happel, Görler, Jenko, Abiteboul, Bustos, Doerk and Told2015; Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018). An example combining the predict first frontier and simulation of global effects comes from TORESUPRA, where flux-driven, global gyrokinetic simulations have been used to predict the occurrence of so-called ‘meso-scale’ phenomena prior to experimental observations Dif-Pradalier et al.
Reference Dif-Pradalier, Hornung, Ghendrih, Sarazin, Clairet, Vermare, Diamond, Abiteboul and Cartier-Michaud2015. Predict first approaches have also been used to provide constraints on hardware designs for new turbulence measurements at C-Mod (White et al.
Reference White, Howard, Mikkelsen, Greenwald, Candy and Waltz2011). In addition, nonlinear gyrokinetic simulations have been used to predict turbulence characteristics in the W7-X stellarator years before first plasma operation (Xanthopoulos et al.
Reference Xanthopoulos, Merz, Görler and Jenko2007). Controlling and optimizing turbulent transport in stellarators have even been suggested (Xanthopoulos et al.
Reference Xanthopoulos, Mynick, Helander, Turkin, Plunk, Jenko, Görler, Told, Bird and Proll2016). It is notable that W7-X has already several turbulence diagnostics (PCI, CECE, etc.), available in the first experimental campaigns.
$n-T$
-phase angle predictions at DIII-D and AUG (White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
; Bañón Navarro et al.
Reference Bañón Navarro, Happel, Görler, Jenko, Abiteboul, Bustos, Doerk and Told2015; Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018). An example combining the predict first frontier and simulation of global effects comes from TORESUPRA, where flux-driven, global gyrokinetic simulations have been used to predict the occurrence of so-called ‘meso-scale’ phenomena prior to experimental observations Dif-Pradalier et al.
Reference Dif-Pradalier, Hornung, Ghendrih, Sarazin, Clairet, Vermare, Diamond, Abiteboul and Cartier-Michaud2015. Predict first approaches have also been used to provide constraints on hardware designs for new turbulence measurements at C-Mod (White et al.
Reference White, Howard, Mikkelsen, Greenwald, Candy and Waltz2011). In addition, nonlinear gyrokinetic simulations have been used to predict turbulence characteristics in the W7-X stellarator years before first plasma operation (Xanthopoulos et al.
Reference Xanthopoulos, Merz, Görler and Jenko2007). Controlling and optimizing turbulent transport in stellarators have even been suggested (Xanthopoulos et al.
Reference Xanthopoulos, Mynick, Helander, Turkin, Plunk, Jenko, Görler, Told, Bird and Proll2016). It is notable that W7-X has already several turbulence diagnostics (PCI, CECE, etc.), available in the first experimental campaigns.
6.3 Challenges of validating multi-scale gyrokinetic simulations
Most gyrokinetic simulations to date exploit the large spatio-temporal scale separation between the ITG and ETG turbulence. This allows one to run single-scale simulations, where either the long wavelength turbulence or the short-wavelength turbulence is simulated. In many cases, high physics fidelity single-scale simulations have been able to reproduce within error bars the measured turbulence characteristics and inferred heat fluxes from power balance calculations in a variety of plasmas across many machines (White et al.
Reference White, Schmitz, McKee, Holland, Peebles, Carter, Shafer, Austin, Burrell and Candy2008; Casati et al.
Reference Casati, Gerbaud, Hennequin, Bourdelle, Candy, Clairet, Garbet, Grandgirard, Gurcan and Heuraux2009; Holland et al.
Reference Holland, White, McKee, Shafer, Candy, Waltz, Schmitz and Tynan2009; White et al.
Reference White, Peebles, Rhodes, Holland, Wang, Schmitz, Carter, Hillesheim, Doyle and Zeng2010a
; Holland et al.
Reference Holland, Petty, Schmitz, Burrell, McKee, Rhodes and Candy2012 (H-mode); Howard et al.
Reference Howard, White, Reinke, Greenwald, Holland, Candy and Walk2013; Told et al.
Reference Told, Jenko, Görler, Casson and Fable2013; Field et al.
Reference Field, Dunai, Ghim, Hill, McMillan, Roach, Saarelma, Schekochihin and Zoletnik2014; Görler et al.
Reference Görler, White, Told, Jenko, Holland and Rhodes2014; White et al.
Reference White, Howard, Creely, Chilenski, Greenwald, Hubbard, Hughes, Marmar, Rice and Sierchio2015; Sung et al.
Reference Sung, White, Mikkelsen, Greenwald, Holland, Howard, Churchill and Theiler2016; Creely et al.
Reference Creely, Howard, Rodriguez-Fernandez, Cao, Hubbard, Hughes, Rice, White, Candy and Staebler2017, van Wyk et al.
Reference van Wyk, Highcock, Field, Roach, Schekochihin, Parra and Dorland2017; Freethy et al.
Reference Freethy, Görler, Creely, Conway, Happel and White2018). In addition, single-scale (ion-scale) simulations can also match measured impurity transport within error bars (Howard et al.
Reference Howard, Greenwald, Mikkelsen, Reinke, White, Ernst, Podpaly and Candy2012). Within the last several years, it was found that certain plasmas could not be well described by single-scale gyrokinetic simulations. This led to the pursuit of realistic mass
![]() $(m_{\text{i}}/m_{\text{e}}=3600)$
multi-scale simulations, which include a range of wavenumbers encompassing ITG/TEM as well as ETG simultaneously (Howard et al.
Reference Howard, Holland, White, Greenwald and Candy2014, Reference Howard, Holland, White, Greenwald, Candy and Creely2016; Howard 2017; Holland, Howard & Grierson Reference Holland, Howard and Grierson2017; Howard et al.
Reference Howard, Holland, White, Greenwald, Rodriguez-Fernandez, Candy and Creely2018). Multi-scale simulations are extremely computationally expensive, and only a handful have been performed to model real experimental discharges. Experimentally realistic multi-scale simulations performed for C-Mod plasmas show expected increases in electron heat flux compared to an ion-scale simulation (contributions from the ETG turbulence). The simulations also found an increase in ion heat flux due to cross-scale interactions, which was not expected (Howard et al.
Reference Howard, Holland, White, Greenwald and Candy2014). Cross-scale coupling between ion-scale turbulence and electron-scale turbulence is also seen in Cyclone Base Case simulations (Maeyama et al.
Reference Maeyama, Idomura, Wantanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015); similar enhancements of low-
$(m_{\text{i}}/m_{\text{e}}=3600)$
multi-scale simulations, which include a range of wavenumbers encompassing ITG/TEM as well as ETG simultaneously (Howard et al.
Reference Howard, Holland, White, Greenwald and Candy2014, Reference Howard, Holland, White, Greenwald, Candy and Creely2016; Howard 2017; Holland, Howard & Grierson Reference Holland, Howard and Grierson2017; Howard et al.
Reference Howard, Holland, White, Greenwald, Rodriguez-Fernandez, Candy and Creely2018). Multi-scale simulations are extremely computationally expensive, and only a handful have been performed to model real experimental discharges. Experimentally realistic multi-scale simulations performed for C-Mod plasmas show expected increases in electron heat flux compared to an ion-scale simulation (contributions from the ETG turbulence). The simulations also found an increase in ion heat flux due to cross-scale interactions, which was not expected (Howard et al.
Reference Howard, Holland, White, Greenwald and Candy2014). Cross-scale coupling between ion-scale turbulence and electron-scale turbulence is also seen in Cyclone Base Case simulations (Maeyama et al.
Reference Maeyama, Idomura, Wantanabe, Nakata, Yagi, Miyato, Ishizawa and Nunami2015); similar enhancements of low-
![]() $k$
heat flux were found.
$k$
heat flux were found.

Figure 19. From figure 10 Howard et al. (Reference Howard, Holland, White, Greenwald, Candy and Creely2016). The power spectrum of the density fluctuations is predicted using multi-scale simulations with different values of
![]() $a/LTi$
. The predicted ‘flattening’ of the spectrum between
$a/LTi$
. The predicted ‘flattening’ of the spectrum between
![]() $1<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{s}<5$
(red) compared to the other two cases (black and blue) can be tested experimentally.
$1<k_{\unicode[STIX]{x1D703}}\unicode[STIX]{x1D70C}_{s}<5$
(red) compared to the other two cases (black and blue) can be tested experimentally.
These new physics predictions must be tested by comparing multi-scale simulations with experimental fluctuation measurements. But multi-scale simulations pose several practical challenges for validation. A set of nonlinear ion-scale gyrokinetic simulations used in a typical validation study (including all sensitivity scans) may require up to 5 M CPU hours of computing time. In contrast, a set of nonlinear multi-scale gyrokinetic simulations may require over 100 M CPU hours for all the scans needed to compare with the experiment. There is a need to leverage fluctuation measurements in new experiments to test existing predictions from multi-scale simulations, because it may be more difficult to run new simulations than to perform new experiments in these cases. In one example of interest, changes in turbulence are predicted in multi-scale simulations that are not seen in ion-scale simulations: the wavenumber spectrum of the intermediate-
![]() $k$
turbulence flattens as the
$k$
turbulence flattens as the
![]() $a/L_{\text{Ti}}$
drive is increased, see figure 19 reproduced from Howard et al. (Reference Howard, Holland, White, Greenwald, Candy and Creely2016). These predictions may be tested using Doppler reflectometer to measure the predicted flattening of the wavenumber spectrum at intermediate wavenumbers in future experiments. This type of approach is part of a ‘predict first’ initiative in the community, and is discussed more in the next section.
$a/L_{\text{Ti}}$
drive is increased, see figure 19 reproduced from Howard et al. (Reference Howard, Holland, White, Greenwald, Candy and Creely2016). These predictions may be tested using Doppler reflectometer to measure the predicted flattening of the wavenumber spectrum at intermediate wavenumbers in future experiments. This type of approach is part of a ‘predict first’ initiative in the community, and is discussed more in the next section.
6.4 Leveraging reduced models and advanced algorithms
The detailed predictions for turbulence described in the previous section are extremely valuable to probing the underlying physics of turbulent transport. However, many predictions of interest for designing new fusion devices do not need high-fidelity gyrokinetic models. Thinking now as engineers – we imagine wanting to be able to run reduced models instead of a full physics nonlinear gyrokinetic model to predict experimental performance. Low-fidelity, approximate models are good enough for engineering design and optimization in many cases. Different goals in the areas of physics and engineering are deeply connected in fusion energy research. The validation effort surrounding nonlinear gyrokinetic codes helps to develop deeper physics understanding, and leads to improved reduced models. In a recent demonstration of this, the physics of cross-scale coupling learned from multi-scale GYRO simulations was adopted and implemented in a new reduced TGLF model (Staebler et al. Reference Staebler, Candy, Howard and Holland2016).
The reduced models are incomplete by design, but are efficient to use. This efficiency has been recently pushed to new extremes. Reduced models can now leverage new developments in big data science, machine learning and artificial intelligence, such as deep learning algorithms. For example, ‘trained’ transport models based on neural network techniques have been developed using the reduced transport models TGLF (Meneghini et al. Reference Meneghini, Smith, Snyder, Staebler, Candy, Belli, Lao, Kostuk, Luce and Luda2017) and QuaLiKiz (Citrin et al. Reference Citrin, Breton, Felici, Imbeaux, Aniel, Artaud, Baiocchi, Bourdelle, Camenen and Garcia2015), using compiled databases of transport model outputs. Both ‘trained’ models are faster than TGLF and QuaLiKiz respectively, and could be used to predict experimental transport, potentially in real time. Leveraging advanced algorithms is not limited to big data sets. Applying improved optimization techniques to reduced models is one way to probe which model is most correct, and to determine – possibly before a multi-scale gyrokinetic simulation is run – whether that expensive simulation is needed to explain the experimental observations. A new optimization routine, built around TGLF (Rodriguez-Fernandez et al. Reference Rodriguez-Fernandez, White, Creely, Greenwald, Howard, Sciortino and Wright2018b ) can also help find which of many drive terms are most important to match the experimental heat fluxes within error bars. Once a set of inputs is identified, one could go back and run nonlinear simulations as needed to verify these cases. Hence this tool can be used as a guide for future, targeted nonlinear gyrokinetic validation studies.
7 Discussion and outlook
This article has explored validation of nonlinear gyrokinetic simulations using direct comparisons with measured turbulence in fusion plasmas within a well-established and rigorous methodology. The community-wide effort described here is very much an exercise in physics. Accepting validation of nonlinear turbulence models as a physics research tool is a familiar concept in the domain of fluid mechanics (Moin & Krishnan Reference Moin and Krishnan1998). But the concept can seem foreign in the broader fusion community, where a great deal of emphasis is naturally placed on predicting fusion performance. This makes sense, of course, because the ultimate purpose of fusion energy research is to develop a working fusion reactor. When that is the goal, any model that agrees with experiments will do, regardless of the physics contained in the model. For example, the
![]() $H_{98y2}$
parameter is the thermal energy confinement time normalized to an empirically predicted confinement time; the latter comes from a scaling relation developed from a multi-tokamak database of ELMing H-mode plasmas. The
$H_{98y2}$
parameter is the thermal energy confinement time normalized to an empirically predicted confinement time; the latter comes from a scaling relation developed from a multi-tokamak database of ELMing H-mode plasmas. The
![]() $H_{98y2}$
parameter is more widely used than any theory-based model for predicting performance in tokamaks, and it was used to design ITER (ITER 1999).
$H_{98y2}$
parameter is more widely used than any theory-based model for predicting performance in tokamaks, and it was used to design ITER (ITER 1999).
The very close connection between seeking a deeper understanding of turbulent transport in fusion plasmas and the development of predictive capabilities makes transport model validation a rich area of fusion research. It is very natural and correct to view validation of nonlinear gyrokinetic turbulent-transport models as an exercise in the scientific method. Careful comparison between experiment and theory are carried out, ultimately to gain a deeper understanding of the fundamental physical processes of interest. The nonlinear gyrokinetic equations used to describe turbulence in fusion plasmas must be solved numerically, and this creates many challenges, and also many opportunities, to study turbulence. Using validation of gyrokinetic transport models as a research tool creates new opportunities to study plasma turbulence with unprecedented detail. And in fusion research, the connection between validation for physics goals and engineering goals can be quite direct. Guided by advances in understanding the turbulence in fusion plasmas, reduced physics turbulent-transport models are actively being developed with the goal of predicting pressure profiles and fusion performance in ITER (Kinsey et al. Reference Kinsey, Staebler, Candy, Waltz and Budny2011). These reduced models will become part of integrated simulation frameworks, which will enable whole device modelling (Bonoli & McInnes Reference Bonoli and McInnes2015).
As the theoretical framework for understanding transport in fusion plasmas advances, comparing new models, or extensions of the standard models, to experimental results via rigorous validation methodology will become increasingly important. Current fusion devices are quite well diagnosed, and new measurements are coming online in every campaign. Major tokamaks and stellarators around the world, as well as small-to-medium scale fusion and basic plasma experiments, can all become excellent platforms for validation-oriented research with enough investment in diagnostics and modelling efforts. Validation research in the fusion community is vibrant and will continue to expand, with efforts dedicated to advancing predictive capability and to advancing fundamental physics understanding in support of ITER and other future burning plasma experiments.
Acknowledgements
The author is very grateful to their collaborators T. Goerler, M. Greenwald, W. Guttenfelder and C. Holland, for many years of vigorous discussion about validation of GK codes using turbulence measurements, and for sharing their wisdom on this topic. The author is also indebted to the referees and to A. J. Creely, N. T. Howard, J. Rice, P. Rodriguez Fernandez, F. Sciortino and J. Ruiz Ruiz for many critical comments and insightful suggestions that have greatly improved this article.