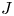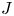1. Introduction
The Wendelstein 7-X (W7-X) optimised stellarator (Beidler et al. Reference Beidler, Grieger, Herrnegger, Harmeyer, Kisslinger, Lotz, Maassberg, Merkel, Nührenberg, Rau, Sapper, Sardei, Scardovelli, Schlüter and Wobig1990) has helped give rise to a renaissance of the stellarator fusion concept. The optimisation of the magnetic geometry of W7-X to reduce neoclassical transport via quasi-isodynamicity has yielded performance comparable to that of a similar tokamak (Dinklage et al. Reference Dinklage2018). This optimisation has led to turbulent transport becoming the predominant cause of unwanted heat and particle losses. Turbulent transport arises as a consequence of the inevitable temperature and density gradients in fusion plasmas, which give rise to the micro-instabilities that cause turbulence, leading to the transport of heat and particles out of the confinement region of the device.
Recent studies have shown that the geometry of stellarator configurations can have a substantial impact on the stability properties of density-gradient-driven micro-instabilities (Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020). Maximum-${J}$![]() configurations like W7-XFootnote 1, where the value of the second adiabatic invariant ${J}$
configurations like W7-XFootnote 1, where the value of the second adiabatic invariant ${J}$![]() of trapped particle orbits decreases radially in the plasma, display beneficial attributes (Proll et al. Reference Proll, Helander, Connor and Plunk2012). First, it has been shown, both analytically and through numerical simulation by Helander, Proll & Plunk (Reference Helander, Proll and Plunk2013) and Proll, Xanthopoulos & Helander (Reference Proll, Xanthopoulos and Helander2013) that the trapped-electron mode (TEM), which is the dominant cause of density-gradient-driven turbulence in tokamaks, is stabilised by the maximum-${J}$
of trapped particle orbits decreases radially in the plasma, display beneficial attributes (Proll et al. Reference Proll, Helander, Connor and Plunk2012). First, it has been shown, both analytically and through numerical simulation by Helander, Proll & Plunk (Reference Helander, Proll and Plunk2013) and Proll, Xanthopoulos & Helander (Reference Proll, Xanthopoulos and Helander2013) that the trapped-electron mode (TEM), which is the dominant cause of density-gradient-driven turbulence in tokamaks, is stabilised by the maximum-${J}$![]() property, even if it is only satisfied locally for deeply trapped particles, as is the case in certain configurations of W7-X. In the absence of standard TEMs, the ion-driven trapped-electron mode (iTEM) has been shown to exist (Proll et al. Reference Proll, Xanthopoulos and Helander2013; Plunk, Connor & Helander Reference Plunk, Connor and Helander2017a). Finally, it has been anticipated by Helander & Plunk (Reference Helander and Plunk2015) that a further consequence of TEM stability in locally maximum-${J}$
property, even if it is only satisfied locally for deeply trapped particles, as is the case in certain configurations of W7-X. In the absence of standard TEMs, the ion-driven trapped-electron mode (iTEM) has been shown to exist (Proll et al. Reference Proll, Xanthopoulos and Helander2013; Plunk, Connor & Helander Reference Plunk, Connor and Helander2017a). Finally, it has been anticipated by Helander & Plunk (Reference Helander and Plunk2015) that a further consequence of TEM stability in locally maximum-${J}$![]() stellarators is the appearance of the universal instability. This instability mechanism differs from the TEM in that it is driven by wave–particle interactions involving passing electrons and does not rely on particle trapping to be unstable. Once thought to be common to all magnetic confinement devices, the universal instability is often overshadowed by TEMs in practice and, for a time, was thought to be completely stabilised in the presence of finite magnetic shear in slab geometry (Ross & Mahajan Reference Ross and Mahajan1978). However, recent gyrokinetic investigations have shown that it exists in sheared-slab geometry both linearly and nonlinearly (Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015a; Landreman, Plunk & Dorland Reference Landreman, Plunk and Dorland2015b), and a direct analogue of the slab instability mechanism may exist in toroidal geometry and may make a meaningful contribution to the growth of instabilities, provided that trapped-particle-driven modes are sufficiently weak (Helander & Plunk Reference Helander and Plunk2015). It has also been demonstrated that a toroidally driven universal mode exists, which relies on toroidal effects like curvature and gradients in magnetic field strength (Cheng & Chen Reference Cheng and Chen1980). This mode has been shown to be unstable in gyrokinetic simulations in tokamak geometry when examined in isolation, but becomes overshadowed by TEM drive when trapped particles are introduced (Chowdhury et al. Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010). The universal instability is yet to be observed in numerical simulations in stellarators, but it is speculated by Helander & Plunk (Reference Helander and Plunk2015) that it may appear in stellarator configurations which locally satisfy the maximum-$J$
stellarators is the appearance of the universal instability. This instability mechanism differs from the TEM in that it is driven by wave–particle interactions involving passing electrons and does not rely on particle trapping to be unstable. Once thought to be common to all magnetic confinement devices, the universal instability is often overshadowed by TEMs in practice and, for a time, was thought to be completely stabilised in the presence of finite magnetic shear in slab geometry (Ross & Mahajan Reference Ross and Mahajan1978). However, recent gyrokinetic investigations have shown that it exists in sheared-slab geometry both linearly and nonlinearly (Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015a; Landreman, Plunk & Dorland Reference Landreman, Plunk and Dorland2015b), and a direct analogue of the slab instability mechanism may exist in toroidal geometry and may make a meaningful contribution to the growth of instabilities, provided that trapped-particle-driven modes are sufficiently weak (Helander & Plunk Reference Helander and Plunk2015). It has also been demonstrated that a toroidally driven universal mode exists, which relies on toroidal effects like curvature and gradients in magnetic field strength (Cheng & Chen Reference Cheng and Chen1980). This mode has been shown to be unstable in gyrokinetic simulations in tokamak geometry when examined in isolation, but becomes overshadowed by TEM drive when trapped particles are introduced (Chowdhury et al. Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010). The universal instability is yet to be observed in numerical simulations in stellarators, but it is speculated by Helander & Plunk (Reference Helander and Plunk2015) that it may appear in stellarator configurations which locally satisfy the maximum-$J$![]() property due to the enhanced TEM stability.
property due to the enhanced TEM stability.
Here, we investigate the universal instability in density-gradient-driven turbulence in stellarators using gyrokinetic simulations. Linear simulations are used to examine the types of instabilities that exist in a variety of stellarator geometries, with a particular focus on W7-X. Nonlinear simulations are used to identify which of the linear instabilities are most representative of the features of saturated, density-gradient-driven turbulence.
1.1. Stellarator configurations considered
The stellarator configurations selected for this investigation are the high-mirror configuration of W7-X, the negative-mirror configuration of W7-X and the Helically Symmetric eXperiment (HSX) (Anderson et al. Reference Anderson, Almagri, Anderson, Matthews, Talmadge and Shohet1995). The high-mirror configuration of W7-X has been chosen as the focus of this investigation because it is an approximately quasi-isodynamic and locally maximum-$J$![]() configuration. The stability properties of TEMs and iTEMs in linear simulations of the high-mirror configuration of W7-X have been well documented in previous studies (Proll et al. Reference Proll, Xanthopoulos and Helander2013; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020). The negative-mirror configuration of W7-X is distinctly non-maximum-$J$
configuration. The stability properties of TEMs and iTEMs in linear simulations of the high-mirror configuration of W7-X have been well documented in previous studies (Proll et al. Reference Proll, Xanthopoulos and Helander2013; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020). The negative-mirror configuration of W7-X is distinctly non-maximum-$J$![]() in the regions of worst curvature for deeply trapped particles, providing an opportunity to observe how moving far from a maximum-$J$
in the regions of worst curvature for deeply trapped particles, providing an opportunity to observe how moving far from a maximum-$J$![]() configuration affects linear instabilities. HSX is selected as it achieves its lower neoclassical transport by different means than W7-X's quasi-isodynamicity, namely through quasi-helical symmetry, in which the magnetic field strength exhibits a helical symmetry in the toroidal and poloidal Boozer angles on each flux surface (Boozer Reference Boozer1995). This, however, grants none of the properties beneficial to TEM stability possessed by locally maximum-$J$
configuration affects linear instabilities. HSX is selected as it achieves its lower neoclassical transport by different means than W7-X's quasi-isodynamicity, namely through quasi-helical symmetry, in which the magnetic field strength exhibits a helical symmetry in the toroidal and poloidal Boozer angles on each flux surface (Boozer Reference Boozer1995). This, however, grants none of the properties beneficial to TEM stability possessed by locally maximum-$J$![]() configurations. Interestingly, it has been found that HSX performs well in nonlinear simulations of turbulent transport, despite the less favourable stability properties (McKinney et al. Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019; Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022).
configurations. Interestingly, it has been found that HSX performs well in nonlinear simulations of turbulent transport, despite the less favourable stability properties (McKinney et al. Reference McKinney, Pueschel, Faber, Hegna, Talmadge, Anderson, Mynick and Xanthopoulos2019; Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022).
Because the magnetic shear $\hat {s}= -r \iota '(r)/\iota (r)$![]() , where $r$
, where $r$![]() is the minor radial coordinate and $\iota$
is the minor radial coordinate and $\iota$![]() is the rotational transform, influences the stability of universal modes, it is noteworthy that all geometries considered in this study are low-shear configurations with $\hat {s}_{\text {HM}} = -0.1286351$
is the rotational transform, influences the stability of universal modes, it is noteworthy that all geometries considered in this study are low-shear configurations with $\hat {s}_{\text {HM}} = -0.1286351$![]() in W7-X high-mirror configuration, $\hat {s}_\text {{NM}} = -0.1406220$
in W7-X high-mirror configuration, $\hat {s}_\text {{NM}} = -0.1406220$![]() in W7-X negative-mirror configuration and $\hat {s}_\text {{HSX}} = -0.0449432$
in W7-X negative-mirror configuration and $\hat {s}_\text {{HSX}} = -0.0449432$![]() in HSX. All our simulations here, performed at a normalised density gradient value of $a/L_n = 3$
in HSX. All our simulations here, performed at a normalised density gradient value of $a/L_n = 3$![]() , where $a$
, where $a$![]() is the minor radius of the device, are above the slab-mode instability limit of $L_s/L_n \approx 17$
is the minor radius of the device, are above the slab-mode instability limit of $L_s/L_n \approx 17$![]() established by Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) and Helander & Plunk (Reference Helander and Plunk2015), where $L_s$
established by Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) and Helander & Plunk (Reference Helander and Plunk2015), where $L_s$![]() is the shear scale length given by $L_s = R/(\iota \hat {s})$
is the shear scale length given by $L_s = R/(\iota \hat {s})$![]() , where $R$
, where $R$![]() is the major radius and $L_n= d \ln (n)/dr$
is the major radius and $L_n= d \ln (n)/dr$![]() is the density gradient scale length. Specifically at $a/L_n = 3$
is the density gradient scale length. Specifically at $a/L_n = 3$![]() , we have $(L_s/L_n)_{\text {HM},3} \approx 270$
, we have $(L_s/L_n)_{\text {HM},3} \approx 270$![]() in the high-mirror configuration of W7-X , $(L_s/L_n)_{\text {NM},3} \approx 260$
in the high-mirror configuration of W7-X , $(L_s/L_n)_{\text {NM},3} \approx 260$![]() in the negative mirror configuration and $(L_s/L_n)_{\text {HSX},3} \approx 610$
in the negative mirror configuration and $(L_s/L_n)_{\text {HSX},3} \approx 610$![]() in HSX. Thus, it is possible that instabilities analogous to the universal slab modes may be observed in these configurations.
in HSX. Thus, it is possible that instabilities analogous to the universal slab modes may be observed in these configurations.
2. Theory
We will now briefly describe the theoretical background of the micro-instabilities of interest, namely the universal instability and the trapped-electron mode, in toroidal geometry. Here, we recount some of the key points of the theory of universal modes in general geometry shown by Helander & Plunk (Reference Helander and Plunk2015). In their work, both electrons and ions are treated kinetically. The distribution function of each species $a$![]() is assumed to be of the form $f_a = f_{a0}(1 + e_a \phi /T_a) + g_a$
is assumed to be of the form $f_a = f_{a0}(1 + e_a \phi /T_a) + g_a$![]() , where $f_{a0}$
, where $f_{a0}$![]() is a Maxwellian background distribution, $e_a \phi /T_a$
is a Maxwellian background distribution, $e_a \phi /T_a$![]() is the adiabatic response to the potential $\phi$
is the adiabatic response to the potential $\phi$![]() for a species $a$
for a species $a$![]() with charge $e_a$
with charge $e_a$![]() and temperature $T_a$
and temperature $T_a$![]() , and $g_a$
, and $g_a$![]() is a non-adiabatic perturbation of the distribution. In the electrostatic collisionless case, $g_a$
is a non-adiabatic perturbation of the distribution. In the electrostatic collisionless case, $g_a$![]() is governed by the gyrokinetic equation,
is governed by the gyrokinetic equation,
where the argument of the Bessel function is $J_0(k_\perp v_\perp /\varOmega _a)$![]() with the gyrofrequency $\varOmega _a = e_a B/m_a$
with the gyrofrequency $\varOmega _a = e_a B/m_a$![]() with $B = |\boldsymbol {B}|$
with $B = |\boldsymbol {B}|$![]() and $m_a$
and $m_a$![]() being the mass of species $a$
being the mass of species $a$![]() . The drift frequency is given by $\omega _{da} = \boldsymbol {v}_{da}\boldsymbol {\cdot } \boldsymbol {k}_{\perp }$
. The drift frequency is given by $\omega _{da} = \boldsymbol {v}_{da}\boldsymbol {\cdot } \boldsymbol {k}_{\perp }$![]() with the drift velocity of a particle in a magnetic field $\boldsymbol {v}_{da}$
with the drift velocity of a particle in a magnetic field $\boldsymbol {v}_{da}$![]() and the energy-dependent diamagnetic frequency,
and the energy-dependent diamagnetic frequency,
where $\omega _{*a}$![]() is the diamagnetic frequency, $\omega _{*a} = ({T_a}/{n_a e_a B^2})(\boldsymbol {k}_{\perp } \times \boldsymbol {B})\boldsymbol {\cdot } \boldsymbol {\nabla } n_a$
is the diamagnetic frequency, $\omega _{*a} = ({T_a}/{n_a e_a B^2})(\boldsymbol {k}_{\perp } \times \boldsymbol {B})\boldsymbol {\cdot } \boldsymbol {\nabla } n_a$![]() , while $\eta _a={{\rm d} \ln T_a}/{{\rm d} \ln n_a}$
, while $\eta _a={{\rm d} \ln T_a}/{{\rm d} \ln n_a}$![]() is the ratio between the normalised temperature and density gradients of each species, and $x^2 = m_a v^2/(2T_a)$
is the ratio between the normalised temperature and density gradients of each species, and $x^2 = m_a v^2/(2T_a)$![]() .
.
To describe an arbitrary stellarator configuration, we use the Clebsch representation of the magnetic field $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$![]() , where $\psi$
, where $\psi$![]() is the toroidal magnetic flux, and the Clebsch angle $\alpha = \theta - \iota \varphi$
is the toroidal magnetic flux, and the Clebsch angle $\alpha = \theta - \iota \varphi$![]() is constructed from the poloidal and toroidal angles $\theta$
is constructed from the poloidal and toroidal angles $\theta$![]() and $\varphi$
and $\varphi$![]() , respectively, and the rotational transform $\iota$
, respectively, and the rotational transform $\iota$![]() . This gives a perpendicular wavenumber of the form $\boldsymbol {k}_\perp = k_\psi \boldsymbol {\nabla } \psi + k_\alpha \boldsymbol {\nabla } \alpha$
. This gives a perpendicular wavenumber of the form $\boldsymbol {k}_\perp = k_\psi \boldsymbol {\nabla } \psi + k_\alpha \boldsymbol {\nabla } \alpha$![]() . The drift velocity of a particle in a non-homogeneous field is given by
. The drift velocity of a particle in a non-homogeneous field is given by
where $\boldsymbol {b} = \boldsymbol {B}/B$![]() and $\boldsymbol {\kappa } = \boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {b}$
and $\boldsymbol {\kappa } = \boldsymbol {b}\boldsymbol {\cdot } \boldsymbol {\nabla } \boldsymbol {b}$![]() , the curvature of the magnetic field lines.
, the curvature of the magnetic field lines.
This system of equations is then closed by the quasi-neutrality condition

where $n_a$![]() is the species density (from here, we assume $n_e = n_a \equiv n$
is the species density (from here, we assume $n_e = n_a \equiv n$![]() ). Considering the non-adiabatic ion distribution $g_i$
). Considering the non-adiabatic ion distribution $g_i$![]() in the limit of slow parallel ion motion ($i v_{\parallel } \nabla _{\parallel }g_i \approx 0$
in the limit of slow parallel ion motion ($i v_{\parallel } \nabla _{\parallel }g_i \approx 0$![]() ), and neglecting the ion drift frequency $\omega _{di}$
), and neglecting the ion drift frequency $\omega _{di}$![]() , the gyrokinetic equation, (2.1), gives
, the gyrokinetic equation, (2.1), gives
Inserting this into (2.4) yields
Here, the $\varGamma _n$![]() functions are modified Bessel functions $\varGamma _n = I_n(\textit {b}) e^{-b}$
functions are modified Bessel functions $\varGamma _n = I_n(\textit {b}) e^{-b}$![]() with the argument $b = k_{\perp }^2 \rho _i^2$
with the argument $b = k_{\perp }^2 \rho _i^2$![]() , where $\rho _i$
, where $\rho _i$![]() is the ion Larmor radius. Multiplying (2.6) by $\phi ^*$
is the ion Larmor radius. Multiplying (2.6) by $\phi ^*$![]() and integrating along a field line via $\int \text {d}l/B$
and integrating along a field line via $\int \text {d}l/B$![]() , where in ballooning space the field line extends infinitely in $l$
, where in ballooning space the field line extends infinitely in $l$![]() , gives
, gives
Expanding the frequency $\omega = \omega _r + i \gamma$![]() , the imaginary component of $1/\omega$
, the imaginary component of $1/\omega$![]() becomes $-\gamma /(\omega _r^2 + \gamma ^2)$
becomes $-\gamma /(\omega _r^2 + \gamma ^2)$![]() allowing us to separate the imaginary part of (2.8), giving
allowing us to separate the imaginary part of (2.8), giving
with
The sign of $\gamma$![]() is thus determined by $Q_e(\omega )$
is thus determined by $Q_e(\omega )$![]() with instability ($\gamma > 0$
with instability ($\gamma > 0$![]() ) occurring when $Q_e(\omega )/\omega _{*e} > 0$
) occurring when $Q_e(\omega )/\omega _{*e} > 0$![]() . The integral in velocity space of $g_e$
. The integral in velocity space of $g_e$![]() can be decomposed into separate integrals over the particles in the trapped region of velocity space and the passing region. This allows the contribution of trapped (index $t$
can be decomposed into separate integrals over the particles in the trapped region of velocity space and the passing region. This allows the contribution of trapped (index $t$![]() ) particles and passing (index $p$
) particles and passing (index $p$![]() ) particles to the growth rate $\gamma$
) particles to the growth rate $\gamma$![]() to be isolated by writing
to be isolated by writing
The procedure for this separation is outlined by Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Connor, Hastie & Taylor (Reference Connor, Hastie and Taylor1980). For brevity, we do not fully reproduce the expressions for $Q_{\rm ep}(\omega )$![]() and $Q_{\rm et}(\omega )$
and $Q_{\rm et}(\omega )$![]() but quote the result from Helander & Plunk (Reference Helander and Plunk2015). The passing-particle contribution to the energy transfer is
but quote the result from Helander & Plunk (Reference Helander and Plunk2015). The passing-particle contribution to the energy transfer is
where $\lambda = v_\perp ^2/(v^2B)$![]() ,
,
and
We see that, in the absence of a temperature gradient ($\eta _e = 0$![]() ), any mode with a real frequency $\omega /\omega _{*e} <1$
), any mode with a real frequency $\omega /\omega _{*e} <1$![]() may be driven unstable by the passing electrons. In most situations, $Q_{\rm et}(\omega )$
may be driven unstable by the passing electrons. In most situations, $Q_{\rm et}(\omega )$![]() ((10) in Helander & Plunk Reference Helander and Plunk2015) is much larger than $Q_{\rm ep}(\omega )$
((10) in Helander & Plunk Reference Helander and Plunk2015) is much larger than $Q_{\rm ep}(\omega )$![]() , thus dominating in contribution to $\gamma$
, thus dominating in contribution to $\gamma$![]() , resulting in a classical TEM, which is why passing-particle-driven universal instability modes of this nature are seldom observed. However, stellarator optimisation for the maximum-$J$
, resulting in a classical TEM, which is why passing-particle-driven universal instability modes of this nature are seldom observed. However, stellarator optimisation for the maximum-$J$![]() property has led to substantial reduction in TEM drive in geometries like W7-X, with the potential to further reduce TEM drive through schemes using proxies for TEM instability (Proll et al. Reference Proll, Mynick, Xanthopoulos, Lazerson and Faber2015; Gerard et al. Reference Gerard, Geiger, Pueschel, Bader, Hegna, Faber, Terry, Kumar and Schmitt2023).
property has led to substantial reduction in TEM drive in geometries like W7-X, with the potential to further reduce TEM drive through schemes using proxies for TEM instability (Proll et al. Reference Proll, Mynick, Xanthopoulos, Lazerson and Faber2015; Gerard et al. Reference Gerard, Geiger, Pueschel, Bader, Hegna, Faber, Terry, Kumar and Schmitt2023).
In these TEM stable geometries, it is possible that $Q_{\rm ep}(\omega )$![]() may become a relevant source of instability. Note that here, because we have neglected the role of the ion drift frequency $\omega _{di}$
may become a relevant source of instability. Note that here, because we have neglected the role of the ion drift frequency $\omega _{di}$![]() , the iTEM is absent from this analysis, but in fact, it has been observed that in devices which locally satisfy the maximum-$J$
, the iTEM is absent from this analysis, but in fact, it has been observed that in devices which locally satisfy the maximum-$J$![]() property, and thus have beneficial TEM stability properties, it is the iTEM which typically takes the place of the TEM in gyrokinetic simulations (Proll et al. Reference Proll, Xanthopoulos and Helander2013). By neglecting $\omega _{di}$
property, and thus have beneficial TEM stability properties, it is the iTEM which typically takes the place of the TEM in gyrokinetic simulations (Proll et al. Reference Proll, Xanthopoulos and Helander2013). By neglecting $\omega _{di}$![]() , we also remove the mechanism required for the toroidal universal instability of Cheng & Chen (Reference Cheng and Chen1980). We will later demonstrate, using numerical experiments in which we artificially remove $\omega _{de}$
, we also remove the mechanism required for the toroidal universal instability of Cheng & Chen (Reference Cheng and Chen1980). We will later demonstrate, using numerical experiments in which we artificially remove $\omega _{de}$![]() and $\omega _{di}$
and $\omega _{di}$![]() from our simulations, that the role of toroidal drifts is negligible, ruling out the toroidal universal instability as a candidate for the passing-electron-driven modes observed in our simulations.
from our simulations, that the role of toroidal drifts is negligible, ruling out the toroidal universal instability as a candidate for the passing-electron-driven modes observed in our simulations.
3. Gyrokinetic simulations and diagnostics
The numerical simulations in this study were performed with Gene (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000, see genecode.org for information). Gene is a continuum code that solves the linear or nonlinear gyrokinetic Vlasov–Maxwell system self-consistently. The numerical simulations in this study were carried out in flux-tube geometry, computed from the VMEC equilibrium of each stellarator by the geometry interface tool GIST (Xanthopoulos et al. Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). The flux-tube domain is discretised in the parallel coordinate $z$![]() , and Fourier transforms are taken in the radial $x$
, and Fourier transforms are taken in the radial $x$![]() direction and the binormal $y$
direction and the binormal $y$![]() direction, which correspond to the $\psi$
direction, which correspond to the $\psi$![]() and $\alpha$
and $\alpha$![]() coordinates from the Clebsch representation, respectively. Linear simulations were carried out as scans over the normalised binormal wavenumber $k_y \rho _s$
coordinates from the Clebsch representation, respectively. Linear simulations were carried out as scans over the normalised binormal wavenumber $k_y \rho _s$![]() , where $\rho _s = \sqrt {(T_e/m_i)}/\varOmega _i$
, where $\rho _s = \sqrt {(T_e/m_i)}/\varOmega _i$![]() is the ion sound gyroradius, for a fixed density gradient at zero temperature gradient. The resolution parameters for each linear simulation at each $k_y$
is the ion sound gyroradius, for a fixed density gradient at zero temperature gradient. The resolution parameters for each linear simulation at each $k_y$![]() in the high-mirror configuration of W7-X are $N_{kx} \times N_z \times N_{v_\parallel } \times N_\mu = 63 \times 96 \times 48 \times 12$
in the high-mirror configuration of W7-X are $N_{kx} \times N_z \times N_{v_\parallel } \times N_\mu = 63 \times 96 \times 48 \times 12$![]() , where $N_{kx}$
, where $N_{kx}$![]() is the number of radial Fourier modes, $N_z$
is the number of radial Fourier modes, $N_z$![]() is the number of points in $z$
is the number of points in $z$![]() , and $N_{v_\parallel }$
, and $N_{v_\parallel }$![]() and $N_\mu$
and $N_\mu$![]() are the number of grid points in velocity space in the parallel velocity $v_\parallel$
are the number of grid points in velocity space in the parallel velocity $v_\parallel$![]() and magnetic moment $\mu$
and magnetic moment $\mu$![]() , respectively. In the negative-mirror configuration, $N_z = 128$
, respectively. In the negative-mirror configuration, $N_z = 128$![]() was used, with the other values remaining the same, and in HSX, it has been shown that four poloidal turns are required to capture certain damping effects (Faber et al. Reference Faber, Pueschel, Terry, Hegna and Roman2018), so a corresponding extended flux tube with $N_z = 512$
was used, with the other values remaining the same, and in HSX, it has been shown that four poloidal turns are required to capture certain damping effects (Faber et al. Reference Faber, Pueschel, Terry, Hegna and Roman2018), so a corresponding extended flux tube with $N_z = 512$![]() was used. The criterion for numerical convergence used here is that eigenvalues change by less than 10 % upon doubling of any given resolution. The simulations were carried out with a realistic hydrogen mass ratio ${m_e}/{m_i} = 0.00054$
was used. The criterion for numerical convergence used here is that eigenvalues change by less than 10 % upon doubling of any given resolution. The simulations were carried out with a realistic hydrogen mass ratio ${m_e}/{m_i} = 0.00054$![]() with kinetically treated electrons and ions. All simulations were carried out in the electrostatic, vacuum-magnetic-field limit with $\beta = 0$
with kinetically treated electrons and ions. All simulations were carried out in the electrostatic, vacuum-magnetic-field limit with $\beta = 0$![]() .
.
In all stellarator geometries considered in this study, the so-called bean flux tube, with $\alpha = 0$![]() , was selected as the simulation domain. This flux-tube crosses through the bean-shaped cross-section of each device at the outboard midplane, and has previously been found to be the most unstable flux-tube for iTEMs in W7-X (Proll et al. Reference Proll, Xanthopoulos and Helander2013) and TEMs in HSX (Faber et al. Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015). Each flux tube selected is located at the radial position denoted in normalised flux coordinates as ${\psi }/{\psi _0} = 0.5$
, was selected as the simulation domain. This flux-tube crosses through the bean-shaped cross-section of each device at the outboard midplane, and has previously been found to be the most unstable flux-tube for iTEMs in W7-X (Proll et al. Reference Proll, Xanthopoulos and Helander2013) and TEMs in HSX (Faber et al. Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015). Each flux tube selected is located at the radial position denoted in normalised flux coordinates as ${\psi }/{\psi _0} = 0.5$![]() , which corresponds to ${r}/{a} \approx 0.71$
, which corresponds to ${r}/{a} \approx 0.71$![]() in terms of the minor radius $a$
in terms of the minor radius $a$![]() of each device. The boundary conditions for the flux-tube domain are the standard twist-and-shift described by Beer, Cowley & Hammett (Reference Beer, Cowley and Hammett1995).
of each device. The boundary conditions for the flux-tube domain are the standard twist-and-shift described by Beer, Cowley & Hammett (Reference Beer, Cowley and Hammett1995).
In the analysis of the linear simulations, the electrostatic energy transfer diagnostic (Bañón Navarro et al. Reference Bañón Navarro, Morel, Albrecht-Marc, Carati, Merz, Görler and Jenko2011) and the trapped-passing diagnostic were used. The energy transfer diagnostic allows for the computation of the rate of energy transfer between each species and the electrostatic potential of the instability $\phi$![]() . The trapped-passing diagnostic allows for analysis of the interaction between particles, which have trapped orbits in the magnetic geometry or are freely passing, and $\phi$
. The trapped-passing diagnostic allows for analysis of the interaction between particles, which have trapped orbits in the magnetic geometry or are freely passing, and $\phi$![]() . (Because the specification of a trapped-passing boundary in velocity space is non-trivial in a stellarator, here we use only a single trapping level, with the knowledge that this will not perfectly separate both populations, but should be sufficient to distinguish the unique signature of each mode.) To further analyse the underlying mechanisms of linear modes, we also conduct experiments by manually editing the GIST files and noting the impact this has on the observed modes. Notably, the resulting flux tubes are not self-consistent. In this manner, we construct configurations with a constant magnetic field strength in the parallel direction $B = B_{\text {ref}}$
. (Because the specification of a trapped-passing boundary in velocity space is non-trivial in a stellarator, here we use only a single trapping level, with the knowledge that this will not perfectly separate both populations, but should be sufficient to distinguish the unique signature of each mode.) To further analyse the underlying mechanisms of linear modes, we also conduct experiments by manually editing the GIST files and noting the impact this has on the observed modes. Notably, the resulting flux tubes are not self-consistent. In this manner, we construct configurations with a constant magnetic field strength in the parallel direction $B = B_{\text {ref}}$![]() , such that $\partial B /\partial z = 0$
, such that $\partial B /\partial z = 0$![]() , which we refer to as ‘homogeneous-$B$
, which we refer to as ‘homogeneous-$B$![]() ’ geometry, and configurations with $\mathcal {K}_1 = \mathcal {K}_2 = 0$
’ geometry, and configurations with $\mathcal {K}_1 = \mathcal {K}_2 = 0$![]() and $B = B_{\text {ref}}$
and $B = B_{\text {ref}}$![]() , which we refer to as ‘slab-like’ geometry, where the $\mathcal {K}_{1,2}$
, which we refer to as ‘slab-like’ geometry, where the $\mathcal {K}_{1,2}$![]() are the normal and binormal curvature components in GIST, respectively (Xanthopoulos et al. Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). In the limit of zero $\beta$
are the normal and binormal curvature components in GIST, respectively (Xanthopoulos et al. Reference Xanthopoulos, Cooper, Jenko, Turkin, Runov and Geiger2009). In the limit of zero $\beta$![]() , these are given by $\mathcal {K}_1 = \boldsymbol {b}\times \boldsymbol {\kappa }\boldsymbol {\cdot } \boldsymbol {\nabla } x$
, these are given by $\mathcal {K}_1 = \boldsymbol {b}\times \boldsymbol {\kappa }\boldsymbol {\cdot } \boldsymbol {\nabla } x$![]() and $\mathcal {K}_2 = \boldsymbol {b}\times \boldsymbol {\kappa }\boldsymbol {\cdot } \boldsymbol {\nabla } y$
and $\mathcal {K}_2 = \boldsymbol {b}\times \boldsymbol {\kappa }\boldsymbol {\cdot } \boldsymbol {\nabla } y$![]() , where $\boldsymbol {\kappa }$
, where $\boldsymbol {\kappa }$![]() is the curvature vector and all quantities are normalised appropriately in GIST. These tests serve two main purposes: first, the homogeneous-$B$
is the curvature vector and all quantities are normalised appropriately in GIST. These tests serve two main purposes: first, the homogeneous-$B$![]() geometry is used to separate TEMs from universal modes, due to the fact that setting $\partial B /\partial z = 0$
geometry is used to separate TEMs from universal modes, due to the fact that setting $\partial B /\partial z = 0$![]() prevents any particle trapping and trapped particle instabilities, such that modes that persist must be passing-particle-driven modes; second, the slab-like geometry then establishes the reliance of the remaining passing-particle modes on the curvature of magnetic field lines, which determines if the remaining modes are more akin to the slab modes of Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) or the toroidal modes of Chowdhury et al. (Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010). We note that setting $\partial B/ \partial z = 0$
prevents any particle trapping and trapped particle instabilities, such that modes that persist must be passing-particle-driven modes; second, the slab-like geometry then establishes the reliance of the remaining passing-particle modes on the curvature of magnetic field lines, which determines if the remaining modes are more akin to the slab modes of Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) or the toroidal modes of Chowdhury et al. (Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010). We note that setting $\partial B/ \partial z = 0$![]() in GIST has an impact on the curvature operators implemented in Gene, but this is not of consequence for our purposes of differentiating universal modes from TEMs.
in GIST has an impact on the curvature operators implemented in Gene, but this is not of consequence for our purposes of differentiating universal modes from TEMs.
4. The universal instability in stellarators
Linear simulations were performed in each geometry at a normalised density gradient value of $a/L_n = 3$![]() , in the absence of any temperature gradient ($a/L_{Ti} = 0$
, in the absence of any temperature gradient ($a/L_{Ti} = 0$![]() , $a/L_{Te} = 0$
, $a/L_{Te} = 0$![]() ).
).
4.1. W7-X high-mirror configuration
Performing linear simulations in the high-mirror configuration of W7-X, for $k_y\rho _s \geq 0.5$![]() , trapped-particle modes are observed. This is indicated by the mode structure, which peaks only in the regions of alignment of bad curvature (indicated by regions of $\mathcal {K}_2 <0$
, trapped-particle modes are observed. This is indicated by the mode structure, which peaks only in the regions of alignment of bad curvature (indicated by regions of $\mathcal {K}_2 <0$![]() , where the electron diamagnetic drift and the binormal curvature drift are in the same direction) and minima in magnetic field strength $B(z)$
, where the electron diamagnetic drift and the binormal curvature drift are in the same direction) and minima in magnetic field strength $B(z)$![]() (see figure 1), and by the linear cross-phases shown in figure 2(b), which display a large phase-shift between the trapped-electron population density $n_{\rm trap}$
(see figure 1), and by the linear cross-phases shown in figure 2(b), which display a large phase-shift between the trapped-electron population density $n_{\rm trap}$![]() and the electrostatic potential $\phi$
and the electrostatic potential $\phi$![]() for $k_y\rho _s \geq 0.5$
for $k_y\rho _s \geq 0.5$![]() . From the real frequencies $\omega$
. From the real frequencies $\omega$![]() shown in figure 2(a), the majority of modes in this region have been identified as iTEMs, with $\omega >0$
shown in figure 2(a), the majority of modes in this region have been identified as iTEMs, with $\omega >0$![]() indicating drift in the ion-diamagnetic direction. This is supported by the energy diagnostic, which confirms that the real frequency $\omega$
indicating drift in the ion-diamagnetic direction. This is supported by the energy diagnostic, which confirms that the real frequency $\omega$![]() of the mode is positive where ions are the primary driving species and negative where electrons dominate the mode drive. The two lowest $k_y\rho _s$
of the mode is positive where ions are the primary driving species and negative where electrons dominate the mode drive. The two lowest $k_y\rho _s$![]() modes simulated are classical electron-driven TEMs. The linear growth rate $\gamma$
modes simulated are classical electron-driven TEMs. The linear growth rate $\gamma$![]() peaks in the iTEM range at $k_y\rho _s = 1.3$
peaks in the iTEM range at $k_y\rho _s = 1.3$![]() .
.

Figure 1. Parallel structure of electrostatic potential $|\phi |$![]() linear eigenmodes in the high-mirror configuration of W7-X. Shown is a mode from the iTEM branch ($k_y \rho _s = 1$
linear eigenmodes in the high-mirror configuration of W7-X. Shown is a mode from the iTEM branch ($k_y \rho _s = 1$![]() ) and the $k_y\rho _s=0.3$
) and the $k_y\rho _s=0.3$![]() mode with broad mode structure alongside the magnetic field strength $B(z)$
mode with broad mode structure alongside the magnetic field strength $B(z)$![]() (blue dot–dashed line) and $\mathcal {K}_2$
(blue dot–dashed line) and $\mathcal {K}_2$![]() (black dashed line). The iTEM has the expected feature of peaking in the regions where the minima in $B(z)$
(black dashed line). The iTEM has the expected feature of peaking in the regions where the minima in $B(z)$![]() and $\mathcal {K}_2 <0$
and $\mathcal {K}_2 <0$![]() overlap.
overlap.

Figure 2. Results from linear simulations in W7-X high-mirror configuration. (a) Real frequencies $\omega$![]() and growth rates $\gamma$
and growth rates $\gamma$![]() at each $k_y$
at each $k_y$![]() are shown, and (b) cross-phase $\alpha$
are shown, and (b) cross-phase $\alpha$![]() between the electrostatic potential $\phi$
between the electrostatic potential $\phi$![]() and the trapped and passing electron density perturbations, respectively, are shown. Modes in the range $0.15 \leq k_y\rho _s \leq 0.4$
and the trapped and passing electron density perturbations, respectively, are shown. Modes in the range $0.15 \leq k_y\rho _s \leq 0.4$![]() lie on a distinct frequency branch in the electron diamagnetic direction ($\omega <0$
lie on a distinct frequency branch in the electron diamagnetic direction ($\omega <0$![]() ), and exhibit a unique signature in $\alpha$
), and exhibit a unique signature in $\alpha$![]() .
.
In the range $0.15 \leq k_y\rho _s \leq 0.4$![]() , a substantially different type of mode is found, which is driven by electrons and stabilised by ions. These low-$k_y$
, a substantially different type of mode is found, which is driven by electrons and stabilised by ions. These low-$k_y$![]() modes are characterised by a broad, centrally peaked parallel mode structure. Comparing modes of this type to trapped-particle modes in the high-mirror configuration in figure 1, we see the modes differ, with the low-$k_y$
modes are characterised by a broad, centrally peaked parallel mode structure. Comparing modes of this type to trapped-particle modes in the high-mirror configuration in figure 1, we see the modes differ, with the low-$k_y$![]() modes exhibiting a peak in the $\mathcal {K}_2 < 0$
modes exhibiting a peak in the $\mathcal {K}_2 < 0$![]() region at $z=0$
region at $z=0$![]() , despite the maximum in $B(z)$
, despite the maximum in $B(z)$![]() . This is in contrast to the anticipated minima in the trapped-particle mode amplitude.
. This is in contrast to the anticipated minima in the trapped-particle mode amplitude.
By examining the mode frequency and growth rate in figure 2(a), we find that these modes again differ from trapped-particle modes. At these $k_y\rho _s$![]() values, $\omega$
values, $\omega$![]() lies on a distinct frequency branch with drift in the electron diamagnetic direction ($\omega < 0$
lies on a distinct frequency branch with drift in the electron diamagnetic direction ($\omega < 0$![]() ). These modes also exhibit a peak in growth rate at $k_y\rho _s = 0.3$
). These modes also exhibit a peak in growth rate at $k_y\rho _s = 0.3$![]() . Additionally, we find that these low-$k_y$
. Additionally, we find that these low-$k_y$![]() modes peak at a finite radial wavenumber $k_x\rho _s \neq 0$
modes peak at a finite radial wavenumber $k_x\rho _s \neq 0$![]() .
.
The linear cross-phases (see figure 2b) of these modes show further distinction from the TEM and iTEM. For these modes, the $n_{\rm trap}$![]() and (passing electron) $n_{\rm pass}$
and (passing electron) $n_{\rm pass}$![]() populations are both almost in phase with the potential, displaying only a small phase shift for both populations, with $n_{\rm pass}$
populations are both almost in phase with the potential, displaying only a small phase shift for both populations, with $n_{\rm pass}$![]() being slightly less in phase. We note that the passing electrons are in phase with the potential at the iTEM scales.
being slightly less in phase. We note that the passing electrons are in phase with the potential at the iTEM scales.
To classify the modes identified in the range $0.15 \leq k_y\rho _s \leq 0.4$![]() , we perform a numerical experiment. We repeat the simulations at the same parameters in W7-X high-mirror homogeneous-$B$
, we perform a numerical experiment. We repeat the simulations at the same parameters in W7-X high-mirror homogeneous-$B$![]() and slab-like geometries. In the homogeneous-$B$
and slab-like geometries. In the homogeneous-$B$![]() simulations, the modes identified in the unmodified high-mirror configuration in the range $0.15 \leq k_y\rho _s \leq 0.4$
simulations, the modes identified in the unmodified high-mirror configuration in the range $0.15 \leq k_y\rho _s \leq 0.4$![]() persist, despite the absence of any trapped-particle drive, allowing them to be identified as universal instabilities. In this modified geometry, the universal modes show little change in frequency or mode structure (see figures 3 and 4), with the mode structure, shown in figure 3, continuing to peak in the regions of $\mathcal {K}_2 < 0$
persist, despite the absence of any trapped-particle drive, allowing them to be identified as universal instabilities. In this modified geometry, the universal modes show little change in frequency or mode structure (see figures 3 and 4), with the mode structure, shown in figure 3, continuing to peak in the regions of $\mathcal {K}_2 < 0$![]() . In this modified configuration, these modes also exist over a wider range of $k_y\rho _s$
. In this modified configuration, these modes also exist over a wider range of $k_y\rho _s$![]() values $0.1 \leq k_y\rho _s \leq 1$
values $0.1 \leq k_y\rho _s \leq 1$![]() . The growth rates in this geometry align well with the unmodified high-mirror configuration growth rates at $k_y\rho _s \leq 0.3$
. The growth rates in this geometry align well with the unmodified high-mirror configuration growth rates at $k_y\rho _s \leq 0.3$![]() but begin to deviate at larger $k_y$
but begin to deviate at larger $k_y$![]() .
.

Figure 3. Comparison of linear $|\phi |$![]() eigenmodes in W7-X high-mirror configuration and in homogeneous-$B$
eigenmodes in W7-X high-mirror configuration and in homogeneous-$B$![]() and slab-like W7-X high-mirror geometry. A universal mode in W7-X high-mirror geometry at $k_y\rho _s = 0.3$
and slab-like W7-X high-mirror geometry. A universal mode in W7-X high-mirror geometry at $k_y\rho _s = 0.3$![]() is shown alongside a mode of the same $k_y$
is shown alongside a mode of the same $k_y$![]() in the modified geometries, with the unmodified high-mirror $B(z)$
in the modified geometries, with the unmodified high-mirror $B(z)$![]() (dot–dashed blue) and $\mathcal {K}_2$
(dot–dashed blue) and $\mathcal {K}_2$![]() (dashed black).
(dashed black).

Figure 4. Comparison of results of linear simulations in W7-X high-mirror configuration and in homogeneous-$B$![]() and slab-like W7-X high-mirror geometry. (a) Real frequencies $\omega$
and slab-like W7-X high-mirror geometry. (a) Real frequencies $\omega$![]() in each geometry and (b) growth rates $\gamma$
in each geometry and (b) growth rates $\gamma$![]() . In panel (a), the low-$k_y$
. In panel (a), the low-$k_y$![]() universal mode frequency branch can be seen to persist despite the removal of trapped electrons and curvature, and in panel (b), the growth rates of these modes are found to increase, likely due to the removal of non-resonant trapped electrons from the system.
universal mode frequency branch can be seen to persist despite the removal of trapped electrons and curvature, and in panel (b), the growth rates of these modes are found to increase, likely due to the removal of non-resonant trapped electrons from the system.
In the homogeneous-$B$![]() simulations, as $k_y$
simulations, as $k_y$![]() increases above $k_y\rho _s > 1$
increases above $k_y\rho _s > 1$![]() , the universal modes become strongly localised at $z =0$
, the universal modes become strongly localised at $z =0$![]() and seem to lie on a branch distinct from that of the broader-mode-structure universal modes found at $k_y\rho _s \leq 1$
and seem to lie on a branch distinct from that of the broader-mode-structure universal modes found at $k_y\rho _s \leq 1$![]() . We note that the removal of trapped electrons in W7-X increases the growth rate of universal modes in the range $0.3 \leq k_y\rho _s\leq 0.7$
. We note that the removal of trapped electrons in W7-X increases the growth rate of universal modes in the range $0.3 \leq k_y\rho _s\leq 0.7$![]() , which encapsulates some of the $k_y$
, which encapsulates some of the $k_y$![]() values at which these modes are observed in the unmodified geometry, suggesting that the trapped-electron population in a locally maximum-$J$
values at which these modes are observed in the unmodified geometry, suggesting that the trapped-electron population in a locally maximum-$J$![]() device has a stabilising effect on these modes.
device has a stabilising effect on these modes.
To determine the effect of magnetic curvature on these instabilities, we repeat the $B(z) = \text {const.}$![]() simulations in the modified slab-like W7-X high-mirror geometry (also shown in figures 3 and 4). We observe in figure 4 that the frequencies and growth rates of the universal modes which are found for $0.15 \leq k_y\rho _s \leq 0.4$
simulations in the modified slab-like W7-X high-mirror geometry (also shown in figures 3 and 4). We observe in figure 4 that the frequencies and growth rates of the universal modes which are found for $0.15 \leq k_y\rho _s \leq 0.4$![]() in the unmodified high-mirror geometry are largely unaffected by magnetic curvature. This rules out the toroidal universal instability of Cheng & Chen (Reference Cheng and Chen1980). The localisation of the mode structure $\phi$
in the unmodified high-mirror geometry are largely unaffected by magnetic curvature. This rules out the toroidal universal instability of Cheng & Chen (Reference Cheng and Chen1980). The localisation of the mode structure $\phi$![]() along the field line is changed slightly, but otherwise, the instability appears unchanged. If these modes were of similar nature to the toroidal modes of Chowdhury et al. (Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010), we would expect a large reduction in the growth rates of these modes with the removal of curvature. For the highly localised modes at $k_y\rho _s > 1$
along the field line is changed slightly, but otherwise, the instability appears unchanged. If these modes were of similar nature to the toroidal modes of Chowdhury et al. (Reference Chowdhury, Ganesh, Brunner, Vaclavik and Villard2010), we would expect a large reduction in the growth rates of these modes with the removal of curvature. For the highly localised modes at $k_y\rho _s > 1$![]() , the removal of the curvature terms $\mathcal {K}_1$
, the removal of the curvature terms $\mathcal {K}_1$![]() and $\mathcal {K}_2$
and $\mathcal {K}_2$![]() results in a more significant decrease in growth rate and real frequency, which could indicate that the $k_y\rho _s>1$
results in a more significant decrease in growth rate and real frequency, which could indicate that the $k_y\rho _s>1$![]() modes are more toroidal in nature.
modes are more toroidal in nature.
Thus, from these results, we can conclude that in the high-mirror configuration of W7-X, the reduction of the TEM drive $Q_{\rm et}$![]() , due to the maximum-$J$
, due to the maximum-$J$![]() nature of the most deeply trapped electrons in the region of worst curvature at $z=0$
nature of the most deeply trapped electrons in the region of worst curvature at $z=0$![]() , allows modes primarily driven by the passing electrons (as described by the term $Q_{\rm ep}$
, allows modes primarily driven by the passing electrons (as described by the term $Q_{\rm ep}$![]() in (2.12)) to become the fastest-growing instabilities over a range of $k_y$
in (2.12)) to become the fastest-growing instabilities over a range of $k_y$![]() . However, as evidenced by our numerical experiments, the stabilising nature of trapped electrons in W7-X also seems to reduce the overall growth rate of these universal modes.
. However, as evidenced by our numerical experiments, the stabilising nature of trapped electrons in W7-X also seems to reduce the overall growth rate of these universal modes.
Figure 5 shows results from Gene's eigenvalue solver, from which we find that unstable classical electron-driven TEMs exist at the same $k_y$![]() scales at which universal modes dominate. At $k_y\rho _s = 0.2$
scales at which universal modes dominate. At $k_y\rho _s = 0.2$![]() , (the mode shown in figure 5) the universal mode has a growth rate of $\gamma =0.086$
, (the mode shown in figure 5) the universal mode has a growth rate of $\gamma =0.086$![]() with a frequency of $\omega = -0.3853$
with a frequency of $\omega = -0.3853$![]() and the TEM growth rate is $\gamma = 0.051$
and the TEM growth rate is $\gamma = 0.051$![]() with $\omega = -0.0114$
with $\omega = -0.0114$![]() . Thus, TEMs have been sufficiently stabilised by the local maximum-$J$
. Thus, TEMs have been sufficiently stabilised by the local maximum-$J$![]() property, satisfied for the deeply trapped electrons in the region of worst curvature, so that they become subdominant to the universal modes in the high-mirror configuration of W7-X.
property, satisfied for the deeply trapped electrons in the region of worst curvature, so that they become subdominant to the universal modes in the high-mirror configuration of W7-X.

Figure 5. Parallel mode structures of $|\phi |$![]() from eigenvalue simulations indicate the presence of dominant universal modes and subdominant TEMs at the same scale, ($k_y\rho _s = 0.2)$
from eigenvalue simulations indicate the presence of dominant universal modes and subdominant TEMs at the same scale, ($k_y\rho _s = 0.2)$![]() , shown here alongside $B(z)$
, shown here alongside $B(z)$![]() (dot–dashed blue) and $\mathcal {K}_2$
(dot–dashed blue) and $\mathcal {K}_2$![]() (dashed black).
(dashed black).
4.2. W7-X negative-mirror configuration
The linear simulations in W7-X negative-mirror configuration show the large impact that the lack of quasi-isodynamicity and maximum-$J$![]() property have on trapped-particle instabilities. In figure 7, at the majority of $k_y\rho _s$
property have on trapped-particle instabilities. In figure 7, at the majority of $k_y\rho _s$![]() values, we observe classical electron-driven TEMs with $\omega <0$
values, we observe classical electron-driven TEMs with $\omega <0$![]() and much higher growth rates than the iTEMs which appear in the high-mirror configuration (see figure 7a). These TEMs also have the characteristic large cross-phase of $\alpha \approx {\rm \pi}/2$
and much higher growth rates than the iTEMs which appear in the high-mirror configuration (see figure 7a). These TEMs also have the characteristic large cross-phase of $\alpha \approx {\rm \pi}/2$![]() between the electron density $n_{\text {trap}}$
between the electron density $n_{\text {trap}}$![]() and $\phi$
and $\phi$![]() .
.
In contrast to the high-mirror configuration, due to the dominance of TEMs at most $k_y$![]() values, we observe only two modes that fit the description of the universal instability identified above. One such mode appears at $k_y\rho _s = 0.2$
values, we observe only two modes that fit the description of the universal instability identified above. One such mode appears at $k_y\rho _s = 0.2$![]() , where the mode structure is broad and centrally peaked, as in the high-mirror configuration. The other mode which may be of this type, at $k_y\rho _s = 0.3$
, where the mode structure is broad and centrally peaked, as in the high-mirror configuration. The other mode which may be of this type, at $k_y\rho _s = 0.3$![]() however, peaks at $z \approx {\rm \pi}/2$
however, peaks at $z \approx {\rm \pi}/2$![]() , like the TEMs which immediately follow. Thus, it is likely that this mode has substantial TEM drive and is more akin to a universal-TEM hybrid mode than a pure universal instability, similar to the TEM/ion-temperature-gradient (ITG) hybrid modes reported by Kammerer, Merz & Jenko (Reference Kammerer, Merz and Jenko2008). These modes are shown in figure 6, where, at $k_y\rho _s = 0.2$
, like the TEMs which immediately follow. Thus, it is likely that this mode has substantial TEM drive and is more akin to a universal-TEM hybrid mode than a pure universal instability, similar to the TEM/ion-temperature-gradient (ITG) hybrid modes reported by Kammerer, Merz & Jenko (Reference Kammerer, Merz and Jenko2008). These modes are shown in figure 6, where, at $k_y\rho _s = 0.2$![]() , the familiar universal instability mode structure is observed and the TEM dominates as $k_y$
, the familiar universal instability mode structure is observed and the TEM dominates as $k_y$![]() increases. Indeed, repeating these simulations in modified, homogeneous-$B$
increases. Indeed, repeating these simulations in modified, homogeneous-$B$![]() W7-X negative-mirror geometry, we find that only the dominant modes at $k_y\rho _s = 0.2$
W7-X negative-mirror geometry, we find that only the dominant modes at $k_y\rho _s = 0.2$![]() and $0.3$
and $0.3$![]() retain their frequency and growth rate, and that the universal-TEM hybrid mode is replaced by the centrally peaked universal mode structure.
retain their frequency and growth rate, and that the universal-TEM hybrid mode is replaced by the centrally peaked universal mode structure.

Figure 6. Parallel structures of three successive $k_y$![]() modes in W7-X negative-mirror configuration, a universal instability mode at $k_y\rho _s=0.2$
modes in W7-X negative-mirror configuration, a universal instability mode at $k_y\rho _s=0.2$![]() (magenta), a universal-TEM hybrid mode at $k_y\rho _s = 0.3$
(magenta), a universal-TEM hybrid mode at $k_y\rho _s = 0.3$![]() (red), and a TEM at $k_y \rho _s = 1$
(red), and a TEM at $k_y \rho _s = 1$![]() (orange) alongside $B(z)$
(orange) alongside $B(z)$![]() (dot–dashed blue) and $\mathcal {K}_2$
(dot–dashed blue) and $\mathcal {K}_2$![]() (dashed black).
(dashed black).
Interestingly, the cross-phases of $n_{\rm pass}$![]() in W7-X negative-mirror configuration show less in-phase behaviour at higher $k_y$
in W7-X negative-mirror configuration show less in-phase behaviour at higher $k_y$![]() than in the locally maximum-$J$
than in the locally maximum-$J$![]() high-mirror configuration, see figure 7(b). This may indicate that the classical TEMs, which, like the universal instability, have a frequency in the electron diamagnetic direction (see figure 7a), are also partly driven by $Q_{\rm ep}$
high-mirror configuration, see figure 7(b). This may indicate that the classical TEMs, which, like the universal instability, have a frequency in the electron diamagnetic direction (see figure 7a), are also partly driven by $Q_{\rm ep}$![]() . It is clear, however, that modes driven by $Q_{\rm et}$
. It is clear, however, that modes driven by $Q_{\rm et}$![]() are much more prevalent in the negative-mirror configuration of W7-X than the high-mirror configuration, overpowering the universal $Q_{\rm ep}$
are much more prevalent in the negative-mirror configuration of W7-X than the high-mirror configuration, overpowering the universal $Q_{\rm ep}$![]() -driven modes at most simulated scales.
-driven modes at most simulated scales.

Figure 7. Results from linear simulations in the negative-mirror configuration of W7-X. (a) Real frequency $\omega$![]() and growth rate $\gamma$
and growth rate $\gamma$![]() , and (b) cross-phases $\alpha$
, and (b) cross-phases $\alpha$![]() between the electrostatic potential $\phi$
between the electrostatic potential $\phi$![]() and the trapped and passing electron density perturbations. In panel (a), many more classical TEMs with $\omega <0$
and the trapped and passing electron density perturbations. In panel (a), many more classical TEMs with $\omega <0$![]() and larger $\gamma$
and larger $\gamma$![]() than the iTEMs seen in the high-mirror configuration are shown, and in panel (b), only two modes at $k_y\rho _s = 0.2$
than the iTEMs seen in the high-mirror configuration are shown, and in panel (b), only two modes at $k_y\rho _s = 0.2$![]() and $0.3$
and $0.3$![]() have the cross-phase signature of the low-$k_y$
have the cross-phase signature of the low-$k_y$![]() universal modes seen in the high-mirror configuration.
universal modes seen in the high-mirror configuration.
4.3. Quasi-helically symmetric configuration
In the quasi-helically symmetric HSX, the regions of bad curvature align exactly with the minima of $B(z)$![]() along the flux tube, meaning that a TEM, which exclusively peaks in such regions of overlap, and a universal instability mode, which seems to peak predominantly in regions of bad curvature, are difficult to distinguish based on mode structure alone. In linear simulations in HSX geometry, for $k_y\rho _s > 0.5$
along the flux tube, meaning that a TEM, which exclusively peaks in such regions of overlap, and a universal instability mode, which seems to peak predominantly in regions of bad curvature, are difficult to distinguish based on mode structure alone. In linear simulations in HSX geometry, for $k_y\rho _s > 0.5$![]() , we find classical TEMs alongside iTEMs, in agreement with Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015). ( Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015) refer to what we call the iTEM as the UTEM (ubiquitous TEM), which was later called the iTEM by Plunk et al. (Reference Plunk, Connor and Helander2017a) when the physical mechanism was described.) These simulations also reveal modes at $k_y\rho _s \leq 0.5$
, we find classical TEMs alongside iTEMs, in agreement with Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015). ( Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015) refer to what we call the iTEM as the UTEM (ubiquitous TEM), which was later called the iTEM by Plunk et al. (Reference Plunk, Connor and Helander2017a) when the physical mechanism was described.) These simulations also reveal modes at $k_y\rho _s \leq 0.5$![]() that fit our established definition of universal modes. These modes are once again found to peak in the regions of bad curvature. One such mode at $k_y\rho _s= 0.3$
that fit our established definition of universal modes. These modes are once again found to peak in the regions of bad curvature. One such mode at $k_y\rho _s= 0.3$![]() is shown in figure 8, alongside a trapped-particle mode. It is only possible to identify these modes as universal instabilities by the linear cross-phases in figure 9(b) and by repeating the simulations in homogeneous-$B$
is shown in figure 8, alongside a trapped-particle mode. It is only possible to identify these modes as universal instabilities by the linear cross-phases in figure 9(b) and by repeating the simulations in homogeneous-$B$![]() HSX geometry (as detailed in § 3). These modes persist despite the absence of trapped particles and retain their mode structure. This can be seen in figure 10, where the low-$k_y$
HSX geometry (as detailed in § 3). These modes persist despite the absence of trapped particles and retain their mode structure. This can be seen in figure 10, where the low-$k_y$![]() modes largely remain unchanged in their growth rates and frequencies. We note that the removal of trapped electrons from HSX in the homogeneous-$B$
modes largely remain unchanged in their growth rates and frequencies. We note that the removal of trapped electrons from HSX in the homogeneous-$B$![]() simulations does not lead to the increase in growth rate observed for some universal modes in figure 4, further indicating the stabilising effect of trapped electrons on these modes in locally maximum-$J$
simulations does not lead to the increase in growth rate observed for some universal modes in figure 4, further indicating the stabilising effect of trapped electrons on these modes in locally maximum-$J$![]() configurations like the high-mirror configuration of W7-X.
configurations like the high-mirror configuration of W7-X.

Figure 8. Parallel mode structure of the electrostatic potential $|\phi |$![]() in linear simulations in HSX. Shown is a universal mode which is extended in $z$
in linear simulations in HSX. Shown is a universal mode which is extended in $z$![]() at $k_y\rho _s = 0.3$
at $k_y\rho _s = 0.3$![]() , and a TEM which is localised at $z = 0$
, and a TEM which is localised at $z = 0$![]() at $k_y\rho _s = 1$
at $k_y\rho _s = 1$![]() , alongside $B(z)$
, alongside $B(z)$![]() (dot–dashed blue) and $\mathcal {K}_2$
(dot–dashed blue) and $\mathcal {K}_2$![]() (dashed black).
(dashed black).

Figure 9. Results of linear simulations in HSX. (a) Real frequency $\omega$![]() and growth rate $\gamma$
and growth rate $\gamma$![]() , and (b) cross-phases between the electrostatic potential $\phi$
, and (b) cross-phases between the electrostatic potential $\phi$![]() and the trapped and passing electron density perturbations. In panel (a), most modes propagate in the electron-diamagnetic direction ($\omega <0$
and the trapped and passing electron density perturbations. In panel (a), most modes propagate in the electron-diamagnetic direction ($\omega <0$![]() ) and in panel (b), at $k_y\rho _s \leq 0.5$
) and in panel (b), at $k_y\rho _s \leq 0.5$![]() , display a similar cross-phase signature to universal modes observed in W7-X.
, display a similar cross-phase signature to universal modes observed in W7-X.

Figure 10. Comparison between (a) frequencies $\omega$![]() and (b) growth rates $\gamma$
and (b) growth rates $\gamma$![]() of modes in HSX and modified homogeneous-$B$
of modes in HSX and modified homogeneous-$B$![]() HSX geometry. Modes with $k_y\rho _s \leq 0.5$
HSX geometry. Modes with $k_y\rho _s \leq 0.5$![]() exhibit little change in growth rate or frequency if the geometry is modified to remove trapped electrons.
exhibit little change in growth rate or frequency if the geometry is modified to remove trapped electrons.
In standard HSX geometry, universal modes transition to TEMs with little change in mode structure for $k_y\rho _s > 0.5$![]() ; the TEMs then become strongly localised at $z = 0$
; the TEMs then become strongly localised at $z = 0$![]() on the outboard midplane for $k_y\rho _s\geq 0.9$
on the outboard midplane for $k_y\rho _s\geq 0.9$![]() , as shown in figure 8. Once more, we find that the $k_y \leq 0.5$
, as shown in figure 8. Once more, we find that the $k_y \leq 0.5$![]() universal modes peak at $k_x \rho _s \neq 0$
universal modes peak at $k_x \rho _s \neq 0$![]() .
.
It is surprising to find the universal instability in a configuration with no beneficial TEM stability properties when very few dominant universal modes were found in the W7-X negative-mirror configuration, due to the prevalence of the TEM. Because the trapped electron population can contribute additional instability drive to any electron-driven mode via $Q_{\rm et}$![]() in (2.11), it may be the case that, in HSX geometry, due to the fact that the minima in $B(z)$
in (2.11), it may be the case that, in HSX geometry, due to the fact that the minima in $B(z)$![]() , where the trapped electrons reside, align directly with the regions of $\mathcal {K}_2<0$
, where the trapped electrons reside, align directly with the regions of $\mathcal {K}_2<0$![]() all along the field line, more trapped electrons have the possibility to be resonant with universal modes than in the negative-mirror configuration of W7-X, where not all of the trapping regions have net bad curvature. This may allow universal modes to be driven by both $Q_{\rm ep}$
all along the field line, more trapped electrons have the possibility to be resonant with universal modes than in the negative-mirror configuration of W7-X, where not all of the trapping regions have net bad curvature. This may allow universal modes to be driven by both $Q_{\rm ep}$![]() and $Q_{\rm et}$
and $Q_{\rm et}$![]() , giving rise to universal–TEM hybrid modes, which are driven by both trapped and passing electrons. This may make the distinction between universal modes and TEMs somewhat arbitrary in HSX, as both populations contribute to the growth of the mode. Nevertheless, it is important to note that $Q_{\rm ep}$
, giving rise to universal–TEM hybrid modes, which are driven by both trapped and passing electrons. This may make the distinction between universal modes and TEMs somewhat arbitrary in HSX, as both populations contribute to the growth of the mode. Nevertheless, it is important to note that $Q_{\rm ep}$![]() does appear to make a meaningful contribution to turbulence in this configuration, a fact that must be considered if TEM turbulence is to be reduced in HSX-like configurations in the future.
does appear to make a meaningful contribution to turbulence in this configuration, a fact that must be considered if TEM turbulence is to be reduced in HSX-like configurations in the future.
In contrast to the expectation from slab geometry, we have found universal modes to be unstable, and of consequence for $k_y\rho _s < 0.5$![]() in low-shear stellarator geometries. (Note: the $k_y\rho _i >0.7$
in low-shear stellarator geometries. (Note: the $k_y\rho _i >0.7$![]() limit of Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) translates to $k_y\rho _s >0.5$
limit of Landreman et al. (Reference Landreman, Antonsen and Dorland2015a) translates to $k_y\rho _s >0.5$![]() under our normalisation when the differing factor of $\sqrt {2}$
under our normalisation when the differing factor of $\sqrt {2}$![]() from $\rho _i = \sqrt {2T_i/m_i}$
from $\rho _i = \sqrt {2T_i/m_i}$![]() is taken into account.) This may be due to the non-secular variation in $k_\perp ^2 = k_y^2g^{yy} + 2k_xk_y g^{xy} + k_x^2 g^{xx}$
is taken into account.) This may be due to the non-secular variation in $k_\perp ^2 = k_y^2g^{yy} + 2k_xk_y g^{xy} + k_x^2 g^{xx}$![]() with the parallel coordinate $z$
with the parallel coordinate $z$![]() , which can have significant variation along the field line, whereas in the sheared slab, only the secular variation of $k_\perp ^2 =k_y^2(1 + z^2/L_s^2)$
, which can have significant variation along the field line, whereas in the sheared slab, only the secular variation of $k_\perp ^2 =k_y^2(1 + z^2/L_s^2)$![]() with $z$
with $z$![]() is present. This local variation of $k_\perp$
is present. This local variation of $k_\perp$![]() along the field line could give rise to the different dependence of universal modes on the wavenumbers $k_x$
along the field line could give rise to the different dependence of universal modes on the wavenumbers $k_x$![]() and $k_y$
and $k_y$![]() , allowing instability to occur at lower $k_y$
, allowing instability to occur at lower $k_y$![]() . Moreover, we note that the universal modes at the lowest $k_y\rho _s$
. Moreover, we note that the universal modes at the lowest $k_y\rho _s$![]() values seen here have a significant value of $k_x$
values seen here have a significant value of $k_x$![]() , further supplementing the magnitude, and parallel variation of $k_\perp$
, further supplementing the magnitude, and parallel variation of $k_\perp$![]() .
.
From examining the universal instability in these geometries, we conclude that the universal instability appears not only in devices which locally satisfy the maximum-$J$![]() property, like the high-mirror configuration of W7-X, but also in non-maximum-$J$
property, like the high-mirror configuration of W7-X, but also in non-maximum-$J$![]() devices. No such instabilities were found in tokamak geometry. We confirm that the presence of universal-instability drive is most distinct in locally maximum-$J$
devices. No such instabilities were found in tokamak geometry. We confirm that the presence of universal-instability drive is most distinct in locally maximum-$J$![]() devices by finding similar results to those in the high-mirror configuration of W7-X in the Quasi-Isodynamic Poloidally Closed stellarator (QIPC), which is even more quasi-isodynamic than the high-mirror configuration of W7-X (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov, Kalyuzhnyj and Cooper2006), see the Appendix.
devices by finding similar results to those in the high-mirror configuration of W7-X in the Quasi-Isodynamic Poloidally Closed stellarator (QIPC), which is even more quasi-isodynamic than the high-mirror configuration of W7-X (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov, Kalyuzhnyj and Cooper2006), see the Appendix.
5. Evidence of universal modes in nonlinear simulations in W7-X
To investigate how the linear universal modes identified at $0.15 \leq k_y\rho _s \leq 0.4$![]() in the high-mirror configuration of W7-X in § 4 translate to nonlinear simulations, we examine the nonlinear W7-X high-mirror simulations recently published by Proll et al. (Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). These simulations were carried out at a density gradient of $a/L_n =3$
in the high-mirror configuration of W7-X in § 4 translate to nonlinear simulations, we examine the nonlinear W7-X high-mirror simulations recently published by Proll et al. (Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). These simulations were carried out at a density gradient of $a/L_n =3$![]() , which facilitates comparison with the linear $a/L_n = 3$
, which facilitates comparison with the linear $a/L_n = 3$![]() results in § 4 while also being in the experimentally relevant density-gradient range.
results in § 4 while also being in the experimentally relevant density-gradient range.
In the nonlinear simulations, the parallel mode structure is dominated by the zonal flow in the high-mirror configuration of W7-X. In figure 11, the parallel mode structure of $\phi _{\rm NL}$![]() from the nonlinear simulation is compared with a linear universal eigenmode as well as the non-zonal $\phi _{{\rm NL},k_y \neq 0}$
from the nonlinear simulation is compared with a linear universal eigenmode as well as the non-zonal $\phi _{{\rm NL},k_y \neq 0}$![]() . We find strong agreement between the nonlinear, non-zonal mode structure $\phi _{{\rm NL},k_y \neq 0}$
. We find strong agreement between the nonlinear, non-zonal mode structure $\phi _{{\rm NL},k_y \neq 0}$![]() and the linear mode structure of the universal instability with the highest growth rate (not the highest growth rate of all simulated modes) at $k_y\rho _s = 0.3$
and the linear mode structure of the universal instability with the highest growth rate (not the highest growth rate of all simulated modes) at $k_y\rho _s = 0.3$![]() from the high-mirror configuration linear simulations. We also note the lack of similarity to the linear iTEM and TEM mode structures shown in figures 1 and 5, despite the iTEMs having substantially higher growth rates than any universal mode found in the high-mirror configuration of W7-X.
from the high-mirror configuration linear simulations. We also note the lack of similarity to the linear iTEM and TEM mode structures shown in figures 1 and 5, despite the iTEMs having substantially higher growth rates than any universal mode found in the high-mirror configuration of W7-X.

Figure 11. A comparison between the nonlinear electrostatic potential $|\phi _{\rm NL}|$![]() , the non-zonal ($k_y \neq 0$
, the non-zonal ($k_y \neq 0$![]() ) component of nonlinear electrostatic potential $|\phi _{{\rm NL},k_y \neq 0}|$
) component of nonlinear electrostatic potential $|\phi _{{\rm NL},k_y \neq 0}|$![]() and the fastest growing universal mode in the high-mirror configuration of W7-X at $k_y\rho _s = 0.3$
and the fastest growing universal mode in the high-mirror configuration of W7-X at $k_y\rho _s = 0.3$![]() , where all three curves have been normalised to their maximum amplitude.
, where all three curves have been normalised to their maximum amplitude.
In figure 12, the normalised mode structures for $k_y\rho _s \leq 0.5$![]() indicate that the universal instability appears nonlinearly in the same $k_y$
indicate that the universal instability appears nonlinearly in the same $k_y$![]() range at which it was identified in linear simulations (see figure 2). Above this range, the observed modes have a large central peak at $z = 0$
range at which it was identified in linear simulations (see figure 2). Above this range, the observed modes have a large central peak at $z = 0$![]() , which does not match the expected mode structure of the linear iTEM seen at these $k_y$
, which does not match the expected mode structure of the linear iTEM seen at these $k_y$![]() scales in figure 1. It is likely that the universal instability dominates the overall mode structure because it appears in a nonlinearly relevant $k_y\rho _s$
scales in figure 1. It is likely that the universal instability dominates the overall mode structure because it appears in a nonlinearly relevant $k_y\rho _s$![]() range, as can be seen in figure 12(b), where the $\phi _{\rm NL}$
range, as can be seen in figure 12(b), where the $\phi _{\rm NL}$![]() amplitude is largest.
amplitude is largest.

Figure 12. Results from nonlinear simulations in W7-X high-mirror. (a) Parallel structures of the electrostatic potential $|\phi _{\rm NL}|$![]() in the nonlinear simulations, as a function of $k_y\rho _s$
in the nonlinear simulations, as a function of $k_y\rho _s$![]() and normalised to the maximum amplitude of each mode, visualised as a heatmap. The density perturbation $n(z)$
and normalised to the maximum amplitude of each mode, visualised as a heatmap. The density perturbation $n(z)$![]() (not shown) exhibits the same features. (b) Amplitude spectrum of the electrostatic potential as a function of $k_y\rho _s$
(not shown) exhibits the same features. (b) Amplitude spectrum of the electrostatic potential as a function of $k_y\rho _s$![]() , showing a large zonal ($k_y= 0$
, showing a large zonal ($k_y= 0$![]() ) component. In panel (a), the broad universal mode structure is visible for $k_y\rho _s < 0.5$
) component. In panel (a), the broad universal mode structure is visible for $k_y\rho _s < 0.5$![]() , which is also where $|\phi _{\rm NL}|$
, which is also where $|\phi _{\rm NL}|$![]() is largest in panel (b), excluding the zonal component.
is largest in panel (b), excluding the zonal component.
Interestingly, the recent results of Proll et al. (Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022) indicate that the destabilisation of universal modes, which occurs at $a/L_n = 2$![]() in the high-mirror configuration of W7-X, is associated with a decrease in the turbulent heat flux in this configuration. This turbulence mitigation with increasing density gradient may have been connected to an enhanced zonal-flow response which appears after the onset of the universal instability. The improved zonal-flow generation may be a result of the large change of turbulence localisation as the universal modes begin to dominate the nonlinear mode structure, as more extended mode structures have been shown to generate zonal flows more efficiently than more peaked instabilities (Plunk, Xanthopoulos & Helander Reference Plunk, Xanthopoulos and Helander2017b). Further work is needed to understand the implications of the dominance of the universal instability in nonlinear turbulence in W7-X and its effect on zonal flow generation. Studies of this nature performed in HSX by Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015) found that zonal flows may have a more important role in turbulence saturation in a low-shear device than would be expected in a comparable device with large shear.
in the high-mirror configuration of W7-X, is associated with a decrease in the turbulent heat flux in this configuration. This turbulence mitigation with increasing density gradient may have been connected to an enhanced zonal-flow response which appears after the onset of the universal instability. The improved zonal-flow generation may be a result of the large change of turbulence localisation as the universal modes begin to dominate the nonlinear mode structure, as more extended mode structures have been shown to generate zonal flows more efficiently than more peaked instabilities (Plunk, Xanthopoulos & Helander Reference Plunk, Xanthopoulos and Helander2017b). Further work is needed to understand the implications of the dominance of the universal instability in nonlinear turbulence in W7-X and its effect on zonal flow generation. Studies of this nature performed in HSX by Faber et al. (Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015) found that zonal flows may have a more important role in turbulence saturation in a low-shear device than would be expected in a comparable device with large shear.
6. Conclusions
We have presented evidence of the existence of the passing-electron-driven universal instability in stellarator geometries. This instability is readily identifiable in the high-mirror configuration of W7-X due to the reduced growth rates of the TEM as a consequence of the maximum-$J$![]() property possessed by deeply trapped particles in the region of worst curvature. The presence of classical TEMs in the non-maximum-$J$
property possessed by deeply trapped particles in the region of worst curvature. The presence of classical TEMs in the non-maximum-$J$![]() geometries, W7-X negative-mirror and HSX, made the universal instability more difficult to detect. It was only present in isolation from the TEM at a single simulated $k_y$
geometries, W7-X negative-mirror and HSX, made the universal instability more difficult to detect. It was only present in isolation from the TEM at a single simulated $k_y$![]() in the negative-mirror configuration. In HSX, universal modes were found to be indistinguishable from TEMs based on their mode structure alone, with identification requiring phase angle analyses for passing and trapped electrons. Despite this, modes, primarily driven by passing electrons, dominate at the largest scales in HSX, although their distinction from the TEM is difficult as trapped electrons may also contribute significantly to the growth of these modes in HSX. The appearance of the universal instability in HSX may seem inconsequential at first, given that the mode structure, and therefore turbulence localisation, is the same as what would be anticipated from the TEM, but for optimisation and nonlinear turbulence studies, it is an important consideration given that universal modes have been demonstrated to give rise to subcritical turbulence nonlinearly in slab simulations (Landreman et al. Reference Landreman, Plunk and Dorland2015b). In both HSX and the negative-mirror configuration of W7-X, we find that TEM and universal mode branches are not very distinct, such that hybrid universal–TEM modes are more likely to be the dominant instability at low $k_y$
in the negative-mirror configuration. In HSX, universal modes were found to be indistinguishable from TEMs based on their mode structure alone, with identification requiring phase angle analyses for passing and trapped electrons. Despite this, modes, primarily driven by passing electrons, dominate at the largest scales in HSX, although their distinction from the TEM is difficult as trapped electrons may also contribute significantly to the growth of these modes in HSX. The appearance of the universal instability in HSX may seem inconsequential at first, given that the mode structure, and therefore turbulence localisation, is the same as what would be anticipated from the TEM, but for optimisation and nonlinear turbulence studies, it is an important consideration given that universal modes have been demonstrated to give rise to subcritical turbulence nonlinearly in slab simulations (Landreman et al. Reference Landreman, Plunk and Dorland2015b). In both HSX and the negative-mirror configuration of W7-X, we find that TEM and universal mode branches are not very distinct, such that hybrid universal–TEM modes are more likely to be the dominant instability at low $k_y$![]() in these geometries.
in these geometries.
We have found that because the universal mode is dominant at low $k_y$![]() , nonlinearly relevant scales in the high-mirror configuration of W7-X, it dominates the non-zonal component of the saturated mode structure in nonlinear simulations. This may have implications for the nature of density-gradient-driven turbulence in W7-X, as the parallel structure of the universal instability differs significantly from that of a TEM and may impact turbulence localisation in experiments. Moreover, the large extended parallel structure of these modes may allow for more efficient generation of zonal flows, as such extended modes have been found in other contexts (ion-temperature gradient turbulence) to couple more efficiently to zonal flows and damped modes nonlinearly (Faber et al. Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015; Plunk et al. Reference Plunk, Xanthopoulos and Helander2017b), leading to a reduction in turbulent heat flux.
, nonlinearly relevant scales in the high-mirror configuration of W7-X, it dominates the non-zonal component of the saturated mode structure in nonlinear simulations. This may have implications for the nature of density-gradient-driven turbulence in W7-X, as the parallel structure of the universal instability differs significantly from that of a TEM and may impact turbulence localisation in experiments. Moreover, the large extended parallel structure of these modes may allow for more efficient generation of zonal flows, as such extended modes have been found in other contexts (ion-temperature gradient turbulence) to couple more efficiently to zonal flows and damped modes nonlinearly (Faber et al. Reference Faber, Pueschel, Proll, Xanthopoulos, Terry, Hegna, Weir, Likin and Talmadge2015; Plunk et al. Reference Plunk, Xanthopoulos and Helander2017b), leading to a reduction in turbulent heat flux.
However, to be truly experimentally relevant, the impact of finite temperature gradients on these universal modes must be determined: in particular, the impact of the presence of ITGs on the nonlinear dominance of universal modes must be established, given that ITGs are often found to have considerable linear growth rates at the same $k_y$![]() values at which we observe the universal modes. It is worth noting that the inclusion of finite temperature gradients, which enters via $\eta _e$
values at which we observe the universal modes. It is worth noting that the inclusion of finite temperature gradients, which enters via $\eta _e$![]() in (2.12), will impact the linear growth of universal modes. Furthermore, it remains to be seen how these results translate to the global setting, where the stabilisation of the TEM due to the local maximum-$J$
in (2.12), will impact the linear growth of universal modes. Furthermore, it remains to be seen how these results translate to the global setting, where the stabilisation of the TEM due to the local maximum-$J$![]() property does not appear to be as effective, as shown by Riemann et al. (Reference Riemann, Kleiber, Borchardt and Slaby2022), where they find that the classic electron-driven TEM is robustly unstable in global simulations performed using EUTERPE (Jost et al. Reference Jost, Tran, Cooper, Villard and Appert2001) in the high-mirror configuration of W7-X with realistic temperature and density profiles. Interestingly, Riemann et al. (Reference Riemann, Kleiber, Borchardt and Slaby2022) also find electron-driven instabilities which are extended along the field line with a maximum at the outboard side of the bean-shaped cross-section, which corresponds to $z=0$
property does not appear to be as effective, as shown by Riemann et al. (Reference Riemann, Kleiber, Borchardt and Slaby2022), where they find that the classic electron-driven TEM is robustly unstable in global simulations performed using EUTERPE (Jost et al. Reference Jost, Tran, Cooper, Villard and Appert2001) in the high-mirror configuration of W7-X with realistic temperature and density profiles. Interestingly, Riemann et al. (Reference Riemann, Kleiber, Borchardt and Slaby2022) also find electron-driven instabilities which are extended along the field line with a maximum at the outboard side of the bean-shaped cross-section, which corresponds to $z=0$![]() in our simulations, and could be related to the universal modes we find here.
in our simulations, and could be related to the universal modes we find here.
The dominance of universal modes at lower-than-expected $k_y$![]() in stellarators warrants future investigation, particularly surrounding the impact of local variations of $k_\perp (z)$
in stellarators warrants future investigation, particularly surrounding the impact of local variations of $k_\perp (z)$![]() along the magnetic field on the slab geometry $k_y \rho _i > 0.7$
along the magnetic field on the slab geometry $k_y \rho _i > 0.7$![]() instability threshold established by Landreman et al. (Reference Landreman, Antonsen and Dorland2015a). Furthermore, the implications of the prevalence of this instability nonlinearly must be explored more deeply.
instability threshold established by Landreman et al. (Reference Landreman, Antonsen and Dorland2015a). Furthermore, the implications of the prevalence of this instability nonlinearly must be explored more deeply.
Finally, we note the possibility that universal modes may be of relevance to density-gradient-driven turbulence in the new, more precisely quasi-symmetric and quasi-isodynamic devices shown by Landreman & Paul (Reference Landreman and Paul2022) and Goodman et al. (Reference Goodman, Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach and Helander2022), which appear to favour near-zero magnetic shear. Universal instabilities may also become a prominent instability as a result of directly optimising stellarators for reduced TEM growth rates by reducing the available energy of trapped electrons in the device (Mackenbach, Proll & Helander Reference Mackenbach, Proll and Helander2022).
Acknowledgements
The authors thank M. Morren, P. Mulholland, R. Mackenbach and A. von Stechow for useful conversations during the course of this work.
Editor William Dorland thanks the referees for their advice in evaluating this article.
Declaration of interest
The authors report no conflict of interest.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Programme (Grant Agreement No. 101052200 – EUROfusion). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Data availability statement
Relevant data which aid in reproducing the findings of this work, such as input files for simulations, are available upon request.
Appendix. A more quasi-isodynamic configuration
The Quasi-Isodynamic Poloidally Closed (QIPC) stellarator represents an even better approximation of a perfectly quasi-isodynamic device than the high-mirror configuration of W7-X. As a result, it enjoys even better stabilisation of TEMs (Proll et al. Reference Proll, Xanthopoulos and Helander2013). We would therefore expect that universal modes would be more prevalent in this geometry thanks to the further reduction in the growth of TEMs. In the simulation results in QIPC, we see similar behaviour to that observed in W7-X high-mirror. However, unlike in W7-X, no electron-driven TEMs are observed, only iTEMs are found for $k_y\rho _s > 0.3$![]() . These iTEMs, seen in figure 13, have the expected mode structure of peaking in the few regions where $\mathcal {K}_2 <0$
. These iTEMs, seen in figure 13, have the expected mode structure of peaking in the few regions where $\mathcal {K}_2 <0$![]() and magnetic minima overlap, particularly at the edge of the simulation domain. The absence of dominant electron-driven TEMs indicates the closeness to which QIPC approximates quasi-isodynamicity and satisfies the maximum-$J$
and magnetic minima overlap, particularly at the edge of the simulation domain. The absence of dominant electron-driven TEMs indicates the closeness to which QIPC approximates quasi-isodynamicity and satisfies the maximum-$J$![]() criterion for a larger portion of the trapped-particle population. This device also has very low magnetic shear with $\hat {s}_{\text {QIPC}} = -0.0248939$
criterion for a larger portion of the trapped-particle population. This device also has very low magnetic shear with $\hat {s}_{\text {QIPC}} = -0.0248939$![]() , giving a value of $(L_s/L_n)_{\text {QIPC},3} \approx 1640$
, giving a value of $(L_s/L_n)_{\text {QIPC},3} \approx 1640$![]() .
.

Figure 13. Parallel structure of linear $|\phi|$![]() eigenmodes in QIPC. Shown are an iTEM at $k_y\rho _s = 1$
eigenmodes in QIPC. Shown are an iTEM at $k_y\rho _s = 1$![]() and a universal mode at $k_y\rho _s = 0.3$
and a universal mode at $k_y\rho _s = 0.3$![]() , alongside the magnetic field strength $B(z)$
, alongside the magnetic field strength $B(z)$![]() and the curvature $\mathcal {K}_2$
and the curvature $\mathcal {K}_2$![]() .
.
In this geometry, we find a mode branch that exhibits the same properties as the universal instability mode branch observed in the W7-X high-mirror configuration. In QIPC, these modes are found for $0.05 \leq k_y\rho _s \leq 0.3$![]() . The universal modes found in QIPC are distinct from iTEMs in mode structure, as shown in figure 13. These universal modes peak predominantly in regions of maximal $B(z)$
. The universal modes found in QIPC are distinct from iTEMs in mode structure, as shown in figure 13. These universal modes peak predominantly in regions of maximal $B(z)$![]() and bad curvature, which often overlap in QIPC. This further highlights the passing particle nature of these universal instability modes. Once more, we find that universal modes exhibit a distinct frequency and growth rate branch in figure 14(a), and are indicated by a low overall cross-phase with $n_{\rm pass}$
and bad curvature, which often overlap in QIPC. This further highlights the passing particle nature of these universal instability modes. Once more, we find that universal modes exhibit a distinct frequency and growth rate branch in figure 14(a), and are indicated by a low overall cross-phase with $n_{\rm pass}$![]() being slightly less in-phase than $n_{\rm trap}$
being slightly less in-phase than $n_{\rm trap}$![]() , as seen in figure 14(b). Interestingly, despite the increase in TEM stability in QIPC, which is owed to its closer approximation of perfect quasi-isodynamicity, we do not observe universal instability modes over a larger range in $k_y\rho _s$
, as seen in figure 14(b). Interestingly, despite the increase in TEM stability in QIPC, which is owed to its closer approximation of perfect quasi-isodynamicity, we do not observe universal instability modes over a larger range in $k_y\rho _s$![]() as one might expect. This may be due to an even more pronounced stabilising effect of trapped electrons in this more highly maximum-$J$
as one might expect. This may be due to an even more pronounced stabilising effect of trapped electrons in this more highly maximum-$J$![]() geometry, or a larger population of trapped electrons due to the higher mirror ratio of this device.
geometry, or a larger population of trapped electrons due to the higher mirror ratio of this device.

Figure 14. Results from linear simulations in QIPC. (a) Frequencies $\omega$![]() and growth rates $\gamma$
and growth rates $\gamma$![]() , displaying a negative $\omega$
, displaying a negative $\omega$![]() universal mode branch at low-$k_y$
universal mode branch at low-$k_y$![]() , with all other modes being iTEMs with frequency in the ion-diamagnetic direction. (b) Cross-phases $\alpha$
, with all other modes being iTEMs with frequency in the ion-diamagnetic direction. (b) Cross-phases $\alpha$![]() between the electrostatic potential $\phi$
between the electrostatic potential $\phi$![]() and the trapped and passing electron density perturbations, with the universal mode signature of almost in-phase $n_{\rm trap}$
and the trapped and passing electron density perturbations, with the universal mode signature of almost in-phase $n_{\rm trap}$![]() and $n_{\rm pass}$
and $n_{\rm pass}$![]() evident at low-$k_y$
evident at low-$k_y$![]() .
.