No CrossRef data available.
Published online by Cambridge University Press: 19 December 2018
Spacecraft measurements of propagating interplanetary shocks are often interpreted using the ideal magnetohydrodynamic (MHD) model of a planar shock wave travelling with constant velocity 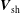 $\boldsymbol{V}_{\text{sh}}$ through a spatially uniform plasma. In particular, measurements of the plasma variables upstream and downstream have long been used in conjunction with the Rankine–Hugoniot conditions, also known as the MHD jump conditions, to determine shock velocities and other physical parameters of interplanetary shocks. This procedure is justified only if the shock velocity determined by the MHD jump conditions is unique. In this study the important property of uniqueness is demonstrated for non-perpendicular shocks in MHD media characterized by an isotropic pressure tensor. The primary conclusion is that the shock velocity is uniquely determined by the jump conditions regardless of the type of shock (slow, intermediate or fast). Several new formulas for the shock speed are also derived including one that is independent of the shock normal
$\boldsymbol{V}_{\text{sh}}$ through a spatially uniform plasma. In particular, measurements of the plasma variables upstream and downstream have long been used in conjunction with the Rankine–Hugoniot conditions, also known as the MHD jump conditions, to determine shock velocities and other physical parameters of interplanetary shocks. This procedure is justified only if the shock velocity determined by the MHD jump conditions is unique. In this study the important property of uniqueness is demonstrated for non-perpendicular shocks in MHD media characterized by an isotropic pressure tensor. The primary conclusion is that the shock velocity is uniquely determined by the jump conditions regardless of the type of shock (slow, intermediate or fast). Several new formulas for the shock speed are also derived including one that is independent of the shock normal 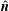 $\hat{\boldsymbol{n}}$. In principle, the solution technique developed here can be applied to estimate
$\hat{\boldsymbol{n}}$. In principle, the solution technique developed here can be applied to estimate 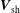 $\boldsymbol{V}_{\text{sh}}$ using solar wind data provided the measurements obey the MHD shock model with sufficient accuracy. That is not its intended purpose, however, and such applications are beyond the scope of this work.
$\boldsymbol{V}_{\text{sh}}$ using solar wind data provided the measurements obey the MHD shock model with sufficient accuracy. That is not its intended purpose, however, and such applications are beyond the scope of this work.