Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T21:21:16.553Z Has data issue: false hasContentIssue false
  • English
  • Français

Stabilisation of short-wavelength instabilities by parallel-to-the-field shear in long-wavelength E × B flows

Part of: Focus on Fusion

Published online by Cambridge University Press:  09 November 2020

M. R. Hardman Open the ORCID record for M. R. Hardman [Opens in a new window] ,
M. Barnes Open the ORCID record for M. Barnes [Opens in a new window]  and
C. M. Roach Open the ORCID record for C. M. Roach [Opens in a new window]
M. R. Hardman*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK Culham Centre for Fusion Energy, UKAEA, AbingdonOX14 3DB, UK
M. Barnes
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, OxfordOX1 3PU, UK
C. M. Roach
Affiliation:
Culham Centre for Fusion Energy, UKAEA, AbingdonOX14 3DB, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Magnetised plasma turbulence can have a multiscale character: instabilities driven by mean temperature gradients drive turbulence at the disparate scales of the ion and the electron gyroradii. Simulations of multiscale turbulence, using equations valid in the limit of infinite scale separation, reveal novel cross-scale interaction mechanisms in these plasmas. In the case that both long-wavelength (ion-gyroradius-scale) and short-wavelength (electron-gyroradius-scale) linear instabilities are driven far from marginal stability, we show that the short-wavelength instabilities are suppressed by interactions with long-wavelength turbulence. Two novel effects contributed to the suppression: parallel-to-the-field-line shearing by the long-wavelength 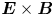${{\boldsymbol {E}} \times \boldsymbol {B}}$ flows, and the modification of the background density gradient by the piece of the long-wavelength electron adiabatic response with parallel-to-the-field-line variation. In contrast, simulations of multiscale turbulence where instabilities at both scales are driven near marginal stability demonstrate that when the long-wavelength turbulence is sufficiently collisional and zonally dominated the effect of cross-scale interaction can be parameterised solely in terms of the local modifications to the mean density and temperature gradients. We discuss physical arguments that qualitatively explain how a change in equilibrium drive leads to the observed transition in the impact of the cross-scale interactions.

Keywords

plasma nonlinear phenomenaplasma simulationfusion plasma
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 6 , December 2020 , 905860601
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abel, I. G., Plunk, G. G., Wang, E., Barnes, M., Cowley, S. C., Dorland, W. & Schekochihin, A. A. 2013 Multiscale gyrokinetics for rotating tokamak plasmas: fluctuations, transport, and energy flows. Rep. Prog. Phys. 76, 116201.CrossRefGoogle ScholarPubMed
Adam, J. C., Tang, W. M. & Rutherford, P. H. 1976 Destabilization of the trapped-electron mode by magnetic curvature drift resonances. Phys. Fluids 19, 561–566.CrossRefGoogle Scholar
Barnes, M., Dorland, W. & Tatsuno, T. 2010 Resolving velocity space dynamics in continuum gyrokinetics. Phys. Plasmas 17, 032106.CrossRefGoogle Scholar
Barnes, M., Parra, F. I. & Schekochihin, A. A. 2011 Critically balanced ion temperature gradient turbulence in fusion plasmas. Phys. Rev. Lett. 107, 115003.CrossRefGoogle ScholarPubMed
Bonanomi, N., Mantica, P., Citrin, J., Görler, T., Teaca, B. & JET Contributors 2018 Impact of electron-scale turbulence and multi-scale interactions in the JET tokamak. Nucl. Fusion 58, 124003.CrossRefGoogle Scholar
Brizard, A. J. & Hahm, T. S. 2007 Foundations of nonlinear gyrokinetic theory. Rev. Mod. Phys. 79, 421–468.CrossRefGoogle Scholar
Candy, J., Waltz, R. E., Fahey, M. R. & Holland, C. 2007 The effect of ion-scale dynamics on electron-temperature-gradient turbulence. Plasma Phys. Control. Fusion 49, 1209–1220.CrossRefGoogle Scholar
Catto, P. J. 1978 Linearized gyro-kinetics. Plasma Phys. 20, 719–722.CrossRefGoogle Scholar
Cowley, S. C., Kulsrud, R. M. & Sudan, R. 1991 Considerations of ion-temperature-gradient-driven turbulence. Phys. Fluids B 3, 2767–2782.CrossRefGoogle Scholar
Creely, A. J., Rodriguez-Fernandez, P., Conway, G. D., Freethy, S. J., Howard, N. T., White, A. E. & the ASDEX Upgrade Team 2019 Criteria for the importance of multi-scale interactions in turbulent transport simulations. Plasma Phys. Control. Fusion 61, 085022.CrossRefGoogle Scholar
Dimits, A. M., Bateman, G., Beer, M. A., Cohen, B. I., Dorland, W., Hammett, G. W., Kim, C., Kinsey, J. E., Kotschenreuther, M., Kritz, A. H., et al. 2000 Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 7, 969–983.CrossRefGoogle Scholar
Dorland, W., Jenko, F., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient turbulence. Phys. Rev. Lett. 85, 5579–5582.CrossRefGoogle ScholarPubMed
Frieman, E. A. & Chen, L. 1982 Nonlinear gyrokinetic equations for low-frequency electromagnetic waves in general plasma equilibria. Phys. Fluids 25, 502–508.CrossRefGoogle Scholar
Görler, T. & Jenko, F. 2008 Scale separation between electron and ion thermal transport. Phys. Rev. Lett. 100, 185002.CrossRefGoogle ScholarPubMed
Hardman, M. 2019 Multiscale turbulence in magnetic confinement fusion devices. PhD thesis, University of Oxford.Google Scholar
Hardman, M. R., Barnes, M., Roach, C. M. & Parra, F. I. 2019 A scale-separated approach for studying coupled ion and electron scale turbulence. Plasma Phys. Control. Fusion 61, 065025.CrossRefGoogle Scholar
Hildebrand, F. B. 1987 Introduction to Numerical Analysis, 2nd edn. Dover.Google Scholar
Horton, W., Hong, B. G. & Tang, W. M. 1988 Toroidal electron temperature gradient driven drift modes. Phys. Fluids 31, 2971–2983.CrossRefGoogle Scholar
Howard, N. T., Holland, C., White, A. E., Greenwald, M. & Candy, J. 2014 Synergistic cross-scale coupling of turbulence in a tokamak plasma. Phys. Plasmas 21, 112510.CrossRefGoogle Scholar
Howard, N. T., Holland, C., White, A. E., Greenwald, M. & Candy, J. 2015 Fidelity of reduced and realistic electron mass ratio multi-scale gyrokinetic simulations of tokamak discharges. Plasma Phys. Control. Fusion 57, 065009.CrossRefGoogle Scholar
Howard, N. T., Holland, C., White, A. E., Greenwald, M. & Candy, J. 2016 a Multi-scale gyrokinetic simulation of tokamak plasmas: enhanced heat loss due to cross-scale coupling of plasma turbulence. Nucl. Fusion 56, 014004.CrossRefGoogle Scholar
Howard, N. T., Holland, C., White, A. E., Greenwald, M., Candy, J. & Creely, A. J. 2016 b Multi-scale gyrokinetic simulations: comparison with experiment and implications for predicting turbulence and transport. Phys. Plasmas 23, 056109.CrossRefGoogle Scholar
Itoh, S.-I. & Itoh, K. 2001 Statistical theory and transition in multiple-scale-length turbulence in plasmas. Plasma Phys. Control. Fusion 43, 1055–1102.CrossRefGoogle Scholar
Jenko, F. & Dorland, W. 2002 Prediction of significant tokamak turbulence at electron gyroradius scales. Phys. Rev. Lett. 89, 225001.CrossRefGoogle ScholarPubMed
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7, 1904–1910.CrossRefGoogle Scholar
Kotschenreuther, M., Rewoldt, G. & Tang, W. 1995 Comparison of initial value and eigenvalue codes for kinetic toroidal plasma instabilities. Comput. Phys. Commun. 88, 128–140.CrossRefGoogle Scholar
Lee, Y. C., Dong, J. Q., Guzdar, P. N. & Liu, C. S. 1987 Collisionless electron temperature gradient instability. Phys. Fluids 30, 1331–1339.CrossRefGoogle Scholar
Maeyama, S., Idomura, Y., Watanabe, T.-H., Nakata, M., Yagi, M., Miyato, N., Ishizawa, A. & Nunami, M. 2015 Cross-scale interactions between electron and ion scale turbulence in a tokamak plasma. Phys. Rev. Lett. 114, 255002.CrossRefGoogle Scholar
Maeyama, S., Watanabe, T.-H., Idomura, Y., Nakata, M., Ishizawa, A. & Nunami, M. 2017 a Cross-scale interactions between turbulence driven by electron and ion temperature gradients via sub-ion-scale structures. Nucl. Fusion 57, 066036.CrossRefGoogle Scholar
Maeyama, S., Watanabe, T.-H. & Ishizawa, A. 2017 b Suppression of ion-scale microtearing modes by electron-scale turbulence via cross-scale nonlinear interactions in tokamak plasmas. Phys. Rev. Lett. 119, 195002.CrossRefGoogle ScholarPubMed
Parisi, J. F., Parra, F. I., Roach, C. M., Giroud, C., Dorland, W., Hatch, D. R., Barnes, M., Hillesheim, J. C., Aiba, N., Ball, J., et al. 2020 Toroidal and slab ETG instability dominance in the linear spectrum of JET-ILW pedestals. Nucl. Fusion 60, 126045.CrossRefGoogle Scholar
Roach, C. M., Abel, I. G., Akers, R. J., Arter, W., Barnes, M., Camenen, Y., Casson, F. J., Colyer, G., Connor, J. W., Cowley, S. C., et al. 2009 Gyrokinetic simulations of spherical tokamaks. Plasma Phys. Control. Fusion 51, 124020.CrossRefGoogle Scholar
Rogers, B. N., Dorland, W. & Kotschenreuther, M. 2000 Generation and stability of zonal flows in ion-temperature-gradient mode turbulence. Phys. Rev. Lett. 85, 5336–5339.CrossRefGoogle ScholarPubMed
Romanelli, F. 1989 Ion temperature-gradient-driven modes and anomalous ion transport in tokamaks. Phys. Fluids B 1, 1018–1025.CrossRefGoogle Scholar
Smith, S. A. 1997Dissipative closures for statistical moments, fluid moments, and subgrid scales in plasma turbulence. PhD thesis, Princeton University.Google Scholar
Staebler, G. M., Candy, J., Howard, N. T. & Holland, C. 2016 The role of zonal flows in the saturation of multi-scale gyrokinetic turbulence. Phys. Plasmas 23, 062518.CrossRefGoogle Scholar
Staebler, G. M., Howard, N. T., Candy, J. & Holland, C. 2017 A model of the saturation of coupled electron and ion scale gyrokinetic turbulence. Nucl. Fusion 57, 066046.CrossRefGoogle Scholar
Sugama, H. & Horton, W. 1997 Transport processes and entropy production in toroidally rotating plasmas with electrostatic turbulence. Phys. Plasmas 4, 405–418.CrossRefGoogle Scholar
Waltz, R. E., Candy, J. & Fahey, M. 2007 Coupled ion temperature gradient and trapped electron mode to electron temperature gradient mode gyrokinetic simulations. Phys. Plasmas 14, 056116.CrossRefGoogle Scholar