Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-29T14:53:21.889Z Has data issue: false hasContentIssue false
  • English
  • Français

A solvable model of Vlasov-kinetic plasma turbulence in Fourier–Hermite phase space

Published online by Cambridge University Press:  25 January 2018

T. Adkins  and
A. A. Schekochihin
T. Adkins
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK Merton College, Merton Street, Oxford OX1 4JD, UK
A. A. Schekochihin*
Affiliation:
Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK Merton College, Merton Street, Oxford OX1 4JD, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A class of simple kinetic systems is considered, described by the one-dimensional Vlasov–Landau equation with Poisson or Boltzmann electrostatic response and an energy source. Assuming a stochastic electric field, a solvable model is constructed for the phase-space turbulence of the particle distribution. The model is a kinetic analogue of the Kraichnan–Batchelor model of chaotic advection. The solution of the model is found in Fourier–Hermite space and shows that the free-energy flux from low to high Hermite moments is suppressed, with phase mixing cancelled on average by anti-phase-mixing (stochastic plasma echo). This implies that Landau damping is an ineffective route to dissipation (i.e. to thermalisation of electric energy via velocity space). The full Fourier–Hermite spectrum is derived. 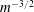Its asymptotics are $m^{-3/2}$ at low wavenumbers and high Hermite moments (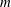$m$) and $m^{-1/2}k^{-2}$ at low Hermite moments and high wavenumbers ($k$). These conclusions hold at wavenumbers below a certain cutoff (analogue of Kolmogorov scale), which increases with the amplitude of the stochastic electric field and scales as inverse square of the collision rate. The energy distribution and flows in phase space are a simple and, therefore, useful example of competition between phase mixing and nonlinear dynamics in kinetic turbulence, reminiscent of more realistic but more complicated multi-dimensional systems that have not so far been amenable to complete analytical solution.

Keywords

plasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 1 , February 2018 , 905840107
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonsen, T. M. Jr., Fan, Z., Ott, E & Garcia-Lopez, E. 1996 The role of chaotic orbits in the determination of power spectra of passive scalars. Phys. Fluids 8, 3094.CrossRefGoogle Scholar
Bañón Navarro, A., Morel, P., Albrecht-Marc, M., Carati, D., Merz, F., Görler, T. & Jenko, F. 2011 Free energy cascade in gyrokinetic turbulence. Phys. Rev. Lett. 106, 055001.CrossRefGoogle ScholarPubMed
Batchelor, G. K. 1959 Small-scale variation of convected quantities like temperature in turbulent fluid. Part 1. General discussion and the case of small conductivity. J. Fluid Mech. 5, 113.Google Scholar
Beer, M. A. & Hammett, G. W. 1996 Toroidal gyrofluid equations for simulations of tokamak turbulence. Phys. Plasmas 3, 4046.CrossRefGoogle Scholar
Bernstein, I. B., Greene, J. M. & Kruskal, M. D. 1957 Exact nonlinear plasma oscillations. Phys. Rev. 108, 546.CrossRefGoogle Scholar
Bhat, P. & Subramanian, K. 2015 Fluctuation dynamos at finite correlation times using renewing flows. J. Plasma Phys. 81, 395810502.CrossRefGoogle Scholar
Boldyrev, S. & Cattaneo, F. 2004 Magnetic-field generation in Kolmogorov turbulence. Phys. Rev. Lett. 92, 144501.Google Scholar
Cook, I. 1978 Application of the Novikov-Furutsu theorem to the random acceleration problem. Plasma Phys. 20, 349.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dorland, W. & Hammett, G. W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B 5, 812.Google Scholar
Dupree, T. H. 1972 Theory of phase space density granulation in plasma. Phys. Fluids 15, 334.CrossRefGoogle Scholar
Falkovich, G., Gawȩdzki, K. & Vergassola, M. 2001 Particles and fields in fluid turbulence. Rev. Mod. Phys. 73, 913.Google Scholar
Furutsu, K. 1963 On the statistical theory of electromagnetic waves in a fluctuating medium (I). J. Res. Natl Bur. Stand. 67D, 303.Google Scholar
Goldman, M. V. 1984 Strong turbulence of plasma waves. Rev. Mod. Phys. 56, 709.Google Scholar
Goswami, P., Passot, T. & Sulem, P. L. 2005 A Landau fluid model for warm collisionless plasmas. Phys. Plasmas 12, 102109.CrossRefGoogle Scholar
Gould, R. W., O’Neil, T. M. & Malmberg, J. H. 1967 Plasma wave echo. Phys. Rev. Lett. 19, 219.CrossRefGoogle Scholar
Hammett, G. W., Beer, M. A., Dorland, W., Cowley, S. C. & Smith, S. A. 1993 Developments in the gyrofluid approach to tokamak turbulence simulations. Plasma Phys. Control. Fusion 35, 973.CrossRefGoogle Scholar
Hammett, G. W., Dorland, W. & Perkins, F. W. 1992 Fluid models of phase mixing, Landau damping, and nonlinear gyrokinetic dynamics. Phys. Fluids B 4, 2052.CrossRefGoogle Scholar
Hammett, G. W. & Perkins, F. W. 1990 Fluid moment models for Landau damping with application to the ion-temperature-gradient instability. Phys. Rev. Lett. 64, 3019.CrossRefGoogle Scholar
Hatch, D. R., Jenko, F., Bratanov, V. & Bañón Navarro, A. 2014 Phase space scales of free energy dissipation in gradient-driven gyrokinetic turbulence. J. Plasma Phys. 80, 531.CrossRefGoogle Scholar
Howes, G. G., Klein, K. G. & Li, T. C. 2017 Diagnosing collisionless energy transfer using field-particle correlations: Vlasov–Poisson plasmas. J. Plasma Phys. 83, 705830102.CrossRefGoogle Scholar
Kanekar, A., Schekochihin, A. A., Dorland, W. & Loureiro, N. F. 2015 Fluctuation-dissipation relations for a plasma-kinetic Langevin equation. J. Plasma Phys. 81, 305810104.Google Scholar
Kanekar, A. V.2015 Phase mixing in turbulent magnetized plasmas. PhD thesis, University of Maryland, College Park (URL: http://drum.lib.umd.edu/handle/1903/16418).Google Scholar
Kawamori, E. 2013 Experimental verification of entropy cascade in two-dimensional electrostatic turbulence in magnetized plasma. Phys. Rev. Lett. 110, 095001.CrossRefGoogle ScholarPubMed
Kazantsev, A. P. 1968 Enhancement of a magnetic field by a conducting fluid. Sov. Phys. JETP 26, 1031.Google Scholar
Kingsep, A. S. 2004 Introduction to Nonlinear Plasma Physics. MZ Press (in Russian).Google Scholar
Klein, K. G., Howes, G. G. & Tenbarge, J. M. 2017 Diagnosing collisionless energy transfer using field-particle correlations: gyrokinetic turbulence. J. Plasma Phys. 83, 535830401.CrossRefGoogle Scholar
Knorr, G. 1977 Time asymptotic statistics of the Vlasov equation. J. Plasma Phys. 17, 553.CrossRefGoogle Scholar
Kosuga, Y. & Diamond, P. H. 2011 On relaxation and transport in gyrokinetic drift wave turbulence with zonal flow. Phys. Plasmas 18, 122305.Google Scholar
Kosuga, Y., Itoh, S.-I., Diamond, P. H., Itoh, K. & Lesur, M. 2014 Ion temperature gradient driven turbulence with strong trapped ion resonance. Phys. Plasmas 21, 102303.Google Scholar
Kosuga, Y., Itoh, S.-I., Diamond, P. H., Itoh, K. & Lesur, M. 2017 Role of phase space structures in collisionless drift wave turbulence and impact on transport modeling. Nucl. Fusion 57, 072006.CrossRefGoogle Scholar
Kraichnan, R. H. 1968 Small-scale structure of a scalar field convected by turbulence. Phys. Fluids 11, 945.Google Scholar
Kraichnan, R. H. 1974 Convection of a passive scalar by a quasi-uniform random straining field. J. Fluid Mech. 64, 737.Google Scholar
Kraichnan, R. H. 1994 Anomalous scaling of a randomly advected passive scalar. Phys. Rev. Lett. 72, 1016.CrossRefGoogle ScholarPubMed
Krommes, J. A. 1997 The clump lifetime revisited: exact calculation of the second-order structure function for a model of forced, dissipative turbulence. Phys. Plasmas 4, 655.Google Scholar
Krommes, J. A. 2015 A tutorial introduction to the statistical theory of turbulent plasmas, a half-century after Kadomtsev’s plasma turbulence and the resonance-broadening theory of Dupree and Weinstock. J. Plasma Phys. 81, 205810601.CrossRefGoogle Scholar
Landau, L. 1946 On the vibration of the electronic plasma. Zh. Eksp. Teor. Fiz. 16, 574.Google Scholar
Laval, G., Pesme, D. & Adam, J.-C. 2016 Wave-particle and wave–wave interactions in hot plasmas: a French historical point of view. Eur. Phys. J. H. doi:10.1140/epjh/e2016-70050-2.Google Scholar
Lenard, A. & Bernstein, I. B. 1958 Plasma oscillations with diffusion in velocity space. Phys. Rev. 112, 1456.Google Scholar
Lesur, M., Diamond, P. H. & Kosuga, Y. 2014a Nonlinear current-driven ion-acoustic instability driven by phase-space structures. Plasma Phys. Control. Fusion 56, 075005.Google Scholar
Lesur, M., Diamond, P. H. & Kosuga, Y. 2014b Phase-space jets drive transport and anomalous resistivity. Phys. Plasmas 21, 112307.Google Scholar
Malmberg, J. H., Wharton, C. B., Gould, R. W. & O’Neil, T. M. 1968 Plasma wave echo experiment. Phys. Rev. Lett. 20, 95.Google Scholar
Mandell, N. R., Dorland, W. & Landreman, M. 2017 Laguerre-Hermite pseudo-spectral velocity formulation of gyrokinetics. J. Plasma Phys. (in press) arXiv:1708.04029.Google Scholar
Manheimer, W. M. 1971 Strong turbulence theory of nonlinear stabilization and harmonic generation. Phys. Fluids 14, 579.Google Scholar
Manheimer, W. M. & Dupree, T. H. 1968 Weak turbulence theory of velocity space diffusion and the nonlinear Landau damping of waves. Phys. Fluids 11, 2709.Google Scholar
Mattor, N. 1992 Can Landau-fluid models describe nonlinear Landau damping? Phys. Fluids B 4, 3952.Google Scholar
Mazitov, R. K. 1965 Damping of plasma waves. J. Appl. Mech. Tech. Phys. 6, 22.Google Scholar
Musher, S. L., Rubenchik, A. M. & Zakharov, V. E. 1995 Weak Langmuir turbulence. Phys. Rep. 252, 177.Google Scholar
Novikov, E. A. 1965 Functionals and the random-force method in turbulence theory. Sov. Phys. JETP 20, 1290.Google Scholar
O’Neil, T. 1965 Collisionless damping of nonlinear plasma oscillations. Phys. Fluids 8, 2255.CrossRefGoogle Scholar
O’Neil, T. M., Winfrey, J. H. & Malmberg, J. H. 1971 Nonlinear interaction of a small cold beam and a plasma. Phys. Fluids 14, 1204.CrossRefGoogle Scholar
Orszag, S. A. & Kraichnan, R. H. 1967 Model equations for strong turbulence in a Vlasov plasma. Phys. Fluids 10, 1720.Google Scholar
Parker, J. T. & Dellar, P. J. 2015 Fourier–Hermite spectral representation for the Vlasov–Poisson system in the weakly collisional limit. J. Plasma Phys. 81, 305810203.Google Scholar
Parker, J. T., Highcock, E. G., Schekochihin, A. A. & Dellar, P. J. 2016 Suppression of phase mixing in drift-kinetic plasma turbulence. Phys. Plasmas 23, 070703.Google Scholar
Passot, T. & Sulem, P. L. 2004 A Landau fluid model for dispersive magnetohydrodynamics. Phys. Plasmas 11, 5173.Google Scholar
Passot, T., Sulem, P. L. & Tassi, E. 2017 Electron-scale reduced fluid models with gyroviscous effects. J. Plasma Phys. 83, 715830402.Google Scholar
Plunk, G. G., Cowley, S. C., Schekochihin, A. A. & Tatsuno, T. 2010 Two-dimensional gyrokinetic turbulence. J. Fluid Mech. 664, 407.CrossRefGoogle Scholar
Plunk, G. G. & Tatsuno, T. 2011 Energy transfer and dual cascade in kinetic magnetized plasma turbulence. Phys. Rev. Lett. 106, 165003.Google Scholar
Robinson, P. A. 1997 Nonlinear wave collapse and strong turbulence. Rev. Mod. Phys. 69, 507.Google Scholar
Rudakov, L. I. & Tsytovich, V. N. 1978 Strong Langmuir turbulence. Phys. Rep. 40, 1.Google Scholar
Schekochihin, A. A.2017 Lecture Notes on Kinetic Theory and Magnetohydrodynamics of Plasmas. http://www-thphys.physics.ox.ac.uk/people/AlexanderSchekochihin/KT/2015/KTLectureNotes.pdf.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Plunk, G. G., Quataert, E. & Tatsuno, T. 2008 Gyrokinetic turbulence: a nonlinear route to dissipation through phase space. Plasma Phys. Control. Fusion 50, 124024.Google Scholar
Schekochihin, A. A., Cowley, S. C., Dorland, W., Hammett, G. W., Howes, G. G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182, 310.Google Scholar
Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L. & McWilliams, J. C. 2004a Simulations of the small-scale turbulent dynamo. Astrophys. J. 612, 276.Google Scholar
Schekochihin, A. A., Haynes, P. H. & Cowley, S. C. 2004b Diffusion of passive scalar in a finite-scale random flow. Phys. Rev. E 70, 046304.Google Scholar
Schekochihin, A. A., Iskakov, A. B., Cowley, S. C., McWilliams, J. C., Proctor, M. R. E. & Yousef, T. A. 2007 Fluctuation dynamo and turbulent induction at low magnetic Prandtl numbers. New J. Phys. 9, 300.Google Scholar
Schekochihin, A. A., Parker, J. T., Highcock, E. G., Dellar, P. J., Dorland, W. & Hammett, G. W. 2016 Phase mixing versus nonlinear advection in drift-kinetic plasma turbulence. J. Plasma Phys. 82, 905820212.Google Scholar
Servidio, S., Chasapis, A., Matthaeus, W. H., Perrone, D., Valentini, F., Parashar, T. N., Veltri, P., Gershman, D., Russell, C. T., Giles, B. et al. 2017 Magnetospheric multiscale (MMS) observation of plasma velocity-space cascade: Hermite representation and theory. Phys. Rev. Lett. 119, 205101.Google Scholar
Smith, S. A.1997 Dissipative closures for statistical moments, fluid moments, and subgrid scales in plasma turbulence. PhD thesis, Princeton University; http://w3.pppl.gov/hammett/sasmith/thesis.html.Google Scholar
Snyder, P. B., Hammett, G. W. & Dorland, W. 1997 Landau fluid models of collisionless magnetohydrodynamics. Phys. Plasmas 4, 3974.CrossRefGoogle Scholar
Sturrock, P. A. 1966 Stochastic acceleration. Phys. Rev. 141, 186.Google Scholar
Sutton, W. G. L. 1943 On the equation of diffusion in a turbulent medium. Proc. R. Soc. Lond. A 182, 48.Google Scholar
Tassi, E., Sulem, P. L. & Passot, T. 2016 Reduced models accounting for parallel magnetic perturbations: gyrofluid and finite Larmor radius-Landau fluid approaches. J. Plasma Phys. 82, 705820601.CrossRefGoogle Scholar
Tatsuno, T., Dorland, W., Schekochihin, A. A., Plunk, G. G., Barnes, M., Cowley, S. C. & Howes, G. G. 2009 Nonlinear phase mixing and phase-space cascade of entropy in gyrokinetic plasma turbulence. Phys. Rev. Lett. 103, 015003.Google Scholar
Teaca, B., Bañón Navarro, A., Jenko, F., Brunner, S. & Villard, L. 2012 Locality and universality in gyrokinetic turbulence. Phys. Rev. Lett. 109, 235003.Google Scholar
Teaca, B., Banón Navarro, A., Told, D. & Jenko, F.2016 Kinetic intermittency in magnetized plasma turbulence. E-print arXiv:1607.03421.Google Scholar
Thornhill, S. G. & ter Haar, D. 1978 Langmuir turbulence and modulational instability. Phys. Rep. 43, 43.Google Scholar
Tsytovich, V. N. 1995 Lectures on Non-linear Plasma Kinetics. Springer.Google Scholar
Vedenov, A. A., Velikhov, E. P. & Sagdeev, R. Z. 1962 Quasilinear theory of plasma oscillations., Nucl. Fusion Suppl. Part 2 465.Google Scholar
Watanabe, T.-H. & Sugama, H. 2004 Kinetic simulation of steady states of ion temperature gradient driven turbulence with weak collisionality. Phys. Plasmas 11, 1476.Google Scholar
Weiland, J. 1992 Nonlinear effects in velocity space and drift wave transport in tokamaks. Phys. Fluids B 4, 1388.Google Scholar
Zakharov, V. E. 1972 Collapse of Langmuir waves. Sov. Phys. JETP 35, 908.Google Scholar
Zakharov, V. E., L’vov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I: Wave Turbulence. Springer.Google Scholar
Zakharov, V. E., Musher, S. L. & Rubenchik, A. M. 1985 Hamiltonian approach to the description of non-linear plasma phenomena. Phys. Rep. 129, 285.Google Scholar
Zeldovich, Ya. B., Ruzmaikin, A. A. & Sokoloff, D. D. 1990 The Almighty Chance. World Scientific.Google Scholar
Zocco, A. & Schekochihin, A. A. 2011 Reduced fluid-kinetic equations for low-frequency dynamics, magnetic reconnection, and electron heating in low-beta plasmas. Phys. Plasmas 18, 102309g.CrossRefGoogle Scholar