Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-02T21:05:40.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Radially anisotropic systems with 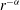$r^{-{\it\alpha}}$ forces: equilibrium states

Part of: Complex Plasma Phenomena

Published online by Cambridge University Press:  13 July 2015

Pierfrancesco Di Cintio ,
L. Ciotti  and
C. Nipoti
Pierfrancesco Di Cintio*
Affiliation:
Dipartimento di Fisica e Astronomia, Università di Firenze e Centro Studi Dinamiche Complesse, via Sansone 1, 50022 Sesto Fiorentino, Italy INFN-Sezione di Firenze, via Sansone 1, 50019 Sesto Fiorentino, Italy
L. Ciotti
Affiliation:
Dipartimento di Fisica e Astronomia, Università di Bologna, viale Berti-Pichat 6/2, 40127 Bologna, Italy
C. Nipoti
Affiliation:
Dipartimento di Fisica e Astronomia, Università di Bologna, viale Berti-Pichat 6/2, 40127 Bologna, Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We continue the study of collisionless systems governed by additive 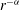$r^{-{\it\alpha}}$ interparticle forces by focusing on the influence of the force exponent ${\it\alpha}$ on radial orbital anisotropy. In this preparatory work, we construct the radially anisotropic Osipkov–Merritt phase-space distribution functions for self-consistent spherical Hernquist models with 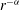$r^{-{\it\alpha}}$ forces and 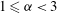$1\leqslant {\it\alpha}<3$ . The resulting systems are isotropic at the centre and increasingly dominated by radial orbits at radii larger than the anisotropy radius 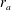$r_{a}$ . For radially anisotropic models we determine the minimum value of the anisotropy radius 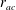$r_{ac}$ as a function of ${\it\alpha}$ for phase-space consistency (such that the phase-space distribution function is nowhere negative for 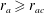$r_{a}\geqslant r_{ac}$ ). We find that 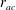$r_{ac}$ decreases for decreasing ${\it\alpha}$ , and that the amount of kinetic energy that can be stored in the radial direction relative to that stored in the tangential directions for marginally consistent models increases for decreasing ${\it\alpha}$ . In particular, we find that isotropic systems are consistent in the explored range of ${\it\alpha}$ . By means of direct 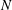$N$ -body simulations, we finally verify that the isotropic systems are also stable.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 5 , October 2015 , 495810504
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

van Albada, T. S. 1982 Dissipationless galaxy formation and the $r^{1/4}$ law. Mon. Not. R. Astron. Soc. 201, 939–955.Google Scholar
An, J. H., van Hese, E. & Baes, M. 2012 Phase-space consistency of stellar dynamical models determined by separable augmented densities. Mon. Not. R. Astron. Soc. 422, 652–664.CrossRefGoogle Scholar
Arfken, G. B. & Weber, N. W. 2005 Mathematical Methods for Physicists, 6th edn. Elsevier.Google Scholar
Barnes, E. I., Lanzel, P. A. & Williams, L. L. R. 2009 Radial orbit instability in collisionless $N$ -body simulations. Astrophys. J. 704, 372–384.Google Scholar
Bekenstein, J. & Milgrom, M. 1984 Does the missing mass problem signal the breakdown of Newtonian gravity? Astrophys. J. 286, 7–14.CrossRefGoogle Scholar
Bertin, G. 2014 Dynamics of Galaxies, 2nd edn. Cambridge University Press.Google Scholar
Bertin, G., Pegoraro, F., Rubini, F. & Vesperini, E. 1994 Linear stability of spherical collisionless stellar systems. Astrophys. J. 434, 94–109.Google Scholar
Bertin, G. & Stiavelli, M. 1989 Stability aspects of a family of anisotropic models of elliptical galaxies. Astrophys. J. 338, 723–734.Google Scholar
Binney, J. & Tremaine, S. 2008 Galactic Dynamics, 2nd edn. Princeton University Press.CrossRefGoogle Scholar
Carollo, C. M., de Zeeuw, P. T. & van der Marel, R. P. 1995 Velocity profiles of Osipkov–Merritt models. Mon. Not. R. Astron. Soc. 276, 1131–1140.CrossRefGoogle Scholar
Chandrasekhar, S. 1995 Newton’s Principia for the Common Reader. Clarendon.CrossRefGoogle Scholar
Chebyshev, P. L. 1853 L’intégration des differentielles irrationelles. J. Math. Pures Appl. 18, 87–111.Google Scholar
Ciotti, L. 1991 Stellar systems following the $R^{1/m}$ luminosity law. Astron. Astrophys. 249, 99–106.Google Scholar
Ciotti, L. 1996 The analytical distribution function of anisotropic two-component Hernquist models. Astrophys. J. 471, 68–81.CrossRefGoogle Scholar
Ciotti, L. 1997 The physical origin of the fundamental plane (of elliptical galaxies). In Proceedings of ESO Workshop on Galaxy Scaling Relations: Origins, Evolution and Applications (ed. Nicolaci da Costa, L. & Renzini, A.), p. 87. Springer.Google Scholar
Ciotti, L. 1999 Modelling elliptical galaxies: phase-space constraints on two-component $({\it\gamma}_{1},{\it\gamma}_{2})$ models. Astrophys. J. 574, 574–591.Google Scholar
Ciotti, L.2000 Lecture Notes on Stellar Dynamics. Scuola Normale Superiore Pisa, Italy, editions Scuola Normale Superiore, Series: Publications of the Scuola Normale Superiore. 160 pp.Google Scholar
Ciotti, L. & Bertin, G. 1999 Analytical properties of the $R^{1/m}$ law. Astron. Astrophys. 352, 447–451.Google Scholar
Ciotti, L. & Binney, J. 2004 Two-body relaxation in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 351, 285–291.Google Scholar
Ciotti, L. & Lanzoni, B. 1997 Stellar systems following the $R^{1/m}$ luminosity law. II. Anisotropy, velocity profiles, and the fundamental plane of elliptical galaxies. Mon. Not. R. Astron. Soc. 321, 724–732.Google Scholar
Ciotti, L. & Morganti, L. 2010a Consistency criteria for generalized Cuddeford systems. Mon. Not. R. Astron. Soc. 401, 1091–1098.Google Scholar
Ciotti, L. & Morganti, L. 2010b How general is the global density slope-anisotropy inequality? Mon. Not. R. Astron. Soc. 408, 1070–1074.Google Scholar
Ciotti, L., Nipoti, C. & Londrillo, P. 2007 Phase mixing in MOND. In Proceedings of the International Workshop on Collective Phenomena in Macroscopic Systems, vol. 177, pp.177–186. World Scientific.Google Scholar
Ciotti, L. & Pellegrini, S. 1992 Self-consistent two-component models of elliptical galaxies. Mon. Not. R. Astron. Soc. 255, 561–571.Google Scholar
Ciotti, L. & Pellegrini, S. 2004 On the use of X-rays to determine dynamical properties of elliptical galaxies. Mon. Not. R. Astron. Soc. 350, 609–614.CrossRefGoogle Scholar
Di Cintio, P.F. & Ciotti, L. 2011 Relaxation of spherical systems with long-range interactions: a numerical investigation. Intl J. Bifurcation Chaos 21, 2279–2283.Google Scholar
Di Cintio, P.F., Ciotti, L. & Nipoti, C. 2013 Relaxation of $N$ -body systems with additive $r^{-{\it\alpha}}$ interparticle forces. Mon. Not. R. Astron. Soc. 431, 3177–3188.Google Scholar
Eddington, A. 1916 The distribution of stars in globular clusters. Mon. Not. R. Astron. Soc. 76, 572–585.Google Scholar
Fridman, A. M. & Polyachenko, V. L. 1984 Physics of Gravitating Systems, 2nd edn. Springer.Google Scholar
Gajda, G., Lokas, E. L. & Wojtak, R. 2015 Radial orbit instability in dwarf dark matter haloes. Mon. Not. R. Astron. Soc. 447, 97–109.Google Scholar
Hernquist, L. 1990 An analytical model for spherical galaxies and bulges. Astrophys. J. 356, 359–364.CrossRefGoogle Scholar
Kuzmin, G. G. & Malasidze, G. D. 1970 On a form of the gravitational potential allowing to solve the problem of plane stellar orbits in elliptic integrals. Tartu Publ. 38, 181–250.Google Scholar
Kuzmin, G. G. & Veltmann, Ü. I. K. 1973 Density projections and generalized isochronic models of spherical stellar systems. Tartu Publ. 40, 281–323.Google Scholar
Londrillo, P., Messina, A. & Stiavelli, M. 1991 Dissipationless galaxy formation revisited. Mon. Not. R. Astron. Soc. 250, 54–68.Google Scholar
Lynden-Bell, D. 1967 Statistical mechanics of violent relaxation. Mon. Not. R. Astron. Soc. 136, 101–121.Google Scholar
Lynden-Bell, D. & Lynden-Bell, R. M. 1982 Relaxation to a perpetually pulsating equilibrium. Proc. R. Soc. Lond. A 455, 475–486.Google Scholar
Merritt, D. 1985 Spherical stellar systems with spheroidal velocity distributions. Astron. J. 90, 1027–1037.Google Scholar
Merritt, D. & Aguilar, L. 1985 A numerical study of the stability of spherical galaxies. Mon. Not. R. Astron. Soc. 217, 787–804.CrossRefGoogle Scholar
Meza, A. & Zamorano, N. 1997 Numerical stability of a family of Osipkov–Merritt models. Astrophys. J. 490, 136–142.Google Scholar
Milgrom, M. 1983 A modification of the Newtonian dynamics as a possible alternative to the hidden mass hypothesis. Astrophys. J. 270, 365–370.Google Scholar
Nipoti, C., Ciotti, L., Binney, J. & Londrillo, P. 2008 Dynamical friction in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 386, 2194–2198.Google Scholar
Nipoti, C., Ciotti, L. & Londrillo, P. 2011 Radial-orbit instability in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 414, 3298–3306.CrossRefGoogle Scholar
Nipoti, C., Londrillo, P. & Ciotti, L. 2002 Radial orbital anisotropy and the fundamental plane of elliptical galaxies. Mon. Not. R. Astron. Soc. 332, 901–914.CrossRefGoogle Scholar
Nipoti, C., Londrillo, P. & Ciotti, L. 2006 Dissipationless collapse, weak homology and central cores of elliptical galaxies. Mon. Not. R. Astron. Soc. 370, 681–690.Google Scholar
Nipoti, C., Londrillo, P. & Ciotti, L. 2007a Dissipationless collapses in modified Newtonian dynamics. Astrophys. J. 660, 256–266.Google Scholar
Nipoti, C., Londrillo, P. & Ciotti, L. 2007b Galaxy merging in modified Newtonian dynamics. Mon. Not. R. Astron. Soc. 381, L104–L108.CrossRefGoogle Scholar
Osipkov, L. P. 1978 General expression for the potential of spherical star systems. Astrophysics 14, 127–135.CrossRefGoogle Scholar
Osipkov, L. P. 1979 Spherical systems of gravitating bodies with an ellipsoidal velocity distribution. Sov. Astron. Lett. 5, 42–44.Google Scholar
Palmer, P. L. & Papaloizou, J. 1987 Instability in spherical stellar systems. Mon. Not. R. Astron. Soc. 224, 1043–1053.Google Scholar
Polyachenko, V. L. 1992 Theory and applications of radial orbit instability in collisionless gravitational systems. Zh. Eksp. Teor. Fiz. 74, 755–763.Google Scholar
Polyachenko, V. L. & Shukhman, I. G. 1981 General models of collisionless spherically symmetric stellar systems – a stability analysis. Sov. Astron. 25, 533–540.Google Scholar
Polyachenko, E. V. & Shukhman, I. G.2015 On the nature of the radial orbit instability in spherically symmetric collisionless stellar systems. Mon. Not. R. Astron. Soc. (in press). arXiv:1504.03513.Google Scholar
Saha, P. 1991 Unstable modes of a spherical stellar system. Mon. Not. R. Astron. Soc. 248, 494–502.Google Scholar
Sérsic, J. L.1968 Atlas de Galaxias Australes. Observatorio Astronomico Cordoba, Cordoba, Argentina.Google Scholar
Srinivasan, K., Mahawar, H. & Sarin, V.2005 A Multipole Based Treecode Using Spherical Harmonics for Potentials of the Form r −𝜆 ICCS. In Computational Science – ICCS 2005, 5th International Conference, Atlanta, GA, USA, May 22–25, 2005, Proceedings, Part I (ed. V. S. Sunderam et al.), Lecture notes in Computational Sciences Series, vol. 3514, pp. 107–114. Springer.CrossRefGoogle Scholar
Stein, E. M. 1970 Singular Integrals and Differentiability Properties of Functions. Princeton University Press.Google Scholar
Sylos-Labini, F., Benhaiem, D. & Joyce, M. 2015 On the generation of triaxiality in the collapse of cold spherical self-gravitating systems. Mon. Not. R. Astron. Soc. 449 (4), 4458–4464.Google Scholar
Trenti, M., Bertin, G. & van Albada, T. S. 2005 A family of models of partially relaxed stellar systems. II. Comparison with the products of collisionless collapse. Astron. Astrophys. 433, 57–72.Google Scholar