Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-12-02T21:57:11.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Proton imaging of stochastic magnetic fields

Published online by Cambridge University Press:  19 December 2017

A. F. A. Bott Open the ORCID record for A. F. A. Bott [Opens in a new window] ,
C. Graziani ,
P. Tzeferacos ,
T. G. White ,
D. Q. Lamb ,
G. Gregori  and
A. A. Schekochihin
A. F. A. Bott*
Affiliation:
Department of Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK
C. Graziani
Affiliation:
FLASH Center for Computational Science, University of Chicago, 5640 S. Ellis Ave, Chicago, IL 60637, USA
P. Tzeferacos
Affiliation:
Department of Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK FLASH Center for Computational Science, University of Chicago, 5640 S. Ellis Ave, Chicago, IL 60637, USA
T. G. White
Affiliation:
Department of Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK Department of Physics, University of Nevada, Reno, NV 89557, USA
D. Q. Lamb
Affiliation:
FLASH Center for Computational Science, University of Chicago, 5640 S. Ellis Ave, Chicago, IL 60637, USA
G. Gregori
Affiliation:
Department of Physics, University of Oxford, Parks Road, Oxford OX1 3PU, UK
A. A. Schekochihin
Affiliation:
Merton College, Merton Street, Oxford OX1 4JD, UK Rudolf Peierls Centre for Theoretical Physics, University of Oxford, 1 Keble Road, Oxford OX1 3NP, UK
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recent laser-plasma experiments (Fox et al., Phys. Rev. Lett., vol. 111, 2013, 225002; Huntington et al., Nat. Phys., vol. 11(2), 2015, 173–176; Tzeferacos et al., Phys. Plasmas, vol. 24(4), 2017a, 041404; Tzeferacos et al., 2017b, arXiv:1702.03016 [physics.plasm-ph]) report the existence of dynamically significant magnetic fields, whose statistical characterisation is essential for a complete understanding of the physical processes these experiments are attempting to investigate. In this paper, we show how a proton-imaging diagnostic can be used to determine a range of relevant magnetic-field statistics, including the magnetic-energy spectrum. To achieve this goal, we explore the properties of an analytic relation between a stochastic magnetic field and the image-flux distribution created upon imaging that field. This ‘Kugland image-flux relation’ was previously derived (Kugland et al., Rev. Sci. Instrum. vol. 83(10), 2012, 101301) under simplifying assumptions typically valid in actual proton-imaging set-ups. 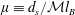We conclude that, as with regular electromagnetic fields, features of the beam’s final image-flux distribution often display a universal character determined by a single, field-scale dependent parameter – the contrast parameter $\unicode[STIX]{x1D707}\equiv d_{s}/{\mathcal{M}}l_{B}$ – which quantifies the relative size of the correlation length 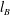$l_{B}$ of the stochastic field, proton displacements 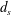$d_{s}$ due to magnetic deflections and the image magnification 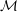${\mathcal{M}}$. For stochastic magnetic fields, we establish the existence of four contrast regimes, under which proton-flux images relate to their parent fields in a qualitatively distinct manner. These are linear, nonlinear injective, caustic and diffusive. The diffusive regime is newly identified and characterised. The nonlinear injective regime is distinguished from the caustic regime in manifesting nonlinear behaviour, but as in the linear regime, the path-integrated magnetic field experienced by the beam can be extracted uniquely. Thus, in the linear and nonlinear injective regimes we show that the magnetic-energy spectrum can be obtained under a further statistical assumption of isotropy. This is not the case in the caustic or diffusive regimes. We discuss complications to the contrast-regime characterisation arising for inhomogeneous, multi-scale stochastic fields, which can encompass many contrast regimes, as well as limitations currently placed by experimental capabilities on one’s ability to extract magnetic-field statistics. The results presented in this paper are of consequence in providing a comprehensive description of proton images of stochastic magnetic fields, with applications for improved analysis of proton-flux images.

Keywords

plasma diagnostics
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 6 , December 2017 , 905830614
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. 1981 The Geometry of Random Fields. Society for Industrial and Applied Mathematics (SIAM).Google Scholar
Arévalo, P., Churazov, E., Zhuravleva, I., Hernández-Monteagudo, C. & Revnivtsev, M. 2012 A Mexican hat with holes: calculating low-resolution power spectra from data with gaps. Mon. Not. R. Astron. Soc. 426 (3), 1793–1807.CrossRefGoogle Scholar
Berry, M. V. & Upstill, C. 1980 Catastrophe optics: morphologies of caustics and their diffraction patterns. Prog. Optics. 18, 257–346.CrossRefGoogle Scholar
Birdsall, C. K. & Langdon, A. B. 1991 Plasma Physics via Computer Simulation. Institute of Physics Publishing.CrossRefGoogle Scholar
Blandford, R. & Eichler, D. 1987 Particle acceleration at astrophysical shocks: a theory of cosmic ray origin. Phys. Rep. 154 (1), 1–75.CrossRefGoogle Scholar
Borghesi, M., Campbell, D. H., Schiavi, A., Haines, M. G., Willi, O., MacKinnon, A. J., Patel, P., Gizzi, L. A., Galimberti, M., Clarke, R. J. et al. 2002 Electric field detection in laser-plasma interaction experiments via the proton imaging technique. Phys. Plasmas 9 (5), 2214–2220.Google Scholar
Borghesi, M., Fuchs, J., Bulanov, S., MacKinnon, A., Patel, P. & Roth, M. 2006 Fast ion generation by high-intensity laser irradiation of solid targets and applications. Fusion Sci. Technol. 49 (3), 412–439.CrossRefGoogle Scholar
Borghesi, M., Kar, S., Romagnani, L., Toncian, T., Antici, P., Audebert, P., Brambrink, E., Ceccherini, F., Cecchetti, C. A., Fuchs, J. et al. 2007 Impulsive electric fields driven by high-intensity laser matter interactions. Laser Part. Beams 25 (1), 161–167.CrossRefGoogle Scholar
Brenier, Y. 1991 Polar factorization and monotone rearrangement of vector-valued functions. Commun. Pure Appl. Maths 44 (4), 375–417.Google Scholar
Churazov, E., Vikhlinin, A., Zhuravleva, I., Schekochihin, A., Parrish, I., Sunyaev, R., Forman, W., Böhringer, H. & Randall, S. 2012 X-ray surface brightness and gas density fluctuations in the coma cluster. Mon. Not. R. Astron. Soc. 421 (2), 1123–1135.CrossRefGoogle Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dean, E. J. & Glowinski, R. 2006 Numerical methods for fully nonlinear elliptic equations of the Monge–Ampère type. Comput. Meth. Appl. Mech. Engng. 195 (13), 1344–1386.Google Scholar
Dolginov, A. Z. & Toptygin, I. 1967 Multiple scattering of particles in a magnetic field with random inhomogeneities. Sov. Phys. JETP 24, 1195.Google Scholar
Ensslin, T. & Vogt, C. 2003 The magnetic power spectrum in Faraday rotation screens. Astron. Astrophys. 401 (3), 835–848.Google Scholar
Fox, W., Fiksel, G., Bhattacharjee, A., Chang, P.-Y., Germaschewski, K., Hu, S. X. & Nilson, P. M. 2013 Filamentation instability of counterstreaming laser-driven plasmas. Phys. Rev. Lett. 111, 225002.CrossRefGoogle ScholarPubMed
Gangbo, W. & McCann, R. J. 1996 The geometry of optimal transportation. Acta Math. 177 (2), 113–161.CrossRefGoogle Scholar
Golitsyn, G. S. 1960 Fluctuations of the magnetic field and current density in a turbulent flow of a weakly conducting fluid. Sov. Phys. Dokl. 5, 536.Google Scholar
Graziani, C., Tzeferacos, P., Lamb, D. Q. & Li, C.2016 Inferring morphology and strength of magnetic fields from proton radiographs. arXiv:1603.08617 [physics.plasm-ph].CrossRefGoogle Scholar
Gregori, G., Reville, B. & Miniati, F. 2015 The generation and amplification of intergalactic magnetic fields in analogue laboratory experiments with high power lasers. Phys. Rep. 601, 1–34.Google Scholar
Hall, D. E. & Sturrock, P. A. 1967 Diffusion, scattering, and acceleration of particles by stochastic electromagnetic fields. Phys. Fluids 10 (12), 2620–2628.CrossRefGoogle Scholar
Huntington, C. M., Fiuza, F., Ross, J. S., Zylstra, A. B., Drake, R. P., Froula, D. H., Gregori, G., Kugland, N. L., Kuranz, C. C., Levy, M. C. et al. 2015 Observation of magnetic field generation via the Weibel instability in interpenetrating plasma flows. Nat. Phys. 11 (2), 173–176.CrossRefGoogle Scholar
Jokipii, J. R. 1972 Fokker–Planck equations for charged-particle transport in random fields. Astrophys. J. 172, 319.CrossRefGoogle Scholar
Kasim, M. F., Ceurvorst, L., Ratan, N., Sadler, J., Chen, N., Sävert, A., Trines, R., Bingham, R., Burrows, P. N., Kaluza, M. C. et al. 2017 Quantitative shadowgraphy and proton radiography for large intensity modulations. Phys. Rev. E 95, 023306.Google ScholarPubMed
Krall, N. A. & Trivelpiece, A. W. 1973 Principles of Plasma Physics. McGraw-Hill.CrossRefGoogle Scholar
Kugland, N. L., Ryutov, D. D., Plechaty, C., Ross, J. S. & Park, H.-S. 2012 Invited article: relation between electric and magnetic field structures and their proton-beam images. Rev. Sci. Instrum. 83 (10), 101301.Google Scholar
Levy, M. C., Ryutov, D. D., Wilks, S. C., Ross, J. S., Huntington, C. M., Fiuza, F., Martinez, D. A., Kugland, N. L., Baring, M. G. & Park, H.-S. 2015 Development of an interpretive simulation tool for the proton radiography technique. Rev. Sci. Instrum. 86 (3), 033302.CrossRefGoogle ScholarPubMed
Li, C. K., Séguin, F. H., Frenje, J. A., Rygg, J. R., Petrasso, R. D., Town, R. P. J., Amendt, P. A., Hatchett, S. P., Landen, O. L., MacKinnon, A. J. et al. 2006 Measuring E and B fields in laser-produced plasmas with monoenergetic proton radiography. Phys. Rev. Lett. 97, 135003.Google Scholar
Lucy, L. B. 1974 An iterative technique for the rectification of observed distributions. Astron. J. 79, 745.CrossRefGoogle Scholar
MacKinnon, A. J., Patel, P. K., Borghesi, M., Clarke, R. C., Freeman, R. R., Habara, H., Hatchett, S. P., Hey, D., Hicks, D. G., Kar, S. et al. 2006 Proton radiography of a laser-driven implosion. Phys. Rev. Lett. 97, 045001.Google Scholar
MacKinnon, A. J., Patel, P. K., Town, R. P., Edwards, M. J., Phillips, T., Lerner, S. C., Price, D. W., Hicks, D., Key, M. H., Hatchett, S. et al. 2004 Proton radiography as an electromagnetic field and density perturbation diagnostic (invited). Rev. Sci. Instrum. 75 (10), 3531–3536.CrossRefGoogle Scholar
Manuel, M. J. E., Zylstra, A. B., Rinderknecht, H. G., Casey, D. T., Rosenberg, M. J., Sinenian, N., Li, C. K., Frenje, J. A., Séguin, F. H. & Petrasso, R. D. 2012 Source characterization and modeling development for monoenergetic-proton radiography experiments on OMEGA. Rev. Sci. Instrum. 83 (6), 063506.CrossRefGoogle ScholarPubMed
Moffatt, K. 1961 The amplification of a weak applied magnetic field by turbulence in fluids of moderate conductivity. J. Fluid Mech. 11 (4), 625–635.CrossRefGoogle Scholar
Mondal, S., Narayanan, V., Ding, W. J., Lad, A. D., Hao, B., Ahmad, S., Wang, W. M., Sheng, Z. M., Sengupta, S., Kaw, P. et al. 2012 Direct observation of turbulent magnetic fields in hot, dense laser produced plasmas. Proc. Natl Acad. Sci. USA 109 (21), 8011–8015.CrossRefGoogle ScholarPubMed
Nürnberg, F., Schollmeier, M., Brambrink, E., Blažević, A., Carroll, D. C., Flippo, K., Gautier, D. C., Geißel, M., Harres, K., Hegelich, B. M. et al. 2009 Radiochromic film imaging spectroscopy of laser-accelerated proton beams. Rev. Sci. Instrum. 80 (3), 033301.Google Scholar
Parker, E. N. 1965 The passage of energetic charged particles through interplanetary space. Planet. Space Sci. 13 (1), 9–49.Google Scholar
Richardson, W. H. 1972 Bayesian-based iterative method of image restoration. J. Opt. Soc. Am. 62 (1), 55–59.CrossRefGoogle Scholar
Romagnani, L., Borghesi, M., Cecchetti, C. A., Kar, S., Antici, P., Audebert, P., Bandhoupadjay, S., Ceccherini, F., Cowan, T., Fuchs, J. et al. 2008 Proton probing measurement of electric and magnetic fields generated by ns and ps laser-matter interactions. Laser Part. Beams 26 (2), 241–248.Google Scholar
Romagnani, L., Fuchs, J., Borghesi, M., Antici, P., Audebert, P., Ceccherini, F., Cowan, T., Grismayer, T., Kar, S., Macchi, A. et al. 2005 Dynamics of electric fields driving the laser acceleration of multi-MeV protons. Phys. Rev. Lett. 95, 195001.CrossRefGoogle ScholarPubMed
Sarri, G., Macchi, A., Cecchetti, C. A., Kar, S., Liseykina, T. V., Yang, X. H., Dieckmann, M. E., Fuchs, J., Galimberti, M., Gizzi, L. A. et al. 2012 Dynamics of self-generated, large amplitude magnetic fields following high-intensity laser matter interaction. Phys. Rev. Lett. 109, 205002.Google Scholar
Schekochihin, A. A., Cowley, S. C., Taylor, S. F., Maron, J. L. & McWilliams, J. C. 2004 Simulations of the small-scale turbulent dynamo. Astrophys. J. 612 (1), 276.Google Scholar
Schekochihin, A. A., Iskakov, A. B., Cowley, S. C., McWilliams, J. C., Proctor, M. R. E. & Yousef, T. A. 2007 Fluctuation dynamo and turbulent induction at low magnetic Prandtl numbers. New J. Phys. 9 (8), 300.Google Scholar
Séguin, F. H., DeCiantis, J. L., Frenje, J. A., Kurebayashi, S., Li, C. K., Rygg, J. R., Chen, C., Berube, V., Schwartz, B. E., Petrasso, R. D. et al. 2004 D3He-proton emission imaging for inertial-confinement-fusion experiments (invited). Rev. Sci. Instrum. 75 (10), 3520–3525.Google Scholar
Shinozuka, M. & Deodatis, G. 1996 Simulation of multi-dimensional Gaussian stochastic fields by spectral representation. Appl. Mech. Rev. 49 (1), 29–53.Google Scholar
Sulman, M. M., Williams, J. F. & Russell, R. D. 2011 An efficient approach for the numerical solution of the Monge–Ampère equation. Appl. Numer. Maths 61 (3), 298–307.Google Scholar
Tzeferacos, P., Rigby, A., Bott, A., Bell, A. R., Bingham, R., Casner, A., Cattaneo, F., Churazov, E. M., Emig, J., Fiuza, F. et al. 2017a Numerical modeling of laser-driven experiments aiming to demonstrate magnetic field amplification via turbulent dynamo. Phys. Plasmas 24 (4), 041404.Google Scholar
Tzeferacos, P., Rigby, A., Bott, A., Bell, A. R., Bingham, R., Casner, A., Cattaneo, F., Churazov, E. M., Emig, J., Fiuza, F. et al. 2017b Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma. arXiv:1702.03016 [physics.plasm-ph].Google Scholar
Villani, C. 2008 Optimal Transport: Old and New, vol. 338. Springer.Google Scholar
Welch, D. R., Rose, D. V., Clark, R. E., Genoni, T. C. & Hughes, T. P. 2004 Implementation of an non-iterative implicit electromagnetic field solver for dense plasma simulation. Comput. Phys. Commun. 164 (1), 183–188.Google Scholar
Wilks, S. C., Langdon, A. B., Cowan, T. E., Roth, M., Singh, M., Hatchett, S., Key, M. H., Pennington, D., MacKinnon, A. & Snavely, R. A. 2001 Energetic proton generation in ultra-intense laser–solid interactions. Phys. Plasmas 8 (2), 542–549.Google Scholar
Yamazaki, F. & Shinozuka, M. 1988 Digital generation of non-Gaussian stochastic fields. J. Engng Mech. ASCE 114 (7), 1183–1197.CrossRefGoogle Scholar
Ziegler, J. F. 1999 Stopping of energetic light ions in elemental matter. J. Appl. Phys./Rev. Appl. Phys. 85 (3), 1249–1272.Google Scholar