Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-23T22:23:33.594Z Has data issue: false hasContentIssue false
  • English
  • Français

Parallel 3-D particle-in-cell modelling of charged ultrarelativistic beam dynamics

Part of: Complex Plasma Phenomena

Published online by Cambridge University Press:  05 November 2015

Marina A. Boronina  and
Vitaly A. Vshivkov
Marina A. Boronina*
Affiliation:
Institute of Computational Mathematics and Mathematical Geophysics of Siberian Branch of Russian Academy of Sciences, Novosibirsk, Russia
Vitaly A. Vshivkov
Affiliation:
Institute of Computational Mathematics and Mathematical Geophysics of Siberian Branch of Russian Academy of Sciences, Novosibirsk, Russia
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a three-dimensional (3-D) particle-in-cell (PIC) model and parallel code for the self-consistent motion of charged ultrarelativistic beams ( 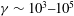${\it\gamma}\sim 10^{3}{-}10^{5}$ ) in supercolliders. We use the 3-D set of Maxwell’s equations for the electromagnetic fields, and the Vlasov equation for the distribution function of the beam particles. The model incorporates automatically the longitudinal effects, which can play a significant role in the cases of super-high densities. We present numerical results for the dynamics of two focused ultrarelativistic beams with a size ratio 10:1:100. The results demonstrate high efficiency of the proposed computational methods and algorithms, which are applicable to a variety of problems in relativistic plasma physics.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 6 , December 2015 , 495810605
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, E. B.1998 Odysseus: a dynamic strong–strong beam–beam simulation for storage rings. PhD thesis, Cornell University.Google Scholar
Basetti, M. & Erskine, G.1980 Closed expression for the electric field of a two-dimensional gaussian charge, CERNISR-ISR-TH/80-06.Google Scholar
Boronina, M. A. & Korneev, V. D. 2013 The parallel three-dimensional pic code for the numerical modeling of ultrarelativistic beams. Bull. NCC: Numer. Anal. 16, 15–22.Google Scholar
Boronina, M. A., Vshivkov, V. A., Levichev, E. B., Nikitin, S. A. & Snytnikov, V. N. 2007 An algorithm for the three-dimensional modeling of ultrarelativistic beams. Numer. Meth. Prog. 8 (2), 203–210.Google Scholar
Chen, P. & Yokoya, K. 1988 Disruption effects from the interaction of round $e^{+}$ and $e^{-}$ beams. Phys. Rev. D D38 (3), 987–1000.Google Scholar
Hirata, K. 1995 Don’t be afraid of beam–beam interactions with a large crossing angle. Phys. Rev. Lett. 74, 2228–2231.Google Scholar
Hockney, R. W. & Eastwood, J. W. 1981 Computer Simulation Using Particles. McGraw-Hill.Google Scholar
Langdon, A. B. & Lasinski, B. F. 1976 Electromagnetic and relativistic plasma simulation models. Meth. Comput. Phys. 16, 327–366.Google Scholar
Lotov, K. V., Timofeev, I. V., Mesyats, E. A., Snytnikov, A. V. & Vshivkov, V. A. 2015 Note on quantitatively correct simulations of the kinetic beam-plasma instability. Phys. Plasmas 22 (2).Google Scholar
Pivi, M. 2007 Beam–beam Effects in Future Linear Colliders. US Particle Accelerator School.Google Scholar
Qiang, J., Furman, M. A. & Ryne, R. D. 2004 A parallel particle-in-cell model for beam–beam interaction in high energy ring colliders. J. Comput. Phys. 198, 278–294.Google Scholar
Qiang, J. & Li, X. 2010 Particle–field decomposition and domain decomposition in parallel particle-in-cell beam dynamics simulation. Comput. Phys. Commun. 181, 2024–2034.CrossRefGoogle Scholar
Schulte, D.1996 Study of electromagnetic and hadronic background in the interaction region of the tesla collider. PhD thesis, University of Hamburg.Google Scholar
Villasenor, J. & Buneman, O. 1992 Rigorous charge conservation for local electromagnetic field solvers. Comput. Phys. Commun. 69 (2–3), 306–316.Google Scholar
Vshivkov, V. A. & Boronina, M. A. 2012 Three-dimensional simulation of ultrarelativistic charged beams dynamics: study of initial and boundary conditions. Matem. Mod. 24 (2), 67–83.Google Scholar