Published online by Cambridge University Press: 26 November 2018
In contrast to hydrodynamic vortices, vortices in a plasma contain an electric current circulating around the centre of the vortex, which generates a magnetic field localized inside. Using computer simulations, we demonstrate that the magnetic field associated with the vortex gives rise to a mechanism of dissipation of the vortex pair in a collisionless plasma, leading to fast annihilation of the magnetic field with its energy transforming into the energy of fast electrons, secondary vortices and plasma waves. Two major contributors to the energy damping of a double vortex system, namely, magnetic field annihilation and secondary vortex formation, are regulated by the size of the vortex with respect to the electron skin depth, which scales with the electron 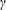 $\unicode[STIX]{x1D6FE}$ factor,
$\unicode[STIX]{x1D6FE}$ factor, 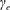 $\unicode[STIX]{x1D6FE}_{e}$, as
$\unicode[STIX]{x1D6FE}_{e}$, as 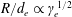 $R/d_{e}\propto \unicode[STIX]{x1D6FE}_{e}^{1/2}$. Magnetic field annihilation appears to be dominant in mildly relativistic vortices, while for the ultrarelativistic case, secondary vortex formation is the main channel for damping of the initial double vortex system.
$R/d_{e}\propto \unicode[STIX]{x1D6FE}_{e}^{1/2}$. Magnetic field annihilation appears to be dominant in mildly relativistic vortices, while for the ultrarelativistic case, secondary vortex formation is the main channel for damping of the initial double vortex system.