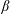1 Introduction
The pedestal region of current fusion devices is both a boon and a serious obstacle to achieving sustained fusion power. Discovered by pioneering work on the ASDEX tokamak in Germany (Wagner et al.
Reference Wagner, Becker, Behringer, Campbell, Eberhagen, Engelhardt, Fussmann, Gehre, Gernhardt and Gierke1982; The ASDEX Team 1989), the ‘
![]() $H$
-mode edge pedestal’ or ‘edge transport barrier’ is a narrow region at the edge of the tokamak where extremely steep gradients can be maintained (thus improving confinement) but which intermittently relaxes through the release of large amounts of hot plasma, known as ‘edge localised modes’(Zohm Reference Zohm1996) (henceforth ELMs). The dichotomy between the confinement that can make a tokamak into a smaller and more efficient reactor and the ELMs that can severely damage that reactor has led to a vast amount of study of pedestals since their discovery.
$H$
-mode edge pedestal’ or ‘edge transport barrier’ is a narrow region at the edge of the tokamak where extremely steep gradients can be maintained (thus improving confinement) but which intermittently relaxes through the release of large amounts of hot plasma, known as ‘edge localised modes’(Zohm Reference Zohm1996) (henceforth ELMs). The dichotomy between the confinement that can make a tokamak into a smaller and more efficient reactor and the ELMs that can severely damage that reactor has led to a vast amount of study of pedestals since their discovery.
Enormous strides have been made, including understanding of the fundamental instabilities that are responsible for ELMs (Connor et al. Reference Connor, Hastie, Wilson and Miller1998; Snyder et al. Reference Snyder, Wilson, Ferron, Lao, Leonard, Osborne, Turnbull, Mossessian, Murakami and Xu2002) and incorporating this knowledge into successful analysis of experiments (Snyder et al. Reference Snyder, Burrell, Wilson, Chu, Fenstermacher, Leonard, Moyer, Osborne, Umansky and West2007, Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). Experimentally, analyses have been made from data acquired on multiple machines (Beurskens et al. Reference Beurskens, Osborne, Schneider, Wolfrum, Frassinetti, Groebner, Lomas, Nunes, Saarelma and Scannell2011), but the narrowness of the pedestal and the difficulty of making these measurements has hampered making predictions for future devices. Indeed, recent results and analyses (Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017; Kotschenreuther et al. Reference Kotschenreuther, Hatch, Mahajan, Valanju, Zheng and Liu2017) suggest that the scaling of the pedestal width with fundamental plasma parameter from current machines to ITER may be in doubt. More detailed modelling is thus essential.
Edge modelling comprises both first principles analysis and a large and established effort in trying to understand existing devices through interpretative modelling. Many difficulties arise in modelling this region of the plasma; any model must be able to handle large, rapidly evolving perturbations associated with ELMs as well as small-scale fluctuations that may regulate the residual transport through the inter-ELM pedestal. In addition, the collisionality of the plasma may vary by orders of magnitude across the pedestal. Taking data from a multi-machine comparison (Militello & Fundamenski Reference Militello and Fundamenski2011), the collisionality at the pedestal top for the joint European torus (JET) is
![]() $\unicode[STIX]{x1D708}_{e}^{\ast }\approx 4\times 10^{-3}$
climbing to
$\unicode[STIX]{x1D708}_{e}^{\ast }\approx 4\times 10^{-3}$
climbing to
![]() $\unicode[STIX]{x1D708}_{e}^{\ast }\approx 0.13$
at the separatrix. Using the predictions for ITER in the same paper, the collisionality at the pedestal top is now
$\unicode[STIX]{x1D708}_{e}^{\ast }\approx 0.13$
at the separatrix. Using the predictions for ITER in the same paper, the collisionality at the pedestal top is now
![]() $\unicode[STIX]{x1D708}_{e}^{\ast }\approx 4\times 10^{-4}$
and still
$\unicode[STIX]{x1D708}_{e}^{\ast }\approx 4\times 10^{-4}$
and still
![]() $\unicode[STIX]{x1D708}_{e}^{\ast }\sim 0.2$
at the separatrix. This indicates a trend towards increasingly collisionless pedestals as machines get larger, driven in part by divertor heat load requirements preventing a high separatrix temperature. Suitable modelling must therefore be able to transition from collisionless to collisional physics across the pedestal region.
$\unicode[STIX]{x1D708}_{e}^{\ast }\sim 0.2$
at the separatrix. This indicates a trend towards increasingly collisionless pedestals as machines get larger, driven in part by divertor heat load requirements preventing a high separatrix temperature. Suitable modelling must therefore be able to transition from collisionless to collisional physics across the pedestal region.
Several main branches of research into near-edge (i.e. regions at the edge of the plasma, but still inside the closed-field-line region) modelling currently exist. The most experimentally successful approach has been that taken by the EPED collaboration (Snyder et al.
Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011, Reference Snyder, Burrell, Wilson, Chu, Fenstermacher, Leonard, Moyer, Osborne, Umansky and West2007). This consists of linear magnetohydrodynamic (MHD) modelling (with the ELITE code) of the peeling-ballooning mode to determine the onset of an ELM, the use of the infinite-
![]() $n$
ballooning stability criterion as a proxy for the stability of the inter-ELM pedestal to microturbulence and an assumption that the pedestal is pinned to this stability threshold between ELMs. Despite the success of this model, the ad hoc marginal stability criterion is required to constrain the width of pedestals, the linear stability calculation may neglect important kinetic effects and the model has no capacity for handling time-dependent inter-ELM dynamics. The dominant paradigm for first-principles edge modelling is that of ‘drift reduced’ or other anisotropic fluid equations (Zeiler, Drake & Rogers Reference Zeiler, Drake and Rogers1997). These are the basis of many current simulation codes, such as GBS (Ricci et al.
Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012), and also older two-dimensional codes including SOLPS and others (Schneider et al.
Reference Schneider, Bonnin, Borrass, Coster, Kastelewicz, Reiter, Rozhansky and Braams2006), and have been used to study the pedestal directly (Nielsen Reference Rasmussen, Nielsen, Madsen, Naulin and Xu2016). Gyrofluid equations, originally developed for the core (Hammett et al.
Reference Hammett, Beer, Dorland, Cowley and Smith1993) have also found much use in edge modelling (Scott Reference Scott1997, Reference Scott2007). Gyrofluid models are derived by taking moments of gyrokinetic equations and then applying one of a variety of closure conditions. These models have the advantage that a limited number of fluid moments is numerically tractable even in complex edge geometries. However, the strong requirements on collisionality for Braginskii equations to be applicable are often not satisfied in high-performance pedestals. Gyrofluid equations at low collisionality become increasingly plagued by questions of the validity of the chosen closure scheme, and lack a first-principles justification for the closures used. Thus, to handle a potentially trans-collisional pedestal region, we will take a kinetic approach.
$n$
ballooning stability criterion as a proxy for the stability of the inter-ELM pedestal to microturbulence and an assumption that the pedestal is pinned to this stability threshold between ELMs. Despite the success of this model, the ad hoc marginal stability criterion is required to constrain the width of pedestals, the linear stability calculation may neglect important kinetic effects and the model has no capacity for handling time-dependent inter-ELM dynamics. The dominant paradigm for first-principles edge modelling is that of ‘drift reduced’ or other anisotropic fluid equations (Zeiler, Drake & Rogers Reference Zeiler, Drake and Rogers1997). These are the basis of many current simulation codes, such as GBS (Ricci et al.
Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012), and also older two-dimensional codes including SOLPS and others (Schneider et al.
Reference Schneider, Bonnin, Borrass, Coster, Kastelewicz, Reiter, Rozhansky and Braams2006), and have been used to study the pedestal directly (Nielsen Reference Rasmussen, Nielsen, Madsen, Naulin and Xu2016). Gyrofluid equations, originally developed for the core (Hammett et al.
Reference Hammett, Beer, Dorland, Cowley and Smith1993) have also found much use in edge modelling (Scott Reference Scott1997, Reference Scott2007). Gyrofluid models are derived by taking moments of gyrokinetic equations and then applying one of a variety of closure conditions. These models have the advantage that a limited number of fluid moments is numerically tractable even in complex edge geometries. However, the strong requirements on collisionality for Braginskii equations to be applicable are often not satisfied in high-performance pedestals. Gyrofluid equations at low collisionality become increasingly plagued by questions of the validity of the chosen closure scheme, and lack a first-principles justification for the closures used. Thus, to handle a potentially trans-collisional pedestal region, we will take a kinetic approach.
Recently, kinetic simulations of the plasma edge have been performed. The first category of these are the global gyrokinetic simulations (Ku et al.
Reference Ku, Chang, Adams, Cummings, Hinton, Keyes, Klasky, Lee, Lin and Parker2006; Chang et al.
Reference Chang, Ku, Loarte, Parail, Kchl, Romanelli, Maingi, Ahn, Gray and Hughes2017; Shi et al.
Reference Shi, Hammett, Stoltzfus-Dueck and Hakim2017). These endeavour to capture all the dynamics of the edge region, from the macro scales down to the ion gyroradius scale. The computational expense is titanic, and thus parameter scans, and predictive modelling are currently out of reach for most applications. The second category of kinetic simulations only seeks to tackle turbulence in the edge, and have shed some light upon the inter-ELM pedestal (Dickinson et al.
Reference Dickinson, Roach, Saarelma, Scannell, Kirk and Wilson2012, Reference Dickinson, Roach, Saarelma, Scannell, Kirk and Wilson2013; Hatch et al.
Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017; Kotschenreuther et al.
Reference Kotschenreuther, Hatch, Mahajan, Valanju, Zheng and Liu2017). These simulations have been conducted despite the fact that the levels of
![]() $\boldsymbol{E}\times \boldsymbol{B}$
shear and flow velocities in the pedestal are not consistent with the assumptions under which gyrokinetics is usually derived (Abel et al.
Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). Thus, we seek to embed gyrokinetics within a more complete pedestal model.
$\boldsymbol{E}\times \boldsymbol{B}$
shear and flow velocities in the pedestal are not consistent with the assumptions under which gyrokinetics is usually derived (Abel et al.
Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013). Thus, we seek to embed gyrokinetics within a more complete pedestal model.
Bridging the gap between fluid models that cannot fully capture the kinetic physics, and gyrokinetic modelling that is extremely expensive and hard to interpret, we instead use a first-principles multiscale approach. Our formulation neatly separates the physics of ELMs, coherent oscillations and inter-ELM turbulence. This permits models for each component that are only as complex as needed, rather than a model that endeavours to rigorously include all possible physics. This conceptual simplification should enable more detailed studies of each separate part of the pedestal physics than is currently possible. However, in this paper we only present a new model for the pedestal, which, in this work, we consider to be the steep gradient part of the closed-field-line region – we leave the issues of extending this to an open-field-line region at the top of the scrape-off layer to future work.
The structure of the remainder of the paper, which lays this model out in detail, is as follows. In § 2 we discuss the physics needed to capture ELMs. Our physical requirements are translated into formal ordering assumptions in § 2.1. In § 2.2 we follow the well-trodden paths of asymptotic theory to turn our ordering assumptions into a closed set of equations for ELM dynamics.
Proceeding to the longer, inter-ELM, time scale in § 3 we follow the same procedure, presenting our orderings in § 3.1 and the equations for the inter-ELM evolution in § 3.2. However, in this procedure we have to introduce an explicit multiple-scales approach to handle inter-ELM turbulence – governed in turn by orderings and equations that are detailed in § 3.3.
Finally, in § 4 we make detailed contact between our model and existing models of the pedestal. In § 4.1 we describe how our model can be integrated with existing validated models for the core and scrape-off layer, acting as a boundary condition for both. Then, in § 4.4, we compare our model to the models currently used to study the pedestal. Ultimately, we end the paper with a summary of our results in § 5 and some discussion of exploration of new avenues this model may open up.
2 Fast and furious: the physics of edge localised modes
As alluded to in the introduction, ELMs are the large-amplitude convulsions of the edge pedestal that pose a great threat to current fusion devices. For this reason, ELM stability must be comprehensively addressed in any plausible pedestal model. To this end, in § 2.1 we codify the physics of ELMs in terms of the temporal and spatial scales of interest, and relations between plasma parameters. These are then applied in § 2.2 to obtain the dynamical equations governing ELMs.
2.1 Orderings for ELM dynamics
ELMs are now well understood to be nonlinear peeling-ballooning modes (Connor et al.
Reference Connor, Hastie, Wilson and Miller1998). These modes are driven by the combination of edge current density, curvature and pressure gradients. They naturally occur on an Alfvénic time scale, that is one which is comparable to
![]() $L_{\Vert }/v_{\text{A}}$
, where
$L_{\Vert }/v_{\text{A}}$
, where
![]() $L_{\Vert }$
is the typical length scale of the instability along a field line and
$L_{\Vert }$
is the typical length scale of the instability along a field line and
![]() $v_{\text{A}}$
is the Alfvén velocity. In this work we will use Gaussian units throughout and so, explicitly,
$v_{\text{A}}$
is the Alfvén velocity. In this work we will use Gaussian units throughout and so, explicitly,
![]() $v_{\text{A}}=B/\sqrt{4\unicode[STIX]{x03C0}\sum _{s}m_{s}n_{s}}$
where
$v_{\text{A}}=B/\sqrt{4\unicode[STIX]{x03C0}\sum _{s}m_{s}n_{s}}$
where
![]() $B$
is the magnetic field strength, and the plasma is composed of several species with masses,
$B$
is the magnetic field strength, and the plasma is composed of several species with masses,
![]() $m_{s}$
, and densities,
$m_{s}$
, and densities,
![]() $n_{s}$
. The parallel length scale
$n_{s}$
. The parallel length scale
![]() $L_{\Vert }$
will be taken to be the longest length scale in our system, and is comparable to the connection length of the magnetic field. In general this means that the defining relationship is
$L_{\Vert }$
will be taken to be the longest length scale in our system, and is comparable to the connection length of the magnetic field. In general this means that the defining relationship is
![]() $L_{\Vert }\sim (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B)^{-1}$
, whereas
$L_{\Vert }\sim (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ln B)^{-1}$
, whereas
![]() $L_{\Vert }$
is only ever used in our asymptotic orderings prefactors of order unity do not matter and will be neglected.
$L_{\Vert }$
is only ever used in our asymptotic orderings prefactors of order unity do not matter and will be neglected.
In order to cause such violent instabilities, the pressure gradients must be large, with the pressure varying over a distance
![]() $L_{\bot }\ll L_{\Vert }$
perpendicular to the field lines. Indeed, pedestals are observed to be extremely narrow structures in current experiments (Beurskens et al.
Reference Beurskens, Osborne, Schneider, Wolfrum, Frassinetti, Groebner, Lomas, Nunes, Saarelma and Scannell2011). Hence we adopt
$L_{\bot }\ll L_{\Vert }$
perpendicular to the field lines. Indeed, pedestals are observed to be extremely narrow structures in current experiments (Beurskens et al.
Reference Beurskens, Osborne, Schneider, Wolfrum, Frassinetti, Groebner, Lomas, Nunes, Saarelma and Scannell2011). Hence we adopt
as our fundamental small parameter.
The most basic stability limit for the ballooning part of the peeling-ballooning mode is a limit on
![]() $\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}\sum _{s}n_{s}T_{s}/B^{2}$
, with
$\unicode[STIX]{x1D6FD}=8\unicode[STIX]{x03C0}\sum _{s}n_{s}T_{s}/B^{2}$
, with
![]() $T_{s}$
the temperature of species
$T_{s}$
the temperature of species
![]() $s$
.Footnote
1
This limit derives from the constraint that the energy required to bend field lines must be comparable to the energy released by relaxing the pressure gradient (Freidberg Reference Freidberg2014). Estimating this balance, we obtain
$s$
.Footnote
1
This limit derives from the constraint that the energy required to bend field lines must be comparable to the energy released by relaxing the pressure gradient (Freidberg Reference Freidberg2014). Estimating this balance, we obtain
which immediately implies that
![]() $\unicode[STIX]{x1D6FD}$
must be small in these systems. Note, in our slightly unconventional usage
$\unicode[STIX]{x1D6FD}$
must be small in these systems. Note, in our slightly unconventional usage
![]() $a\sim b$
means that
$a\sim b$
means that
![]() $a$
and
$a$
and
![]() $b$
are of the same asymptotic order as
$b$
are of the same asymptotic order as
![]() $\unicode[STIX]{x1D716}\rightarrow 0$
, but may differ by numerical prefactors of order unity. It is also important at this stage to note that we are expanding in the ratio of the pedestal width to the magnetic scale length, not in the aspect ratio of the magnetic surfaces.Footnote
2
$\unicode[STIX]{x1D716}\rightarrow 0$
, but may differ by numerical prefactors of order unity. It is also important at this stage to note that we are expanding in the ratio of the pedestal width to the magnetic scale length, not in the aspect ratio of the magnetic surfaces.Footnote
2
At this point, we shall not distinguish between profiles and fluctuations in terms of frequencies and length scales. Thus, all gradients will be ordered as
![]() $L_{\bot }^{-1}$
or
$L_{\bot }^{-1}$
or
![]() $L_{\Vert }^{-1}$
. This is consistent with our next assumption: that the kinetic plasma variables (e.g. density, pressure) will have
$L_{\Vert }^{-1}$
. This is consistent with our next assumption: that the kinetic plasma variables (e.g. density, pressure) will have
![]() $O(1)$
variation. This is physically reasonable as ELMs are observed to result in filaments of hot dense plasma erupting into much colder, lower density regions. To support finite density variations on times comparable to the electron transit time
$O(1)$
variation. This is physically reasonable as ELMs are observed to result in filaments of hot dense plasma erupting into much colder, lower density regions. To support finite density variations on times comparable to the electron transit time
![]() $L_{\Vert }/v_{\text{th}_{e}}$
, we require that the electrostatic potential also support large variations
$L_{\Vert }/v_{\text{th}_{e}}$
, we require that the electrostatic potential also support large variations
Strong radial electric fields are known to play a role in pedestals, and many empirical measurements find these electric fields to be present in the absence of large plasma flows. The simplest and most plausible mechanism for this to occur is that diamagnetic flows, for the bulk ion species, are comparable to, and may sometimes cancel, the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow in the pedestal. To permit such cancellation we require the diamagnetic flow to be of the same order as the
$\boldsymbol{E}\times \boldsymbol{B}$
flow in the pedestal. To permit such cancellation we require the diamagnetic flow to be of the same order as the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow:
$\boldsymbol{E}\times \boldsymbol{B}$
flow:
with
![]() $\unicode[STIX]{x1D6FA}_{s}=Z_{s}eB/m_{s}c$
the cyclotron frequency of species
$\unicode[STIX]{x1D6FA}_{s}=Z_{s}eB/m_{s}c$
the cyclotron frequency of species
![]() $s$
,
$s$
,
![]() $c$
the speed of light and
$c$
the speed of light and
![]() $Z_{s}e$
the charge of species
$Z_{s}e$
the charge of species
![]() $s$
in terms of the unit charge
$s$
in terms of the unit charge
![]() $e$
. Note that this is also the ordering that follows from (2.3) and assuming that
$e$
. Note that this is also the ordering that follows from (2.3) and assuming that
![]() $\unicode[STIX]{x1D711}$
varies on the
$\unicode[STIX]{x1D711}$
varies on the
![]() $L_{\bot }$
scale. In this, we assume
$L_{\bot }$
scale. In this, we assume
![]() $Z_{s}\sim 1$
with respect to the
$Z_{s}\sim 1$
with respect to the
![]() $\unicode[STIX]{x1D716}\ll 1$
expansion. Thus, this ordering does not describe the behaviour of an impurity species that is so highly charged that
$\unicode[STIX]{x1D716}\ll 1$
expansion. Thus, this ordering does not describe the behaviour of an impurity species that is so highly charged that
![]() $Z_{s}\sim \unicode[STIX]{x1D716}^{-1}$
or even greater. We also will assume that all temperatures are comparable, in particular
$Z_{s}\sim \unicode[STIX]{x1D716}^{-1}$
or even greater. We also will assume that all temperatures are comparable, in particular
![]() $T_{e}\sim T_{i}$
, and will not keep track of factors of
$T_{e}\sim T_{i}$
, and will not keep track of factors of
![]() $T_{i}/T_{e}$
in our orderings.
$T_{i}/T_{e}$
in our orderings.
Next, requiring that the system be fully nonlinear, the typical decorrelation rate due to the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
nonlinearity should be comparable to the frequency of interest,
$\boldsymbol{E}\times \boldsymbol{B}$
nonlinearity should be comparable to the frequency of interest,
![]() $\unicode[STIX]{x1D714}$
:
$\unicode[STIX]{x1D714}$
:
Hence our frequencies are comparable to the diamagnetic drift frequency
![]() $\unicode[STIX]{x1D714}_{\ast }$
$\unicode[STIX]{x1D714}_{\ast }$
Using our assumption of Alfvénic time scales
and our ordering for
![]() $\unicode[STIX]{x1D6FD}$
, we have
$\unicode[STIX]{x1D6FD}$
, we have
which immediately gives
Similarly, we see that our frequencies are small compared to the cyclotron frequency
Substituting the definition of
![]() $\unicode[STIX]{x1D716}$
from (2.1) into (2.9) gives an estimate for the typical pedestal scale
$\unicode[STIX]{x1D716}$
from (2.1) into (2.9) gives an estimate for the typical pedestal scale
![]() $L_{\bot }$
in terms of
$L_{\bot }$
in terms of
![]() $L_{\Vert }\sim R$
(a typical tokamak estimate, where
$L_{\Vert }\sim R$
(a typical tokamak estimate, where
![]() $R$
is the major radius of the device) and
$R$
is the major radius of the device) and
![]() $\unicode[STIX]{x1D70C}_{i}$
:
$\unicode[STIX]{x1D70C}_{i}$
:
With this ordering in hand, we can also relate our
![]() $\unicode[STIX]{x1D716}$
to the ratio of the gyroradius to the system size:
$\unicode[STIX]{x1D716}$
to the ratio of the gyroradius to the system size:
Let us discuss the impact of the scaling (2.11). Firstly, we note that our orderings have given us a pedestal width where diamagnetic stabilisation of the ballooning mode may be important for ELM stability (Rogers & Drake Reference Rogers and Drake1999). This scaling is more optimistic for future devices than a naïve neoclassical scaling which would predict a pedestal width
![]() $L_{\bot }$
comparable to the poloidal Larmor radiusFootnote
3
$L_{\bot }$
comparable to the poloidal Larmor radiusFootnote
3
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
– in our orderings the poloidal Larmor radius is equivalent to
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
– in our orderings the poloidal Larmor radius is equivalent to
![]() $\unicode[STIX]{x1D70C}_{i}$
– but much less optimistic than the experimental results which typically show remarkably little dependence upon
$\unicode[STIX]{x1D70C}_{i}$
– but much less optimistic than the experimental results which typically show remarkably little dependence upon
![]() $\unicode[STIX]{x1D70C}_{i}$
(Beurskens et al.
Reference Beurskens, Osborne, Schneider, Wolfrum, Frassinetti, Groebner, Lomas, Nunes, Saarelma and Scannell2011).
$\unicode[STIX]{x1D70C}_{i}$
(Beurskens et al.
Reference Beurskens, Osborne, Schneider, Wolfrum, Frassinetti, Groebner, Lomas, Nunes, Saarelma and Scannell2011).
One might take these experimental data as discouragement from believing our orderings. At the same time some pedestals appear to be dominated by neoclassical transport. These two can be reconciled by noting that in current devices
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
is not much smaller than the pedestal width. In addition
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
is not much smaller than the pedestal width. In addition
![]() $\unicode[STIX]{x1D70C}_{i}^{2/3}qR$
is not much larger than
$\unicode[STIX]{x1D70C}_{i}^{2/3}qR$
is not much larger than
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
. Both of these relationships need to be well satisfied for our theory to be valid. Hence, it is very likely that current machines do not operate at a small enough value of
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D703}}$
. Both of these relationships need to be well satisfied for our theory to be valid. Hence, it is very likely that current machines do not operate at a small enough value of
![]() $\unicode[STIX]{x1D716}$
to see the asymptotic scaling in (2.11). Thus, (2.11) is a prediction for machines where
$\unicode[STIX]{x1D716}$
to see the asymptotic scaling in (2.11). Thus, (2.11) is a prediction for machines where
![]() $\unicode[STIX]{x1D70C}_{i}/R$
is smaller, with a prefactor that could be determined by simulation of the equations presented herein.
$\unicode[STIX]{x1D70C}_{i}/R$
is smaller, with a prefactor that could be determined by simulation of the equations presented herein.
We still have a couple of parameters to order with respect to
![]() $\unicode[STIX]{x1D716}$
. Firstly, we choose to retain electron parallel kinetic effects (Landau resonances etc.) upon the ELMs and so order
$\unicode[STIX]{x1D716}$
. Firstly, we choose to retain electron parallel kinetic effects (Landau resonances etc.) upon the ELMs and so order
resulting in
![]() $v_{\text{th}_{e}}\sim v_{\text{A}}$
. Secondly, in order to straddle the divide between collisional and collisionless physics, we make the maximal ordering of
$v_{\text{th}_{e}}\sim v_{\text{A}}$
. Secondly, in order to straddle the divide between collisional and collisionless physics, we make the maximal ordering of
which naturally results in
![]() $\unicode[STIX]{x1D708}_{ii}\sim v_{\text{th}_{i}}/L_{\Vert }$
. This concludes the ordering for the ELMs. Before moving on to turning these orderings into dynamical equations, we must consider the possibility of the existence of small-scale turbulence being present whilst an ELM is occurring.
$\unicode[STIX]{x1D708}_{ii}\sim v_{\text{th}_{i}}/L_{\Vert }$
. This concludes the ordering for the ELMs. Before moving on to turning these orderings into dynamical equations, we must consider the possibility of the existence of small-scale turbulence being present whilst an ELM is occurring.
2.1.1 Orderings for pedestal turbulence
Foreshadowing the results of § 3.3, it will turn out that our pedestal supports turbulent fluctuations, and the inter-ELM transport is dominated by them.Footnote 4 The effects of the turbulence are, a priori, strong enough that they could influence ELM evolution. In order to consistently include these effects, we will state here the assumptions we make about such turbulence. These assumptions will be justified in § 3.3.
The fluctuations are small, with
and
The fluctuations will have typical length scales, perpendicular to the field, given by
and along the field given by
One might worry that the large drive in the pedestal will cause turbulence from
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
to reach larger scales. However, in our ordering, this has already occurred. These fluctuations are naturally electron-scale fluctuations, forced out to ion scales by the strong drive. Indeed, the time scale of these fluctuations is assumed to be
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\sim 1$
to reach larger scales. However, in our ordering, this has already occurred. These fluctuations are naturally electron-scale fluctuations, forced out to ion scales by the strong drive. Indeed, the time scale of these fluctuations is assumed to be
As these fluctuations are faster than the ELMs and on a smaller scale, by the usual method of introducing intermediate temporal and spatial length scales we can assume the existence of an averaging operation
![]() $\langle \cdot \rangle _{\text{turb}}$
such that
$\langle \cdot \rangle _{\text{turb}}$
such that
where
![]() $\,\widetilde{f}_{s}$
is the exact (inclusive of fluctuations) distribution function. The averaged quantities are assumed to obey the orderings given above, and so we will use an undecorated notation for the averaged quantities, e.g.
$\,\widetilde{f}_{s}$
is the exact (inclusive of fluctuations) distribution function. The averaged quantities are assumed to obey the orderings given above, and so we will use an undecorated notation for the averaged quantities, e.g.
We note that, in these orderings,
![]() $\sqrt{\unicode[STIX]{x1D716}}\sim \unicode[STIX]{x1D70C}_{i}/L_{\bot }$
, and that
$\sqrt{\unicode[STIX]{x1D716}}\sim \unicode[STIX]{x1D70C}_{i}/L_{\bot }$
, and that
![]() $L_{\bot }$
is the appropriate local scale length for the physics that drives the turbulence. Thus, our orderings say that the fluctuations are small in
$L_{\bot }$
is the appropriate local scale length for the physics that drives the turbulence. Thus, our orderings say that the fluctuations are small in
![]() $\unicode[STIX]{x1D70C}^{\ast }\equiv \unicode[STIX]{x1D70C}_{i}/L_{\bot }$
. It is this relationship that will give rise to the similarity between the equations governing the turbulence and gyrokinetics.
$\unicode[STIX]{x1D70C}^{\ast }\equiv \unicode[STIX]{x1D70C}_{i}/L_{\bot }$
. It is this relationship that will give rise to the similarity between the equations governing the turbulence and gyrokinetics.
2.2 Dynamical equations
Having argued for our consistent orderings for the ELM dynamics, we now apply them to the governing equations of the plasma to obtain our reduced model. The fundamental equations we will work from are the Vlasov–Landau equation for the exact distribution function
![]() $\,\widetilde{f}_{s}$
, in terms of the exact fields
$\,\widetilde{f}_{s}$
, in terms of the exact fields
![]() $\widetilde{\boldsymbol{E}}$
and
$\widetilde{\boldsymbol{E}}$
and
![]() $\widetilde{\boldsymbol{B}}$
:
$\widetilde{\boldsymbol{B}}$
:
where
![]() $\boldsymbol{v}$
is the particle velocity and the collision operator on the right-hand side is the Landau operator. We have also added an arbitrary source
$\boldsymbol{v}$
is the particle velocity and the collision operator on the right-hand side is the Landau operator. We have also added an arbitrary source
![]() $S_{s}$
that we will keep in our inter-ELM equations (using the maximal ordering
$S_{s}$
that we will keep in our inter-ELM equations (using the maximal ordering
![]() $S_{s}\sim f_{s}v_{\text{th}_{i}}/L_{\Vert }$
so that the source can compete with inter-ELM transport). We will assume a non-relativistic plasma and also that all frequencies are low compared to the plasma frequency and all lengths long compared to the Debye length. Thus, to close the system for the fields, we have the quasineutrality constraint
$S_{s}\sim f_{s}v_{\text{th}_{i}}/L_{\Vert }$
so that the source can compete with inter-ELM transport). We will assume a non-relativistic plasma and also that all frequencies are low compared to the plasma frequency and all lengths long compared to the Debye length. Thus, to close the system for the fields, we have the quasineutrality constraint
and the pre-Maxwell Ampère’s law:
Averaging these equations over any possible fast fluctuations, we have as our fundamental kinetic equation:
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}+{\displaystyle \frac{Z_{s}e}{m_{s}}}\left(\boldsymbol{E}+\frac{1}{c}\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}=C[f_{s}]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{Z_{s}e}{m_{s}}}\left\langle \left(\unicode[STIX]{x1D6FF}\boldsymbol{E}+{\displaystyle \frac{1}{c}}\boldsymbol{v}\times \unicode[STIX]{x1D6FF}\boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}+\langle C[\unicode[STIX]{x1D6FF}f_{s}]\rangle _{\text{turb}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}}+\boldsymbol{v}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}+{\displaystyle \frac{Z_{s}e}{m_{s}}}\left(\boldsymbol{E}+\frac{1}{c}\boldsymbol{v}\times \boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}=C[f_{s}]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{Z_{s}e}{m_{s}}}\left\langle \left(\unicode[STIX]{x1D6FF}\boldsymbol{E}+{\displaystyle \frac{1}{c}}\boldsymbol{v}\times \unicode[STIX]{x1D6FF}\boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}+\langle C[\unicode[STIX]{x1D6FF}f_{s}]\rangle _{\text{turb}},\end{eqnarray}$$
and as the field equations are linear, they apply separately to the averaged and fluctuating fields.
2.2.1 The magnetic field
The first problem we tackle is that of the structure of the magnetic field. As
![]() $\unicode[STIX]{x1D6FD}\sim L_{\bot }/L_{\Vert }\ll 1$
, we naturally expect the time-dependent piece of the magnetic field to be small compared to the background, confining, field. To investigate this, we first take the
$\unicode[STIX]{x1D6FD}\sim L_{\bot }/L_{\Vert }\ll 1$
, we naturally expect the time-dependent piece of the magnetic field to be small compared to the background, confining, field. To investigate this, we first take the
![]() $m_{s}\boldsymbol{v}$
moment of (2.25), and sum over all species to obtain
$m_{s}\boldsymbol{v}$
moment of (2.25), and sum over all species to obtain
where
is the full pressure tensor of species
![]() $s$
.
$s$
.
Estimating the size of each term in this equation, the magnetic pressure force is larger than all other terms by one power of
![]() $\unicode[STIX]{x1D716}$
, due to the small
$\unicode[STIX]{x1D716}$
, due to the small
![]() $\unicode[STIX]{x1D6FD}$
. Thus, we conclude that the time-dependent piece of the magnetic field must be small compared to the background, confining, field, and so we make the split
$\unicode[STIX]{x1D6FD}$
. Thus, we conclude that the time-dependent piece of the magnetic field must be small compared to the background, confining, field, and so we make the split
where
![]() $\boldsymbol{B}_{1}\sim \unicode[STIX]{x1D716}\boldsymbol{B}_{0}$
. Note that, despite this decomposition, we will define parallel and perpendicular components of vectors with respect to the total field
$\boldsymbol{B}_{1}\sim \unicode[STIX]{x1D716}\boldsymbol{B}_{0}$
. Note that, despite this decomposition, we will define parallel and perpendicular components of vectors with respect to the total field
![]() $\boldsymbol{B}$
.
$\boldsymbol{B}$
.
With this ordering in hand, we can solve the lowest-order equation
by insisting that
![]() $B_{0}$
vary only on the long
$B_{0}$
vary only on the long
![]() $L_{\Vert }$
scale.
$L_{\Vert }$
scale.
We note that the size estimate for
![]() $\boldsymbol{B}_{1}$
is the same as what one would obtain by assuming the field follows the fluid flow and so can be displaced at most
$\boldsymbol{B}_{1}$
is the same as what one would obtain by assuming the field follows the fluid flow and so can be displaced at most
![]() $L_{\bot }$
in the perpendicular direction, and that this displacement occurs after following the perturbed field for a distance
$L_{\bot }$
in the perpendicular direction, and that this displacement occurs after following the perturbed field for a distance
![]() $L_{\Vert }$
:
$L_{\Vert }$
:
This is also the estimate one would obtain by insisting that
![]() $\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\bot }\sim \boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
.
$\boldsymbol{B}_{1}\boldsymbol{\cdot }\unicode[STIX]{x1D735}_{\bot }\sim \boldsymbol{B}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
.
Given that
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\sim L_{\Vert }^{-1}$
by definition of the parallel scale, one might be tempted to conclude that
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\sim L_{\Vert }^{-1}$
by definition of the parallel scale, one might be tempted to conclude that
![]() $\boldsymbol{B}_{0}$
only varies on the
$\boldsymbol{B}_{0}$
only varies on the
![]() $L_{\Vert }$
scale. However, we can still admit a large magnetic shear. That is, the tensor
$L_{\Vert }$
scale. However, we can still admit a large magnetic shear. That is, the tensor
![]() $\unicode[STIX]{x1D735}_{\bot }\boldsymbol{b}_{0}$
may have large components. As will be argued later, these cannot be as large as
$\unicode[STIX]{x1D735}_{\bot }\boldsymbol{b}_{0}$
may have large components. As will be argued later, these cannot be as large as
![]() $O(L_{\bot }^{-1})$
because it would entail an infeasibly strong electron current. However we will retain the possibility that the shear length
$O(L_{\bot }^{-1})$
because it would entail an infeasibly strong electron current. However we will retain the possibility that the shear length
![]() $L_{s}$
of
$L_{s}$
of
![]() $\boldsymbol{B}_{0}$
is as short as
$\boldsymbol{B}_{0}$
is as short as
![]() $O(\sqrt{L_{\bot }L_{\Vert }})$
.
$O(\sqrt{L_{\bot }L_{\Vert }})$
.
Given this decomposition of the magnetic field into fixed and time-dependent pieces, we introduce the vector potential
![]() $\boldsymbol{A}$
for
$\boldsymbol{A}$
for
![]() $\boldsymbol{B}_{1}$
only:
$\boldsymbol{B}_{1}$
only:
and we will work in Coulomb gauge
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{A}=0$
.
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{A}=0$
.
The piece of
![]() $\boldsymbol{B}_{1}$
that will turn out to be important is the change in the direction of the magnetic field, thus we make the natural decomposition
$\boldsymbol{B}_{1}$
that will turn out to be important is the change in the direction of the magnetic field, thus we make the natural decomposition
![]() $\boldsymbol{A}=A_{\Vert }\boldsymbol{b}+\boldsymbol{A}_{\bot }$
to find
$\boldsymbol{A}=A_{\Vert }\boldsymbol{b}+\boldsymbol{A}_{\bot }$
to find
From here on in, we will define perpendicular and parallel components of vectors with respect to the total large-scale field
![]() $\boldsymbol{B}$
, inclusive of
$\boldsymbol{B}$
, inclusive of
![]() $\boldsymbol{B}_{1}$
but not of any possible turbulent magnetic field. If we at any point we only wish to consider the static field
$\boldsymbol{B}_{1}$
but not of any possible turbulent magnetic field. If we at any point we only wish to consider the static field
![]() $\boldsymbol{B}_{0}$
we will denote that explicitly with a subscript
$\boldsymbol{B}_{0}$
we will denote that explicitly with a subscript
![]() $0$
on the appropriate terms.
$0$
on the appropriate terms.
2.2.2 Kinetic variables
It will be simplest, despite not retaining finite gyroradius effects, to follow the gyrokinetic literature and transform to guiding centre variables for our derivations. To simplify later derivations, we will also use a peculiar velocity relative to the mean
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity
$\boldsymbol{E}\times \boldsymbol{B}$
velocity
![]() $\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{u}_{\boldsymbol{E}}$
. It is important to note that
$\boldsymbol{w}=\boldsymbol{v}-\boldsymbol{u}_{\boldsymbol{E}}$
. It is important to note that
![]() $\boldsymbol{u}_{\boldsymbol{E}}=c\boldsymbol{E}\times \boldsymbol{b}/B$
is defined using the total mean
$\boldsymbol{u}_{\boldsymbol{E}}=c\boldsymbol{E}\times \boldsymbol{b}/B$
is defined using the total mean
![]() $\boldsymbol{B}$
including
$\boldsymbol{B}$
including
![]() $\boldsymbol{B}_{1}$
. Hence,
$\boldsymbol{B}_{1}$
. Hence,
![]() $w_{\Vert }=v_{\Vert }$
exactly. Thus, we move from
$w_{\Vert }=v_{\Vert }$
exactly. Thus, we move from
![]() $(\boldsymbol{r},\boldsymbol{v})$
to the Catto-transformed variables
$(\boldsymbol{r},\boldsymbol{v})$
to the Catto-transformed variables
![]() $(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D717},\unicode[STIX]{x1D70E})$
:
$(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D717},\unicode[STIX]{x1D70E})$
:
where
![]() $\unicode[STIX]{x1D717}$
is the gyrophase,
$\unicode[STIX]{x1D717}$
is the gyrophase,
![]() $\unicode[STIX]{x1D70E}$
is the sign of the parallel velocity and perpendicular and parallel components are taken with respect to the total mean magnetic field
$\unicode[STIX]{x1D70E}$
is the sign of the parallel velocity and perpendicular and parallel components are taken with respect to the total mean magnetic field
![]() $\boldsymbol{B}$
. We take the magnetic moment
$\boldsymbol{B}$
. We take the magnetic moment
![]() $\unicode[STIX]{x1D707}_{s}$
to be exact adiabatic invariant of the Larmor motion that is conserved to all orders in
$\unicode[STIX]{x1D707}_{s}$
to be exact adiabatic invariant of the Larmor motion that is conserved to all orders in
![]() $\unicode[STIX]{x1D716}$
(Kruskal Reference Kruskal1958; Berkowitz & Gardner Reference Berkowitz and Gardner1959).Footnote
5
$\unicode[STIX]{x1D716}$
(Kruskal Reference Kruskal1958; Berkowitz & Gardner Reference Berkowitz and Gardner1959).Footnote
5
Finally, the gyrophase
![]() $\unicode[STIX]{x1D717}$
is defined by
$\unicode[STIX]{x1D717}$
is defined by
where
![]() $\boldsymbol{e}_{1}$
and
$\boldsymbol{e}_{1}$
and
![]() $\boldsymbol{e}_{2}$
are mutually orthogonal basis vectors that satisfy
$\boldsymbol{e}_{2}$
are mutually orthogonal basis vectors that satisfy
![]() $\boldsymbol{b}=\boldsymbol{e}_{2}\times \boldsymbol{e}_{1}$
$\boldsymbol{b}=\boldsymbol{e}_{2}\times \boldsymbol{e}_{1}$
We will find it convenient to average over this gyrophase at various points in this work. All of these gyroaverages are taken at constant
![]() $\boldsymbol{R}_{s}$
,
$\boldsymbol{R}_{s}$
,
![]() $\unicode[STIX]{x1D700}_{s}$
and
$\unicode[STIX]{x1D700}_{s}$
and
![]() $\unicode[STIX]{x1D707}_{s}$
; we denote the gyroaverage by
$\unicode[STIX]{x1D707}_{s}$
; we denote the gyroaverage by
We will also occasionally need a gyroaverage at fixed
![]() $\boldsymbol{r}$
,
$\boldsymbol{r}$
,
![]() $w_{\Vert }$
,
$w_{\Vert }$
,
![]() $w_{\bot }$
, which is denoted by
$w_{\bot }$
, which is denoted by
The gyroaveraged (at fixed
![]() $\boldsymbol{R}_{s}$
) time derivatives of the gyrokinetic variables are calculated in appendix A, and are found to be (cf. (A 3) and (A 5))
$\boldsymbol{R}_{s}$
) time derivatives of the gyrokinetic variables are calculated in appendix A, and are found to be (cf. (A 3) and (A 5))
2.2.3 Kinetic equations
Rewriting (2.25) in the above variables, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}}+\dot{\boldsymbol{R}}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+\dot{\unicode[STIX]{x1D700}}_{s}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\dot{\unicode[STIX]{x1D717}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}=C\left[f_{s}\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{Z_{s}e}{m_{s}}}\left\langle \left(\unicode[STIX]{x1D6FF}\boldsymbol{E}+{\displaystyle \frac{1}{c}}\boldsymbol{v}\times \unicode[STIX]{x1D6FF}\boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}+\left\langle C\left[\unicode[STIX]{x1D6FF}f_{s}\right]\right\rangle _{\text{turb}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}t}}+\dot{\boldsymbol{R}}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+\dot{\unicode[STIX]{x1D700}}_{s}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\dot{\unicode[STIX]{x1D717}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}=C\left[f_{s}\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{Z_{s}e}{m_{s}}}\left\langle \left(\unicode[STIX]{x1D6FF}\boldsymbol{E}+{\displaystyle \frac{1}{c}}\boldsymbol{v}\times \unicode[STIX]{x1D6FF}\boldsymbol{B}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}+\left\langle C\left[\unicode[STIX]{x1D6FF}f_{s}\right]\right\rangle _{\text{turb}}.\end{eqnarray}$$
Applying our ordering for the ELM dynamics to this equation, we immediately see that the lowest-order equation is
Thus, both ions and electrons are immediately found to be gyrotropic at fixed
![]() $\boldsymbol{R}_{s}$
. The size of the gyrophase-dependent corrections differs between species and so the accuracy of this statement is
$\boldsymbol{R}_{s}$
. The size of the gyrophase-dependent corrections differs between species and so the accuracy of this statement is
Continuing to higher order in our expansion of (2.42), we find the kinetic equation for the electrons
where we note that the fluctuations from the pedestal turbulence are not strong enough to affect
![]() $f_{e}$
on this time scale. This kinetic equation can, in principle, have solutions with a non-zero parallel flow. This would, naturally, be of order
$f_{e}$
on this time scale. This kinetic equation can, in principle, have solutions with a non-zero parallel flow. This would, naturally, be of order
![]() $n_{e}v_{\text{th}_{e}}$
. Such a strong parallel flow is prohibited for two reasons. Firstly, the parallel current, estimated from Ampère’s law and using the scaling for the magnetic shear posited above, results in
$n_{e}v_{\text{th}_{e}}$
. Such a strong parallel flow is prohibited for two reasons. Firstly, the parallel current, estimated from Ampère’s law and using the scaling for the magnetic shear posited above, results in
which is inconsistent with a strong electron flow (because
![]() $j_{\Vert }\sim en_{e}u_{\Vert e}$
). Secondly, electron and ion velocities which have a relative drift comparable to the electron thermal speed are strongly unstable to Debye-scale fluctuations (Jackson Reference Jackson1960). Thus, we limit ourselves to only considering solutions to (2.45) that have no parallel flow (as this equation is correct only to lowest order in
$j_{\Vert }\sim en_{e}u_{\Vert e}$
). Secondly, electron and ion velocities which have a relative drift comparable to the electron thermal speed are strongly unstable to Debye-scale fluctuations (Jackson Reference Jackson1960). Thus, we limit ourselves to only considering solutions to (2.45) that have no parallel flow (as this equation is correct only to lowest order in
![]() $\sqrt{\unicode[STIX]{x1D716}}$
the vanishing of the flow to this order simply means that the electron flow is at most comparable to the ion thermal speed). The constraint equation is simply the
$\sqrt{\unicode[STIX]{x1D716}}$
the vanishing of the flow to this order simply means that the electron flow is at most comparable to the ion thermal speed). The constraint equation is simply the
![]() $w_{\Vert }$
moment of (2.45) and can be written as an equation for the parallel vector potential
$w_{\Vert }$
moment of (2.45) and can be written as an equation for the parallel vector potential
![]() $A_{\Vert }$
:
$A_{\Vert }$
:
Note that we can neglect the time derivative of
![]() $f_{e}$
because the electron momentum is negligible (due to both the small electron mass and the absence of sonic electron flows) and the integral of the collision operator can be estimated as
$f_{e}$
because the electron momentum is negligible (due to both the small electron mass and the absence of sonic electron flows) and the integral of the collision operator can be estimated as
which is
![]() $\sqrt{\unicode[STIX]{x1D716}}$
smaller than the terms in (2.47).
$\sqrt{\unicode[STIX]{x1D716}}$
smaller than the terms in (2.47).
For the ions, we have the simpler kinetic equation
so the ions are moved by the plasma flow, but do not spread thermally along field lines and neither accelerate nor collide in one Alfvén time. This is easily seen to be correct as all ion time scales (such as the ion streaming time, or ion–ion collision time) are small compared to the Alfvén time (or the electron–electron collision time).
Finally, as we know that the distribution functions are independent of gyrophase to leading order (cf. 2.44), we have that
where the perpendicular and parallel pressures have their usual definitions
respectively, and so the pressure tensors are also gyrotropic to leading order (the off-diagonal terms are computed later in appendix B). Hence we can now write the largest non-zero part of the momentum equation (2.26) as
which determines the time-dependent part of the total field strength.
We now have equations for the distribution functions, and the two fields that comprise
![]() $\boldsymbol{B}_{1}$
. All that remains is to derive an equation for
$\boldsymbol{B}_{1}$
. All that remains is to derive an equation for
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
2.2.4 The vorticity equation
As is common to many long-wavelength theories of a magnetised plasma, the electrostatic potential is determined from the plasma vorticity equation. This is derived in appendix B, with the final result that
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}\frac{n_{s}m_{s}}{B}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-\frac{j_{\Vert }\boldsymbol{b}}{c}\left(1-4\unicode[STIX]{x03C0}{\displaystyle \frac{p_{\Vert }-p_{\bot }}{B^{2}}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}_{0}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}}{B}}(p_{\Vert }-p_{\bot })\right]+\unicode[STIX]{x1D71B},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}\frac{n_{s}m_{s}}{B}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-\frac{j_{\Vert }\boldsymbol{b}}{c}\left(1-4\unicode[STIX]{x03C0}{\displaystyle \frac{p_{\Vert }-p_{\bot }}{B^{2}}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}_{0}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}}{B}}(p_{\Vert }-p_{\bot })\right]+\unicode[STIX]{x1D71B},\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D71B}$
is the possible contribution from turbulence, whose explicit expression is
$\unicode[STIX]{x1D71B}$
is the possible contribution from turbulence, whose explicit expression is
The parallel current in (2.53) is found from Ampère’s law:
The first term of this expression is due to the shear of the confining field. This first term can be large when compared to the second, and thus the lowest order of (2.53) is
Taking the time-dependent piece of this equation, we have that
If we assume that
![]() $\boldsymbol{B}_{0}$
has magnetic surfaces labelled by
$\boldsymbol{B}_{0}$
has magnetic surfaces labelled by
![]() $\unicode[STIX]{x1D713}_{0}$
then this becomes a constraint on the shear of
$\unicode[STIX]{x1D713}_{0}$
then this becomes a constraint on the shear of
![]() $\boldsymbol{B}_{0}$
:
$\boldsymbol{B}_{0}$
:
and, from the time-independent piece of (2.56), we discover that
so either
![]() $K(\unicode[STIX]{x1D713}_{0})$
is constant on the spatial scale
$K(\unicode[STIX]{x1D713}_{0})$
is constant on the spatial scale
![]() $L_{\bot }$
or there are exact surfaces and
$L_{\bot }$
or there are exact surfaces and
![]() $K=K(\unicode[STIX]{x1D713})$
. If
$K=K(\unicode[STIX]{x1D713})$
. If
![]() $K$
is approximately constant, then we have a strong, but unvarying shear across the pedestal. If the field
$K$
is approximately constant, then we have a strong, but unvarying shear across the pedestal. If the field
![]() $\boldsymbol{B}_{0}$
does not have surfaces then naturally such a large shear is forbidden and the solution of these constraints is
$\boldsymbol{B}_{0}$
does not have surfaces then naturally such a large shear is forbidden and the solution of these constraints is
![]() $K=0$
.
$K=0$
.
Let us discuss the physics contained in this vorticity equation. The motion of the filamentary structures, related to the inertial term on the left-hand side of (2.53) is driven by gradients of the parallel current in
![]() $\boldsymbol{B}_{0}$
(kink-mode drive) and gradients in the plasma pressure (interchange-mode drive). The part of
$\boldsymbol{B}_{0}$
(kink-mode drive) and gradients in the plasma pressure (interchange-mode drive). The part of
![]() $j_{\Vert }$
from
$j_{\Vert }$
from
![]() $\boldsymbol{B}_{1}$
represents the opposition of such motion due to field-line bending. The combination of interchange drive and field-line bending gives rise to the usual ballooning-mode physics. Thus we have all the necessary ingredients for nonlinear peeling-ballooning modes.
$\boldsymbol{B}_{1}$
represents the opposition of such motion due to field-line bending. The combination of interchange drive and field-line bending gives rise to the usual ballooning-mode physics. Thus we have all the necessary ingredients for nonlinear peeling-ballooning modes.
We also wish to note that this vorticity equation, although in a different form, is consistent with the collisional one derived in Simakov & Catto (Reference Simakov and Catto2003). This can be seen most clearly by using (D2) of Simakov & Catto (Reference Simakov and Catto2003) in (69) and (70) of the same paper. This gives the following vorticity equation
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+\frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-\frac{j_{\Vert }\boldsymbol{b}}{c}\left(1-{\displaystyle \frac{4\unicode[STIX]{x03C0}\unicode[STIX]{x03C0}_{ci}}{B^{2}}}\right)-\left(p_{i}+p_{e}-{\displaystyle \frac{1}{3}}\unicode[STIX]{x03C0}_{ci}\right)\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}\unicode[STIX]{x03C0}_{ci}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+\frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-\frac{j_{\Vert }\boldsymbol{b}}{c}\left(1-{\displaystyle \frac{4\unicode[STIX]{x03C0}\unicode[STIX]{x03C0}_{ci}}{B^{2}}}\right)-\left(p_{i}+p_{e}-{\displaystyle \frac{1}{3}}\unicode[STIX]{x03C0}_{ci}\right)\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}\unicode[STIX]{x03C0}_{ci}\right],\end{eqnarray}$$
where we have used the identity (B 14) from appendix B to rewrite the term involving the ion parallel viscosity. All notation is ours, except for
![]() $\unicode[STIX]{x03C0}_{ci}$
which is defined in (14) of Simakov & Catto (Reference Simakov and Catto2003). Using the orderings of Simakov & Catto (Reference Simakov and Catto2003), the terms involving
$\unicode[STIX]{x03C0}_{ci}$
which is defined in (14) of Simakov & Catto (Reference Simakov and Catto2003). Using the orderings of Simakov & Catto (Reference Simakov and Catto2003), the terms involving
![]() $\unicode[STIX]{x03C0}_{ci}$
are
$\unicode[STIX]{x03C0}_{ci}$
are
![]() $O(p_{i}\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x0394}_{i}/L_{\Vert }B\unicode[STIX]{x1D716})$
and so can be neglected compared to the terms only involving the pressure (by using the second inequality of (7) of Simakov & Catto (Reference Simakov and Catto2003)).
$O(p_{i}\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x0394}_{i}/L_{\Vert }B\unicode[STIX]{x1D716})$
and so can be neglected compared to the terms only involving the pressure (by using the second inequality of (7) of Simakov & Catto (Reference Simakov and Catto2003)).
Comparing this to our vorticity equation, we see that they match if, as well as taking the collisional limit of our equations (which removes the electron pressure anisotropy from our vorticity equation), one also assumes that the initial ion pressure is isotropic. Thus we include the same Alfvénic physics as Catto–Simakov.
We also discuss the difference of our vorticity equation with those found in reduced Braginskii models (Zeiler et al. Reference Zeiler, Drake and Rogers1997; Ricci et al. Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012). Taking the vorticity equation in Ricci et al. (Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012) as the most modern and complete model currently in use, we see that we retain the diamagnetic contributions to the vorticity, but not the ion-sound contributions, which are small in our orderings. We anticipate that this is the correct trade-off for ELM filaments as they are often observed to be both narrow and extremely rapid.
Finally, we should discuss the potential contribution from small-scale turbulence. This contribution is exactly analogous to the Reynold’s stress generated by electrostatic gyrokinetic turbulence. Indeed, we will find later that the equations this turbulence obeys are reminiscent of gyrokinetics. Because of this, absent symmetry breaking effects, this stress may turn out to be small (Parra, Barnes & Peeters Reference Parra, Barnes and Peeters2011). However, until calculations and simulations confirm this, we retain this term as it is formally of the required size.
2.3 Summary of the ELM model
The complete kinetic model for ELM-like behaviour on the fast, Alfvénic time scale is as follows
(i) Electron and ion distribution functions are determined from (2.45) and (2.49), respectively.
(ii) The vector potential for
 $\boldsymbol{B}_{1}$
,
$\boldsymbol{B}_{1}$
,
 $A_{\Vert }$
, is determined from (2.47).
$A_{\Vert }$
, is determined from (2.47).(iii) The electrostatic potential
 $\unicode[STIX]{x1D711}$
is determined from the vorticity equation (2.53), in which the pressure tensors are given by moments of the distribution functions we have already calculated.
$\unicode[STIX]{x1D711}$
is determined from the vorticity equation (2.53), in which the pressure tensors are given by moments of the distribution functions we have already calculated.(iv) The turbulent contribution to the vorticity equation
 $\unicode[STIX]{x1D71B}$
is defined by (2.54), where the fluctuations are calculated from the equations given in § 3.3.
$\unicode[STIX]{x1D71B}$
is defined by (2.54), where the fluctuations are calculated from the equations given in § 3.3.
These equations should be solved in an annular domain of closed field lines, with periodic parallel boundary conditions and static Dirichlet boundary conditions for
![]() $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
![]() $A_{\Vert }$
on the boundaries, such that
$A_{\Vert }$
on the boundaries, such that
![]() $\boldsymbol{u}_{\boldsymbol{E}}$
and
$\boldsymbol{u}_{\boldsymbol{E}}$
and
![]() $\boldsymbol{b}$
are tangential to the boundaries. This is achieved by taking the boundaries sufficiently far from the ELM that no plasma seeks to erupt out of the domain. Static boundary conditions are naturally appropriate as the time variation of fields outside of the ELM region is small compared to the time scale of the ELM.
$\boldsymbol{b}$
are tangential to the boundaries. This is achieved by taking the boundaries sufficiently far from the ELM that no plasma seeks to erupt out of the domain. Static boundary conditions are naturally appropriate as the time variation of fields outside of the ELM region is small compared to the time scale of the ELM.
3 Building up: inter-ELM pedestal evolution
The equations presented in the preceding section describe the rapid evolution of the pedestal region during an ELM. This rapid evolution will rearrange field lines and the plasma pressure profiles but does not itself contain the physics that would relax these profiles after an ELM. Nor do they contain the physics that builds up the density and temperature profiles between ELMs. For this, we need to consider what happens when the only solutions to the ELM equations are stationary.
To achieve this, we will first, in § 3.1 build up a set of orderings for the slow behaviour of the plasma. Then we will derive equations embodying such orderings. We will show that these equations naturally require stationary solutions to our ELM equations, which were summarised above in § 2.3. This proves one major part of self-consistency. The final piece of the puzzle will arrive in § 3.3 where we show that small-scale fluctuations, consistent with slab-like electron temperature gradient-driven (ETG) or microtearing (MTM) turbulence, drive the inter-ELM transport through our pedestal. We will also confirm the result asserted above, that this turbulence is strong enough to provide the required transport but only affects ELM dynamics in a limited way.
3.1 Inter-ELM orderings
We must now re-evaluate our orderings to accommodate the slow inter-ELM behaviour. We retain the orderings on
![]() $L_{\bot }/L_{\Vert }$
,
$L_{\bot }/L_{\Vert }$
,
![]() $\unicode[STIX]{x1D70C}_{i}/L_{\bot }$
,
$\unicode[STIX]{x1D70C}_{i}/L_{\bot }$
,
![]() $\unicode[STIX]{x1D6FD}$
,
$\unicode[STIX]{x1D6FD}$
,
![]() $m_{e}/m_{i}$
, and collisionalities from § 2.1. However, we now wish to accommodate frequencies on the ion-sound time scale,
$m_{e}/m_{i}$
, and collisionalities from § 2.1. However, we now wish to accommodate frequencies on the ion-sound time scale,
![]() $\unicode[STIX]{x1D714}\sim v_{\text{th}_{i}}/L_{\Vert }$
.
$\unicode[STIX]{x1D714}\sim v_{\text{th}_{i}}/L_{\Vert }$
.
In order to do this, we need to slow down the nonlinear time scales due to the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
motion (
$\boldsymbol{E}\times \boldsymbol{B}$
motion (
![]() $\unicode[STIX]{x1D714}_{NL}\sim \boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
and due to diamagnetic effects
$\unicode[STIX]{x1D714}_{NL}\sim \boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
and due to diamagnetic effects
![]() $\unicode[STIX]{x1D714}_{NL}\sim \boldsymbol{b}\times \unicode[STIX]{x1D735}p\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
). We manage this by introducing a new length scale
$\unicode[STIX]{x1D714}_{NL}\sim \boldsymbol{b}\times \unicode[STIX]{x1D735}p\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
). We manage this by introducing a new length scale
![]() $L_{\wedge }\sim \sqrt{L_{\bot }L_{\Vert }}\sim \sqrt{\unicode[STIX]{x1D716}}L_{\Vert }$
. We assume that in the plane perpendicular to the magnetic field we can identify a fast direction, where the typical length scales are
$L_{\wedge }\sim \sqrt{L_{\bot }L_{\Vert }}\sim \sqrt{\unicode[STIX]{x1D716}}L_{\Vert }$
. We assume that in the plane perpendicular to the magnetic field we can identify a fast direction, where the typical length scales are
![]() $L_{\bot }$
, and a slow direction, where the typical length scales are
$L_{\bot }$
, and a slow direction, where the typical length scales are
![]() $L_{\wedge }$
. In a pedestal this is naturally given by the radial and the in-surface perpendicular directions respectively (if one views the poloidal coordinate as the distance along a field line, then this slow direction is the toroidal direction).
$L_{\wedge }$
. In a pedestal this is naturally given by the radial and the in-surface perpendicular directions respectively (if one views the poloidal coordinate as the distance along a field line, then this slow direction is the toroidal direction).
Under this assumption, we see that all the nonlinearities can be written in the form
where we have used the fact that the derivatives cannot both be in the fast direction.
With this estimate in hand, we see that
as required.
No other ordering changes are required. We expect this set of equations to model the equilibrium and any possible coherent oscillation of the edge pedestal. Such coherent oscillations, with frequencies comparable to the local acoustic frequency, are thought to be important in novel modes of tokamak operation (Snipes et al. Reference Snipes, Labombard, Greenwald, Hutchinson, Irby, Lin, Mazurenko and Porkolab2001; Burrell et al. Reference Burrell, Austin, Brennan, DeBoo, Doyle, Gohil, Greenfield, Groebner, Lao and Luce2002).
We now revisit and justify the turbulence orderings introduced earlier. To distinguish scales relating to the fluctuations from the scales of the pedestal itself, we will use
![]() $k_{\bot }$
to denote typical perpendicular wavenumbers, and
$k_{\bot }$
to denote typical perpendicular wavenumbers, and
![]() $k_{\Vert }$
typical parallel wavenumbers. The only length scales smaller than
$k_{\Vert }$
typical parallel wavenumbers. The only length scales smaller than
![]() $L_{\bot }$
available to us are the gyroradii, and so we assume that the turbulence is predominantly at scales comparable to the ion gyroradius
$L_{\bot }$
available to us are the gyroradii, and so we assume that the turbulence is predominantly at scales comparable to the ion gyroradius
and because of our ordering for
![]() $\unicode[STIX]{x1D6FD}$
and the mass ratio, this means that turbulent scales are also comparable to the electron skin depth
$\unicode[STIX]{x1D6FD}$
and the mass ratio, this means that turbulent scales are also comparable to the electron skin depth
![]() $d_{e}=c/\unicode[STIX]{x1D714}_{pe}$
:
$d_{e}=c/\unicode[STIX]{x1D714}_{pe}$
:
Making a mixing length estimate for the amplitude of this turbulence we see that
This is also exactly the ordering required to balance the nonlinear turnover rate with the
![]() $\unicode[STIX]{x1D714}_{\ast }$
-drive:
$\unicode[STIX]{x1D714}_{\ast }$
-drive:
and
Both of these frequencies are comparable to
![]() $v_{\text{th}_{i}}/L_{\bot }$
. If this turbulence is mainly mediated by electrons, as in ETG or MTM turbulence, then the frequency sets a typical parallel length scale by
$v_{\text{th}_{i}}/L_{\bot }$
. If this turbulence is mainly mediated by electrons, as in ETG or MTM turbulence, then the frequency sets a typical parallel length scale by
This means that we have
![]() $k_{\Vert }L_{\Vert }\sim 1/\sqrt{\unicode[STIX]{x1D716}}\gg 1$
. This is short parallel-wavelength, slab-like turbulence. We will also assume that turbulence is as electromagnetic as our low-
$k_{\Vert }L_{\Vert }\sim 1/\sqrt{\unicode[STIX]{x1D716}}\gg 1$
. This is short parallel-wavelength, slab-like turbulence. We will also assume that turbulence is as electromagnetic as our low-
![]() $\unicode[STIX]{x1D6FD}$
assumption allows:
$\unicode[STIX]{x1D6FD}$
assumption allows:
We can also make a random-walk estimate of the transport from this turbulence
where
![]() $\unicode[STIX]{x1D70F}_{E}$
is the pedestal energy confinement time and
$\unicode[STIX]{x1D70F}_{E}$
is the pedestal energy confinement time and
![]() $D$
is a typical diffusion coefficient from our turbulence. We see that this is precisely in accord with our ordering of the inter-ELM evolution time scale.
$D$
is a typical diffusion coefficient from our turbulence. We see that this is precisely in accord with our ordering of the inter-ELM evolution time scale.
Note that our exploration of these equations does not extend to the time scale on which the confining field evolves,
![]() $\boldsymbol{B}_{0}$
is fixed throughout. This is currently no great limitation, as a pedestal that is quiescent for so long that the diffusion of current becomes important is presently beyond experimental and theoretical reach. However, this must eventually be addressed in future work.
$\boldsymbol{B}_{0}$
is fixed throughout. This is currently no great limitation, as a pedestal that is quiescent for so long that the diffusion of current becomes important is presently beyond experimental and theoretical reach. However, this must eventually be addressed in future work.
3.2 The slow dynamics of a pedestal
We use the same variables as in the prequel, and taking care to use the new ordering to estimate the size of their time derivatives we obtain
as before.
In appendix E we prove that a consistent solution to the lowest-order electron kinetic equation, in a closed-field-line region, is a Maxwellian. If this is the chosen solution, then the magnetic field is frozen into a fluid flow and the magnetic topology is fixed on the time scales of interest. Then we can assume that the field has topologically toroidal flux surfaces (denoted by
![]() $\unicode[STIX]{x1D713}$
) for all time, and we will average over them when needed.
$\unicode[STIX]{x1D713}$
) for all time, and we will average over them when needed.
The electrons are an isothermal (i.e.
![]() $T_{e}$
is constant on a flux surface) fluid, with a continuity equation for the density (cf. (E 7)):
$T_{e}$
is constant on a flux surface) fluid, with a continuity equation for the density (cf. (E 7)):
where the fluctuating velocity is given by
and an evolution equation for the temperature (see (E 10))
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{3}{2}\left\langle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left(\frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}-\frac{3}{2}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\,\left\langle en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle S_{e}^{(E)}\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{3}{2}\left\langle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left(\frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}-\frac{3}{2}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\,\left\langle en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle S_{e}^{(E)}\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
where
![]() $T_{e}=T_{e}(\unicode[STIX]{x1D713})$
. The terms on the right-hand side are easily interpreted as parallel compressional heating, turbulent ohmic heating and a possible energy source, respectively. The fluctuating distribution function
$T_{e}=T_{e}(\unicode[STIX]{x1D713})$
. The terms on the right-hand side are easily interpreted as parallel compressional heating, turbulent ohmic heating and a possible energy source, respectively. The fluctuating distribution function
![]() $\unicode[STIX]{x1D6FF}f_{e}$
is defined by (2.20), and given by the solution of (3.25) as explained in the next section.
$\unicode[STIX]{x1D6FF}f_{e}$
is defined by (2.20), and given by the solution of (3.25) as explained in the next section.
The ions obey a drift-kinetic equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)f_{i}-Z_{i}ew_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{i}}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle {\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\,h_{i}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\,C[f_{i}]+S_{i},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)f_{i}-Z_{i}ew_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{i}}}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle {\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\,h_{i}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \qquad =\,C[f_{i}]+S_{i},\end{eqnarray}$$
in which the fluctuating ion distribution function
![]() $h_{i}$
is defined by (3.24) and given by the solution of (3.23) as described in § 3.3.
$h_{i}$
is defined by (3.24) and given by the solution of (3.23) as described in § 3.3.
The fluctuating magnetic field is given by the lowest-order vorticity equation
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \left(\boldsymbol{B}_{0}+\boldsymbol{b}_{0}\times \unicode[STIX]{x1D735}A_{\Vert }\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{1}{B}}\unicode[STIX]{x1D6FB}_{\bot }^{2}A_{\Vert }-\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,4\unicode[STIX]{x03C0}\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}_{0}}{B}}\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{\bot }+{\displaystyle \frac{4\unicode[STIX]{x03C0}}{B}}\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(p_{\Vert }-p_{\bot }).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle \left(\boldsymbol{B}_{0}+\boldsymbol{b}_{0}\times \unicode[STIX]{x1D735}A_{\Vert }\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{1}{B}}\unicode[STIX]{x1D6FB}_{\bot }^{2}A_{\Vert }-\boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,4\unicode[STIX]{x03C0}\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}_{0}}{B}}\right)\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{\bot }+{\displaystyle \frac{4\unicode[STIX]{x03C0}}{B}}\unicode[STIX]{x1D735}\times \boldsymbol{b}_{0}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(p_{\Vert }-p_{\bot }).\end{eqnarray}$$
Equivalently, (3.18) is simply the constraint that the ELM time scale vorticity equation (2.53) has zero-vorticity solutions. The fluctuating
![]() $A_{\Vert }$
then determines the parallel electron flow via Ampère’s law
$A_{\Vert }$
then determines the parallel electron flow via Ampère’s law
with the sum on the right-hand side being over all ion species. We can then use (E 5), which is
to find the electrostatic potential up to a flux function
![]() $\overline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D713})$
.
$\overline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D713})$
.
Finally, the flux-surface average of the vorticity equation gives us the equation that determines
![]() $\overline{\unicode[STIX]{x1D711}}$
:
$\overline{\unicode[STIX]{x1D711}}$
:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}\frac{n_{s}m_{s}}{B}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left(\frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle =\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\mathop{\sum }_{s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \mathop{\sum }_{s}{\displaystyle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]q_{\Vert s}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle \unicode[STIX]{x1D71B}\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}\frac{n_{s}m_{s}}{B}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left(\frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle =\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\mathop{\sum }_{s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \mathop{\sum }_{s}{\displaystyle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]q_{\Vert s}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle \unicode[STIX]{x1D71B}\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
where
with the definition of turbulent vorticity
![]() $\unicode[STIX]{x1D71B}$
from (2.54).
$\unicode[STIX]{x1D71B}$
from (2.54).
Let us pause and comment on these equations for a moment. These equations live a double life. Firstly, they are transport equations, with fluxes given by averages over the pedestal turbulence. Secondly, they support sound waves and their relatives like the geodesic acoustic mode (GAM). As these are on the same time scale, the interplay between poloidally inhomogeneous turbulence and the sound waves that such inhomogeneity can excite may result in interesting physics. Equation (3.18) gives the response of the magnetic field to this transport, and is in effect the constraint that the field-line-bending forces always balance pressure forces so no Alfvén waves can be excited.
In this system, transport occurs on the same time scale that poloidal flows are damped by parallel viscosity. Thus, this system can potentially support Stringer spin-up (Stringer Reference Stringer1969; Rosenbluth & Taylor Reference Rosenbluth and Taylor1969). This mechanism has been thought to play a role in the L–H transition (Hassam et al. Reference Hassam, Antonsen, Drake and Liu1991). Indeed, investigating the behaviour of the large poloidal flows that our equations can support will be a key point of future work.
3.3 Pedestal turbulence
Finally, we come to the equations governing the turbulence in the pedestal. These are derived in § E.2, by systematically expanding the fluctuating part of (2.22) in accordance with the orderings of § 2.1.1. This derivation is standard, and closely resembles that of gyrokinetics. Thus, we leave the derivations to § E.2, and only present the results here.
The ions obey a simple kinetic equation:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right)h_{i}+{\displaystyle \frac{c}{B}}\left\{\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}.,h_{i}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right)Z_{i}e\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{i}}}-{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{i},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right)h_{i}+{\displaystyle \frac{c}{B}}\left\{\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}.,h_{i}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right)Z_{i}e\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{i}}}-{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{i},\end{eqnarray}$$
where
![]() $\boldsymbol{u}_{\boldsymbol{E}}$
is the
$\boldsymbol{u}_{\boldsymbol{E}}$
is the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity defined with the large-scale potential
$\boldsymbol{E}\times \boldsymbol{B}$
velocity defined with the large-scale potential
![]() $\unicode[STIX]{x1D711}$
, obtained from the equations in the previous section. Similarly,
$\unicode[STIX]{x1D711}$
, obtained from the equations in the previous section. Similarly,
![]() $f_{i}$
is the large-scale distribution function. In this context these fields are static, and they can be handled exactly the same as the Maxwellian backgrounds in local gyrokinetic flux-tube codes. Finally,
$f_{i}$
is the large-scale distribution function. In this context these fields are static, and they can be handled exactly the same as the Maxwellian backgrounds in local gyrokinetic flux-tube codes. Finally,
![]() $h_{i}$
is the non-adiabatic part of the ion distribution function
$h_{i}$
is the non-adiabatic part of the ion distribution function
This equation is easily seen to be the same as the slab-geometry gyrokinetic equation around a non-Maxwellian background, if one were to neglect ion-sound effects (cf. (Frieman & Chen Reference Frieman and Chen1982; Abel et al. Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013)).
The electrons also obey a gyrokinetic equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right)h_{e}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h_{e}+{\displaystyle \frac{c}{B}}\left\{\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}.,h_{e}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right){\displaystyle \frac{e\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}}{T_{e}}}f_{e}-C\left[h_{e}\right]-\frac{c}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{e},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right)h_{e}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}h_{e}+{\displaystyle \frac{c}{B}}\left\{\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}.,h_{e}\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right){\displaystyle \frac{e\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}}{T_{e}}}f_{e}-C\left[h_{e}\right]-\frac{c}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{e},\end{eqnarray}$$
where
as
![]() $f_{e}$
is Maxwellian, and
$f_{e}$
is Maxwellian, and
These two equations are coupled with the following two field equations. Firstly, the quasineutrality condition,
in which the sum on the left-hand side is taken over all ion species. Secondly, the parallel (to
![]() $\boldsymbol{b}$
but not
$\boldsymbol{b}$
but not
![]() $\boldsymbol{b}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
) component of Ampère’s law
$\boldsymbol{b}+\unicode[STIX]{x1D6FF}\boldsymbol{B}$
) component of Ampère’s law
where the ions do not participate due to the high frequency of the fluctuations. Perpendicular pressure balance obtains, and allows one to calculate turbulent fluctuations in the field strength,
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, but these do not react back upon the turbulence, nor do they contribute to the ensuing transport. This is easy to see as the drift arising from
$\unicode[STIX]{x1D6FF}B_{\Vert }=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D6FF}\boldsymbol{B}$
, but these do not react back upon the turbulence, nor do they contribute to the ensuing transport. This is easy to see as the drift arising from
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }$
is
$\unicode[STIX]{x1D6FF}B_{\Vert }$
is
![]() $O(\unicode[STIX]{x1D716}v_{\text{th}_{i}})$
whereas the
$O(\unicode[STIX]{x1D716}v_{\text{th}_{i}})$
whereas the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
drift due to
$\boldsymbol{E}\times \boldsymbol{B}$
drift due to
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
is
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
is
![]() $O(\unicode[STIX]{x1D716}^{1/2}v_{\text{th}_{i}})$
.
$O(\unicode[STIX]{x1D716}^{1/2}v_{\text{th}_{i}})$
.
We should comment upon the geometry these equations should be solved in. The turbulence they describe occurs on spatial scales that are short compared to those of the pedestal profile. Hence, as in classic gyrokinetic simulations, flux-tubes with periodic perpendicular boundary conditions (Beer, Cowley & Hammett Reference Beer, Cowley and Hammett1995) are the correct setting for solving these equations. However, as the turbulence is such that the parallel correlation lengths are short compared even to the connection length, shear-periodic parallel boundary conditions are also required. Similarly, all geometric quantities that vary on the
![]() $L_{\Vert }$
scale along the field line (poloidally) should be evaluated at one point and not vary through the simulation domain. Importantly, this means that trapped-particle effects are irrelevant for this turbulence, as only a small fraction of particles have a bounce point in any given
$L_{\Vert }$
scale along the field line (poloidally) should be evaluated at one point and not vary through the simulation domain. Importantly, this means that trapped-particle effects are irrelevant for this turbulence, as only a small fraction of particles have a bounce point in any given
![]() $1/k_{\Vert }$
length of plasma. The only geometry of the field that is retained is the magnetic shear. This is easily seen by expanding the operator
$1/k_{\Vert }$
length of plasma. The only geometry of the field that is retained is the magnetic shear. This is easily seen by expanding the operator
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
around some radial point
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
around some radial point
![]() $r_{0}$
$r_{0}$
where, as
![]() $r-r_{0}\sim \unicode[STIX]{x1D6FB}_{\bot }^{-1}$
, the second term will be comparable to the first if
$r-r_{0}\sim \unicode[STIX]{x1D6FB}_{\bot }^{-1}$
, the second term will be comparable to the first if
![]() $k_{\Vert }L_{s}\sim 1$
. Referring back to our maximal estimates for the amount of magnetic shear in the pedestal, we see that this ordering is marginally satisfied. Thus, magnetic shear must be retained. These simplifications should render simulation of these equations simpler than current methods for simulating pedestal-relevant turbulence.
$k_{\Vert }L_{s}\sim 1$
. Referring back to our maximal estimates for the amount of magnetic shear in the pedestal, we see that this ordering is marginally satisfied. Thus, magnetic shear must be retained. These simplifications should render simulation of these equations simpler than current methods for simulating pedestal-relevant turbulence.
This set of equations is also interesting for several reasons. It is a strict superset of the equations of Zocco & Schekochihin (Reference Zocco and Schekochihin2011) which comprise a popular reduced model for studying reconnection. The equations also contain equations used to study microtearing physics in Zocco et al. (Reference Zocco, Loureiro, Dickinson, Numata and Roach2015). In the limit of weak magnetic shear, and weak background ion gradients, our equations reduce to a model that has been shown to support strong electromagnetic ETG turbulence, due to an inverse cascade process (L. Milanese et al. 2017, Private communication). This strongly suggests our equations support the turbulent processes believed to be most important in the pedestal (Saarelma et al. Reference Saarelma, Beurskens, Dickinson, Frassinetti, Leyland and Roach2013; Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Valanju, Jenko, Told, G??rler and Saarelma2016; Hillesheim et al. Reference Hillesheim, Dickinson, Roach, Saarelma, Scannell, Kirk, Crocker, Peebles and Meyer2016; Hatch et al. Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017).
3.4 Summary
Our inter-ELM equations consist of two time scales. Firstly the slow time scale equations, which comprise the following:
(i) (3.14) and (3.16) to determine the electron density
 $n_{e}$
and temperature
$n_{e}$
and temperature
 $T_{e}$
respectively,
$T_{e}$
respectively,(ii) (3.17) to determine
 $f_{i}$
,
$f_{i}$
,(iii) (3.18) which determines
 $A_{\Vert }$
,
$A_{\Vert }$
,(iv) (3.20), which determines
 $\unicode[STIX]{x1D711}$
up to a flux function
$\unicode[STIX]{x1D711}$
up to a flux function(v) and (3.21) that determines that flux function.
All of these equations are meant to be solved on a global annular domain containing the entire pedestal. The detailed boundary conditions will be discussed in § 4.
In some of these equations, there are terms that arise from averages over the turbulence. The turbulence is governed by the following equations:
(i) the kinetic equations, (3.23) for
 $h_{i}$
and (3.25) for
$h_{i}$
and (3.25) for
 $h_{e}$
,
$h_{e}$
,(ii) the quasineutrality condition (3.28) for
 $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
(iii) and parallel Ampère’s law (3.29) for
 $\unicode[STIX]{x1D6FF}A_{\Vert }$
.
$\unicode[STIX]{x1D6FF}A_{\Vert }$
.
There are also the relations (3.24), (3.26) and (3.27) that relate these fields to the fields that arise in the flux terms in the inter-ELM equations. As usual for coupling turbulent fluxes to a transport code, these equations should be run to a steady state and appropriately averaged to give the fluxes.
4 Betwixt and between: boundary conditions, matching and existing models
In this section, we tackle two remaining points regarding the systems of equations derived above. Firstly, how they interact, and how they couple both to core and scrape-off layer models. Then, secondly, how they compare to existing strategies for modelling this region of the plasma.
4.1 The integrated approach: coupling and boundary conditions
Having derived a full multiscale approach to the pedestal, the question naturally arises of how these equations should be coupled to each other, and to other parts of the plasma. We have a framework for physics on three disparate time scales. The fastest is the time scale of the individual turbulent fluctuations. Then comes the time scale on which ELM filaments erupt. Finally, the time scale on which transport occurs, which is the same as the acoustic time scale.
The outline of the envisioned implementation, reminiscent of the operation of multiscale core transport codes, is as follows. Given an initial pedestal profile, one tests for stability in the ELM equations. Due to the meta-stable nature of erupting ELM filaments (Cowley et al. Reference Cowley, Cowley, Henneberg and Wilson2015; Ham et al. Reference Ham, Cowley, Brochard and Wilson2016), a purely linear solver may be insufficient to evaluate the stability of the pedestal to ELMs.Footnote 6 A more robust approach is to initialise the ELM equations with the initial profile and, in addition, some specified amount of noise. One then evolves the fully nonlinear equations for a short time. Either nothing happens, if the pedestal is suitably stable, or the filaments erupt and a new equilibrium is rapidly reached. Once a situation is reached where no more evolution occurs on the fast time scale, the state is such that it is a valid initial condition for the inter-ELM equations.
The inter-ELM equations are then used to evolve the profiles on the long time scale, with fluxes given by the pedestal turbulence. We envision these equations being solved in a (topologically) annular region, with inner and outer surfaces corresponding to flux surfaces. The boundary conditions at the inner radial location is given by matching to multiscale gyrokinetics. The core is solved as in Barnes et al. (Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010), with the boundary values for the transport equations being taken from our inter-ELM pedestal profile. That profile is itself solved for with a fixed-flux boundary condition obtained from the outermost radial grid point of the gyrokinetic transport calculation. In general, this indicates that the core transport time step and the Inter-ELM time step must be taken together. However, for a steady-state situation one could envision solving the inter-ELM equations with a fixed flux given by the total heating and fuelling sources before then solving the core with a fixed value for the pedestal. The outer radial boundary condition is given, in principle, by matching to a scrape-off-layer model just inside the separatrix. We discuss the difficulties and possibilities of such matching in § 4.3. Absent an exact model to match to, we take the same ad hoc approach as Barnes et al. (Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010) and suggest fixing values for top of the scrape-off layer at the separatrix. The pedestal turbulence, which gives rise to the fluxes, is solved locally in slab-like flux tubes, as described in detail at the end of § 3.3.
Periodically during this evolution, stability in the ELM equations is checked for. If at any point the ELM equations are unstable, then one returns to the start of this procedure and evolves on the short time scale until a new equilibrium is reached. In principle this is checked every time step of the inter-ELM equations (just as MHD stability should be checked every time step of a core transport code), but hopefully heuristics can be developed to ameliorate this cost.Footnote 7 It is easy to see how this cyclical procedure would produce an ELM cycle.
Ideally, this framework would resolve the problematic issue of boundary conditions in core multiscale codes – the solution to the core transport equations is sensitive to the fixed boundary condition at the top of the pedestal. One might hope that sensitivity studies of the equations in this paper would demonstrate an insensitivity of the pedestal top temperature to conditions at the separatrix. Of course, this is mere speculation, and one may wonder, pessimistically, if sensitivity to boundary values continues all the way to a material surface.
Now, the fact that multiscale gyrokinetics has a subsidiary limit that provides a large enough heat flux to appropriately source the inter-ELM equations is not obvious. Indeed, it is not obvious that our inner boundary is even consistent with multiscale gyrokinetics. To this end we will show explicitly in the next section that these two theories can indeed be matched on to each other at the pedestal top.
4.2 Matching at the pedestal top
In this section we show that our pedestal model can be smoothly matched on to multiscale gyrokinetics. More precisely, we mean that there is a subsidiary expansion of each of these systems that results in the same set of equations. This implies that there is potentially a region in the plasma that would be well described by both multiscale gyrokinetics and the model contained in this paper. Suggestively, we will designate this location as the top of the pedestal.
In this section, we will only detail the orderings of the subsidiary expansions. Detailed calculations showing that these orderings do indeed result in the same set of equations are performed in appendix F. We begin with the expansion of multiscale gyrokinetics. This should be seen as an expansion in nearness to the pedestal. As the pedestal top is approached from the core, steepening density gradients and decreasing
![]() $\unicode[STIX]{x1D702}_{i}$
conspire to stabilise the ion-temperature-gradient (ITG) mode. Thus, we are looking at an expansion that should result in strongly driven microtearing and ETG turbulence.
$\unicode[STIX]{x1D702}_{i}$
conspire to stabilise the ion-temperature-gradient (ITG) mode. Thus, we are looking at an expansion that should result in strongly driven microtearing and ETG turbulence.
There are two main expansions we will need to do. Firstly, we will need an expansion in small Mach number to match the rapidly rotating core onto the subsonic pedestal. Secondly, in order to begin to match the pedestal, we will need a subsidiary expansion in both the mass ratio and in
![]() $\unicode[STIX]{x1D6FD}$
. This will mainly affect the equations for the fluctuations, and closely parallels the derivation in Zocco & Schekochihin (Reference Zocco and Schekochihin2011).
$\unicode[STIX]{x1D6FD}$
. This will mainly affect the equations for the fluctuations, and closely parallels the derivation in Zocco & Schekochihin (Reference Zocco and Schekochihin2011).
We do this as two subsidiary expansions, so the first expansion is that of small Mach number
![]() $M$
. We will use a naïve low-Mach-number expansion, where
$M$
. We will use a naïve low-Mach-number expansion, where
![]() $M\ll 1$
but the scale length of the flow is the same as the perpendicular scale length of all other mean quantities. Such an expansion simply results in the zero-flow limit of gyrokinetics. The resulting equations are simply the equations of section 11 of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013) with any remaining terms involving the equilibrium flow neglected. This is the same as the system of equations presented in Sugama et al. (Reference Sugama, Okamoto, Horton and Wakatani1996), except in a notation that is closer to the one used in this paper. It is this set of equations we will now expand in
$M\ll 1$
but the scale length of the flow is the same as the perpendicular scale length of all other mean quantities. Such an expansion simply results in the zero-flow limit of gyrokinetics. The resulting equations are simply the equations of section 11 of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013) with any remaining terms involving the equilibrium flow neglected. This is the same as the system of equations presented in Sugama et al. (Reference Sugama, Okamoto, Horton and Wakatani1996), except in a notation that is closer to the one used in this paper. It is this set of equations we will now expand in
![]() $\unicode[STIX]{x1D6FD}$
and
$\unicode[STIX]{x1D6FD}$
and
![]() $m_{e}/m_{i}$
.
$m_{e}/m_{i}$
.
To formalise our second subsidiary expansion, we introduce a small parameter
![]() $\unicode[STIX]{x1D709}$
, defined by
$\unicode[STIX]{x1D709}$
, defined by
We then order
where
![]() $\unicode[STIX]{x1D716}_{\text{GK}}=k_{\Vert }/k_{\bot }$
is the small parameter of gyrokinetics. Other than this rebranding, we will use the notation of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013) when discussing multiscale gyrokinetics. We retain
$\unicode[STIX]{x1D716}_{\text{GK}}=k_{\Vert }/k_{\bot }$
is the small parameter of gyrokinetics. Other than this rebranding, we will use the notation of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013) when discussing multiscale gyrokinetics. We retain
from gyrokinetics and due to our ordering for
![]() $\unicode[STIX]{x1D6FD}_{e}$
we keep the electron skin depth scale,
$\unicode[STIX]{x1D6FD}_{e}$
we keep the electron skin depth scale,
as well. With this ordering for
![]() $k_{\bot }$
, the frequencies become
$k_{\bot }$
, the frequencies become
As in (Zocco & Schekochihin Reference Zocco and Schekochihin2011) this expansion in
![]() $\unicode[STIX]{x1D6FD}$
reduces the relative importance of some electromagnetic effects. Thus, we have
$\unicode[STIX]{x1D6FD}$
reduces the relative importance of some electromagnetic effects. Thus, we have
To drive this increase in turbulent amplitude, we assume that the gradients in
![]() $F_{0s}$
are increased
$F_{0s}$
are increased
with
![]() $a$
the long equilibrium length scale, assumed to be comparable to the parallel connection length
$a$
the long equilibrium length scale, assumed to be comparable to the parallel connection length
![]() $qR$
. However, the parallel length scale of the fluctuations is now
$qR$
. However, the parallel length scale of the fluctuations is now
Note that this scaling is consistent with turbulence that has its outer scale fixed (independent of drive) around
![]() $\unicode[STIX]{x1D70C}_{i}$
such as might follow from an inverse cascade from electron scales that is broken by ion gyroscale physics (L. Milanese et al. 2017, Private communication). As the drive is increased, instead of the outer scale increasing, the frequency increases and the parallel length scale decreases due to causality. Thus, this ordering is not consistent with a naïve scaling theory of critically balanced ETG turbulence which might be expected to follow the orderings of Barnes, Parra & Schekochihin (Reference Barnes, Parra and Schekochihin2011).
$\unicode[STIX]{x1D70C}_{i}$
such as might follow from an inverse cascade from electron scales that is broken by ion gyroscale physics (L. Milanese et al. 2017, Private communication). As the drive is increased, instead of the outer scale increasing, the frequency increases and the parallel length scale decreases due to causality. Thus, this ordering is not consistent with a naïve scaling theory of critically balanced ETG turbulence which might be expected to follow the orderings of Barnes, Parra & Schekochihin (Reference Barnes, Parra and Schekochihin2011).
With our ordering, the transport time scale of such turbulence is now
As we are allowing the various scales of the equilibrium to be ordered differently (unlike normal gyrokinetics), we must consider how to handle the magnetic shear length scale
![]() $L_{s}$
. As our pedestal allows for strong shear, we take the ordering
$L_{s}$
. As our pedestal allows for strong shear, we take the ordering
such that
![]() $k_{\Vert }L_{s}\sim 1$
, which is consistent with electromagnetic microtearing turbulence.
$k_{\Vert }L_{s}\sim 1$
, which is consistent with electromagnetic microtearing turbulence.
Revisiting the collisionality estimate from above,
![]() $\unicode[STIX]{x1D708}_{ee}\sim v_{\text{th}_{e}}/qR$
, we see that our turbulence should be collisionless if our pedestal is trans-collisional. Hence, we will assume that the turbulence self-generates phase-space structure sufficient that the collision operator is retained in the resultant gyrokinetic equation.Footnote
8
This assumption of steep gradients in velocity space is needed in order that dissipation can continue to balance the turbulent fluxes in the free-energy conservation equation of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013).
$\unicode[STIX]{x1D708}_{ee}\sim v_{\text{th}_{e}}/qR$
, we see that our turbulence should be collisionless if our pedestal is trans-collisional. Hence, we will assume that the turbulence self-generates phase-space structure sufficient that the collision operator is retained in the resultant gyrokinetic equation.Footnote
8
This assumption of steep gradients in velocity space is needed in order that dissipation can continue to balance the turbulent fluxes in the free-energy conservation equation of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013).
Applying this ordering to the low-Mach-number equations of gyrokinetics results in the set of equations detailed in appendix F. We thus turn to the subsidiary ordering of our inter-ELM equations. We do not need to revisit our ELM equations as gyrokinetics assumes that the plasma is MHD stable, and so to match on to it we make the same assumption.
The subsidiary expansion we engage in should be thought of as approaching the top of the pedestal from inside the pedestal region. Perpendicular gradients are shallower than they are in the pedestal. ITG-driven turbulence is still suppressed, but the microtearing and ETG turbulence is not as strong as it is in the pedestal proper. To quantify this, we introduce a second subsidiary parameter
![]() $\unicode[STIX]{x1D701}$
to quantify our expansion of the inter-ELM equations. It is defined by
$\unicode[STIX]{x1D701}$
to quantify our expansion of the inter-ELM equations. It is defined by
This lower-amplitude turbulence naturally leads to a longer
![]() $k_{\Vert }$
for the fluctuations, obtained from a critical-balance estimate
$k_{\Vert }$
for the fluctuations, obtained from a critical-balance estimate
giving
Consistent with this reduction in turbulent amplitude is a reduction in the driving gradients (a linear scaling of
![]() $\unicode[STIX]{x1D6FF}f_{s}/f_{s}$
with driving gradient is in accord with the results of Barnes et al. (Reference Barnes, Parra and Schekochihin2011))
$\unicode[STIX]{x1D6FF}f_{s}/f_{s}$
with driving gradient is in accord with the results of Barnes et al. (Reference Barnes, Parra and Schekochihin2011))
We will order the time derivatives of the mean quantities with the modified turbulent transport time,
but we shall keep the collision time comparable to the parallel sound time.
The mean electrostatic potential is ordered so as to allow us to match up with a low-Mach-number expansion of gyrokinetics. We fix the amplitude of the potential at
![]() $T_{e}/e$
as we head towards the interior of the tokamak, but keep the scale length that of the other mean quantities:
$T_{e}/e$
as we head towards the interior of the tokamak, but keep the scale length that of the other mean quantities:
This means that the shearing rate drops with decreasing
![]() $\unicode[STIX]{x1D701}$
and so the mean flow is eliminated from our equations.
$\unicode[STIX]{x1D701}$
and so the mean flow is eliminated from our equations.
This set of orderings reproduces exactly the same set of equations as the expansion of gyrokinetics detailed above. Hence, we can confidently say that there is a physically plausible regime which is described both by gyrokinetics and by our pedestal model, and acts as a bridge between them. Operationally, we expect this region to be located at the top of a pedestal, but one could also envision using our model to embed a transport barrier region inside core gyrokinetics.
Having shown that we match on to the best tested model of core turbulence, in the next section we will discuss how our model matches on to scrape-off-layer models which are much less developed.
4.3 Matching on to the scrape-off layer
To leave the plasma and reach such a surface, one can imagine coupling the above pedestal to a collisional scrape-off-layer (SOL) model such as Catto–Simakov or GBS, where the boundary between closed and open field lines is completely contained in the SOL model. If the plasma is still hot enough to be weakly collisional at the separatrix then such a coupling may not be consistent, and further work is required. Exciting models for arbitrary collisionality scrape-off layers have recently been proposed (Jorge, Ricci & Loureiro Reference Jorge, Ricci and Loureiro2017), and matching to such models should be addressed in the future.
As yet, such an explicit matching (either collisional or collisionless) has not been performed. However, even without the explicit forms of the equations that are to be matched, we know that they must obey certain constraints. We know that they must conserve energy and particles, and as such we can envisage using the fluxes leaving the pedestal (as simulated by our equations) as boundary conditions for a scrape-off-layer model. One could also, perhaps, use the general spectrum of fluctuations in our model to initialise some noise in a scrape-off-layer code. This procedure would, of course, be fundamentally inconsistent. Consistency requires not only a smooth matching of the fluxes at the boundary, but also a matching of the mechanisms that carry that flux. Rigorous subsidiary expansions would provide a finite-width region in which both models were valid, and we could be confident in matching across this region. We leave the detailed derivation of such expansions to future work.
4.4 Existing models
Individual parts of our model are directly comparable to some parts of existing models, and we have highlighted these both in the discussion of the ELM vorticity equation in § 2.2 and in § 3.3 where we discuss pedestal turbulence. Thus, in this section, we focus on comparing our model as a whole to other approaches for simulation and modelling of the pedestal region of a tokamak.
The most successful empirical model of the pedestal is the EPED model (Snyder et al.
Reference Snyder, Wilson, Ferron, Lao, Leonard, Osborne, Turnbull, Mossessian, Murakami and Xu2002, Reference Snyder, Groebner, Hughes, Osborne, Beurskens, Leonard, Wilson and Xu2011). This combines a collisional, long-wavelength model for peeling-ballooning modes (Wilson et al.
Reference Wilson, Snyder, Huysmans and Miller2002), with an assumption that the inter-ELM turbulence is given by kinetic-ballooning modes (KBM), modelled heuristically by the infinite-
![]() $n$
ballooning stability limit. Our model improves upon this by including weakly collisional kinetic effects including electron landau damping, trapped electron physics and self-consistent diamagnetic stabilisation into the time-dependent ELM dynamics. We also have a self-consistent model of the underlying pedestal turbulence. Indeed, the assumption that the turbulence is strictly KBM in nature has recently come under scrutiny (Hatch et al.
Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017) as detailed gyrokinetic analysis lends more support to the turbulence being MTM or ETG in nature. Two-fluid simulations of ELMs with BOUT++ (Xu et al.
Reference Xu, Dudson, Snyder, Umansky, Wilson and Casper2011), which have been included in EPED, can capture some of the non-ideal effects of our model, but not the electron kinetic effects. In addition, our model makes precise the potential sources of the effects of turbulence upon the ELM dynamics.
$n$
ballooning stability limit. Our model improves upon this by including weakly collisional kinetic effects including electron landau damping, trapped electron physics and self-consistent diamagnetic stabilisation into the time-dependent ELM dynamics. We also have a self-consistent model of the underlying pedestal turbulence. Indeed, the assumption that the turbulence is strictly KBM in nature has recently come under scrutiny (Hatch et al.
Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017) as detailed gyrokinetic analysis lends more support to the turbulence being MTM or ETG in nature. Two-fluid simulations of ELMs with BOUT++ (Xu et al.
Reference Xu, Dudson, Snyder, Umansky, Wilson and Casper2011), which have been included in EPED, can capture some of the non-ideal effects of our model, but not the electron kinetic effects. In addition, our model makes precise the potential sources of the effects of turbulence upon the ELM dynamics.
More generally, two-fluid or reduced Braginskii simulations will not capture the weakly collisional physics that may be important in a hot pedestal. The most complete fluid equations are those of GBS (Ricci et al.
Reference Ricci, Halpern, Jolliet, Loizu, Mosetto, Fasoli, Furno and Theiler2012) or Catto–Simakov (Simakov & Catto Reference Simakov and Catto2003). The former of these has almost exclusively been used to study open-field-line regions, but the latter was formulated with the explicit intent of handling closed-field-line regions in pedestals. The fluid nature of the models means that they cannot capture kinetic effects that may affect ELM stability. In addition, these models do not consistently separate the sound and Alfvénic time scales, despite the low-
![]() $\unicode[STIX]{x1D6FD}$
nature of their models. Their ordering schemes do not touch on the possibility of small-scale fluctuations existing within the pedestal, but could be extended to include the turbulence model we have presented above. Indeed, the Catto–Simakov model, with turbulence and separating the two equilibrium time scales is the collisional limit of the equations we have presented.
$\unicode[STIX]{x1D6FD}$
nature of their models. Their ordering schemes do not touch on the possibility of small-scale fluctuations existing within the pedestal, but could be extended to include the turbulence model we have presented above. Indeed, the Catto–Simakov model, with turbulence and separating the two equilibrium time scales is the collisional limit of the equations we have presented.
The final approach that is considered for pedestal modelling is global full-
![]() $f$
gyrokinetics (Chang et al.
Reference Chang, Ku, Adams, DAzevedo, Chen, Cummings, Ethier, Greengard, Hahm and Hinton2006; Churchill et al.
Reference Churchill, Chang, Ku and Dominski2017). This approach promises to include all the physics, at all scales, consistently. The potential pitfalls of this approach are twofold. Firstly, the numerical requirements are extraordinary, requiring all parts of the simulation to resolve the fastest and smallest fluctuations. This may render predictive parameter scans prohibitively expensive. Secondly, by incorporating all temporal and spatial scales on the same footing, it becomes incredibly hard to extract the physics of the interaction of these scales. Our model should be much less numerically challenging, especially as the turbulence can be parallelised over the background parameters in an approach reminiscent of current core transport codes (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010). Again, because we have decoupled the filamentary dynamics from the slow sound-time dynamics and the fluctuations, we can examine each piece of the puzzle separately.
$f$
gyrokinetics (Chang et al.
Reference Chang, Ku, Adams, DAzevedo, Chen, Cummings, Ethier, Greengard, Hahm and Hinton2006; Churchill et al.
Reference Churchill, Chang, Ku and Dominski2017). This approach promises to include all the physics, at all scales, consistently. The potential pitfalls of this approach are twofold. Firstly, the numerical requirements are extraordinary, requiring all parts of the simulation to resolve the fastest and smallest fluctuations. This may render predictive parameter scans prohibitively expensive. Secondly, by incorporating all temporal and spatial scales on the same footing, it becomes incredibly hard to extract the physics of the interaction of these scales. Our model should be much less numerically challenging, especially as the turbulence can be parallelised over the background parameters in an approach reminiscent of current core transport codes (Barnes et al.
Reference Barnes, Abel, Dorland, Görler, Hammett and Jenko2010). Again, because we have decoupled the filamentary dynamics from the slow sound-time dynamics and the fluctuations, we can examine each piece of the puzzle separately.
5 Summary and conclusions
In this paper we have derived a self-consistent first-principles model for a pedestal.
The first part of the model is a trans-collisional ELM model, given by (2.45), (2.47), (2.49), (2.53) and closed with (2.31) and (2.55). This model contains the eruption of filamentary structures driven both by magnetic buoyancy forces and launched by current-driven instabilities. It is fully nonlinear and capable of dynamically evolving a filamentary structure from one equilibrium to another.
These equilibria provide the backdrop for the next part of the model. The evolution of the inter-ELM profiles. This is given by (3.14), (3.16), (3.17), (3.18), (3.20) and (3.21). This component of the framework contains the physics of sound waves, including GAMs which are often seen in the edge, poloidal spin-up, and even systematically includes turbulent transport.
These equations are, in turn, closed by a set of equations governing the turbulence that generates that transport. These are, explicitly, the set (3.23)–(3.29). This set contains the physics of strongly driven microtearing and ETG turbulence.
Future work must include exploring the equilibria of this system, with special focus on the stability of zero-flow solutions to spontaneous spin-up. In addition, the scaling of pedestal turbulence with drive parameters is a high priority – if pedestal turbulence exhibits the
![]() $(R/L_{T})^{3}$
scaling of core turbulence, then this may permit the formation of boundary layers that govern the size of ELM filaments.
$(R/L_{T})^{3}$
scaling of core turbulence, then this may permit the formation of boundary layers that govern the size of ELM filaments.
Acknowledgements
Support for I.G.A. was provided by the Princeton Center for Theoretical Science, for the initial work, and later the Framework grant for Strategic Energy Research (Dnr. 2014-5392) from Vetenskapsrådet. Discussions with G. Hammett of Princeton Plasma Physics Lab led to many of the key insights that made this work possible. The authors also thank P. Catto, F. Parra, P. Ricci, F. Militello, J. Connor, P. Helander and T. Fülöp for fascinating and productive discussions. These discussions were facilitated by the generous hospitality and material support provided by the Wolfgang Pauli Institute in Vienna and Chalmers University of Technology. This work was conducted in part within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement no. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission.
Appendix A. Time derivatives of the gyrokinetic variables
In this appendix we take the time derivatives of the variables used in the body of the paper. We start with the gyrocentre position,
where the derivative is taken along unperturbed orbits. Noting that all effects of magnetic inhomogeneity result in terms of order
![]() $v_{\text{th}_{s}}\unicode[STIX]{x1D70C}_{s}/L_{\Vert }$
, we can neglect them. Thus this becomes
$v_{\text{th}_{s}}\unicode[STIX]{x1D70C}_{s}/L_{\Vert }$
, we can neglect them. Thus this becomes
In the fast ELM ordering, the component of
![]() $\boldsymbol{u}_{\boldsymbol{E}}$
due to
$\boldsymbol{u}_{\boldsymbol{E}}$
due to
![]() $A_{\Vert }$
is
$A_{\Vert }$
is
![]() $O(\unicode[STIX]{x1D716}^{3/2}v_{\text{th}_{i}})$
. In the inter-ELM ordering it is suppressed by another factor of
$O(\unicode[STIX]{x1D716}^{3/2}v_{\text{th}_{i}})$
. In the inter-ELM ordering it is suppressed by another factor of
![]() $\unicode[STIX]{x1D716}^{1/2}$
. Hence we can neglect it. Gyroaveraging our formula is trivial, and results in
$\unicode[STIX]{x1D716}^{1/2}$
. Hence we can neglect it. Gyroaveraging our formula is trivial, and results in
as required.
The energy is also simple to handle. Working from the definition we immediately see that
Gyroaveraging gives
The magnetic moment is defined to be the exact adiabatic invariant
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D707}_{s}={\displaystyle \frac{m_{s}w_{\bot }^{2}}{2B}}-{\displaystyle \frac{m_{s}}{B}}\left[\boldsymbol{w}_{\bot }\boldsymbol{\cdot }\boldsymbol{V}_{\text{D}s}-{\displaystyle \frac{1}{\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D652}\boldsymbol{ : }\left(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{w_{\bot }^{2}}{2B\unicode[STIX]{x1D6FA}_{s}}}\left(w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}+\unicode[STIX]{x1D735}\times \boldsymbol{u}_{\boldsymbol{E}}\right)+O\left(\unicode[STIX]{x1D716}^{2}{\displaystyle \frac{m_{s}v_{\text{th}_{s}}^{2}}{2B}}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D707}_{s}={\displaystyle \frac{m_{s}w_{\bot }^{2}}{2B}}-{\displaystyle \frac{m_{s}}{B}}\left[\boldsymbol{w}_{\bot }\boldsymbol{\cdot }\boldsymbol{V}_{\text{D}s}-{\displaystyle \frac{1}{\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D652}\boldsymbol{ : }\left(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{w_{\bot }^{2}}{2B\unicode[STIX]{x1D6FA}_{s}}}\left(w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}+\unicode[STIX]{x1D735}\times \boldsymbol{u}_{\boldsymbol{E}}\right)+O\left(\unicode[STIX]{x1D716}^{2}{\displaystyle \frac{m_{s}v_{\text{th}_{s}}^{2}}{2B}}\right),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D652}$
is given by
$\unicode[STIX]{x1D652}$
is given by
This tensor is useful because it satisfies
Finally, for
![]() $\dot{\unicode[STIX]{x1D717}}$
we take the time derivative of
$\dot{\unicode[STIX]{x1D717}}$
we take the time derivative of
and find
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{Z_{s}e}{m_{s}}}\left(E_{\Vert }\boldsymbol{b}+\frac{1}{c}\boldsymbol{w}\times \boldsymbol{B}\right)={\displaystyle \frac{\text{d}w_{\Vert }}{\text{d}t}}\boldsymbol{b}+w_{\Vert }\left({\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{b}}{\unicode[STIX]{x2202}t}}+\boldsymbol{w}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)+{\displaystyle \frac{\text{d}w_{\bot }}{\text{d}t}}{\displaystyle \frac{\boldsymbol{w}_{\bot }}{w_{\bot }}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\dot{\unicode[STIX]{x1D717}}w_{\bot }\left(\sin \unicode[STIX]{x1D717}\,\boldsymbol{e}_{2}+\cos \unicode[STIX]{x1D717}\,\boldsymbol{e}_{1}\right)+w_{\bot }(\cos \unicode[STIX]{x1D717}\,\dot{\boldsymbol{e}}_{2}-\sin \unicode[STIX]{x1D717}\,\dot{\boldsymbol{e}}_{1}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{Z_{s}e}{m_{s}}}\left(E_{\Vert }\boldsymbol{b}+\frac{1}{c}\boldsymbol{w}\times \boldsymbol{B}\right)={\displaystyle \frac{\text{d}w_{\Vert }}{\text{d}t}}\boldsymbol{b}+w_{\Vert }\left({\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{b}}{\unicode[STIX]{x2202}t}}+\boldsymbol{w}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)+{\displaystyle \frac{\text{d}w_{\bot }}{\text{d}t}}{\displaystyle \frac{\boldsymbol{w}_{\bot }}{w_{\bot }}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\dot{\unicode[STIX]{x1D717}}w_{\bot }\left(\sin \unicode[STIX]{x1D717}\,\boldsymbol{e}_{2}+\cos \unicode[STIX]{x1D717}\,\boldsymbol{e}_{1}\right)+w_{\bot }(\cos \unicode[STIX]{x1D717}\,\dot{\boldsymbol{e}}_{2}-\sin \unicode[STIX]{x1D717}\,\dot{\boldsymbol{e}}_{1}).\end{eqnarray}$$
Taking the inner product with
![]() $\boldsymbol{w}\times \boldsymbol{b}=-w_{\bot }(\sin \unicode[STIX]{x1D717}\,\boldsymbol{e}_{2}+\cos \unicode[STIX]{x1D717}\,\boldsymbol{e}_{1})$
gives
$\boldsymbol{w}\times \boldsymbol{b}=-w_{\bot }(\sin \unicode[STIX]{x1D717}\,\boldsymbol{e}_{2}+\cos \unicode[STIX]{x1D717}\,\boldsymbol{e}_{1})$
gives
where
![]() $L_{s}$
is the magnetic shear length. Gyroaveraging gives the required answer
$L_{s}$
is the magnetic shear length. Gyroaveraging gives the required answer
In these variables, gyrophase derivatives have the property that
We will also need the leading-order gyrophase dependent pieces of the time derivatives of
![]() $\boldsymbol{R}_{s}$
and
$\boldsymbol{R}_{s}$
and
![]() $\unicode[STIX]{x1D700}_{s}$
, which are
$\unicode[STIX]{x1D700}_{s}$
, which are
and
respectively.
In these variables the ion distribution function is given by
with
![]() $\tilde{f}_{i}\sim \unicode[STIX]{x1D716}^{3/2}f_{i}$
.
$\tilde{f}_{i}\sim \unicode[STIX]{x1D716}^{3/2}f_{i}$
.
A.1 Kinetic equations
In the
![]() $(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D717},t)$
variables we can write the averaged kinetic equation as
$(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},\unicode[STIX]{x1D717},t)$
variables we can write the averaged kinetic equation as
in which the fluctuating acceleration is
In all situations, the leading-order term in this equation is the gyrophase derivative, from which we learn that the distribution functions are gyrophase independent to some order in
![]() $\unicode[STIX]{x1D716}$
. Hence, all the kinetic equations for the mean quantities in this paper are derived by gyroaveraging (A 17) and retaining the leading-order terms.
$\unicode[STIX]{x1D716}$
. Hence, all the kinetic equations for the mean quantities in this paper are derived by gyroaveraging (A 17) and retaining the leading-order terms.
We will also need an equation for the gyrophase dependence of the ion distribution function (the gyrophase dependence of the electrons is too small to matter). Writing the ion distribution function as
where all the gyrophase dependence is in
![]() $\tilde{f}_{i}$
we have
$\tilde{f}_{i}$
we have
 $$\begin{eqnarray}\displaystyle & \displaystyle \left.{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\right|_{\boldsymbol{r},w_{\Vert },w_{\bot }}=-{\displaystyle \frac{\boldsymbol{w}_{\bot }}{\unicode[STIX]{x1D6FA}_{i}}}\left.\boldsymbol{\cdot }\,{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right|_{\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s}}+{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right|_{\boldsymbol{R}_{i},\unicode[STIX]{x1D700}_{i}}+\left.{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{f}_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\right|_{\boldsymbol{R}_{i},w_{\Vert },w_{\bot }}+O(\unicode[STIX]{x1D716}^{2}f_{i}), & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \left.{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\right|_{\boldsymbol{r},w_{\Vert },w_{\bot }}=-{\displaystyle \frac{\boldsymbol{w}_{\bot }}{\unicode[STIX]{x1D6FA}_{i}}}\left.\boldsymbol{\cdot }\,{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}\right|_{\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s}}+{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\left.{\displaystyle \frac{\unicode[STIX]{x2202}f_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right|_{\boldsymbol{R}_{i},\unicode[STIX]{x1D700}_{i}}+\left.{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{f}_{i}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}\right|_{\boldsymbol{R}_{i},w_{\Vert },w_{\bot }}+O(\unicode[STIX]{x1D716}^{2}f_{i}), & \displaystyle\end{eqnarray}$$
with
In addition, using our orderings for the inter-ELM turbulence, we can write the fluctuating acceleration as
which will be used in later appendices.
Appendix B. Derivation of (2.53)
In this appendix we derive the vorticity equation to a high enough order to serve for both the ELM and inter-ELM equations. To begin our derivation we multiply the averaged kinetic equation by
![]() $m_{s}\boldsymbol{v}$
and integrate over
$m_{s}\boldsymbol{v}$
and integrate over
![]() $\boldsymbol{v}$
to obtain
$\boldsymbol{v}$
to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\mathop{\sum }_{s}m_{s}n_{s}\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\mathop{\sum }_{s}\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{1}{c}}\boldsymbol{j}\times \boldsymbol{B}+\frac{1}{4\unicode[STIX]{x03C0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}-{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}\boldsymbol{B}^{2}\unicode[STIX]{x1D644}\right\rangle _{\text{turb}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\mathop{\sum }_{s}m_{s}n_{s}\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\mathop{\sum }_{s}\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{1}{c}}\boldsymbol{j}\times \boldsymbol{B}+\frac{1}{4\unicode[STIX]{x03C0}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}-{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}\boldsymbol{B}^{2}\unicode[STIX]{x1D644}\right\rangle _{\text{turb}},\end{eqnarray}$$
where
![]() $n_{s}\boldsymbol{u}_{s}=\int \,\text{d}^{3}\boldsymbol{v}\,\boldsymbol{v}f_{s}$
. In deriving this equation, we have used quasineutrality to eliminate all terms involving electric fields and the conservation properties of the collision operator. Our next step is to write this in terms of
$n_{s}\boldsymbol{u}_{s}=\int \,\text{d}^{3}\boldsymbol{v}\,\boldsymbol{v}f_{s}$
. In deriving this equation, we have used quasineutrality to eliminate all terms involving electric fields and the conservation properties of the collision operator. Our next step is to write this in terms of
![]() $\boldsymbol{w}$
. Defining
$\boldsymbol{w}$
. Defining
we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(n_{s}m_{s}\boldsymbol{u}_{s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert s}-p_{\bot s})\boldsymbol{b}\boldsymbol{b}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}-\boldsymbol{U}_{s}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}\boldsymbol{U}_{s}\right)+n_{s}m_{s}\boldsymbol{U}_{s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(n_{s}m_{s}\boldsymbol{u}_{s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert s}-p_{\bot s})\boldsymbol{b}\boldsymbol{b}]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}-\boldsymbol{U}_{s}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}\boldsymbol{U}_{s}\right)+n_{s}m_{s}\boldsymbol{U}_{s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}},\end{eqnarray}$$
where the new viscous stress tensor is
It will be convenient to rearrange (B 3) slightly into
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(n_{s}m_{s}\boldsymbol{u}_{s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert s}-p_{\bot s})\boldsymbol{b}\boldsymbol{b}]+\boldsymbol{X}_{s}\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(n_{s}m_{s}\boldsymbol{u}_{s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\int \,\text{d}^{3}\boldsymbol{v}\,m_{s}\boldsymbol{v}\boldsymbol{v}f_{s}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert s}-p_{\bot s})\boldsymbol{b}\boldsymbol{b}]+\boldsymbol{X}_{s}\qquad \quad\end{eqnarray}$$
with the abbreviation that
We now proceed to partially derive our vorticity equation. Substituting (B 5) into (B 1) we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{s}n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert }-p_{\bot })\boldsymbol{b}\boldsymbol{b}]+\boldsymbol{X}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{1}{c}}\,\boldsymbol{j}\times \boldsymbol{B}+{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}-{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}\boldsymbol{B}^{2}\unicode[STIX]{x1D644}\right\rangle _{\text{turb}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \mathop{\sum }_{s}n_{s}m_{s}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{u}_{s}+\unicode[STIX]{x1D735}p_{\bot s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }[(p_{\Vert }-p_{\bot })\boldsymbol{b}\boldsymbol{b}]+\boldsymbol{X}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{1}{c}}\,\boldsymbol{j}\times \boldsymbol{B}+{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}-{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}\boldsymbol{B}^{2}\unicode[STIX]{x1D644}\right\rangle _{\text{turb}},\end{eqnarray}$$
again using the natural notation that
![]() $p_{\Vert }=\sum _{s}p_{\Vert s}$
, etc. Now, taking
$p_{\Vert }=\sum _{s}p_{\Vert s}$
, etc. Now, taking
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\boldsymbol{b}\times$
(B 7)
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }[\boldsymbol{b}\times$
(B 7)
![]() $/B]$
, we obtain
$/B]$
, we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{b}\times \boldsymbol{u}_{s}-\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{u}_{s}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}\left(1-4\unicode[STIX]{x03C0}\frac{p_{\Vert }-p_{\bot }}{B^{2}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left(\frac{\boldsymbol{b}}{B}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}\left(p_{\Vert }-p_{\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)\boldsymbol{b}\times \boldsymbol{u}_{s}-\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{u}_{s}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}\left(1-4\unicode[STIX]{x03C0}\frac{p_{\Vert }-p_{\bot }}{B^{2}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left(\frac{\boldsymbol{b}}{B}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}\left(p_{\Vert }-p_{\bot }\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}\right),\end{eqnarray}$$
in which we have used (B 12), (B 13) and (B 15) to rewrite the first line of the right-hand side. The unadorned vector
![]() $\boldsymbol{X}$
is given by
$\boldsymbol{X}$
is given by
We now use the result (B 19) to find
![]() $\boldsymbol{U}_{s}$
:
$\boldsymbol{U}_{s}$
:
which allows us to simplify
![]() $\boldsymbol{X}_{s}$
:
$\boldsymbol{X}_{s}$
:
with the notation
![]() $\boldsymbol{u}_{\text{d}s}=\boldsymbol{b}\times \unicode[STIX]{x1D735}p_{\bot s}/n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}$
for the diamagnetic velocity of species
$\boldsymbol{u}_{\text{d}s}=\boldsymbol{b}\times \unicode[STIX]{x1D735}p_{\bot s}/n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}$
for the diamagnetic velocity of species
![]() $s$
.
$s$
.
B.1 Manipulations leading to (B 8)
We now provide the results alluded to above. Firstly,
in which we have used quasineutrality in the form
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{j}=0$
. For our next trick, we see that
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{j}=0$
. For our next trick, we see that
Finally,
whereupon we can use
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{B}/B$
and Ampère’s law to obtain
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{b}=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\times \boldsymbol{B}/B$
and Ampère’s law to obtain
Setting
![]() $a=p_{\Vert }-p_{\bot }$
gives exactly the result needed above.
$a=p_{\Vert }-p_{\bot }$
gives exactly the result needed above.
B.2 Lowest-order flows
Let us first calculate the perpendicular velocity of a generic ion species:
We then integrate by parts in
![]() $\unicode[STIX]{x1D717}$
, using
$\unicode[STIX]{x1D717}$
, using
![]() $\boldsymbol{w}_{\bot }=\unicode[STIX]{x2202}\boldsymbol{b}\times \boldsymbol{w}/\unicode[STIX]{x2202}\unicode[STIX]{x1D717}$
, to obtain
$\boldsymbol{w}_{\bot }=\unicode[STIX]{x2202}\boldsymbol{b}\times \boldsymbol{w}/\unicode[STIX]{x2202}\unicode[STIX]{x1D717}$
, to obtain
Next we substitute from (A 20), noting that only the first term on the right-hand side of (A 20) is large enough to contribute, and find
Using the gyrotropy of
![]() $f_{s}$
and performing the gyroaverage, we obtain the final result
$f_{s}$
and performing the gyroaverage, we obtain the final result
where we have expanded the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow to lowest order and reverted to using
$\boldsymbol{E}\times \boldsymbol{B}$
flow to lowest order and reverted to using
![]() $\boldsymbol{v}$
instead of
$\boldsymbol{v}$
instead of
![]() $\boldsymbol{w}$
. Thus the perpendicular flow is simply the sum of the diamagnetic flow and the electrostatic
$\boldsymbol{w}$
. Thus the perpendicular flow is simply the sum of the diamagnetic flow and the electrostatic
![]() $\boldsymbol{E}\times \boldsymbol{B}$
flow.
$\boldsymbol{E}\times \boldsymbol{B}$
flow.
B.3 The ion stress tensor
In this section we calculate the stress tensor
![]() $\unicode[STIX]{x1D745}_{s}$
. By using the identity (A 8) in the definition (B 4), we can write
$\unicode[STIX]{x1D745}_{s}$
. By using the identity (A 8) in the definition (B 4), we can write
![]() $\unicode[STIX]{x1D745}_{s}$
as
$\unicode[STIX]{x1D745}_{s}$
as
By the same manipulations as in the previous section we can show that
Using this result, we can rewrite
![]() $\unicode[STIX]{x1D745}_{s}$
in the following way
$\unicode[STIX]{x1D745}_{s}$
in the following way
where we have abbreviated
We now proceed to the final term of (B 22). Using (A 20) we see that
The first of these terms is easily handled,
We then perform the gyroaverage, to obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D652}\boldsymbol{w}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}=-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}^{2}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{w_{\bot }^{4}}{16}}\left[\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }-\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\right]f_{s}+O(\unicode[STIX]{x1D716}^{2}p_{\bot s})\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left[\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)-\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}^{2}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{w_{\bot }^{4}}{16}}f_{s}+O(\unicode[STIX]{x1D716}^{2}p_{\bot s}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D652}\boldsymbol{w}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}=-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}^{2}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{w_{\bot }^{4}}{16}}\left[\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }-\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\right]f_{s}+O(\unicode[STIX]{x1D716}^{2}p_{\bot s})\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left[\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)\left(\boldsymbol{b}\times \unicode[STIX]{x1D735}\right)-\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}^{2}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{w_{\bot }^{4}}{16}}f_{s}+O(\unicode[STIX]{x1D716}^{2}p_{\bot s}),\end{eqnarray}$$
where the operator
![]() $(\boldsymbol{b}\times \unicode[STIX]{x1D735})(\boldsymbol{b}\times \unicode[STIX]{x1D735})$
is given by its components as
$(\boldsymbol{b}\times \unicode[STIX]{x1D735})(\boldsymbol{b}\times \unicode[STIX]{x1D735})$
is given by its components as
![]() $\unicode[STIX]{x1D716}_{ikl}\unicode[STIX]{x1D716}_{jmn}b_{k}b_{m}\unicode[STIX]{x1D735}_{l}\unicode[STIX]{x1D735}_{n}$
with
$\unicode[STIX]{x1D716}_{ikl}\unicode[STIX]{x1D716}_{jmn}b_{k}b_{m}\unicode[STIX]{x1D735}_{l}\unicode[STIX]{x1D735}_{n}$
with
![]() $\unicode[STIX]{x1D716}_{ijk}$
the Levi-Civita symbol. Writing the product
$\unicode[STIX]{x1D716}_{ijk}$
the Levi-Civita symbol. Writing the product
![]() $\unicode[STIX]{x1D716}_{ikl}\unicode[STIX]{x1D716}_{jmn}$
in terms of Kronecker deltas, we have that
$\unicode[STIX]{x1D716}_{ikl}\unicode[STIX]{x1D716}_{jmn}$
in terms of Kronecker deltas, we have that
whereupon (B 26) becomes
Moving to the second term in (B 24), and substituting from (A 6), we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle m_{s}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\qquad \quad \nonumber\\ \displaystyle & & \displaystyle \quad =\,m_{s}\int \,\text{d}^{3}\boldsymbol{w}\left\langle \unicode[STIX]{x1D652}\,\left[-\frac{m_{s}}{B}\boldsymbol{w}\times \boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{V}_{\text{D}s}+\boldsymbol{w}_{\bot }\boldsymbol{w}_{\bot }\boldsymbol{ : }\left(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\right\rangle _{\boldsymbol{r}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}},\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle m_{s}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\qquad \quad \nonumber\\ \displaystyle & & \displaystyle \quad =\,m_{s}\int \,\text{d}^{3}\boldsymbol{w}\left\langle \unicode[STIX]{x1D652}\,\left[-\frac{m_{s}}{B}\boldsymbol{w}\times \boldsymbol{b}\boldsymbol{\cdot }\boldsymbol{V}_{\text{D}s}+\boldsymbol{w}_{\bot }\boldsymbol{w}_{\bot }\boldsymbol{ : }\left(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\right\rangle _{\boldsymbol{r}}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}},\qquad \quad\end{eqnarray}$$
where we have used the fact that
![]() $(\unicode[STIX]{x1D644}-\boldsymbol{b}\boldsymbol{b})\boldsymbol{ : }(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}})$
is small. Explicitly performing the gyroaverages, the first term vanishes (gyroaverage of an odd power of
$(\unicode[STIX]{x1D644}-\boldsymbol{b}\boldsymbol{b})\boldsymbol{ : }(w_{\Vert }\unicode[STIX]{x1D735}\boldsymbol{b}+\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}})$
is small. Explicitly performing the gyroaverages, the first term vanishes (gyroaverage of an odd power of
![]() $\boldsymbol{w}_{\bot }$
) and the second term gives
$\boldsymbol{w}_{\bot }$
) and the second term gives
where the symmetric tensors
![]() $\unicode[STIX]{x1D63D}$
and
$\unicode[STIX]{x1D63D}$
and
![]() $\unicode[STIX]{x1D650}$
are given by their components
$\unicode[STIX]{x1D650}$
are given by their components
and
respectively.
Finally, the third term in (B 24) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle m_{s}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}\,{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{f}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}=-m_{s}\int \,\text{d}^{3}\boldsymbol{w}\frac{\unicode[STIX]{x1D652}}{\unicode[STIX]{x1D6FA}_{s}}\,\left[\left(\dot{\boldsymbol{R}}_{s}-\left\langle \dot{\boldsymbol{R}}_{s}\right\rangle _{\boldsymbol{R}}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+\left(\dot{\unicode[STIX]{x1D700}}_{s}-\left\langle \dot{\unicode[STIX]{x1D700}}_{s}\right\rangle _{\boldsymbol{R}}\right){\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle m_{s}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}\,{\displaystyle \frac{\unicode[STIX]{x2202}\tilde{f}_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}}=-m_{s}\int \,\text{d}^{3}\boldsymbol{w}\frac{\unicode[STIX]{x1D652}}{\unicode[STIX]{x1D6FA}_{s}}\,\left[\left(\dot{\boldsymbol{R}}_{s}-\left\langle \dot{\boldsymbol{R}}_{s}\right\rangle _{\boldsymbol{R}}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+\left(\dot{\unicode[STIX]{x1D700}}_{s}-\left\langle \dot{\unicode[STIX]{x1D700}}_{s}\right\rangle _{\boldsymbol{R}}\right){\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\,\unicode[STIX]{x1D652}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
Using the expression (A 14) for
![]() $\dot{\boldsymbol{R}}_{s}$
, we can see that the first term on the right-hand side of this equation vanishes upon gyroaveraging. For the second term, we have
$\dot{\boldsymbol{R}}_{s}$
, we can see that the first term on the right-hand side of this equation vanishes upon gyroaveraging. For the second term, we have
Whereupon we can perform the gyroaverage as above to obtain
Collecting these intermediate results, we have that
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D745}_{s} & = & \displaystyle \boldsymbol{b}\boldsymbol{h}+\boldsymbol{h}\boldsymbol{b}+\left[\unicode[STIX]{x1D644}\unicode[STIX]{x1D6FB}^{2}-2\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}w_{\bot }^{4}}{16\unicode[STIX]{x1D6FA}_{s}^{2}}}f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D63D}}{32}}\int \,\text{d}^{3}\boldsymbol{w}\frac{m_{s}^{2}w_{\bot }^{4}}{B\unicode[STIX]{x1D6FA}_{s}}w_{\Vert }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}+\unicode[STIX]{x1D650}\left[\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}^{2}w_{\bot }^{4}}{32\unicode[STIX]{x1D6FA}_{s}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\frac{1}{B}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D652}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D745}_{s} & = & \displaystyle \boldsymbol{b}\boldsymbol{h}+\boldsymbol{h}\boldsymbol{b}+\left[\unicode[STIX]{x1D644}\unicode[STIX]{x1D6FB}^{2}-2\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}w_{\bot }^{4}}{16\unicode[STIX]{x1D6FA}_{s}^{2}}}f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D63D}}{32}}\int \,\text{d}^{3}\boldsymbol{w}\frac{m_{s}^{2}w_{\bot }^{4}}{B\unicode[STIX]{x1D6FA}_{s}}w_{\Vert }{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}+\unicode[STIX]{x1D650}\left[\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}^{2}w_{\bot }^{4}}{32\unicode[STIX]{x1D6FA}_{s}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\frac{1}{B}{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D652}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
One final manipulation is to integrate by parts where possible to obtain
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D745}_{s} & = & \displaystyle \boldsymbol{b}\boldsymbol{h}+\boldsymbol{h}\boldsymbol{b}+\left[\unicode[STIX]{x1D644}\unicode[STIX]{x1D6FB}^{2}-2\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}w_{\bot }^{4}}{16\unicode[STIX]{x1D6FA}_{s}^{2}}}\,f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{\unicode[STIX]{x1D63D}}{4\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2}}w_{\bot }^{2}w_{\Vert }\,f_{s}-{\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\left\langle \int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D652}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}.\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D745}_{s} & = & \displaystyle \boldsymbol{b}\boldsymbol{h}+\boldsymbol{h}\boldsymbol{b}+\left[\unicode[STIX]{x1D644}\unicode[STIX]{x1D6FB}^{2}-2\unicode[STIX]{x1D735}_{\bot }\unicode[STIX]{x1D735}_{\bot }\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}w_{\bot }^{4}}{16\unicode[STIX]{x1D6FA}_{s}^{2}}}\,f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{\unicode[STIX]{x1D63D}}{4\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2}}w_{\bot }^{2}w_{\Vert }\,f_{s}-{\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\left\langle \int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D652}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}.\qquad\end{eqnarray}$$
B.4 The ELM vorticity equation
Let us now simplify the quantity
![]() $\boldsymbol{X}_{s}$
in the vorticity equation for the ELM ordering. Estimating the size of other terms, we see that we need the final vorticity equation correct to order
$\boldsymbol{X}_{s}$
in the vorticity equation for the ELM ordering. Estimating the size of other terms, we see that we need the final vorticity equation correct to order
![]() $O(p_{\bot }/L_{\Vert }L_{\bot }B)$
. This means we need
$O(p_{\bot }/L_{\Vert }L_{\bot }B)$
. This means we need
![]() $\boldsymbol{X}$
to
$\boldsymbol{X}$
to
![]() $O(p_{\bot }/L_{\Vert })$
.
$O(p_{\bot }/L_{\Vert })$
.
With this ordering, (B 11) becomes
Examining the form of
![]() $\unicode[STIX]{x1D745}_{s}$
, it can easily be seen that
$\unicode[STIX]{x1D745}_{s}$
, it can easily be seen that
and so the third term in (B 37) does not contribute to (B 38). Similarly terms involving
![]() $\boldsymbol{h}$
or
$\boldsymbol{h}$
or
![]() $\unicode[STIX]{x1D63D}$
can be seen to be
$\unicode[STIX]{x1D63D}$
can be seen to be
![]() $O(\sqrt{\unicode[STIX]{x1D716}}p_{\bot }/L_{\Vert })$
and so too small to be kept.
$O(\sqrt{\unicode[STIX]{x1D716}}p_{\bot }/L_{\Vert })$
and so too small to be kept.
Hence, we can substitute from (B 37) into (B 38) to obtain
 $$\begin{eqnarray}\displaystyle \boldsymbol{X}_{s} & = & \displaystyle -\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}\right)-n_{s}m_{s}u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(u_{\Vert s}\boldsymbol{b})-u_{\Vert s}\,\boldsymbol{b}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n_{s}m_{s}u_{\Vert s}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad +\,n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\left\langle \int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D652}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}+O\left(\sqrt{\unicode[STIX]{x1D716}}{\displaystyle \frac{p_{\Vert }}{L_{\Vert }}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \boldsymbol{X}_{s} & = & \displaystyle -\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}\right)-n_{s}m_{s}u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}(u_{\Vert s}\boldsymbol{b})-u_{\Vert s}\,\boldsymbol{b}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(n_{s}m_{s}u_{\Vert s}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad +\,n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}-{\displaystyle \frac{m_{s}}{\unicode[STIX]{x1D6FA}_{s}}}\left\langle \int \,\text{d}^{3}\boldsymbol{w}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D652}}{\unicode[STIX]{x2202}\boldsymbol{w}}}\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}+O\left(\sqrt{\unicode[STIX]{x1D716}}{\displaystyle \frac{p_{\Vert }}{L_{\Vert }}}\right).\end{eqnarray}$$
We now use this in the definition of
![]() $\boldsymbol{X}$
to obtain
$\boldsymbol{X}$
to obtain
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}={\displaystyle \frac{\boldsymbol{b}}{B}}\times \left[n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}\right)\right]-n_{s}m_{s}u_{\Vert s}^{2}\boldsymbol{b}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D64B}_{2}+{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right)-{\displaystyle \frac{\boldsymbol{b}}{8\unicode[STIX]{x03C0}B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}B^{2}\right\rangle _{\text{turb}}+O\left(\sqrt{\unicode[STIX]{x1D716}}{\displaystyle \frac{p_{\bot }}{L_{\Vert }B}}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}={\displaystyle \frac{\boldsymbol{b}}{B}}\times \left[n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\bot s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D650}\right)\right]-n_{s}m_{s}u_{\Vert s}^{2}\boldsymbol{b}\times \boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\unicode[STIX]{x1D64B}_{2}+{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right)-{\displaystyle \frac{\boldsymbol{b}}{8\unicode[STIX]{x03C0}B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}B^{2}\right\rangle _{\text{turb}}+O\left(\sqrt{\unicode[STIX]{x1D716}}{\displaystyle \frac{p_{\bot }}{L_{\Vert }B}}\right),\nonumber\\ \displaystyle & & \displaystyle\end{eqnarray}$$
where we have used the explicit formula for
![]() $\unicode[STIX]{x1D652}$
to evaluate the term involving the fluctuations and then, as we need to keep only the leading order, substituted
$\unicode[STIX]{x1D652}$
to evaluate the term involving the fluctuations and then, as we need to keep only the leading order, substituted
![]() $\boldsymbol{v}$
for
$\boldsymbol{v}$
for
![]() $\boldsymbol{w}$
in this expression, before using
$\boldsymbol{w}$
in this expression, before using
to write the result concisely.
Taking the divergence of this result, the final term vanishes and the terms involving the parallel velocity will cancel those on the left-hand side of (B 8). This leaves us with the expected terms involving fluctuations, and also terms involving the diamagnetic and
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocities. However, it can be shown by direct evaluation in index notation that
$\boldsymbol{E}\times \boldsymbol{B}$
velocities. However, it can be shown by direct evaluation in index notation that
Thus, these terms cancel. This important result is the expression, in our formulation, of the well-known gyro-viscous cancellation (Hazeltine & Meiss Reference Hazeltine and Meiss2003).
B.5 Turbulent contributions to the vorticity equation
Let us now massage the term involving the fluctuations. The tensor
![]() $\unicode[STIX]{x1D64B}_{2}$
is given explicitly by,
$\unicode[STIX]{x1D64B}_{2}$
is given explicitly by,
where we have used the fact that
![]() $\int \,\text{d}^{3}\boldsymbol{v}\,=\int \,\text{d}^{3}\boldsymbol{w}$
and
$\int \,\text{d}^{3}\boldsymbol{v}\,=\int \,\text{d}^{3}\boldsymbol{w}$
and
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{v}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{w}$
. Integrating by parts and using the definition of
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{v}=\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{w}$
. Integrating by parts and using the definition of
![]() $\unicode[STIX]{x1D652}$
we have
$\unicode[STIX]{x1D652}$
we have
Now, we calculate the contribution to the vorticity equation in index notation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D716}_{ijk}b_{j}\int \,\text{d}^{3}\boldsymbol{w}[\unicode[STIX]{x1D716}_{kmn}b_{n}(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot m}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{\bot m})+(l\leftrightarrow k)]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \int \,\text{d}^{3}\boldsymbol{w}[\,(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot i}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{i})\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\phantom{\int \,\text{d}^{3}\boldsymbol{w}}+\,\unicode[STIX]{x1D716}_{ijk}\unicode[STIX]{x1D716}_{lmn}b_{j}b_{n}(\unicode[STIX]{x1D6FF}a_{\bot k}w_{\bot m}+w_{\bot k}\unicode[STIX]{x1D6FF}a_{m})]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \int \,\text{d}^{3}\boldsymbol{w}[2(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot i}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{i})-(\unicode[STIX]{x1D6FF}_{il}-b_{i}b_{l})\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{w}_{\bot }]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}.\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D716}_{ijk}b_{j}\int \,\text{d}^{3}\boldsymbol{w}[\unicode[STIX]{x1D716}_{kmn}b_{n}(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot m}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{\bot m})+(l\leftrightarrow k)]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \int \,\text{d}^{3}\boldsymbol{w}[\,(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot i}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{i})\right.\nonumber\\ \displaystyle & & \displaystyle \quad \left.\phantom{\int \,\text{d}^{3}\boldsymbol{w}}+\,\unicode[STIX]{x1D716}_{ijk}\unicode[STIX]{x1D716}_{lmn}b_{j}b_{n}(\unicode[STIX]{x1D6FF}a_{\bot k}w_{\bot m}+w_{\bot k}\unicode[STIX]{x1D6FF}a_{m})]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}}{4\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \int \,\text{d}^{3}\boldsymbol{w}[2(\unicode[STIX]{x1D6FF}a_{\bot l}w_{\bot i}+w_{\bot l}\unicode[STIX]{x1D6FF}a_{i})-(\unicode[STIX]{x1D6FF}_{il}-b_{i}b_{l})\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{w}_{\bot }]\unicode[STIX]{x1D6FF}f_{s}\right\rangle _{\text{turb}}.\qquad \quad\end{eqnarray}$$
We now attack the second term in the brackets here, which contains at its core the following gyroaverage
The first identity we will need is
which can be derived from the definition of
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}$
by direct substitution. We have specialised to the ions as the electrons do not contribute to the momentum (and thus vorticity) equation. Inserting this result into our gyroaverage gives
$\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}$
by direct substitution. We have specialised to the ions as the electrons do not contribute to the momentum (and thus vorticity) equation. Inserting this result into our gyroaverage gives
Now
Thus we have
where we have defined the higher-order piece of
![]() $\unicode[STIX]{x1D6FF}f_{s}$
by
$\unicode[STIX]{x1D6FF}f_{s}$
by
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{s}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}^{(2)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}} & = & \displaystyle \left\langle {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}t}}\right\rangle _{\boldsymbol{R}}-{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}t}}-\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\left(f_{s}+\unicode[STIX]{x1D6FF}f_{s}\right)+\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\left(f_{s}+\unicode[STIX]{x1D6FF}f_{s}\right)\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & = & \displaystyle Z_{i}e{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}(\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711})+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}(\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711})\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}(f_{i}+h_{i})\nonumber\\ \displaystyle & & \displaystyle \quad +\,O(\unicode[STIX]{x1D716}^{3/2}\unicode[STIX]{x1D6FA}_{s}f_{i}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{s}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}^{(2)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D717}}} & = & \displaystyle \left\langle {\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}t}}\right\rangle _{\boldsymbol{R}}-{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}t}}-\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\left(f_{s}+\unicode[STIX]{x1D6FF}f_{s}\right)+\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\left(f_{s}+\unicode[STIX]{x1D6FF}f_{s}\right)\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & = & \displaystyle Z_{i}e{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}(\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711})+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times {\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}(\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}-\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711})\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{i}}}(f_{i}+h_{i})\nonumber\\ \displaystyle & & \displaystyle \quad +\,O(\unicode[STIX]{x1D716}^{3/2}\unicode[STIX]{x1D6FA}_{s}f_{i}),\end{eqnarray}$$
where in the second line we have specialised to the ion species. Substituting back into (B 51), we see that
Combining these results together, the leading-order part of (B 46) is given by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\mathop{\sum }_{s=i}{\displaystyle \frac{Z_{i}e}{2\unicode[STIX]{x1D6FA}_{i}}}\left\{\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{ : }\left\langle \int \,\text{d}^{3}\boldsymbol{w}\left[\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)\boldsymbol{w}_{\bot }+\boldsymbol{w}_{\bot }\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)\right]\unicode[STIX]{x1D6FF}f_{i}\right\rangle _{\text{turb}}\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D71B}\equiv \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\,-\mathop{\sum }_{s=i}{\displaystyle \frac{Z_{i}e}{2\unicode[STIX]{x1D6FA}_{i}}}\left\{\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\boldsymbol{ : }\left\langle \int \,\text{d}^{3}\boldsymbol{w}\left[\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)\boldsymbol{w}_{\bot }+\boldsymbol{w}_{\bot }\left(\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)\right]\unicode[STIX]{x1D6FF}f_{i}\right\rangle _{\text{turb}}\right\}.\end{eqnarray}$$
Finally, we show that the fluctuating Maxwell stress is negligible.
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right) & = & \displaystyle \unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D716}_{ijk}b_{j}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D6FF}B_{l}\unicode[STIX]{x1D6FF}B_{k}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{ijk}b_{j}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x1D716}_{krs}b_{r}\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{lmn}(\unicode[STIX]{x1D6FF}_{ir}\unicode[STIX]{x1D6FF}_{js}-\unicode[STIX]{x1D6FF}_{is}\unicode[STIX]{x1D6FF}_{jr})b_{j}b_{m}b_{r}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}},\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right) & = & \displaystyle \unicode[STIX]{x2202}_{i}\unicode[STIX]{x1D716}_{ijk}b_{j}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D6FF}B_{l}\unicode[STIX]{x1D6FF}B_{k}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{ijk}b_{j}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x1D716}_{krs}b_{r}\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{lmn}(\unicode[STIX]{x1D6FF}_{ir}\unicode[STIX]{x1D6FF}_{js}-\unicode[STIX]{x1D6FF}_{is}\unicode[STIX]{x1D6FF}_{jr})b_{j}b_{m}b_{r}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}},\qquad \quad\end{eqnarray}$$
where we have used the fact that terms involving
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}$
and those involving gradients of
$\unicode[STIX]{x1D6FF}\boldsymbol{B}\boldsymbol{\cdot }\boldsymbol{b}$
and those involving gradients of
![]() $\boldsymbol{b}$
are too small to contribute (these terms are
$\boldsymbol{b}$
are too small to contribute (these terms are
![]() $O(\unicode[STIX]{x1D716}^{2}p_{\bot }/L_{\bot }^{2}B)$
). Now, using the fact that
$O(\unicode[STIX]{x1D716}^{2}p_{\bot }/L_{\bot }^{2}B)$
). Now, using the fact that
![]() $b_{r}\unicode[STIX]{x2202}_{r}=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ll \unicode[STIX]{x1D735}_{\bot }$
, we have
$b_{r}\unicode[STIX]{x2202}_{r}=\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\ll \unicode[STIX]{x1D735}_{\bot }$
, we have
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right) & = & \displaystyle -\unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left(\unicode[STIX]{x2202}_{n}\left\langle \unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}-\left\langle \unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{n}\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{lmn}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x2202}_{s}{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}A_{\Vert }^{2}\right\rangle _{\text{turb}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{B}\unicode[STIX]{x1D6FF}\boldsymbol{B}\right\rangle _{\text{turb}}\right) & = & \displaystyle -\unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D716}_{lmn}b_{m}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left(\unicode[STIX]{x2202}_{n}\left\langle \unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}-\left\langle \unicode[STIX]{x1D6FF}A_{\Vert }\unicode[STIX]{x2202}_{n}\unicode[STIX]{x2202}_{s}\unicode[STIX]{x1D6FF}A_{\Vert }\right\rangle _{\text{turb}}\right)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D716}_{lmn}\unicode[STIX]{x2202}_{i}\unicode[STIX]{x2202}_{l}\left\langle \unicode[STIX]{x2202}_{n}\unicode[STIX]{x2202}_{s}{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FF}A_{\Vert }^{2}\right\rangle _{\text{turb}}=0.\end{eqnarray}$$
With these results, we see that we do indeed obtain the required vorticity equation (2.53).
B.6 The inter-ELM vorticity equation
We now need terms in the vorticity equation to
![]() $O(\unicode[STIX]{x1D716}^{3/2}p_{\bot }/L_{\bot }^{2})$
. Firstly, we note that the gyroviscous calculation, and the calculation of the fluctuating Maxwell stress are already accurate to a high enough order; we do not need to revisit them. However, we now need to go back and handle some extra terms in both
$O(\unicode[STIX]{x1D716}^{3/2}p_{\bot }/L_{\bot }^{2})$
. Firstly, we note that the gyroviscous calculation, and the calculation of the fluctuating Maxwell stress are already accurate to a high enough order; we do not need to revisit them. However, we now need to go back and handle some extra terms in both
![]() $\boldsymbol{X}_{s}$
and our formula for
$\boldsymbol{X}_{s}$
and our formula for
![]() $\unicode[STIX]{x1D745}_{s}$
. Firstly, the terms on the left-hand side of (B 8) involving
$\unicode[STIX]{x1D745}_{s}$
. Firstly, the terms on the left-hand side of (B 8) involving
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}$
are
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}$
are
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{u}_{s}\right)=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \left(u_{\Vert s}\boldsymbol{b}+\boldsymbol{u}_{\text{d}s}+\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle =\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[n_{s}m_{s}u_{\Vert s}^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{b}+n_{s}m_{s}u_{\Vert s}\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{\cdot }\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\boldsymbol{b}\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{u}_{s}\right)=\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \left(u_{\Vert s}\boldsymbol{b}+\boldsymbol{u}_{\text{d}s}+\boldsymbol{u}_{\boldsymbol{E}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle =\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[n_{s}m_{s}u_{\Vert s}^{2}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\times \boldsymbol{b}+n_{s}m_{s}u_{\Vert s}\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{\cdot }\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\boldsymbol{b}\right].\end{eqnarray}$$
We can see that, because of our ordering on
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, only the centrifugal term is large enough to matter. This will, of course, cancel with terms in
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, only the centrifugal term is large enough to matter. This will, of course, cancel with terms in
![]() $\boldsymbol{X}_{s}$
as in the previous calculation.
$\boldsymbol{X}_{s}$
as in the previous calculation.
Returning to (B 11) and retaining all terms, we see that
 $$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times (\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\,\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\text{d}s})\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D735}_{\bot }p_{\bot s}}{n_{s}m_{s}B\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}+n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\right)+{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}),\qquad \quad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times (\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\,\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\text{d}s})\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D735}_{\bot }p_{\bot s}}{n_{s}m_{s}B\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(n_{s}m_{s}u_{\Vert s}\,\boldsymbol{b}+n_{s}m_{s}\boldsymbol{u}_{\text{d}s}\right)+{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}),\qquad \quad\end{eqnarray}$$
in which we have used the definition of the diamagnetic velocity. Expanding the third and fourth terms in this expression it becomes
 $$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}\right)-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\left[{\displaystyle \frac{\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D735}_{\bot }p_{\bot s}}{n_{s}m_{s}B\unicode[STIX]{x1D6FA}_{s}}}\left[n_{s}m_{s}u_{\Vert s}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(n_{s}m_{s}u_{\Vert s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}\times \unicode[STIX]{x1D735}p_{\bot s}}{\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}\right)-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad -\,{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}\left[{\displaystyle \frac{\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{\unicode[STIX]{x1D735}_{\bot }p_{\bot s}}{n_{s}m_{s}B\unicode[STIX]{x1D6FA}_{s}}}\left[n_{s}m_{s}u_{\Vert s}\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}+\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(n_{s}m_{s}u_{\Vert s}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}\times \unicode[STIX]{x1D735}p_{\bot s}}{\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}).\end{eqnarray}$$
Eliminating terms that are smaller than
![]() $O(\unicode[STIX]{x1D716}^{3/2}p_{\bot s}/BL_{\bot }^{2})$
and collecting terms together we obtain
$O(\unicode[STIX]{x1D716}^{3/2}p_{\bot s}/BL_{\bot }^{2})$
and collecting terms together we obtain
 $$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times (\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}}\right)+{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times \boldsymbol{X}_{s} & = & \displaystyle {\displaystyle \frac{\boldsymbol{b}}{B}}\times (\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s})-{\displaystyle \frac{n_{s}m_{s}}{B}}u_{\Vert s}^{2}\boldsymbol{b}\times (\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{b})\nonumber\\ \displaystyle & & \displaystyle \quad +\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}}\right)+{\displaystyle \frac{n_{s}m_{s}}{B}}\boldsymbol{b}\times (\boldsymbol{u}_{\text{d}s}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\boldsymbol{u}_{\boldsymbol{E}}).\end{eqnarray}$$
Ultimately we must handle the remaining terms in
![]() $\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}$
. It can be shown that:
$\unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D745}_{s}$
. It can be shown that:
 $$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[{\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{h}\boldsymbol{b}+\boldsymbol{b}\boldsymbol{h})\right] & = & \displaystyle -\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[{\displaystyle \frac{1}{\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D6FB}^{2}\left({\displaystyle \frac{1}{2B^{2}}}\int \,\text{d}^{3}\boldsymbol{w}m_{s}w_{\Vert }w_{\bot }^{2}\,f_{s}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,O\left(\unicode[STIX]{x1D716}^{2}{\displaystyle \frac{p_{\bot s}}{BL_{\bot }^{2}}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[{\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }(\boldsymbol{h}\boldsymbol{b}+\boldsymbol{b}\boldsymbol{h})\right] & = & \displaystyle -\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left[{\displaystyle \frac{1}{\unicode[STIX]{x1D6FA}_{s}}}\unicode[STIX]{x1D6FB}^{2}\left({\displaystyle \frac{1}{2B^{2}}}\int \,\text{d}^{3}\boldsymbol{w}m_{s}w_{\Vert }w_{\bot }^{2}\,f_{s}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,O\left(\unicode[STIX]{x1D716}^{2}{\displaystyle \frac{p_{\bot s}}{BL_{\bot }^{2}}}\right).\end{eqnarray}$$
Similarly,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{\boldsymbol{b}}{B}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(-{\displaystyle \frac{\unicode[STIX]{x1D63D}}{4\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2}}w_{\Vert }w_{\bot }^{2}\,f_{s}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}c}{2Z_{s}e}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2B^{2}}}w_{\Vert }w_{\bot }^{2}\,f_{s}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\frac{\boldsymbol{b}}{B}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(-{\displaystyle \frac{\unicode[STIX]{x1D63D}}{4\unicode[STIX]{x1D6FA}_{s}}}\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2}}w_{\Vert }w_{\bot }^{2}\,f_{s}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{m_{s}c}{2Z_{s}e}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]\int \,\text{d}^{3}\boldsymbol{w}{\displaystyle \frac{m_{s}}{2B^{2}}}w_{\Vert }w_{\bot }^{2}\,f_{s}.\end{eqnarray}$$
Thus, the vorticity equation in the inter-ELM ordering, accurate to
![]() $O(\unicode[STIX]{x1D716}^{3/2}p_{\bot }/L_{\bot }^{2}B)$
is
$O(\unicode[STIX]{x1D716}^{3/2}p_{\bot }/L_{\bot }^{2}B)$
is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left(\frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}+\frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}\left(1-4\unicode[STIX]{x03C0}{\displaystyle \frac{p_{\Vert }-p_{\bot }}{B^{2}}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}(p_{\Vert }-p_{\bot })\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D6FB}^{2}q_{\Vert s}}{B^{2}\unicode[STIX]{x1D6FA}_{s}}}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}}[(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b})\unicode[STIX]{x1D6FB}^{2}-(\unicode[STIX]{x1D735}\boldsymbol{b})\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}]q_{\Vert s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left(\frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}+\frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}\right)\right\}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}\left(1-4\unicode[STIX]{x03C0}{\displaystyle \frac{p_{\Vert }-p_{\bot }}{B^{2}}}\right)-p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)-{\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}(p_{\Vert }-p_{\bot })\right]\nonumber\\ \displaystyle & & \displaystyle \quad -\,\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D6FB}^{2}q_{\Vert s}}{B^{2}\unicode[STIX]{x1D6FA}_{s}}}\right)+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad +\,{\displaystyle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}}[(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b})\unicode[STIX]{x1D6FB}^{2}-(\unicode[STIX]{x1D735}\boldsymbol{b})\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}]q_{\Vert s}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{\boldsymbol{b}}{B}}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right),\end{eqnarray}$$
in which we have abbreviated
We postpone the flux-surface averaging of this equation to appendix C.
B.7 Gyroaverages
In the previous section we needed to gyroaverage terms like
![]() $\unicode[STIX]{x1D652}\boldsymbol{w}\boldsymbol{w}$
. These all stem from the following identity
$\unicode[STIX]{x1D652}\boldsymbol{w}\boldsymbol{w}$
. These all stem from the following identity
where
with
![]() $\unicode[STIX]{x1D6FF}$
the usual Kronecker delta. The tensor structure of the right-hand side of (B 66) follows from the absence of a preferred perpendicular direction. The coefficient in front can be calculated by picking a particular component and using e.g.
$\unicode[STIX]{x1D6FF}$
the usual Kronecker delta. The tensor structure of the right-hand side of (B 66) follows from the absence of a preferred perpendicular direction. The coefficient in front can be calculated by picking a particular component and using e.g.
![]() $(\cos ^{4}\unicode[STIX]{x1D717})=3/8$
. We can then perform gyroaverages like
$(\cos ^{4}\unicode[STIX]{x1D717})=3/8$
. We can then perform gyroaverages like
Appendix C. Flux-surface-averaged vorticity
Here we take the flux-surface average of the slow time scale vorticity equation (B 64) to obtain (3.21). The usual expressions for the flux-surface average are needed (see Dhaeseleer et al. (Reference Dhaeseleer, Hitchon, Callen and Shohet1991)), namely
where
![]() $g$
is an arbitrary function,
$g$
is an arbitrary function,
![]() $V^{\prime }$
is the area of the flux surface in question and
$V^{\prime }$
is the area of the flux surface in question and
![]() $\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},\ell$
are a set of Clebsch coordinates for the field
$\unicode[STIX]{x1D713},\unicode[STIX]{x1D6FC},\ell$
are a set of Clebsch coordinates for the field
![]() $\boldsymbol{B}$
, and
$\boldsymbol{B}$
, and
with
![]() $\boldsymbol{Y}$
an arbitrary vector field. With these identities, we see immediately that
$\boldsymbol{Y}$
an arbitrary vector field. With these identities, we see immediately that
and
 $$\begin{eqnarray}\displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\unicode[STIX]{x1D735}\times \boldsymbol{b}\right)\right\rangle _{\unicode[STIX]{x1D713}} & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\times \unicode[STIX]{x1D735}\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{1}{V^{\prime }}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}V^{\prime }\oint \text{d}\ell \text{d}\unicode[STIX]{x1D6FC}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\right),\nonumber\\ \displaystyle & = & \displaystyle 0,\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\unicode[STIX]{x1D735}\times \boldsymbol{b}\right)\right\rangle _{\unicode[STIX]{x1D713}} & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\times \unicode[STIX]{x1D735}\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & = & \displaystyle {\displaystyle \frac{1}{V^{\prime }}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}V^{\prime }\oint \text{d}\ell \text{d}\unicode[STIX]{x1D6FC}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FC}}}\left({\displaystyle \frac{p_{\Vert }-p_{\bot }}{B}}\right),\nonumber\\ \displaystyle & = & \displaystyle 0,\end{eqnarray}$$
where in both we have used only the properties of the flux surfaces, including
![]() $\unicode[STIX]{x1D6FC}$
-periodicity, but not used any ordering assumptions. These are identities that hold to all orders in
$\unicode[STIX]{x1D6FC}$
-periodicity, but not used any ordering assumptions. These are identities that hold to all orders in
![]() $\unicode[STIX]{x1D716}$
.
$\unicode[STIX]{x1D716}$
.
Finally we tackle the term
To analyse this term we need the following expression for the perpendicular current, derived from the exact momentum equation under the inter-ELM orderings
which can be trivially rewritten as
Returning to (C 5) we use the identity
which follows from Ampère’s law to obtain
 $$\begin{eqnarray}\displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)\right)\right\rangle _{\unicode[STIX]{x1D713}} & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[p_{\bot }\left({\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}+{\displaystyle \frac{\boldsymbol{b}\times \unicode[STIX]{x1D735}B}{B^{2}}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{4\unicode[STIX]{x03C0}}{c}}p_{\bot }\,\boldsymbol{j}\right)\right\rangle _{\unicode[STIX]{x1D713}},\qquad\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(p_{\bot }\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)\right)\right\rangle _{\unicode[STIX]{x1D713}} & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[p_{\bot }\left({\displaystyle \frac{\unicode[STIX]{x1D735}\times \boldsymbol{b}}{B}}+{\displaystyle \frac{\boldsymbol{b}\times \unicode[STIX]{x1D735}B}{B^{2}}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & = & \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left({\displaystyle \frac{4\unicode[STIX]{x03C0}}{c}}p_{\bot }\,\boldsymbol{j}\right)\right\rangle _{\unicode[STIX]{x1D713}},\qquad\end{eqnarray}$$
where we have used the same results that lead to (C 4) to eliminate terms containing
![]() $\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }(p_{\bot }\unicode[STIX]{x1D735}\times \boldsymbol{b}/B)\right\rangle _{\unicode[STIX]{x1D713}}$
.
$\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }(p_{\bot }\unicode[STIX]{x1D735}\times \boldsymbol{b}/B)\right\rangle _{\unicode[STIX]{x1D713}}$
.
Now, substituting (C 7) into this result, we immediately obtain
where we retain the
![]() $j_{\Vert }$
term because of our ordering for the shear length as
$j_{\Vert }$
term because of our ordering for the shear length as
![]() $\sqrt{L_{\bot }L_{\Vert }}$
. However, from our solution (2.58) for the large part of
$\sqrt{L_{\bot }L_{\Vert }}$
. However, from our solution (2.58) for the large part of
![]() $j_{\Vert }$
, we see that this entire expression becomes
$j_{\Vert }$
, we see that this entire expression becomes
and so the entire term is small.
Using these identities, the flux-surface average of (B 64) is
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]q_{\Vert s}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\boldsymbol{b}}{B}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\{\mathop{\sum }_{s}{\displaystyle \frac{n_{s}m_{s}}{B}}\left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+u_{\Vert s}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right]\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{\bot s}}{n_{s}m_{s}\unicode[STIX]{x1D6FA}_{s}}}+{\displaystyle \frac{c\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}}{B}}\right)\right\}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left(\frac{u_{\Vert s}\unicode[STIX]{x1D735}p_{\bot s}}{B\unicode[STIX]{x1D6FA}_{s}}\right)\right]\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \frac{1}{2B\unicode[STIX]{x1D6FA}_{s}}\left[\left(\unicode[STIX]{x1D735}\boldsymbol{\cdot }\boldsymbol{b}\right)\unicode[STIX]{x1D6FB}^{2}-\left(\unicode[STIX]{x1D735}\boldsymbol{b}\right)\boldsymbol{ : }\unicode[STIX]{x1D735}\unicode[STIX]{x1D735}\right]q_{\Vert s}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(\frac{\boldsymbol{b}}{B}\times \unicode[STIX]{x1D735}\boldsymbol{\cdot }\unicode[STIX]{x1D64B}_{2}\right)\right\rangle _{\unicode[STIX]{x1D713}},\end{eqnarray}$$
again, with the abbreviation for
![]() $q_{\Vert s}$
.
$q_{\Vert s}$
.
Appendix D. Derivation of the ballooning equation
In this appendix we demonstrate that our equations for ELM dynamics reduce in the appropriate limit to the ballooning equation of Tang, Connor & Hastie (Reference Tang, Connor and Hastie1980). The equations that we will linearise are (2.45) and (2.49) for the distribution functions, along with (2.47) and (2.53). For the background magnetic field, we will assume that it has topologically toroidal flux surfaces labelled by
![]() $\unicode[STIX]{x1D713}$
– the entire equilibrium field is contained in
$\unicode[STIX]{x1D713}$
– the entire equilibrium field is contained in
![]() $\boldsymbol{B}_{0}$
, there is no equilibrium
$\boldsymbol{B}_{0}$
, there is no equilibrium
![]() $A_{\Vert }$
. We will linearise around Maxwellian equilibria for both ions and electrons, with the density and temperature of the equilibria being flux functions. Consistently, we will assume that there is no equilibrium
$A_{\Vert }$
. We will linearise around Maxwellian equilibria for both ions and electrons, with the density and temperature of the equilibria being flux functions. Consistently, we will assume that there is no equilibrium
![]() $\unicode[STIX]{x1D711}$
.
$\unicode[STIX]{x1D711}$
.
We chose a form for our fluctuating quantities that parallels that in Tang et al. (Reference Tang, Connor and Hastie1980), but simplifies our notation. We will assume we are linearising in a local flux tube (Beer et al.
Reference Beer, Cowley and Hammett1995) and so every fluctuating quantity can be expressed in a Fourier series perpendicular to the field line, with a wave vector
![]() $\boldsymbol{k}_{\bot }$
. The wave vector is assumed to be large so that
$\boldsymbol{k}_{\bot }$
. The wave vector is assumed to be large so that
![]() $k_{\bot }L_{\bot }\gg 1$
, and we really are looking at a local perturbation. This is appropriate for a ballooning mode as we know that the most unstable mode occurs for
$k_{\bot }L_{\bot }\gg 1$
, and we really are looking at a local perturbation. This is appropriate for a ballooning mode as we know that the most unstable mode occurs for
![]() $n\rightarrow \infty$
, where
$n\rightarrow \infty$
, where
![]() $n$
is the toroidal mode number. Naturally, we assume exponential time dependence with frequency
$n$
is the toroidal mode number. Naturally, we assume exponential time dependence with frequency
![]() $\unicode[STIX]{x1D714}$
. We also define the following auxiliary frequencies to parallel the definitions in Tang et al. (Reference Tang, Connor and Hastie1980):
$\unicode[STIX]{x1D714}$
. We also define the following auxiliary frequencies to parallel the definitions in Tang et al. (Reference Tang, Connor and Hastie1980):
with
![]() $\unicode[STIX]{x1D702}_{s}$
,
$\unicode[STIX]{x1D702}_{s}$
,
![]() $\unicode[STIX]{x1D714}_{\ast p}$
,
$\unicode[STIX]{x1D714}_{\ast p}$
,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D705}}$
and
![]() $\unicode[STIX]{x1D714}_{B}$
defined exactly as in Tang et al. (Reference Tang, Connor and Hastie1980).
$\unicode[STIX]{x1D714}_{B}$
defined exactly as in Tang et al. (Reference Tang, Connor and Hastie1980).
Let us start by linearising and solving the ion kinetic equation (2.49) to obtain:
Hence, the perturbed ion pressure is isotropic and given by
We now linearise the electron kinetic equation (2.45), resulting in
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}f_{e}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{e}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}+{\displaystyle \frac{\text{i}c}{B}}\boldsymbol{b}\times \boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{0e}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}-ew_{\Vert }\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}+{\displaystyle \frac{1}{c}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right){\displaystyle \frac{f_{0e}}{T_{e}}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,w_{\Vert }\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}A_{\Vert }\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{0e}=C_{L}\left[\unicode[STIX]{x1D6FF}f_{e}\right],\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle -\text{i}\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FF}f_{e}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{e}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}+{\displaystyle \frac{\text{i}c}{B}}\boldsymbol{b}\times \boldsymbol{k}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{0e}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}-ew_{\Vert }\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}+{\displaystyle \frac{1}{c}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right){\displaystyle \frac{f_{0e}}{T_{e}}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,w_{\Vert }\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}A_{\Vert }\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{0e}=C_{L}\left[\unicode[STIX]{x1D6FF}f_{e}\right],\end{eqnarray}$$
where
![]() $C_{L}\left[\cdot \right]$
is the collision operator linearised about the Maxwellian equilibria. To solve this equation we need to do two things. Firstly, as is usual in linear calculations we introduce a new field
$C_{L}\left[\cdot \right]$
is the collision operator linearised about the Maxwellian equilibria. To solve this equation we need to do two things. Firstly, as is usual in linear calculations we introduce a new field
![]() $\unicode[STIX]{x1D709}$
defined by
$\unicode[STIX]{x1D709}$
defined by
Note, this representation is not in general possible, but because we are dealing with perturbations that have non-zero
![]() $n$
, neither
$n$
, neither
![]() $\unicode[STIX]{x1D6FF}A_{\Vert }$
nor
$\unicode[STIX]{x1D6FF}A_{\Vert }$
nor
![]() $\unicode[STIX]{x1D709}$
can have non-zero toroidal averages, and so this representation is both unique and well defined. Secondly, in order to make contact with equation (3.40) of Tang et al. (Reference Tang, Connor and Hastie1980), we will need to assume that the electron transit and frequencies are large compared to the frequencies of interest, and to self-consistently neglect trapped-particle effects we take
$\unicode[STIX]{x1D709}$
can have non-zero toroidal averages, and so this representation is both unique and well defined. Secondly, in order to make contact with equation (3.40) of Tang et al. (Reference Tang, Connor and Hastie1980), we will need to assume that the electron transit and frequencies are large compared to the frequencies of interest, and to self-consistently neglect trapped-particle effects we take
![]() $\unicode[STIX]{x1D708}_{ee}\sim v_{\text{th}_{e}}/L_{\Vert }\gg \unicode[STIX]{x1D714}$
. Using this subsidiary ordering, we can immediately solve (D 5) to find
$\unicode[STIX]{x1D708}_{ee}\sim v_{\text{th}_{e}}/L_{\Vert }\gg \unicode[STIX]{x1D714}$
. Using this subsidiary ordering, we can immediately solve (D 5) to find
Unfortunately, this solution satisfies the linearisation of (2.47) identically. Thus, we need to go to the next order in
![]() $\unicode[STIX]{x1D714}\left/k_{\Vert }v_{\text{th}_{e}}\right.$
to obtain a relationship between
$\unicode[STIX]{x1D714}\left/k_{\Vert }v_{\text{th}_{e}}\right.$
to obtain a relationship between
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D709}$
. This is most rapidly done by simply integrating (D 5) over all velocities and using the fact that any parallel velocity in
$\unicode[STIX]{x1D709}$
. This is most rapidly done by simply integrating (D 5) over all velocities and using the fact that any parallel velocity in
![]() $\unicode[STIX]{x1D6FF}f_{e}$
must vanish:
$\unicode[STIX]{x1D6FF}f_{e}$
must vanish:
Using the lowest-order solution for
![]() $\unicode[STIX]{x1D6FF}n_{e}$
above, we obtain
$\unicode[STIX]{x1D6FF}n_{e}$
above, we obtain
Thus,
This is just the usual condition of
![]() $\unicode[STIX]{x1D6FF}E_{\Vert }=0$
, which always obtains when the electron diamagnetic corrections to Ohm’s law can be neglected due to rapid electron motion.
$\unicode[STIX]{x1D6FF}E_{\Vert }=0$
, which always obtains when the electron diamagnetic corrections to Ohm’s law can be neglected due to rapid electron motion.
Turning now to the vorticity equation, we can drop all terms involving pressure anisotropy, and thus we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[{\displaystyle \frac{n_{i}m_{i}}{B}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}p_{i}}{n_{i}m_{i}\unicode[STIX]{x1D6FA}_{i}}+\frac{c}{B}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)+{\displaystyle \frac{cn_{i}m_{i}}{B^{2}}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{i}}{n_{i}m_{i}\unicode[STIX]{x1D6FA}_{i}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}-(\unicode[STIX]{x1D6FF}p_{i}+\unicode[STIX]{x1D6FF}p_{e})\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)\right].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[{\displaystyle \frac{n_{i}m_{i}}{B}}{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}\left(\frac{\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}p_{i}}{n_{i}m_{i}\unicode[STIX]{x1D6FA}_{i}}+\frac{c}{B}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right)+{\displaystyle \frac{cn_{i}m_{i}}{B^{2}}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{\unicode[STIX]{x1D735}p_{i}}{n_{i}m_{i}\unicode[STIX]{x1D6FA}_{i}}}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left[-{\displaystyle \frac{j_{\Vert }\boldsymbol{b}}{c}}-(\unicode[STIX]{x1D6FF}p_{i}+\unicode[STIX]{x1D6FF}p_{e})\unicode[STIX]{x1D735}\times \left({\displaystyle \frac{\boldsymbol{b}}{B}}\right)\right].\end{eqnarray}$$
Now, for consistency with the Tang et al. (Reference Tang, Connor and Hastie1980) approach, we will furthermore assume
![]() $\unicode[STIX]{x1D70C}_{i}^{2}/L_{n}L_{T}\ll \unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{i}$
which allows us to drop the final term on the left-hand side of (D 11). This is in fact a consequence of our local assumption – if
$\unicode[STIX]{x1D70C}_{i}^{2}/L_{n}L_{T}\ll \unicode[STIX]{x1D714}/\unicode[STIX]{x1D6FA}_{i}$
which allows us to drop the final term on the left-hand side of (D 11). This is in fact a consequence of our local assumption – if
![]() $\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast }$
then
$\unicode[STIX]{x1D714}\sim \unicode[STIX]{x1D714}_{\ast }$
then
We will also lean on the local approximation on the right-hand side of (D 11) and assume that
![]() $k_{\bot }L_{s}\ll 1$
, where
$k_{\bot }L_{s}\ll 1$
, where
![]() $L_{s}$
is the shear length; thus eliminating the kink drive (i.e.
$L_{s}$
is the shear length; thus eliminating the kink drive (i.e.
![]() $\unicode[STIX]{x1D6FF}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}j_{\Vert 0}$
) from (D 11).
$\unicode[STIX]{x1D6FF}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}j_{\Vert 0}$
) from (D 11).
With these approximations we obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{i\unicode[STIX]{x1D714}n_{i}T_{i}}{B\unicode[STIX]{x1D6FA}_{i}}}k_{\bot }^{2}\left[1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}}\left(1+\unicode[STIX]{x1D702}_{i}\right)\right]{\displaystyle \frac{Z_{i}e\unicode[STIX]{x1D709}}{T_{i}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{k_{\bot }^{2}ci}{\unicode[STIX]{x1D714}B}}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}\right)-i\frac{m_{i}n_{i}\unicode[STIX]{x1D6FA}_{i}}{B}\left(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D73F}}+{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{i}}{2}}\unicode[STIX]{x1D714}_{\ast p}\right){\displaystyle \frac{\unicode[STIX]{x1D714}_{\ast p}}{\unicode[STIX]{x1D714}}}{\displaystyle \frac{Z_{i}e\unicode[STIX]{x1D709}}{T_{i}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{i\unicode[STIX]{x1D714}n_{i}T_{i}}{B\unicode[STIX]{x1D6FA}_{i}}}k_{\bot }^{2}\left[1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\ast i}}{\unicode[STIX]{x1D714}}}\left(1+\unicode[STIX]{x1D702}_{i}\right)\right]{\displaystyle \frac{Z_{i}e\unicode[STIX]{x1D709}}{T_{i}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,-{\displaystyle \frac{1}{4\unicode[STIX]{x03C0}}}\boldsymbol{B}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\left({\displaystyle \frac{k_{\bot }^{2}ci}{\unicode[STIX]{x1D714}B}}\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D709}\right)-i\frac{m_{i}n_{i}\unicode[STIX]{x1D6FA}_{i}}{B}\left(2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D73F}}+{\displaystyle \frac{\unicode[STIX]{x1D6FD}_{i}}{2}}\unicode[STIX]{x1D714}_{\ast p}\right){\displaystyle \frac{\unicode[STIX]{x1D714}_{\ast p}}{\unicode[STIX]{x1D714}}}{\displaystyle \frac{Z_{i}e\unicode[STIX]{x1D709}}{T_{i}}},\end{eqnarray}$$
where we have used
Rearranging (D 13) and multiplying by
![]() $4\unicode[STIX]{x03C0}T_{i}\unicode[STIX]{x1D714}/iZ_{i}e\unicode[STIX]{x1D6FA}_{i}B$
, we obtain
$4\unicode[STIX]{x03C0}T_{i}\unicode[STIX]{x1D714}/iZ_{i}e\unicode[STIX]{x1D6FA}_{i}B$
, we obtain
where we have used the fact that
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T_{i}=0$
and introduced the notation
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}T_{i}=0$
and introduced the notation
![]() $b=k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$
.
$b=k_{\bot }^{2}\unicode[STIX]{x1D70C}_{i}^{2}/2$
.
Inserting explicit geometric expressions for
![]() $\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, and dropping the
$\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}$
, and dropping the
![]() $\unicode[STIX]{x1D6FD}_{i}$
term, (D 15) matches the first line of (3.40) of Tang et al. (Reference Tang, Connor and Hastie1980). The second line of the ballooning equation in Tang et al. (Reference Tang, Connor and Hastie1980) is small in our ordering, because
$\unicode[STIX]{x1D6FD}_{i}$
term, (D 15) matches the first line of (3.40) of Tang et al. (Reference Tang, Connor and Hastie1980). The second line of the ballooning equation in Tang et al. (Reference Tang, Connor and Hastie1980) is small in our ordering, because
![]() $\unicode[STIX]{x1D714}_{\ast }/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D73F}}\sim L_{n}/R\ll 1$
. Taking the JET-ILW pedestals from Hatch et al. (Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017) as typical, then
$\unicode[STIX]{x1D714}_{\ast }/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D73F}}\sim L_{n}/R\ll 1$
. Taking the JET-ILW pedestals from Hatch et al. (Reference Hatch, Kotschenreuther, Mahajan, Valanju and Liu2017) as typical, then
![]() $R/L_{n}\gtrsim 50$
in the pedestal region.
$R/L_{n}\gtrsim 50$
in the pedestal region.
Hence we see that both formulations capture the key physics of ballooning modes, with our model retaining more electron and finite-
![]() $\unicode[STIX]{x1D6FD}$
physics, and the model of Tang et al. (Reference Tang, Connor and Hastie1980) retaining plasma compressibility effects (the final term in 3.6 and 3.40 of that paper).
$\unicode[STIX]{x1D6FD}$
physics, and the model of Tang et al. (Reference Tang, Connor and Hastie1980) retaining plasma compressibility effects (the final term in 3.6 and 3.40 of that paper).
Appendix E. Derivations for the inter-ELM equations
In this appendix, we perform the derivations required for the inter-ELM equations.
E.1 Electron behaviour on the slow time scale
In this section we discuss the possible solutions to the lowest-order electron kinetic equation, under the inter-ELM orderings. Taking (2.25) for the electrons, and applying the inter-ELM orderings, we see that the largest terms are those involving electron velocities:
We multiply this by
![]() $1+\ln f_{e}$
, and integrate over all velocities to obtain
$1+\ln f_{e}$
, and integrate over all velocities to obtain
where we use the fact that
![]() $f_{e}\rightarrow 0$
implies
$f_{e}\rightarrow 0$
implies
![]() $f_{e}\ln f_{e}\rightarrow 0$
at high energies. We will now assume that the magnetic field has good flux surfaces, at least to some approximation. Then, averaging over these surfaces, and applying the
$f_{e}\ln f_{e}\rightarrow 0$
at high energies. We will now assume that the magnetic field has good flux surfaces, at least to some approximation. Then, averaging over these surfaces, and applying the
![]() $H$
-theorem for the nonlinear collision operator, we obtain Maxwell–Boltzmann electrons
$H$
-theorem for the nonlinear collision operator, we obtain Maxwell–Boltzmann electrons
where
![]() $N_{e}$
and
$N_{e}$
and
![]() $T_{e}$
are flux functions. The parameter
$T_{e}$
are flux functions. The parameter
![]() $N_{e}$
is related to the electron density
$N_{e}$
is related to the electron density
![]() $n_{e}$
by
$n_{e}$
by
We can rewrite this equation as
Note that because the induced parallel electric field is small compared to the electrostatic field there is a field-line preserving flow (Newcomb Reference Newcomb1958; Abel & Cowley Reference Abel and Cowley2013). Thus, the assumption of good magnetic surfaces is consistent – if we assume that they exist initially for some time then they will be preserved by this flow.
Going to the next order in
![]() $\sqrt{\unicode[STIX]{x1D716}}$
, we expand
$\sqrt{\unicode[STIX]{x1D716}}$
, we expand
![]() $f_{e}=f_{e}^{(0)}+f_{e}^{(1)}+\cdots \,$
where
$f_{e}=f_{e}^{(0)}+f_{e}^{(1)}+\cdots \,$
where
![]() $f_{e}^{(1)}\sim \sqrt{\unicode[STIX]{x1D716}}f_{e}^{(0)}$
and so forth. Using this expansion, we obtain the kinetic equation
$f_{e}^{(1)}\sim \sqrt{\unicode[STIX]{x1D716}}f_{e}^{(0)}$
and so forth. Using this expansion, we obtain the kinetic equation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right)f_{e}^{(0)}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{e}^{(1)}+ew_{\Vert }\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}^{(1)}+{\displaystyle \frac{\unicode[STIX]{x2202}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right){\displaystyle \frac{\unicode[STIX]{x2202}f_{e}^{(0)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{e}}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,ew_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}{\displaystyle \frac{\unicode[STIX]{x2202}f_{e}^{(1)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{e}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{e}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}\right\rangle _{\boldsymbol{R}}=C_{L}\left[f_{e}^{(1)}\right]+S_{e}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{e}}}\right)f_{e}^{(0)}+w_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{e}^{(1)}+ew_{\Vert }\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}^{(1)}+{\displaystyle \frac{\unicode[STIX]{x2202}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right){\displaystyle \frac{\unicode[STIX]{x2202}f_{e}^{(0)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{e}}}\nonumber\\ \displaystyle & & \displaystyle \quad +\,ew_{\Vert }\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}{\displaystyle \frac{\unicode[STIX]{x2202}f_{e}^{(1)}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+\left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{e}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{e}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}\right\rangle _{\boldsymbol{R}}=C_{L}\left[f_{e}^{(1)}\right]+S_{e}.\end{eqnarray}$$
Integrating this over all velocities we obtain
where we have used (E 23) for the fluctuations, and introduced
because there is no electron parallel velocity in
![]() $f_{e}^{(0)}$
.
$f_{e}^{(0)}$
.
If we multiply (E 6) by
![]() $(\unicode[STIX]{x1D700}_{e}/T_{e}-3/2)$
and integrate over all velocities we find that
$(\unicode[STIX]{x1D700}_{e}/T_{e}-3/2)$
and integrate over all velocities we find that
 $$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{3}{2}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left({\displaystyle \frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}}-{\displaystyle \frac{3}{2}}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle =\,en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}+\left\langle e\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}+{\displaystyle \frac{1}{c}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right)\unicode[STIX]{x1D6FF}u_{\Vert e}\right\rangle _{\text{turb}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(q_{\Vert e}^{(1)}\boldsymbol{b}\right)+S_{e}^{(E)},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle & & \displaystyle {\displaystyle \frac{3}{2}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}+\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left({\displaystyle \frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}}-{\displaystyle \frac{3}{2}}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\nonumber\\ \displaystyle & & \displaystyle =\,en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}+\left\langle e\left(\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}+{\displaystyle \frac{1}{c}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}A_{\Vert }}{\unicode[STIX]{x2202}t}}\right)\unicode[STIX]{x1D6FF}u_{\Vert e}\right\rangle _{\text{turb}}-\unicode[STIX]{x1D735}\boldsymbol{\cdot }\left(q_{\Vert e}^{(1)}\boldsymbol{b}\right)+S_{e}^{(E)},\end{eqnarray}$$
where again we have used (E 23) for the fluctuations, and
![]() $q_{\Vert e}^{(1)}$
is a moment of
$q_{\Vert e}^{(1)}$
is a moment of
![]() $f_{e}^{(1)}$
which is not solved for. As
$f_{e}^{(1)}$
which is not solved for. As
![]() $T_{e}$
is a flux function, we average this equation over the flux surfaces to finally obtain
$T_{e}$
is a flux function, we average this equation over the flux surfaces to finally obtain
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{3}{2}}\left\langle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left({\displaystyle \frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}}-{\displaystyle \frac{3}{2}}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}\right\rangle _{\unicode[STIX]{x1D713}}-\left\langle \left\langle e\unicode[STIX]{x1D6FF}E_{\Vert }\unicode[STIX]{x1D6FF}u_{\Vert e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle S_{e}^{(E)}\right\rangle _{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{3}{2}}\left\langle \left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\right)n_{e}T_{e}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle \unicode[STIX]{x1D735}\boldsymbol{\cdot }\left\langle \int \,\text{d}^{3}\boldsymbol{v}\,\left({\displaystyle \frac{\unicode[STIX]{x1D700}_{e}}{T_{e}}}-{\displaystyle \frac{3}{2}}\right)\left\langle \boldsymbol{V}_{\unicode[STIX]{x1D712}}\right\rangle _{\boldsymbol{R}}\unicode[STIX]{x1D6FF}f_{e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle en_{e}u_{\Vert e}\,\boldsymbol{b}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D711}\right\rangle _{\unicode[STIX]{x1D713}}-\left\langle \left\langle e\unicode[STIX]{x1D6FF}E_{\Vert }\unicode[STIX]{x1D6FF}u_{\Vert e}\right\rangle _{\text{turb}}\right\rangle _{\unicode[STIX]{x1D713}}+\left\langle S_{e}^{(E)}\right\rangle _{\unicode[STIX]{x1D713}}.\end{eqnarray}$$
E.2 Pedestal gyrokinetic turbulence
In this section, we derive the equations governing the turbulence in the pedestal. To obtain the equations for the inter-ELM turbulence, we take the fluctuating part of the fundamental kinetic equation, written in Catto-transformed variables
The leading order of this equation is
whose solution can be written as
where we have split out part of the gyrophase-independent piece to more closely mirror other derivations.
Substituting this back into (E 11) and gyroaveraging gives
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\left(w_{\Vert }\boldsymbol{b}(\boldsymbol{R}_{s})+\boldsymbol{u}_{\boldsymbol{E}}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}\right]h_{s}+\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,Z_{s}e{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}\right)\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}-{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle C_{L}\left[h_{s}\right]\right\rangle _{\boldsymbol{R}}+O(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FA}_{s}h_{s}),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\left(w_{\Vert }\boldsymbol{b}(\boldsymbol{R}_{s})+\boldsymbol{u}_{\boldsymbol{E}}\right)\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}\right]h_{s}+\left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D6FF}f_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,Z_{s}e{\displaystyle \frac{\unicode[STIX]{x2202}f_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}\left({\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}t}}+\boldsymbol{u}_{\boldsymbol{E}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}\right)\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}-{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}f_{s}\nonumber\\ \displaystyle & & \displaystyle \quad +\,\left\langle C_{L}\left[h_{s}\right]\right\rangle _{\boldsymbol{R}}+O(\unicode[STIX]{x1D716}\unicode[STIX]{x1D6FA}_{s}h_{s}),\end{eqnarray}$$
where we have used explicit forms for the time derivatives, written
![]() $f_{s}=f_{s}(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},t)$
and used the chain rule. By exactly the same manipulations as we use in the next section for the nonlinear term in the transport equations, we can show that
$f_{s}=f_{s}(\boldsymbol{R}_{s},\unicode[STIX]{x1D700}_{s},\unicode[STIX]{x1D707}_{s},t)$
and used the chain rule. By exactly the same manipulations as we use in the next section for the nonlinear term in the transport equations, we can show that
All that remains to derive the gyrokinetic equations in § 3.3 is to specialise the above results to electrons and ions. The field equations follow immediately from the fluctuating parts of quasineutrality and Ampère’s law.
E.3 Turbulent transport in the pedestal
To derive the terms involving the fluctuations in the inter-ELM equations, we need the following results. Firstly, the nonlinear term in the averaged kinetic equation is
and so in order to perform the gyroaverage, we need to convert the velocity derivative into a derivative of the gyrokinetic variables. We require this term up only to
![]() $O(v_{\text{th}_{i}}f_{s}/L_{\Vert })$
and will systematically neglect any higher-order terms. We first do this for the non-adiabatic part of the distribution function:
$O(v_{\text{th}_{i}}f_{s}/L_{\Vert })$
and will systematically neglect any higher-order terms. We first do this for the non-adiabatic part of the distribution function:
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+m_{s}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{v}{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+{\displaystyle \frac{m_{s}}{B}}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{v}_{\bot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right\rangle _{\boldsymbol{R}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\right\rangle _{\text{turb}}\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,\left\langle \left\langle \unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}{\unicode[STIX]{x2202}\boldsymbol{v}}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}+m_{s}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{v}{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D700}_{s}}}+{\displaystyle \frac{m_{s}}{B}}\unicode[STIX]{x1D6FF}\boldsymbol{a}_{s}\boldsymbol{\cdot }\boldsymbol{v}_{\bot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D707}_{s}}}\right\rangle _{\boldsymbol{R}}\right\rangle _{\text{turb}}.\end{eqnarray}$$
Using the explicit form of the fluctuating acceleration, we see that
and
where we have used
![]() $\left\langle \boldsymbol{v}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}G\right\rangle _{\boldsymbol{R}}=0$
for any fluctuating field
$\left\langle \boldsymbol{v}_{\bot }\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}G\right\rangle _{\boldsymbol{R}}=0$
for any fluctuating field
![]() $\unicode[STIX]{x1D6FF}G$
that is independent of gyrophase at fixed
$\unicode[STIX]{x1D6FF}G$
that is independent of gyrophase at fixed
![]() $\boldsymbol{r}$
(see (A.4) of (Abel et al.
Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013)).
$\boldsymbol{r}$
(see (A.4) of (Abel et al.
Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013)).
These results are then substituted back into (E 17) to arrive at
If we also use
then we obtain
To find a full expression for the original nonlinear term, we need to also handle the Boltzmann-like pieces of
![]() $\unicode[STIX]{x1D6FF}f_{s}$
.
$\unicode[STIX]{x1D6FF}f_{s}$
.
For the electrons this is simple, and we obtain
where gyroaverages have been removed as the electron gyroradius is smaller than all scales of interest. The first term will vanish when summing over the signs of
![]() $w_{\Vert }$
and so does not appear in any resulting equations.
$w_{\Vert }$
and so does not appear in any resulting equations.
For the ions, we can neglect terms involving
![]() $w_{\Vert }$
as they are small in the mass ratio compared to the same terms for electrons. Thus we have
$w_{\Vert }$
as they are small in the mass ratio compared to the same terms for electrons. Thus we have
because all the non-adiabatic pieces only contain terms proportional to
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
, which vanish under the turbulence average.
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
, which vanish under the turbulence average.
Appendix F. Matching to multiscale gyrokinetics
In this appendix we detail how our inter-ELM transport equations can be matched at the top of the pedestal to multiscale gyrokinetics. We will demonstrate that there exists a subsidiary expansion of multiscale gyrokinetics and a different subsidiary expansion of our inter-ELM equations that both result in the same system of equations. In the main text we have explained the concepts behind these subsidiary orderings, and provided the orderings themselves. Thus, all that remains is to actually perform the subsidiary expansions.
F.1 Subsidiary expansion of multiscale gyrokinetics
In this section we now apply the ordering from § 4.2 to the low-Mach-number equations of Abel et al. (Reference Abel, Plunk, Wang, Barnes, Cowley, Dorland and Schekochihin2013) (henceforth in this appendix we will refer to this as paper I, and refer to equations in that reference with a prefix I-). Consistently with the ordering discussed in § 4.2, we drop all flow-related terms, either because they are small, or because their shear is small and so they can be removed by a Galilean transformation. Taking (I-248) and retaining the leading order in
![]() $\unicode[STIX]{x1D709}$
, the gyrokinetic equation for ions is,
$\unicode[STIX]{x1D709}$
, the gyrokinetic equation for ions is,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}t}}+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}-\left\langle C_{L}\left[h_{i}\right]\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{Z_{i}eF_{0i}}{T_{i}}}{\displaystyle \frac{\unicode[STIX]{x2202}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}}{\unicode[STIX]{x2202}t}}-\frac{c}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}{\displaystyle \frac{\unicode[STIX]{x2202}F_{0s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}t}}+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{i}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}-\left\langle C_{L}\left[h_{i}\right]\right\rangle _{\boldsymbol{R}}\nonumber\\ \displaystyle & & \displaystyle \quad =\,{\displaystyle \frac{Z_{i}eF_{0i}}{T_{i}}}{\displaystyle \frac{\unicode[STIX]{x2202}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}}{\unicode[STIX]{x2202}t}}-\frac{c}{B}\boldsymbol{b}\times \unicode[STIX]{x1D735}\left\langle \unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right\rangle _{\boldsymbol{R}}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}{\displaystyle \frac{\unicode[STIX]{x2202}F_{0s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}},\end{eqnarray}$$
where we have used the definition (I-250) of
![]() $\unicode[STIX]{x1D712}$
and the orderings for the magnetic field to replace
$\unicode[STIX]{x1D712}$
and the orderings for the magnetic field to replace
![]() $\unicode[STIX]{x1D712}$
with
$\unicode[STIX]{x1D712}$
with
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
in this equation. For electrons, we have
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
in this equation. For electrons, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}h_{e}}{\unicode[STIX]{x2202}t}}+\left[v_{\Vert }\left(\boldsymbol{b}+\unicode[STIX]{x1D6FF}\boldsymbol{b}\right)+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right]\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{e}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}-C_{L}\left[h_{e}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,-{\displaystyle \frac{eF_{0e}}{T_{e}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D712}}{\unicode[STIX]{x2202}t}}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{0s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D712}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle {\displaystyle \frac{\unicode[STIX]{x2202}h_{e}}{\unicode[STIX]{x2202}t}}+\left[v_{\Vert }\left(\boldsymbol{b}+\unicode[STIX]{x1D6FF}\boldsymbol{b}\right)+{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}\right]\boldsymbol{\cdot }{\displaystyle \frac{\unicode[STIX]{x2202}h_{e}}{\unicode[STIX]{x2202}\boldsymbol{R}_{s}}}-C_{L}\left[h_{e}\right]\nonumber\\ \displaystyle & & \displaystyle \quad =\,-{\displaystyle \frac{eF_{0e}}{T_{e}}}{\displaystyle \frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D712}}{\unicode[STIX]{x2202}t}}-{\displaystyle \frac{\unicode[STIX]{x2202}F_{0s}}{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}}}{\displaystyle \frac{c}{B}}\boldsymbol{b}\times \unicode[STIX]{x1D735}\unicode[STIX]{x1D712}\boldsymbol{\cdot }\unicode[STIX]{x1D735}\unicode[STIX]{x1D713},\end{eqnarray}$$
where here we have been able to drop all gyroaverages because
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim \unicode[STIX]{x1D709}\ll 1$
. Because of the ordering of
$k_{\bot }\unicode[STIX]{x1D70C}_{e}\sim \unicode[STIX]{x1D709}\ll 1$
. Because of the ordering of
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }$
,
$\unicode[STIX]{x1D6FF}B_{\Vert }$
,
![]() $\unicode[STIX]{x1D712}$
is now given by the simpler form
$\unicode[STIX]{x1D712}$
is now given by the simpler form
As the flow is subsonic, we have replaced
![]() $w_{\Vert }\approx v_{\Vert }$
in these expressions. In addition, we have the field equations (I-251) and (I-149)
$w_{\Vert }\approx v_{\Vert }$
in these expressions. In addition, we have the field equations (I-251) and (I-149)
and
which determine
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
![]() $\unicode[STIX]{x1D6FF}A_{\Vert }$
respectively.
$\unicode[STIX]{x1D6FF}A_{\Vert }$
respectively.
Turning now to the transport equations, we first have (I-252), for particle transport
in which we have not dropped any terms, because the time scale of the sources and the evolution of the equilibrium is defined by the turbulent transport time. So all terms are of the same order in
![]() $\unicode[STIX]{x1D709}$
by definition. However, evaluating the terms in the particle flux (I-170) gives
$\unicode[STIX]{x1D709}$
by definition. However, evaluating the terms in the particle flux (I-170) gives
where we have dropped both collisional transport terms as they are
![]() $O(\unicode[STIX]{x1D708}_{ss}\unicode[STIX]{x1D70C}_{s}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|/L_{\bot })$
, and we have dropped the electric field term as
$O(\unicode[STIX]{x1D708}_{ss}\unicode[STIX]{x1D70C}_{s}^{2}|\unicode[STIX]{x1D735}\unicode[STIX]{x1D713}|/L_{\bot })$
, and we have dropped the electric field term as
![]() $\left\langle \boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\right\rangle _{\unicode[STIX]{x1D713}}$
is small in the mass ratio (see appendix C of Abel & Cowley (Reference Abel and Cowley2013)). Secondly, we have the pressure evolution equation (I-254):
$\left\langle \boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\right\rangle _{\unicode[STIX]{x1D713}}$
is small in the mass ratio (see appendix C of Abel & Cowley (Reference Abel and Cowley2013)). Secondly, we have the pressure evolution equation (I-254):
where again we have dropped the flow related terms, including the viscous heating, because the shearing rate is small, and the ohmic heating is dropped because
![]() $\left\langle \boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\right\rangle _{\unicode[STIX]{x1D713}}$
is small in the mass ratio. Similarly, the collisional energy exchange term is small. The heat flux is now
$\left\langle \boldsymbol{E}\boldsymbol{\cdot }\boldsymbol{B}\right\rangle _{\unicode[STIX]{x1D713}}$
is small in the mass ratio. Similarly, the collisional energy exchange term is small. The heat flux is now
and the turbulent heating is given by (I-259):
Examining the size of the terms in this formula, we immediately see that the turbulent heating occurs on a rate
one order in
![]() $\unicode[STIX]{x1D709}$
too small to appear in our transport equation. This is due to the fact that the rate of perpendicular transport is enhanced by a power of
$\unicode[STIX]{x1D709}$
too small to appear in our transport equation. This is due to the fact that the rate of perpendicular transport is enhanced by a power of
![]() $\unicode[STIX]{x1D709}$
due to the decreasing distance
$\unicode[STIX]{x1D709}$
due to the decreasing distance
![]() $L_{\bot }$
over which transport has to occur, whilst both terms benefit from the increased amplitude and frequency of the turbulence.
$L_{\bot }$
over which transport has to occur, whilst both terms benefit from the increased amplitude and frequency of the turbulence.
At this point we have to make an assumption on the background magnetic field. We will assume that
![]() $\unicode[STIX]{x1D713}$
does not change by
$\unicode[STIX]{x1D713}$
does not change by
![]() $O(1)$
on the transport time scale – this is for consistency with our
$O(1)$
on the transport time scale – this is for consistency with our
![]() $\unicode[STIX]{x1D6FD}$
ordering. Thus, we order
$\unicode[STIX]{x1D6FD}$
ordering. Thus, we order
Applying this ordering means that we drop the compressional heating term
![]() $P_{s}^{\text{comp}}$
from (F 8). Thus, there are no heat sources in our transport equation save for the explicit source.
$P_{s}^{\text{comp}}$
from (F 8). Thus, there are no heat sources in our transport equation save for the explicit source.
F.2 Subsidiary expansion of inter-ELM equations
Now we turn to obtaining the same equations from the inter-ELM system. We apply our subsidiary ordering first to (3.20) to find
so, to lowest order in
![]() $\unicode[STIX]{x1D701}$
,
$\unicode[STIX]{x1D701}$
,
![]() $\unicode[STIX]{x1D711}=\overline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D713})$
. Then the ion kinetic equation (3.17), to lowest order in
$\unicode[STIX]{x1D711}=\overline{\unicode[STIX]{x1D711}}(\unicode[STIX]{x1D713})$
. Then the ion kinetic equation (3.17), to lowest order in
![]() $\unicode[STIX]{x1D701}$
, becomes
$\unicode[STIX]{x1D701}$
, becomes
The general solution of this equation is, by the usual arguments, a stationary Maxwellian, with no parallel flow (i.e.
![]() $u_{\Vert i}\ll v_{\text{th}_{i}}$
). In addition, the ion densities and temperatures are functions only of
$u_{\Vert i}\ll v_{\text{th}_{i}}$
). In addition, the ion densities and temperatures are functions only of
![]() $\unicode[STIX]{x1D713}$
.
$\unicode[STIX]{x1D713}$
.
Examining parallel Ampère’s law, we see that
and so, as the shear length
![]() $L_{s}$
gets longer as
$L_{s}$
gets longer as
![]() $\unicode[STIX]{x1D701}^{-1}$
, we have that the electron parallel flow is also small in
$\unicode[STIX]{x1D701}^{-1}$
, we have that the electron parallel flow is also small in
![]() $\unicode[STIX]{x1D701}$
relative to the ion sound speed. Again, the electron density is now a flux function to lowest order in
$\unicode[STIX]{x1D701}$
relative to the ion sound speed. Again, the electron density is now a flux function to lowest order in
![]() $\unicode[STIX]{x1D701}$
. This in fact holds to two orders in
$\unicode[STIX]{x1D701}$
. This in fact holds to two orders in
![]() $\unicode[STIX]{x1D701}$
as we can iterate (F 13) to show
$\unicode[STIX]{x1D701}$
as we can iterate (F 13) to show
![]() $\unicode[STIX]{x1D711}$
is a flux function to
$\unicode[STIX]{x1D711}$
is a flux function to
![]() $O(\unicode[STIX]{x1D701}^{2})$
, assume axisymmetry and repeat the above argument.
$O(\unicode[STIX]{x1D701}^{2})$
, assume axisymmetry and repeat the above argument.
As the ions are Maxwellian, we can integrate (3.17) over all velocities to find a continuity equation equivalent to (3.14) for the electrons. Flux-surface averaging any one of these continuity equations, we obtain
where we have used identities from section 3.4 of I for the flux-surface averages. This is the same transport equation as we obtained from gyrokinetics.
Multiplying (3.17) by
![]() $\unicode[STIX]{x1D700}_{s}-3T_{s}/2$
, and integrating gives us the following heat transport equation
$\unicode[STIX]{x1D700}_{s}-3T_{s}/2$
, and integrating gives us the following heat transport equation
which, upon using the usual identities for the flux-surface average becomes the gyrokinetic heat transport equation. Similarly, taking (3.16) and using our solution for the mean potential and the electron parallel velocity, we arrive at the same equation. Thus, all heat transport equations match.
However, we still need to show that the equations governing
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D711}$
and
![]() $h_{s}$
are also the same. Using our Maxwellian solution for
$h_{s}$
are also the same. Using our Maxwellian solution for
![]() $f_{i}$
in (3.23), we have that
$f_{i}$
in (3.23), we have that
where we have used the fact that the differences between the energy variable used here and the one defined by (I-241) are all negligible in
![]() $\unicode[STIX]{x1D701}$
. Similarly the distinction between the exact
$\unicode[STIX]{x1D701}$
. Similarly the distinction between the exact
![]() $\unicode[STIX]{x1D707}_{s}$
that we use here and the lowest-order one used in paper I can also be ignored. We have also used the fact that we can transform the mean flow out of this equation due to its low shear. For the electrons there is no such difficulty, there are no flow terms in (3.25) and it is already in exactly the same form as the equation derived from gyrokinetics. The field equations also trivially match in this limit. Thus, we have proved what we set out to. The two subsidiary expansions given in § 4.2 result in identical sets of equations for the pedestal top region.
$\unicode[STIX]{x1D707}_{s}$
that we use here and the lowest-order one used in paper I can also be ignored. We have also used the fact that we can transform the mean flow out of this equation due to its low shear. For the electrons there is no such difficulty, there are no flow terms in (3.25) and it is already in exactly the same form as the equation derived from gyrokinetics. The field equations also trivially match in this limit. Thus, we have proved what we set out to. The two subsidiary expansions given in § 4.2 result in identical sets of equations for the pedestal top region.