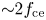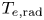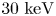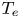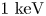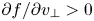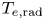Modelling of the electron cyclotron emission burst from a laboratory tokamak plasma with loss-cone maser instability

Abstract

The maser instability associated with the loss-cone distribution has been widely invoked to explain the radio bursts observed in the astrophysical plasma environment, such as aurora and corona. In the laboratory plasma of a tokamak, events reminiscent of these radio bursts have also been frequently observed as an electron cyclotron emission (ECE) burst in the microwave range ($\mathrm{\sim }2{f_{\textrm{ce}}}$ near the last closed flux surface) during transient magnetohydrodynamic events. These bursts have a short duration of ~10 μs and display a radiation spectrum corresponding to a radiation temperature ${T_{e,\textrm{rad}}}$ of over $30\ \textrm{keV}$ while the edge thermal electron temperature ${T_e}$ is only in the range of $1\ \textrm{keV}$. Suprathermal electrons can be generated through magnetic reconnection, and a loss-cone distribution can be generated through open stochastic field lines in the magnetic mirror of the near-edge region of a tokamak plasma. Radiation modelling shows that a sharp distribution gradient $\partial f/\partial {v_ \bot } > 0$ at the loss-cone boundary can cause a negative absorption of ECE radiation through the maser instability. The negative absorption then amplifies the radiation so that the microwave intensity is significantly stronger than the thermal value. The significant ${T_{e,\textrm{rad}}}$ from the simulations suggests the potential role of the loss-cone maser instability in generating the ECE burst in a tokamak.

1. Introduction

Radio bursts have been observed in relation to astrophysical magnetic reconnection events, such as reconnection from solar flares (Aurass, Vršnak & Mann 2002), magnetar (Lyubarsky 2020) and the Earth's magnetosphere (Balcerak 2013; Fogg et al. 2022). In a magnetically confined laboratory plasma in a tokamak, microwave bursts reminiscent of astrophysical radio bursts are robustly observed near the second-harmonic electron cyclotron frequency (hence called the electron cyclotron emission (ECE) burst (Fuchs & Austin 2001; Freethy et al. 2015a)). These bursts robustly accompany one particular type of reconnection magnetohydrodynamic (MHD) event, called the edge-localized mode (ELM) (Ertl, Jüttner & Asdex TEAM 1985; Yang et al. 2018), in a tokamak plasma. Magnetic reconnection can happen near the surface (edge) of the tokamak plasma during ELM when the plasma has an H-mode (high) confinement. It releases transient heat load with hot plasma particles to the tokamak plasma-facing materials. The heat load can damage the material in a reactor-level tokamak environment; hence it has been an important research topic to mitigate the ELM heat load (Kim et al. 2024; Li et al. 2024b) in present experimental tokamak devices. There are also other bursts (Barada 2024; Teo et al. 2024) in the microwave range away from the ECE harmonic frequency associated with ELMs. Thus, it is of fundamental interest to understand the mechanism of the ECE burst in a tokamak laboratory plasma. On the one hand, the physical mechanism can provide the basis for using tokamak plasmas to study the radio burst from astrophysical reconnection events (McClements 2019). On the other hand, understanding the physics of the ECE burst improves knowledge of electron kinetics during ELMs in a tokamak plasma.

Dedicated modelling efforts have been applied to understand the ELM ECE burst from the tokamak community. The measured ECE radiation is a result of two processes: emission and absorption (Bornatici et al. 1983). Thus, high emission from suprathermal electrons (Li et al. 2017, 2019), reduced absorption from an ELM cold pulse (Janos et al. 1996), negative absorption from runaway electron maser instability (Kurzan & Steuer 1997), anomalous Doppler instability (Lai, Chapman & Dendy 2013, 2015; Freethy et al. 2015b; McClements et al. 2017), cold–hot wave coupling (Lee, Ji & Yun 2020) and energy anisotropy (Lee, Yun & Ji 2022) have all been proposed to explain the burst. In this research, we discuss the role of negative absorption from the suprathermal electron loss-cone maser instability, opposing the role of suprathermal electron emission, in generating the observed ECE burst.

Before moving to the major content, we emphasize that the formation of suprathermal electrons and loss-cone distribution from ELMs is outside the scope of this research. There is also literature speculating that the suprathermal electron maser instability is responsible for tokamak microwave bursts (Taylor & Mansfield 1998; Rozhedestvensky et al. 2015; Buratti et al. 2021). This research focuses on the ECE radiation part where the suprathermal electron distributions are analytically assumed. This research stands out against other tokamak microwave burst research as it highlights the maser instability driven by the loss-cone distribution and systematically models the corresponding radiation intensity.

The paper is organized as follows. In § 2 we introduce the tokamak magnetic configuration and one example of the ECE burst observation. In § 3 we introduce how to model the ECE and absorption in a tokamak system. In § 4 we demonstrate the simulated ECE radiation intensity much greater than the thermal level from the loss-cone maser instability. In § 5 we support the role of the maser instability (negative absorption) by demonstrating why the high emission alone cannot be responsible for the burst. Section 6 presents a discussion and § 7 the conclusion.

2. The tokamak magnetic configuration and the ECE burst observation

The plasma device of a tokamak uses closed magnetic field lines to confine the charged particles in a torus. In this plasma torus, the magnetic field contains two components, poloidal field ${B_p}$ and toroidal field ${B_t}$, shown in the two-dimensional cross-section of the tokamak in figure 1. The toroidal field (~1.5 T) is the magnetic field in the toroidal direction generated by external D-shape magnetic coils. The poloidal field (~0.3 T) is the magnetic field in the poloidal direction generated by the plasma current that flows in the toroidal direction. The resulting helical magnetic field line forms a flux surface, where charged particles can only travel on the magnetic field line on the same flux surface. The edge of the plasma is defined by the last closed flux surface (LCFS), shown as the dashed line in figure 1. Outside the magnetically confined plasma edge, the magnetic field line is open and directly connected with the plasma target (blue solid line). On the LCFS, electrons follow the helical field line and eventually get lost at the target, called the divertor, at $(R,Z) = (1.5\ \textrm{m},\; - 1.25\ \textrm{m})$ in figure 1.

Figure 1. Two-dimensional cross-section of a tokamak plasma.

The ECE diagnostic measures the millimetre-wave radiation from the plasma. The diagnostic system resolves the radiation intensity ${T_{e,\textrm{rad}}}$ and the millimetre-wave frequency. In the DIII-D tokamak (Fenstermacher et al. 2022), there are two ECE diagnostic systems: one is the ECE radiometer (Austin & Lohr 2003) and the other is the W-band ECE-imaging system (Zhu et al. 2020). The two diagnostics are typically used to visualize the electron temperature profile (Xie et al. 2024) and MHD events (Yu et al. 2021a, 2023; Khabanov et al. 2024) by measuring millimetre-wave radiation from $75$ to $129.5\ \textrm{GHz}$. In a tokamak, this radiation is typically caused by the interaction between the electrons and waves near the second harmonic of the electron cyclotron frequency ${\omega _{\textrm{ce}}} = e|B|/{m_e}$, where $|B|$ is the magnetic field strength. As $|B|$ monotonically decreases with the major radius R and can be accurately reconstructed, one can resolve the source of the radiation at a specific radial location R by the wave frequency.

The ELM is a transient MHD event localized to the edge of the tokamak plasma, shown as the filament structure at the surface of a tokamak plasma in figure 2. Each ELM causes a discrete burst in the ${D_\alpha }$ emission (shown in figure 3c), which is the recycling emission from deuterium gas near the plasma edge. When an ELM occurs, the closed field lines between different flux surfaces can reconnect, causing a transient heat load from the plasma edge to the divertor. The physics of the mechanism of ELM trigger (Snyder et al. 2002) has been well established in the tokamak community. One trigger mechanism is the peeling mode (Li et al. 2022), which is an MHD kink instability driven by the plasma current. The other mechanism is the ballooning mode (Ozeki et al. 1990), which is an MHD interchange instability driven by the pressure gradient. Thus, the ELM is an ideal laboratory plasma phenomenon to study reconnection radio burst triggered by different modes.

Figure 2. Visible-light image of the ELM in the MAST-U tokamak (Kirk et al. 2007). (© IOP Publishing. Reproduced with permission. All rights reserved.)

Figure 3. The DIII-D ECE diagnostic robustly observes ECE bursts. (a) The ECE radiation intensity at the second-harmonic frequency near the plasma edge. (b) The ECE radiation intensity at the third-harmonic frequency near the plasma edge. (c) The recycling light from deuterium gas. (d) Zoomed view of the second-harmonic ECE. (e) Zoomed view of ${D_\alpha }$.

In the DIII-D tokamak, each ELM event is robustly accompanied by bursts on the ECE diagnostic signal, shown in figure 3(a). These ECE bursts appear at the microwave frequency near the second-harmonic electron cyclotron frequency at the plasma edge and have a radiation intensity ${T_{e,\textrm{rad}}}$ of more than $30\ \textrm{keV}$, while the local thermal electron temperature ${T_e} < 500\ \textrm{eV}$. Here, we restate that ${T_{e,\textrm{rad}}}$ is the radiation intensity seen by the ECE receiver in units of $\textrm{keV}$. Radiation intensity ${T_{e,\textrm{rad}}}$ is equal to ${T_e}$ when the electrons strictly follow the Maxwellian distribution. It is also noticeable that this burst does not appear at the third-harmonic ECE frequency (figure 3b) near the plasma edge. This research aims to evaluate the loss-cone maser instability explaining the second-harmonic ECE burst and the absence of ECE burst at the third-harmonic frequency during ELM in the DIII-D tokamak.

It is worth noting that the microwave bursts on the ECE diagnostics have been shown not to be a non-ideal instrumental effect, where for example microwaves away from the receiver frequency band appear on the diagnostic signal, or large electromagnetic bursts during ELM causing the system to behave abnormally. In the DIII-D tokamak, this phenomenon is independently observed by both ECE and ECE imaging diagnostics, which use very different techniques to measure the microwave radiation in terms of optics (Xie et al. 2020; Li et al. 2021), waveguide (Qiu et al. 2024), power supply and electronics (Zhu et al. 2018) and receiver technology (Chen et al. 2021; Zhu et al. 2021, 2022; Zheng et al. 2022; Li et al. 2024a).

An ELM is a magnetic reconnection event where charged particles can be accelerated to suprathermal energies. The energized electrons can significantly alter the microwave transport process and hence make ${T_{e,\textrm{rad}}} \ne {T_e}$. The mechanism that connects the suprathermal electrons to the ECE burst varies. Some candidate mechanisms are the high emission from suprathermal electrons’ high perpendicular energy and negative absorption from suprathermal electron anomalous Doppler instability. The loss-cone maser instability is a well-established theoretical mechanism applied to explain astrophysical radio bursts (Melrose, Hewitt & Dulk 1984; Sharma & Vlahos 1984; Wu 1985; Aschwanden 1990; Ergun et al. 2000; Treumann 2006; Treumann & Baumjohann 2017) in aurora kilometre radiation, solar corona and other astrophysical reconnection events. Such a distribution can also appear in a tokamak system. In this research, we use the loss-cone maser instability to explain how such a high radiation temperature can be generated from suprathermal electrons during an ELM reconnection event.

3. Fundamentals of ECE radiation

The cyclotron motion of electrons interacts with microwaves near the nth harmonics of the electron cyclotron frequency ${\omega _{\textrm{ce}}} = eB/m$. Here e is the electron charge, B is the magnetic field strength and m is the static electron mass. Microwave–electron interaction here refers to the microwave emission and absorption by electrons. A horizontally outward-propagating microwave gets both emitted and absorbed by the electrons, following the ECE transport equation (Bornatici et al. 1983):

(3.1)\begin{equation}\frac{\textrm{d}}{{\textrm{d}R}}\left[ {\frac{{I(\omega ,R)}}{{N_r^2(\omega ,R)}}} \right] = \frac{1}{{N_r^2(\omega ,R)}}[ - \alpha (\omega ,R)I(\omega ,R) + j(\omega ,R)],\end{equation}

where $\alpha (\omega )$ is the absorption coefficient at microwave frequency $\omega$, $j(\omega )$ is the emission coefficient, ${N_r}(\omega ,R)$ is the plasma refractive index, $I(\omega ,R)$ is the emission intensity and R is the tokamak major radius. For simplicity, we represent ${T_{e,\textrm{rad}}} = ({\omega ^2}/8{{\rm \pi}^3}N_r^2{c^2})I$ and $J = ({\omega ^2}/8{{\rm \pi}^3}N_r^2{c^2})j$. Equation (3.1) can then be presented in the form

(3.2)\begin{equation}\frac{{\textrm{d}{T_{e,\textrm{rad}}}(\omega ,R)}}{{\textrm{d}R}} = [ - \alpha (\omega ){T_{e,\textrm{rad}}}(\omega ,R) + J(\omega ,R)].\end{equation}

In (3.2), each term is of a straightforward physical unit: ${T_{e,\textrm{rad}}}$ has the same units as electron temperature ${T_e}$ in $\textrm{keV}$, R is in units of $\textrm{cm}$, the absorption coefficient $\alpha$ is in units of $\textrm{rad}\ \textrm{c}{\textrm{m}^{ - 1}}$ and emission coefficient J is in units of $\textrm{keV}\ \textrm{c}{\textrm{m}^{ - 1}}$. For positive $\alpha$, ${T_{e,\textrm{rad}}}$ converges to $J/\alpha$ at a large value of R. For negative $\alpha$, ${T_{e,\textrm{rad}}}$ does not converge to $J/\alpha$ at a large R, so ${T_{e,\textrm{rad}}}$ can only be calculated solving the whole transport equation.

Only certain electrons in the velocity space $({v_ \bot },{v_\parallel })$ can resonate with the microwave at frequency $\omega$, hence contributing to the emission and absorption coefficient. The resonance condition is

(3.3)\begin{equation}\gamma - \frac{{{k_\parallel }{v_\parallel }}}{\omega } - n{\omega _{\textrm{ce}}} = 0.\end{equation}

Here, $\gamma$ is the Lorentz factor, ${k_\parallel }$ is the wavenumber of the microwave parallel to the magnetic field line, ${v_\parallel }$ is the electron parallel velocity, ${k_\parallel }$ is the wavenumber of the microwave parallel to the magnetic field and n is the harmonic number.

The resonant condition (3.3) points to a half-ellipse (Hewitt, Melrose & Rönnmark 1982) in electron velocity space, shown in figure 4(b). The ECE receiver measures the microwaves that propagate radially outward in the plasma. These microwaves can have a finite angle $\theta$ with respect to the radial direction, shown in figure 4(a). Resonant interaction can exist when the local cyclotron harmonic frequency $n{\omega _{\textrm{ce}}}$ is close to the microwave frequency $\omega$. A resonant ellipse can be drawn with different $\omega /n{\omega _{\textrm{ce}}}$ and propagation angles $\theta$. Only electrons on this resonant ellipse in velocity space can contribute to microwave emission and absorption.

Figure 4. Two resonant ellipses of different oblique angles and frequencies $\omega /n{\omega _{\textrm{ce}}}$ are plotted on a 3 keV Maxwellian electron velocity phase space. (a) The microwave propagation geometry. (b) The resonant ellipses on a Maxwellian electron velocity distribution.

The emission coefficient J and absorption coefficient $\alpha$ can be qualitatively understood with formulae integrating the electron distribution f and distribution gradient $\partial f/\partial {v_ \bot }$ on the resonant ellipse:

(3.4)\begin{gather}\alpha \sim- \iint\!\!\!\int {\partial f/\partial {v_ \bot }{\epsilon _a}\,\textrm{d}{v^3}} \delta \left( {\gamma - \frac{{{k_\parallel }{v_\parallel }}}{\omega } - n{\omega_{\textrm{ce}}}} \right),\end{gather}

(3.5)\begin{gather}J\sim \iint\!\!\!\int {f{\epsilon _a}\,\textrm{d}{v^3}} \delta \left( {\gamma - \frac{{{k_\parallel }{v_\parallel }}}{\omega } - n{\omega_{\textrm{ce}}}} \right).\end{gather}

Here, f is the electron velocity distribution function, ${\epsilon _a}$ is the anti-Hermitian dielectric tensor and $\delta$ function represents the resonant condition. From this formula, one can easily deduce that ${T_{e,\textrm{rad}}}(\omega ) = J(\omega )/\alpha (\omega ) = f/(\partial f/\partial {v_ \bot }) = {T_e}$ when the electron distribution function follows the Maxwellian distribution. This is the principle of how ECE is used to measure the electron temperature in a tokamak.

ECE radiation modelling is a well-established field to design diagnostics (Yu et al. 2022c), to extend diagnostic capability (Yu et al. 2022b), to perform MHD modelling validation (Taimourzadeh et al. 2019; Van Zeeland et al. 2024) and to improve data interpretation (Yu et al. 2022a) in a tokamak. The ECE modelling tool is coded (Yu et al. 2024) and performed on the OMFIT platform (Meneghini et al. 2015; Yu et al. 2021), where we apply radiation modelling to explain the ECE burst with the loss-cone maser instability.

4. Explaining ECE burst with loss-cone maser instability

4.1. The layout of the simulation

We simulate the outward microwave propagation process in this section. An ELM is an MHD instability localized to the plasma edge. Thus, for the ECE burst, we expect the microwave intensity to remain at the thermal value in the core plasma and rise to non-thermal levels $({T_{e,\textrm{rad}}} \ge 30\ \textrm{keV})$ only at the plasma edge as it propagates outward. Using a typical DIII-D tokamak equilibrium, the LCFS is at $R = 225\ \textrm{cm}$ where ${f_{\textrm{ce}}} = 40\ \textrm{GHz}$, shown in figure 5. We choose to model the microwave of X-mode polarization, $\textrm{frequency} = 80.5\ \textrm{GHz}$, and oblique angle of $12\mathrm{^\circ }$. The wave polarization and frequency are chosen as we mostly observe the ECE bursts with an X-mode receiver and frequency near $2{f_{\textrm{ce}}}$ at the LCFS experimentally. We assume thermal electron temperature ${T_e} = 2\ \textrm{keV}$ at $R < 224\ \textrm{cm}$ and suprathermal electrons at $224\ \textrm{cm} < R < 225\ \textrm{cm}$. These suprathermal electrons are generated by the ELM reconnection event and play the key role in amplifying the microwave intensity to the observed burst level.

Figure 5. Layout of the simulation domain. The model simulates the microwave outward propagation through the plasma edge where suprathermal electrons are expected to amplify the wave to the burst level $({T_{e,\textrm{rad}}} \ge 30\ \textrm{keV})$.

The key to the maser instability is a $\partial f/\partial {v_ \bot } > 0$ region in the electron velocity distribution. In this research, we highlight the $\partial f/\partial {v_ \bot } > 0$ source caused by the loss-cone distribution. In a tokamak, the magnetic field is stronger at the divertor (red dot at R = 1.5 m in figure 6a) than at the midplane plasma edge (red dot at R = 2.25 m in figure 6a). This configuration resembles a magnetic mirror and hence leads to loss-cone distribution with a loss-cone angle of $55\mathrm{^\circ }$, shown in figure 6(b).

Figure 6. Demonstration of the loss-cone distribution brought by the open stochastic field line in the tokamak configuration. (a) The tokamak magnetic configuration. (b) The loss-cone distribution at the midplane plasma edge causing $\partial f/\partial {v_ \bot } > 0$ near the loss-cone boundary.

During the ELM reconnection event, a stochastic field connects the flux surfaces near the plasma inside the LCFS. The field line can be directly connected to the divertor, and electrons can lose confinement by following the magnetic field line to the divertor (red dot at R = 1.5 m in figure 6a). However, on the midplane near the plasma edge (red dot at R = 2.25 m in figure 6a), only electrons of a high $|{v_\parallel }/{v_ \bot }|$ can arrive at the divertor following the field line. Electrons of a low $|{v_\parallel }/{v_ \bot }|$ can stay confined as they cannot arrive at the divertor due to electron adiabatic invariance. Thus, midplane edge electrons will form a loss-cone velocity distribution. At the loss-cone boundary in the velocity domain, one can expect a step function where the electron population stays confined and accumulates above the boundary (figure 6b), while disappearing to almost zero below the boundary. This step function will be relaxed when neutrals and collisions scatter confined electrons to the loss-cone region. Using the DIII-D magnetic configuration, we can draw the loss-cone boundary with a loss-cone angle of ${\theta _{\textrm{loss}}} = 55\mathrm{^\circ }$, as shown in figure 6(b). Here, the loss-cone angle is calculated using the formula for a magnetic mirror:

(4.1)\begin{equation}\tan ({\theta _{\textrm{loss}}}) = \sqrt {\frac{{{B_{\textrm{min}}}}}{{{B_{\textrm{max}}}}}} ,\end{equation}

where ${B_{\textrm{min}}}$ is the magnetic field strength at the midplane outboard plasma edge and ${B_{\textrm{max}}}$ is the magnetic field at the divertor target. In a tokamak, the magnetic field strength $|B|\sim 1/R$, so the loss-cone angle is ${\sim} 55\mathrm{^\circ }$. The loss-cone distribution with the open stochastic field line in a tokamak has also been predicted by magnetic topology analysis and global gyrokinetic simulations in Yoo et al. (2021, 2022).

Figures 7(a) and 7(b) plot the suprathermal electron distribution in the velocity domain for the ECE burst modelling. This work highlights the maser instability drive from the loss-cone distribution. For simplicity, we assume the whole suprathermal population resides in the loss-cone region in the velocity domain, and the sole source of positive $\partial f/\partial {v_ \bot }$ comes from how the electron population varies with the electron pitch angle in the loss cone. In detail, the suprathermal electron density is taken to be ${10^{18}}\;{\textrm{m}^{ - 3}}$, which is $1/10$ of the thermal electron density. The suprathermal electrons have a perpendicular kinetic energy ${E_ \bot } = {\textstyle{1 \over 2}}{m_e}v_ \bot ^2\sim 6\ \textrm{keV}$ and ${v_\parallel }\sim 0.09c$. The distribution is also symmetric around ${v_\parallel } = 0$ to avoid unrealistic current carried by the suprathermal population. Inside the loss cone, the suprathermal population falls as ${\theta ^N}/\theta _{\textrm{loss}}^N$, where $\tan (\theta ) = {v_ \bot }/{v_\parallel }$ and $N = 1000$. Here, N determines how fast the suprathermal electron population drops with respect to pitch angle $\theta$ in the loss-cone region; hence a positive $\partial f/\partial {v_ \bot }$ is created. We discuss the impact of N value and suprathermal electron energy on the ECE burst in the next sections.

Figure 7. The suprathermal electron distribution in the loss-cone region. (a) The loss-cone distribution of suprathermal electrons and Maxwellian electrons. (b) Zoomed view of the suprathermal electrons. The suprathermal electrons have a non-zero population only in the loss-cone region so the loss-cone electrons are the sole source of positive $\partial f/\partial {v_ \bot }$ for maser instability.

4.2. Results of the simulation

The transport modelling shows that the suprathermal electrons at $224\ \textrm{cm} < R < 225\ \textrm{cm}$ can excite a strong ${T_{e,\textrm{rad}}}$ as the microwave propagates outward, shown in figure 8. The absorption and emission coefficients for this $80.5\ \textrm{GHz}$ microwave are respectively plotted in figures 8(a) and 8(b). In the core plasma region (R < 224 cm) where the electrons are Maxwellian, the absorption coefficient is positive (figure 8a). As a result, the radiation intensity ${T_{e,\textrm{rad}}} = J/\alpha = {T_e} = 2\ \textrm{keV}$ (figure 8c) at $R \ge 220\ \textrm{cm}$ in the thermal region. As the microwave moves towards the loss-cone suprathermal electron region ($224\ \textrm{cm} \le R \le 225\ \textrm{cm}$; red region in figure 8), the absorption coefficient becomes significantly negative and reaches $- 15\ \textrm{rad}\ \textrm{c}{\textrm{m}^{ - 1}}$ at the peak resonance location. The radiation intensity also exponentially grows by $\textrm{exp}\left( { - \int_{224\ \textrm{cm}}^{225\ \textrm{cm}} {\alpha \,\textrm{d}R} } \right)$ at the plasma edge and reaches ${T_{e,\textrm{rad}}}\sim 80\ \textrm{keV}$ after leaving the plasma.

Figure 8. The transport process of the $80.5\ \textrm{GHz}$ X-mode microwave propagating outward.

5. The role of emission in generating the burst

The microwave radiation intensity is a result of both emission and absorption. In the last section, we have shown that the negative absorption $\alpha$ from the loss-cone maser instability can generate a large burst. A question can be raised: what role does emission play in the ECE burst? Is it possible that the ECE burst can be generated by strong emission J instead of negative absorption $\alpha$ in the transport equation (3.2)?

Simulations disagree on the important role of emission in generating the ECE burst. As will be shown, on the one hand, a much higher perpendicular suprathermal electron energy is needed to generate the burst without a negative absorption. On the other hand, even if these higher-energy electrons exist during ELM, they should emit a strong burst simultaneously at the second ECE frequency and at the third ECE frequency. However, we rarely observe ECE bursts at the third harmonic in DIII-D (figure 3b) experiments.

Simulation shows that a much larger suprathermal electron perpendicular energy is required with the contribution from emission only (absorption $\alpha = 0$). The emission coefficients are calculated at three ${E_ \bot } = {\textstyle{1 \over 2}}mv_ \bot ^2$ energy levels in figure 9. A suprathermal electron density of $\; {10^{18}}\;{\textrm{m}^{ - 3}}$ is separately placed along the loss-cone boundary in figure 9(a) at ${E_ \bot }\sim 7\ \textrm{keV}$, ${E_ \bot }\sim 15\ \textrm{keV}$ and ${E_ \bot }\sim 27\ \textrm{keV}$. Note that only the right half $({v_\parallel } > 0)$ of the distribution is shown. The corresponding emission coefficients are calculated in figure 9(b). The radiation intensity is ${T_{e,\textrm{rad}}} = \int {J\,\textrm{d}R}$ without absorption, and these energy levels can respectively lead to ${T_{e,\textrm{rad}}}\sim 2,\textrm{ }9$ and $25\ \textrm{keV}$. Therefore, considering only the emission from suprathermal electrons, one needs a high perpendicular energy $({E_ \bot } > 27\ \textrm{keV})$ to generate a burst of ${T_{e,\textrm{rad}}} \ge 30\ \textrm{keV}$.

Figure 9. The emission coefficients are calculated with suprathermal electrons of different perpendicular energies.

At a large perpendicular energy, the emission coefficients are strong at both the second- and third-harmonic frequencies. The emission coefficients are calculated at second- and third-harmonic ECE frequencies for three energy levels. At ${E_ \bot } = 15\ \textrm{keV}$ (figure 10b) or $27\ \textrm{keV}$ (figure 10c), the third-harmonic emission coefficient is $400\ \textrm{eV}\ \textrm{c}{\textrm{m}^{ - 1}}$ or $2000\ \textrm{eV}\ \textrm{c}{\textrm{m}^{ - 1}}$, while the second-harmonic emission coefficient is $9000\ \textrm{eV}\ \textrm{c}{\textrm{m}^{ - 1}}$ or $23\;000\ \textrm{eV}\ \textrm{c}{\textrm{m}^{ - 1}}$. The emission coefficient ratio between the second and third harmonics is 22.5 : 1 at ${E_ \bot } = 15\ \textrm{keV}$ and 11.5 : 1 at ${E_ \bot } = 27\ \textrm{keV}$. In other words, if the suprathermal electron has energy ${E_ \bot } = {\textstyle{1 \over 2}}mv_ \bot ^2\ \textrm{above}\;15\ \textrm{keV}\ \textrm{or}\;27\ \textrm{keV}$, and the emission alone is responsible for the burst of ${T_{e,\textrm{rad}}} = 30\ \textrm{keV}$ at the second-harmonic ECE frequency, one will also see a burst of $\mathrm{\ > }1.3\ \textrm{keV}\ \textrm{or}\;2.6\ \textrm{keV}$ at the third-harmonic frequency.

Figure 10. The emission coefficient becomes non-negligible at the third harmonic for ${E_ \bot } = {\textstyle{1 \over 2}}mv_ \bot ^2 > 15\ \textrm{keV}$. The emission coefficient spectrum at the second-harmonic frequency for three suprathermal energy levels. The emission coefficient at the second- and third-harmonic frequencies for (a) ${E_ \bot }\sim 7\ \textrm{keV}$, (b) ${E_ \bot }\sim 15\ \textrm{keV}$ and (c) ${E_ \bot }\sim 27\ \textrm{keV}$.

From the simulation in figures 9 and 10, one can draw a contrast using the high emission J from suprathermal electrons to explain the burst. On the one hand, a high ${E_ \bot }\textrm{ }( > 27\ \textrm{keV})$ is needed to generate the observed burst $({T_{e,\textrm{rad}}} > 30\ \textrm{keV)}$. On the other hand, such a high ${E_ \bot }$ will also generate the ECE burst at the third-harmonic ECE frequency. However, such a burst at the third-harmonic ECE frequency is rarely observed in DIII-D tokamak experiments, shown in figure 3(c).

6. Discussion

We have shown in § 4 that the loss-cone maser instability (negative absorption $\alpha$) can drive an ECE burst. We have also shown in § 5 that a strong emission with zero ECE reabsorption can also generate the radiation intensity at the experimental burst level. Though both can generate the ECE burst much higher than the thermal radiation, we favour the role of negative absorption over the emission in generating the burst in this work. This is because the burst radiation should be visible at both second- and third-harmonic ECE frequencies if emission plays the dominant role, while for DIII-D, we rarely observe an ECE burst at the third-harmonic frequency.

However, we must admit that there is also difficulty using the loss-cone negative absorption to generate the microwave burst, as a crowded suprathermal electron distribution (large $\partial f/\partial {v_ \bot }$) near the loss-cone boundary is required for the modelled radiation to reach the experimental burst level.

The suprathermal electron population f is assumed to fall as ${\theta ^N}/\theta _{\textrm{loss}}^N$ in the loss cone in this investigation, where $\tan (\theta ) = {v_ \bot }/{v_\parallel }$ and ${\theta _{\textrm{loss}}}$ is the loss-cone angle. Here N is the steepness factor that governs how fast the suprathermal population drops in the loss-cone region. Making the suprathermal electron density ${10^{18}}\;{\textrm{m}^{ - 3}}$, the loss-cone suprathermal electron distribution is plotted with $N = 100$ (figure 11a) and $N = 1000$ (figure 11b). Their corresponding absorption values are plotted in figure 11(c). It can easily be seen that a large N (sharper gradient $\partial f/\partial {v_ \bot }$ at the loss-cone boundary) can significantly increase the negative absorption coefficient. The radiation intensity is amplified by ${\textrm{e}^{ - \int {\alpha \,\textrm{d}R} }}$ at the plasma edge. Then, the distribution with $N = 100$ amplifies the wave intensity by 5 times, the distribution with $N = 300$ by 16 times and that with $N = 1000$ by 54 times. Recalling that ${T_{e,\textrm{rad}}}\sim 2\ \textrm{keV}$ before the microwave enters the plasma edge, thus $N > 300$ is needed for the microwave intensity to reach the burst level $({T_{e,\textrm{rad}}} > 30\ \textrm{keV})$. Such a high $\partial f/\partial {v_ \bot }$ implies that suprathermal electrons generated by the ELM magnetic reconnection are distributed in a confined space near the loss-cone boundary in the velocity domain.

Figure 11. The negative absorption coefficient is simulated at different loss-cone steepness factors N. (a) Suprathermal electron distribution with $N = 100$. (b) Suprathermal electron distribution with $N = 1000$. (c) The negative absorption coefficient $\alpha$ calculated with different N values.

7. Conclusion

The tokamak microwave burst during ELMs can be a powerful laboratory platform to study radio burst phenomena from astrophysical magnetic reconnection events. It is thus desired to understand the physical mechanism of the ELM microwave burst in a tokamak. The microwave burst robustly appears and peaks at the second-harmonic ECE frequency near the plasma edge. The transport process of ECE, which involves microwave emission and absorption, is simulated to explain the burst in this research.

In this work, we employ the loss-cone suprathermal maser instability, which is widely applied in astrophysical radio burst physics, in the ECE transport process to explain the burst. The loss-cone distribution is caused by the open stochastic field line due to the magnetic reconnection during ELM and the tokamak magnetic configuration. In the modelling, we assume ${E_ \bot } = {\textstyle{1 \over 2}}mv_ \bot ^2\sim 6\ \textrm{keV}$ and ${10^{18}}\;{\textrm{m}^{ - 3}}$ suprathermal electrons being generated during the ELM reconnection at the plasma edge. A sharp gradient $\partial f/\partial {v_ \bot }$ at the loss-cone boundary can be a source for the maser instability, and is simulated to generate a microwave burst of intensity ${T_{e,\textrm{rad}}}\sim 80\ \textrm{keV}$, sufficiently strong for the experimental value ${T_{e,\textrm{rad}}} > 30\ \textrm{keV}$. This research also shows that the emission alone (making the absorption coefficient $\alpha = 0$) cannot be responsible for the burst in DIII-D. If emission were the sole mechanism, a higher energy $({E_ \bot } \gg 6\ \textrm{keV})$ would be needed and the ECE burst should appear at both the second- and third-harmonic frequencies. However, we rarely observe an ECE burst at the third-harmonic frequency in the DIII-D tokamak.

We emphasize that the loss-cone maser instability is only one candidate mechanism for the tokamak ELM ECE burst. We do not claim it explains the full picture of the ELM-induced ECE burst. A sufficiently high distribution gradient $\partial f/\partial {v_ \bot }$ at the loss-cone boundary in the velocity domain is needed to generate a burst of experimentally relevant value. Such a high $\partial f/\partial {v_ \bot }$ implies that suprathermal electrons generated during ELMs are distributed in a confined space in the velocity domain near the loss-cone boundary. Similar kinetics of ELM acceleration of charged particles to a confined space in the velocity domain have also been observed in experiment (Galdon-Quiroga et al. 2018) and reproduced in simulations (Rivero-Rodríguez et al. 2023) of fast ions. It is of interest to study if electrons can also be accelerated to a confined velocity space during ELMs with a similar mechanism.