Article contents
Magnetic nulls in interacting dipolar fields
Published online by Cambridge University Press: 03 May 2021
Abstract
The prominence of nulls in reconnection theory is due to the expected singular current density and the indeterminacy of field lines at a magnetic null. Electron inertia changes the implications of both features. Magnetic field lines are distinguishable only when their distance of closest approach exceeds a distance 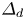 $\varDelta _d$. Electron inertia ensures
$\varDelta _d$. Electron inertia ensures 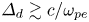 $\varDelta _d\gtrsim c/\omega _{pe}$. The lines that lie within a magnetic flux tube of radius
$\varDelta _d\gtrsim c/\omega _{pe}$. The lines that lie within a magnetic flux tube of radius 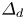 $\varDelta _d$ at the place where the field strength
$\varDelta _d$ at the place where the field strength 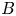 $B$ is strongest are fundamentally indistinguishable. If the tube, somewhere along its length, encloses a point where
$B$ is strongest are fundamentally indistinguishable. If the tube, somewhere along its length, encloses a point where  $B=0$ vanishes, then distinguishable lines come no closer to the null than
$B=0$ vanishes, then distinguishable lines come no closer to the null than 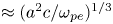 $\approx (a^2c/\omega _{pe})^{1/3}$, where
$\approx (a^2c/\omega _{pe})^{1/3}$, where 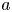 $a$ is a characteristic spatial scale of the magnetic field. The behaviour of the magnetic field lines in the presence of nulls is studied for a dipole embedded in a spatially constant magnetic field. In addition to the implications of distinguishability, a constraint on the current density at a null is obtained, and the time required for thin current sheets to arise is derived.
$a$ is a characteristic spatial scale of the magnetic field. The behaviour of the magnetic field lines in the presence of nulls is studied for a dipole embedded in a spatially constant magnetic field. In addition to the implications of distinguishability, a constraint on the current density at a null is obtained, and the time required for thin current sheets to arise is derived.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 4
- Cited by



