Hostname: page-component-cc8bf7c57-ksm4s Total loading time: 0 Render date: 2024-12-12T01:53:25.899Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear electrostatic gyrokinetics for electron–positron plasmas

Published online by Cambridge University Press:  16 November 2018

D. Kennedy Open the ORCID record for D. Kennedy [Opens in a new window] ,
A. Mishchenko Open the ORCID record for A. Mishchenko [Opens in a new window] ,
P. Xanthopoulos  and
P. Helander
D. Kennedy*
Affiliation:
Max Planck Institute for Plasma Physics, D-17491 Greifswald, Germany
A. Mishchenko
Affiliation:
Max Planck Institute for Plasma Physics, D-17491 Greifswald, Germany
P. Xanthopoulos
Affiliation:
Max Planck Institute for Plasma Physics, D-17491 Greifswald, Germany
P. Helander
Affiliation:
Max Planck Institute for Plasma Physics, D-17491 Greifswald, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Gyrokinetic stability of plasmas in different magnetic geometries is studied numerically using the GENE code. We examine the stability of plasmas, varying the mass ratio between the positive and negative charge carriers, from conventional hydrogen plasmas through to electron–positron plasmas. Stability is studied for prescribed temperature and density gradients in different magnetic geometries: (i) An axisymmetric, circular flux surface, low 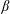$\unicode[STIX]{x1D6FD}$ (tokamak) configuration. (ii) A non-axisymmetric quasi-isodynamic (optimised stellarator) configuration using the geometry of the stellarator Wendelstein 7-X. We also present the analytic theory of trapped particle modes in electron–positron plasmas. We found similar behaviour of the growth rate and real frequency compared to previous studies on the tokamak case. We are able to identify two distinct regimes dominated by modes propagating in the electron diamagnetic direction and modes propagating in the ion/positron diamagnetic direction, depending on the mass ratio. In both the tokamak and the stellarator case we observe that the real frequency tends to zero as the mass ratio approaches unity and are able to explain this using gyrokinetic theory.

Keywords

plasma confinementplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 6 , December 2018 , 905840606
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Connor, J. W., Hastie, R. J. & Taylor, J. B. 1971 Shear, periodicity, and plasma ballooning modes. Phys. Rev. Lett. 40 (17), 1464–1465.Google Scholar
Dimits, A. M., Bateman, G., Beer, M. A., Cohen, B. I., Dorland, W., Hammett, G. W., Kim, C., Kinsey, J. E., Kotschenreuther, M., Kritz, A. H. et al. 2000 Comparisons and physics basis of tokamak transport models and turbulence simulations. Phys. Plasmas 7 (3), 969.Google Scholar
Helander, P. 2014 Microstability of magnetically confined electron–positron plasmas. Phys. Rev. Lett. 113 (3), 1–4.Google Scholar
Helander, P. 2017 Available energy and ground states of collisionless plasmas. J. Plasma Phys. 83 (04), 715830401.Google Scholar
Helander, P. & Connor, J. W. 2016 Gyrokinetic stability theory of electron–positron plasmas. J. Plasma Phys. 82 (3), 1–13.Google Scholar
Helander, P., Proll, J. H. E. & Plunk, G. G. 2013 Collisionless microinstabilities in stellarators. I. Analytical theory of trapped-particle modes. Phys. Plasmas 20 (12), 122505.Google Scholar
Horn-Stanja, J., Biancalani, A., Bottino, A., Mishchenko, A. & Sunn Pedersen, T.2018 Linear gyrokinetic studies with orb5 en route to pair plasmas. Submitted to Phys. Plasmas.Google Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. N. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7 (5), 1904–1910.Google Scholar
Mishchenko, A., Plunk, G. G. & Helander, P. 2018a Electrostatic stability of electron–positron plasmas in dipole geometry. J. Plasma Phys. 84 (02), 905840201.Google Scholar
Mishchenko, A., Zocco, A., Helander, P. & Könies, A. 2018b Gyrokinetic stability of electron–positron–ion plasmas. J. Plasma Phys. 84 (01), 905840116.Google Scholar
Pedersen, S. T., Boozer, A. H., Dorland, W., Kremer, J. P. & Schmitt, R. 2003 Prospects for the creation of positron–electron plasmas in a non-neutral stellarator. J. Phys. B 36 (5), 1029–1039.Google Scholar
Pedersen, S. T., Danielson, J. R., Hugenschmidt, C., Marx, G., Sarasola, X., Schauer, F., Schweikhard, L., Surko, C. M. & Winkler, E. 2012 Plans for the creation and studies of electron–positron plasmas in a stellarator. New J. Phys. 14 (3), 035010.Google Scholar
Saitoh, H., Stanja, J., Stenson, E. V., Hergenhahn, U., Niemann, H., Pedersen, T. S., Stoneking, M. R., Piochacz, C. & Hugenschmidt, C. 2015 Efficient injection of an intense positron beam into a dipole magnetic field. New J. Phys. 17 (10), 103038.Google Scholar
Zocco, A. 2017 Slab magnetised non-relativistic low-beta electron–positron plasmas: collisionless heating, linear waves and reconnecting instabilities. J. Plasma Phys. 83 (06), 715830602.Google Scholar