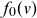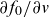Landau damping for non-Maxwellian distribution functions

Abstract

Landau damping is one of the cornerstones of plasma physics. Based on the initial-value approach adopted by Landau in his original derivation of Landau damping, we examine the solutions of the linear Vlasov–Poisson system for different equilibrium distribution functions $f_0(v)$, going beyond the traditional focus on the root with largest imaginary part and investigating the full set of roots that the dispersion relation of the system generally admits. Specifically, we provide analytical insights into the number and the structure of the roots for entire and meromorphic functions $f_0(v)$, such as Maxwellian and $\kappa$ distributions, we discuss the potential issues related to the redefinition of $\partial{f}_0/\partial{v}$ as a complex variable function and we show how different sigmoids affect the root structure associated with non-meromorphic cut-off distribution functions. Finally, based on the comparison of the several root structures considered, we wonder if the multiple roots might hint at a deeper understanding of the Landau damping phenomenon.

1. Introduction

Landau damping is the paradigmatic example of kinetic effects in plasma physics. It consists of an interaction mechanism between waves and particles in a collisionless plasma, which converts wave energy into particle kinetic energy. The damping phenomenon was mathematically predicted by Lev Landau in 1946 for one-dimensional electrostatic oscillations and it was later identified in essentially all other modes of collective oscillations in plasmas. Through the years it extended well beyond plasma physics: analogous mechanisms have also been recognised in various branches of physics (e.g. astrophysics, hydrodynamics, high-energy physics) and other sciences (e.g. biology) (Vekstein 1998; Ryutov 1999), and the mathematical proof of the survival of Landau damping in the nonlinear setting provided ‘an unexpected bridge between three of the most famous paradoxical statements from classical mechanics in the twentieth century: Landau damping, KAM theory, and the echo experiment’ (Villani 2010).

In this work, we study Landau damping for the linear Vlasov–Poisson system (LVP) in the context of Landau’s original initial-value approach (Landau 1946). Under the assumption of a uniform and static ion background, LVP describes high-frequency one-dimensional electrostatic oscillations and it is given as

(1.1) \begin{align} \frac {\partial {f_{1}(x,v,t)}}{\partial {t}} + v \frac {\partial {f_{1}(x,v,t)}}{\partial {x}} - \frac {e}{m} E(x,t) \frac {\partial {f_{0}(v)}}{\partial {v}} = 0, \\[-18pt] \nonumber \end{align}

(1.2) \begin{align} \frac {\partial {E}(x,t)}{\partial {x}} = -\frac {e n_0}{\epsilon _0}\int \mathrm {d}v f_{1}(x,v,t), \end{align}

where $E(x,t)$ is the electric field, $e$ is the elementary charge, $m$ is the electron mass and $n_0$ is the equilibrium ion–electron number density. The function $f(x,v,t)=f_0(v)+f_1(x,v,t)$ corresponds to the electron velocity distribution integrated over $v_y$ and $v_z$ , split into an equilibrium part $f_{0}(v)$ and a perturbation part $f_{1}(x,v,t)$ . By following Landau and by assuming that $f_0(v)$ is a Maxwellian distribution function, the evolution of the Fourier-transformed electric field, $E(k,t)=\int _{-\infty }^{\infty }E(x,t){\rm e}^{-ikx}{\rm d}x$ , is given as a linear combination of initial-value modes:

(1.3) \begin{align} E(k,t) = \sum _n A_n {\rm e}^{-ip_nt}, \end{align}

where $p_n=\omega _n+i\gamma _n$ are the roots, with $\gamma _n\lt 0$ , of the dispersion relation

(1.4) \begin{align} k^2 - {\omega ^2_p \left [ \int _{-\infty }^{\infty } \frac {\partial {f_{0}(v)}/\partial {v}}{v - p/k} \mathrm {d}v + 2i \pi \frac {\partial f_0}{\partial v}(p/k) \right ]} = 0, \end{align}

and $\omega _p=\sqrt {e^2n_0/m_e\epsilon _0}$ is the plasma frequency.

The present work is based on two interesting aspects related to the dispersion relation of (1.4): the total number of roots $p_n$ and the generic evaluation of $\partial f_0/\partial v$ at the complex value $p/k$ .

Firstly, (1.4) generally admits more than one root. However, in the literature it is common to focus solely on the root $p_n$ with the largest imaginary part $\gamma _n$ , as this root dominates the long-time behaviour of (1.3). The aim of the present work is then to explore the multiple solutions that LVP admits and investigate how the structure of solutions is affected by equilibrium distribution functions $f_0(v)$ that are not Maxwellian, such as the examples of figure 1.

Figure 1. One-dimensional distribution functions. See later sections for analytical definitions.

Secondly, velocity distribution functions and their derivatives are generally defined as real-valued functions in the real variable $v\in \mathbb {R}$ . Nonetheless, the term $\partial f_0/\partial v(p/k)$ in (1.4), with $p/k$ a complex number, requires the redefinition of $\partial f_0/\partial v$ as a complex variable function. For some distribution functions, e.g. Maxwellian and $\kappa$ distributions (with integer $\kappa$ ), the redefinition can be performed naturally by simply replacing the real variable $v\in \mathbb {R}$ with a complex one $z\in \mathbb {C}$ . For others, e.g. incomplete distributions and $\kappa$ distributions with non-integer $\kappa$ , the redefinition can be performed neither continuously nor uniquely. The distinction between the two groups of distribution functions, for which the term $\partial f_0/\partial v(p/k)$ is either well- or ill-defined, leads us to organise this work as follows.

In § 2 we follow the literature and provide the necessary mathematical background. In addition, we discuss how the assumption of Maxwellian $f_0(v)$ can be relaxed and how the dispersion relation of (1.4) can be considered valid for non-Maxwellian distributions.

In § 3 we deal with the first group of distribution functions. Specifically, we show a simple argument to establish the number of roots, we describe analytically the strongly damped roots in the Maxwellian $f_0(v)$ case and we advance a tentative explanation for the physical meaning of the different solutions of LVP.

In § 4 we consider the second class of distribution functions. We mainly focus on the case of distribution functions with compact support, also known as cut-off distributions, that are defined through the Heaviside step function $H(v)$ and that, as an example, are relevant for the description of non-thermal ions in fusion plasmas. We notice that different definitions are possible for the dispersion relation, and although this leads to the same $E$ field evolution, we wonder how such ambiguity arises. To investigate this, we employ different sigmoid functions to replace the Heaviside step function and we observe how different root structures arise. In addition, based on the physical interpretation of Landau damping as an average synchronisation mechanism (Escande et al. 2018, § 3.2), we determine which sigmoid is to be preferred. Lastly, we briefly take two other cases into account, namely the slowing-down distribution function and $\kappa$ distributions with non-integer $\kappa$ parameters, and show the respective root structures.

In summary, the present work corresponds to an investigation of the multiple and strongly damped roots of LVP. While on the one hand, such an investigation is motivated by the belief that these roots might relate to an enrichment in the understanding of Landau damping, on the other hand a more practical motivation is connected to the study of electromagnetic oscillations in tokamak plasmas, which can be described as the roots of a linear electromagnetic dispersion relation (Lauber 2013, equation (20)) containing terms similar to the left-hand side of (1.1). Specifically, as shown in Girardo (2015) (see figures 4.2 and 4.8 therein) for energetic-particle-driven geodesic acoustic modes (EGAMs), strongly damped roots of the electromagnetic dispersion relation can be destabilised by the introduction of a fast particle population (e.g. bump on tail distribution) and can potentially impact the plasma dynamics (e.g. via quasi-linear theory). Hence the need of examining and rigorously defining such roots for distribution functions that can occur in a tokamak plasma (e.g. Maxwellian, slowing down). Then, because of the similarities in the formulation of the problems, we adopt the electrostatic LVP as a simplified case to gain insights that can be later translated to the electromagnetic setting.

As a final comment, it is worth mentioning that the plots of the dispersion relation in the form of (1.4) are the main investigation tool of this paper and, as analytical expressions are not always available, we heavily resort to the numerical scheme from Xie (2013), which allows the numerical evaluation of the integral in (1.4) for arbitrary distribution functions $f_0(v)$ .

2. The LVP: solution for $E(k,t)$ and assumptions on $f_0(v)$

The approach adopted in Landau (1946) consists of applying a Laplace transform in time and a Fourier transform in space to LVP. After some algebra, the Laplace–Fourier transform of the electric field $\tilde {E}_{\textit {UHP}}(p,k)$ can be analytically defined in the upper half-plane (UHP; $\mathrm {Im}(p)\gt 0$ ) as

(2.1) \begin{align} \tilde {E}_{\textit {UHP}}(k,p) = \frac {G_{\textit {UHP}}(k,p)}{\epsilon _{\textit {UHP}}(k,p)}, \end{align}

where $G_{\textit {UHP}}$ and $\epsilon _{\textit {UHP}}$ correspond to

(2.2) \begin{align} \begin{split} G_{\textit {UHP}}(k,p) &= \frac {e}{k\epsilon _0}\int _{-\infty }^{\infty }\frac {\tilde {f}_{1}(t=0,k,v)}{p-kv}\mathrm {d}v,\,\,\,\,\,\,\,\,\, \mathrm {Im}(p)\gt 0, \\ \epsilon _{\textit {UHP}}(k,p) &= {1+\frac {e^2}{k\epsilon _0m}\int _{-\infty }^{\infty } \frac {f^{\prime}_0(v)}{p-kv} \mathrm {d}v}, \,\,\, \mathrm {Im}(p)\gt 0. \end{split} \end{align}

Here, $\tilde {f}_{1}(t=0,k,v)$ is the Fourier transform of the distribution function perturbation at time $t=0$ , $f_1(t=0,x,v)$ . Moreover, we note that from now on the $\partial /\partial v$ operator is replaced for clarity of notation by a prime mark $^{\prime}$ , e.g. $\partial {f_{0}(v)}/\partial {v} \to f^{\prime}_0(v)$ .

In its most general form, the solution for the electric field is then given as the inverse Laplace transform of $\tilde {E}_{\textit {UHP}}(k,p)$ :

(2.3) \begin{align} E(k,t) = \frac {1}{2\pi } \int _{i\sigma -\infty }^{i\sigma +\infty } {\rm e}^{-ipt} \tilde {E}_{\textit {UHP}}(k,p)\,\mathrm {d}p, \end{align}

where the $p$ -integration is performed on the horizontal line $p=i\sigma + t$ , with $t\in [{-}\infty, \infty ]$ . Here $\sigma$ is defined such that $\sigma \gt \text {Max}_n\left \{0,\mathrm {Im}{(p_n)}\right \}$ , i.e. the integration path lies in the UHP and above all the UHP singularities $\{p_n\}_{\textit {UHP}}$ of $\tilde {E}_{\textit {UHP}}(p,k)$ . We remark that $\tilde {E}_{\textit {UHP}}(k,p)$ has been defined only in the UHP, as $\tilde {G}_{\textit {UHP}}(k,p)$ and $\tilde {\epsilon }_{\textit {UHP}}(k,p)$ are discontinuous as $\mathrm {Im}(p)\to 0^{\pm }$ and are ill-defined when $\mathrm {Im}(p)=0$ .

Although it can already be considered the final solution for the electric field, (2.3) can be more conveniently recast into the sum of initial-value modes by exploiting the residue theorem. The integration contour over $p=i\sigma + t$ is then closed with an infinite-radius semicircle in the lower half-plane (LHP) and the functions $G_{\textit {UHP}}$ and $\epsilon _{\textit {UHP}}$ are analytically extended to $\mathrm {Im}(p)\leqslant 0$ by replacing the integral $\int _{-\infty }^{\infty }$ with the Landau integration contour $\int _{LC}$ . Specifically, for a generic function $F(z)$ , the integral $\int _{-\infty }^{\infty }\mathrm {d}vF(v)/(v-z)$ becomes ¹

(2.4) \begin{align} Z(z,F)=\int _{LC} {\frac {F(v)}{v-z}\mathrm {d}v} = \begin{cases} \int _{-\infty }^{\infty } \frac {F\left (v\right )}{v-z} \mathrm {d}v, & \mathrm {Im}(z)\gt 0, \\[3pt] \mathrm {P.V.}\!\! \int _{-\infty }^{\infty } \frac {F\left (v\right )}{v-z} \mathrm {d}v+i\pi F(z), & \mathrm {Im}(z)=0, \\[3pt] \int _{-\infty }^{\infty } \frac {F\left (v\right )}{v-z} \mathrm {d}v+2 i\pi F(z), & \mathrm {Im}(z)\lt 0.\end{cases} \end{align}

Thus, $G_{\textit {UHP}}$ and $\epsilon _{\textit {UHP}}$ are extended as

(2.5) \begin{align} \begin{split} G(k,p) &= \frac {e}{k\epsilon _0}\int _{LC}\frac {f_{1}(k,v,t=0)}{p-kv}\mathrm {d}v, \\ \epsilon (k,p) &= {1+\frac {e^2}{k\epsilon _0m}\int _{LC}\frac {f^{\prime}_0(v)}{p-kv} \mathrm {d}v} = 1 - \frac {\omega ^2_p}{k^2} Z(p/k,f^{\prime}_0), \end{split} \end{align}

and $\tilde {E}(k,p)$ is redefined as

(2.6) \begin{align} \tilde {E}(k,p) = \frac {G(k,p)}{\epsilon (k,p)}. \end{align}

If $f_1(k,v,t=0)$ and $f_0(z)$ are entire functions in the complex variable $z$ , $G$ and $\epsilon$ are also entire functions, and the only singularities of $\tilde {E}(p,k)$ are the zeros of $\epsilon (k,p)$ . Applying the residue theorem then yields

(2.7) \begin{align} E(k,t) = \frac {1}{2\pi } \int _{i\sigma -\infty }^{i\sigma +\infty } {\rm e}^{-ipt} \frac {G(k,p)}{\epsilon (k,p)} \mathrm {d}p = - i \sum _n {\rm e}^{-ip_nt} \frac {G(k,p_n)}{\partial \epsilon / \partial p|_{p_n}}, \end{align}

with $p_n$ denoting the roots of the dispersion relation $\epsilon (k,p_n)=0$ . Moreover, it can be shown that if $f_0(v)$ has only one maximum, no roots with $\gamma _n\ge 0$ are to be expected, and the dispersion relation assumes the form of (1.4) (Stix 1962).

Let us now comment on Landau’s analyticity requirements for ${f}_{1}(k,z,t=0)$ and $f_{0}(z)$ in the complex $z$ variable, namely their analyticity across the whole complex plane (i.e. entire functions). If the final solution is to be expressed as the sum of exponentials with frequencies exclusively given as roots of the dielectric function, the assumption on ${f}_{1}(k,z,t=0)$ cannot be abandoned. Abandoning this assumption introduces $G(p,k)$ singularities that the residue theorem must account for. In the present work, we follow Landau and we always keep ${f}_{1}(k,z,t=0)$ entire. For a discussion on ’non-Landau solutions’ induced by disregarding the requirement on ${f}_{1}(k,z,t=0)$ , see Belmont et al. (2008).

On the other hand, (2.7) remains valid if the assumption on $f_0(z)$ is relaxed by simply requiring it to be meromorphic, i.e. a complex function that is analytical on the whole complex plane except for a set of isolated points. In this case, the singularities of $f_0$ do not pose any issue for the residue theorem because an isolated $\epsilon (p,k)$ singularity translates to an analyticity point of $1/\epsilon (p,k)$ . As we show in the next section, singularities of $f_0(z)$ are also meaningful as they can be regarded as the generators of the roots of the dispersion relation. Entire and meromorphic functions $f_0(z)$ correspond to the aforementioned first group of distribution functions $f_0(v)$ , which admit a straightforward complex redefinition and are dealt with in the next section.

Additionally, distribution functions $f_0(v)$ that cannot be redefined continuously in the whole complex plane are associated with some $f_0(z)$ that is neither entire nor meromorphic. The function $f_0(z)$ , and consequently $\tilde {E}(k,p)$ , thus feature non-isolated discontinuity points that the residue theorem must avoid. As shown in Twiss (1952) and Weitzner (1963), the residue theorem has to circumvent such discontinuities and (2.3) has to be corrected as

(2.8) \begin{align} \begin{split} E(k,t) &= \frac {1}{2\pi }\int _{i\sigma -\infty }^{i\sigma +\infty } {\rm e}^{-ipt} \tilde {E}(k,p)\mathrm {d}p \\ &= -i\sum _n\text {Res}\left \{{\rm e}^{-ip_nt} \tilde {E}(k,p_n)\right \} - \frac {1}{2\pi }\int _{\varGamma _D}{\rm e}^{-ipt} \tilde {E}(k,p)\mathrm {d}p. \end{split} \end{align}

where $\varGamma _D$ indicates the contour around the non-isolated discontinuity of the Laplace transformed electric field, $\tilde {E}(k,p)$ , and $p_n$ are the roots of the dispersion relation $\epsilon (k,p_n)=0$ . An interesting feature of (2.8) is that, despite leading to the same electric field $E(k,t)$ , its right-hand side can be defined in multiple ways. Section 4 goes into more details of such a feature.

3. Distribution functions with unique complex definition

In this section we consider the case of equilibrium distribution functions $f_0(v)$ that can be uniquely redefined as an entire or meromorphic complex-variable function, $f_0(z)$ . Notable examples are the well-known Maxwellian distribution

\begin{equation*}f_{Max}(v) = \frac {1}{\sqrt {\pi v_t^2}}{\rm e}^{-v^2/v_t^2},\end{equation*}

and $\kappa$ distributions with integer $\kappa$ , of which we consider the one-dimensional version from Lima et al. (2000),

(3.1) \begin{align} f_{\kappa }(v) = A_{\kappa }\left (1+\frac {v^2}{\kappa v_t^2}\right )^{-\kappa }, \end{align}

where $A_\kappa$ is the normalisation constant and $v_t$ is defined as $\sqrt {2T/m}$ , with $T$ corresponding to a generic temperature parameter. While the Maxwellian distribution represents the standard equilibrium state of statistical physics and all plasma physics, $\kappa$ distributions are the non-thermal stationary states of non-extensive statistical mechanics, and it has been shown experimentally that they well describe low-collisionality plasma systems, such as the solar wind and the solar corona (Lazar & Fichtner 2021).

3.1. Number of solutions

If we assume an entire or meromorphic equilibrium distribution function $f_0(z)$ that admits only one maximum on the real axis, all the roots of the dispersion relation $p_n=\omega _n + i\gamma _n$ lie in the LHP and the dispersion relation $\epsilon (k,p)=0$ is written as

(3.2) \begin{align} k^2 = \omega _p^2 \int _{-\infty }^{\infty }{\frac {f^{\prime}_0(v)}{v-z}\mathrm {d}v} +2i \pi \omega _p^2 f^{\prime}_0(z), \quad \mathrm {Im}(z)\lt 0, \end{align}

with $z=p/k$ . In the limit $k\to \infty$ , the integral term can be neglected and (3.2) becomes

(3.3) \begin{align} \frac {k^2}{\omega _p^2} \approx 2 i \pi f^{\prime}_0(z). \end{align}

As $k$ can be arbitrarily large, the previous equality can be satisfied only if its right-hand side can also be made arbitrarily large. In other words, $z$ must belong to a sufficiently small neighbourhood of a singularity point of $f^{\prime}_0(z)$ . Let us then assume that $z$ belongs to a small neighbourhood of $z_0$ , a singularity point of order $n$ in the LHP. By representing $z-z_0$ as $R{\rm e}^{i\theta }$ , we can approximate $f^{\prime}_0(z)$ as

(3.4) \begin{align} f^{\prime}_0(z) \approx \frac {C(z_0){\rm e}^{i\alpha (z_0)}}{R^n {\rm e}^{in\theta }}, \end{align}

where $C(z_0){\rm e}^{i\alpha (z_0)}$ is the $n$ -order coefficient of the Laurent series expansion. Plugging (3.4) into (3.3) and taking the absolute value and the phase of the resulting equation yield

(3.5) \begin{align} \begin{cases} k^2 = \frac {\pi \omega _p^2 C}{R^n} \rightarrow R_n = \sqrt [n]{\frac {\pi \omega _p^2 C}{k^2}},\\ 2m\pi = \frac {\pi }{2} +\alpha -n\theta \rightarrow \theta _{n,m} = -\frac {2m\pi }{n} + \frac {\pi /2 + \alpha }{n}. \end{cases} \end{align}

Hence, given $n$ (and $k$ ), the approximate solutions $z_n$ can be expressed as $z_0+R_n{\rm e}^{i\theta {n,m}}$ . We then conclude that, as $k\to \infty$ , each singularity $z_s$ in the LHP, of order $n_s$ , is generating $n_s$ roots $p_s$ of the dispersion relation of (3.2). Moreover, such roots are distributed symmetrically around the singularity $z_0$ .

As an example, figure 2 shows the roots for a $\kappa =2$ distribution $f_{\kappa =2}$ for two different $k$ values. In agreement with our previous considerations, the plot on the left depicts the short-wavelength limit $k\to \infty$ . It exhibits three roots, as many as the order of the $f^{\prime}_{\kappa =2}$ singularity, distributed symmetrically around the singularity $z_0=-i\sqrt {\kappa v_t^2}$ . Moreover, the intersections between the red circle and the half-lines $m = i$ give the location of the roots according to (3.5).

Figure 2. Dispersion relation roots for the $f_0=f_{\kappa =2}$ case, with $v_t=\sqrt 2$ . Here $k$ is rescaled to the dimensionless $k^{\prime}=k\lambda _D$ , with $\lambda _D=v_t/(\omega _p\sqrt 2)$ . Left: $k^{\prime}=10$ case and comparison with (3.5). Right: $k^{\prime}=0.1$ case.

In the right-hand plot, figure 2 shows instead the opposite long-wavelength limit $k\to 0$ . Compared with the left-hand plot, symmetry is lost because of the non-negligible contribution of the integral term, and the roots are here found in regions where $\partial \epsilon /\partial p$ has different values. Recalling that $\partial \epsilon /\partial p$ appears in the linear combination coefficients of (2.7), we deduce that the two small damping roots, in regions of smaller $|\partial \epsilon /\partial p|$ , dominate the electric field evolution and that the contribution from the third root is suppressed. This behaviour is compatible with the $k\to 0$ limit of Landau (1946), for which two stable roots oscillating at the plasma frequency are predicted.

As a final comment we remark that we demonstrated how many roots are to be expected only in the case $k\to \infty$ . However, even if not supported by a rigorous mathematical proof, observing the root structure at different $\kappa$ and $k$ seems to suggest that the number of solutions for distribution functions with a single singularity point in the $\text{LHP}$ does not depend on the wave vector $k$ .

3.2. Maxwellian

As regards the Maxwellian distribution, we firstly remark that $f_{Max}(v)$ is naturally associated with the entire function $f_{Max}(z)$ by simply replacing $v\in \mathbb {R}$ with $z\in \mathbb {C}$ . In other words, $f_{Max}(z)$ has no singularities at finite real and imaginary parts. Still, it diverges as $\mathrm {Im}(z)$ goes to $-\infty$ so that, in a broader sense, the Maxwellian features a singularity of order infinity at $\mathrm {Im}(z)=-\infty$ . Based on the previous discussion about singularities, we then expect infinite solutions to the associated dispersion relation. To describe these solutions analytically, ² we neglect the integral term of (3.2) ( $k\to \infty$ limit) and we plug in $f_{Max}(z)$ , so that

(3.6) \begin{align} k^2 \approx 2i\pi \omega _p^2 f^{\prime}_{Max}(z), \end{align}

and, with $z$ expressed in polar form $R{\rm e}^{i\theta }$ ,

(3.7) \begin{align} k^2\lambda ^2_D = -2i\sqrt \pi \frac {R{\rm e}^{i\theta }}{v_t} \exp \!\left ({{-}\frac {R^2{\rm e}^{i\theta }}{v_t^2}}\right ). \end{align}

Here, we defined $\lambda ^2_D$ as the ratio $2v^2_t/\omega ^2_p$ . By setting $k^{\prime2}=k^2\lambda ^2_D$ and by taking the absolute value and the phase of the previous equation, we obtain the system

(3.8) \begin{align} \begin{cases} k^{\prime2} = 2\sqrt \pi \frac {R}{v_t} \exp \!\left ({{-}\frac {R^2\cos {2\theta }}{v_t^2}}\right ), \\ 2\pi m = \frac {3\pi }{2} + \theta - \frac {R^2\sin {2\theta }}{v_t^2}. \end{cases} \end{align}

The first equation of the system in the limit of large $R/v_t$ yields

(3.9) \begin{align} k^2 = 2\sqrt \pi \frac {R}{v_t} \exp \left ({-\frac {R^2\cos {2\theta }}{v_t^2}}\right ) \propto \delta (2\theta - \pi /2 - \pi n) \end{align}

and implies that $\theta = ({\pi }/{4}) + ({\pi }/{2}) n$ . As we are considering only the LHP, the solutions for $\theta$ are $\theta = \left \{-({\pi }/{4}),-({3}/{4})\pi \right \}$ (with $n=-1,-2$ ), and by substituting these values into the second equation of (3.8), we determine

(3.10) \begin{align} 2\pi m + \frac {3\pi }{4} = \frac {R^2}{v_t^2} \to \frac {R}{v_t} =\sqrt {\pm 2\pi m + \frac {3\pi }{4}}, \end{align}

where the plus and minus signs correspond, respectively, to $\theta = -{\pi }/{4}$ and $\theta = -{3}/{4}$ . It is clear that, due to the assumption of large $R/v_t$ needed for (3.9), the solution for $R/v_t$ becomes more accurate as $m$ grows. The correctness of (3.10) in the limit $R\to \infty$ is depicted in figure 3.

Figure 3. Maxwellian multi-roots, solutions of the dispersion relation $k^{\prime2}-v_t^2Z(z,f^{\prime}_{Max})/{}2=0$ , with thermal velocity $v_t=0.1$ and wave vector $k^{\prime}=10$ . The analytical expression of (3.10) is also represented.

3.3. From $\kappa$ to Maxwellian

The typical feature of the ’Maxwellian’ LVP is that its dispersion relation admits infinite roots. Mathematically, the Maxwellian root structure can be straightforwardly connected to the root structure for the $\kappa$ distribution case by simply observing the limit

(3.11) \begin{align} f_{\kappa }(z) = A_{\kappa }\left (1+\frac {v^2}{\kappa v_t^2}\right )^{-\kappa } \xrightarrow {\kappa \to \infty } f_{M} = \frac {1}{\sqrt {\pi }v_t}{\rm e}^{-v^2/v_t^2}. \end{align}

Specifically, as shown in figure 4, the Maxwellian root structure can be interpreted as the root structure induced by an equilibrium $\kappa$ distribution with $\kappa$ that goes to infinity and with the singularity $-i\sqrt {\kappa v_t^2}$ that moves towards $\mathrm {Im}(z)=-\infty$ .

Figure 4. Roots for $\kappa$ distributions approaching a Maxwellian. Left: $f_0=f_{\kappa =8}$ ; centre: $f_0=f_{\kappa =80}$ ; right: $f_0=f_{\kappa =\infty }=f_{Max}$ . Parameters used: $v_t=\sqrt {2}$ , $k^{\prime}=1$ .

If the singularity argument sheds light on how the roots of the LVP dispersion relation arise from a purely mathematical point of view, we wonder if a deeper physical meaning can be associated with the number and the structure of LVP solutions or, in other words, if there exists a physical property related to the equilibrium distribution function that determines the number of roots of the LVP dispersion relation.

A tentative and speculative interpretation is suggested by considering the more precise definition of $\kappa$ distributions in the framework of non-extensive statistical mechanics. In particular, given an $N$ -particle system with $f$ degrees of freedom ( $f=ND$ stands for the product of $N$ and the single particle degrees of freedom, $D$ ), the $f$ -dimensional $\kappa$ distribution function is introduced (Livadiotis & McComas 2011) as

(3.12) \begin{align} f_{\kappa _0}\left (\vec {v}\right )\propto \left (1+ \frac {1}{\kappa _0 v_t^2} \sum _{i=1}^f v_{i}^2\right )^{-\kappa _0-1-f/2}, \end{align}

where $\vec {v}$ denotes the $f$ -dimensional velocity vector, with components $\{v_0,v_1,\ldots, v_f\}$ , and $\kappa _0$ is the invariant $\kappa$ index. Consequently, the one-dimensional distribution function for the single degree of freedom is obtained by marginalising $f_N$ over the $f-1$ degrees of freedom, and the more precise version of (3.1) is then given as

(3.13) \begin{align} f_{\kappa _0}(v) \propto \left (1+\frac {v^2}{\kappa _0 v_t^2}\right )^{-\kappa _0 -3/2}. \end{align}

The same Livadiotis & McComas (2011) proves that $\kappa _0$ represents the thermodynamic distance from the Maxwellian thermal equilibrium and captures the correlation $\rho$ between the degrees of freedom of the system through the expression

\begin{equation*} \rho (\kappa _0) = \frac {1/2}{1/2 + \kappa _0}, \end{equation*}

where the correlation $\rho$ between two generic velocity degrees of freedom, $v_i$ and $v_j$ , is defined as

\begin{equation*} \rho (\kappa _0 )=\frac {\langle v_i^2 \cdot v_j^2\rangle -\langle v_i^2 \rangle \cdot \langle v_j^2 \rangle }{\sqrt { \langle v_i^4 \rangle - \langle v_i^2 \rangle ^2} \sqrt { \langle v_j^4 \rangle - \langle v_j^2 \rangle ^2}}, \end{equation*}

with the angle brackets denoting averaging over the distribution function $f_N$ .

Hence, as $\kappa _0$ increases, larger collisionality destroys correlation, and in the limit $\kappa _0\to \infty$ , the null-correlation Maxwellian distribution is retained.

Recalling that the number of LVP roots corresponds to the order of the $f^{\prime}_0(z)$ LHP singularity ( $\kappa _0+1/2$ for the $f_0=f_{\kappa _0}$ case ³ ), we are consequently tempted to hypothesise a connection between the number of roots and the system correlation so that a stronger (weaker) correlation implies fewer (more) roots and a reduced (increased) ’freedom of movement’ of the system.

4. Non-unique analytical continuation

For other interesting cases, the complex redefinition $f_0(v)\to f_0(z)$ cannot be performed as straightforwardly as in the previous section. The main notable examples involve distribution functions that feature an empty interval $\mathcal {I}$ such that $f_0(v\in \mathcal {I})\approx 0$ :

1. (i) Incomplete distributions. In laboratory plasmas, in the presence of potential barriers, such as sheaths near material walls or probes, a trapped-passing boundary is created. As a consequence, at the edge of an absorbing wall sheath the passing interval of the electron distribution will be empty.

2. (ii) Slowing-down distribution. Fast ions, such as $3.5$ MeV α $\alpha$ -particles and NBI beams in fusion plasmas, because of their high energy compared with the background and because of the low intra-species collisionality, do not thermalise to the Maxwellian state. Instead, they slow down via collisions with the background plasma to a stable distribution known as a slowing-down distribution, where $f_0(|v|\gt v_c)\approx 0$ , with $v_c$ standing for the fast species injection velocity (Gaffey 1976).

In both cases, if we neglect the energy dispersion, the empty intervals can be modelled by means of the Heaviside function $H(v)$ , which is responsible for the problematic complex redefinition.

A further example, not related to the Heaviside function, corresponds to $\kappa$ distribution with non-integer $\kappa$ . In fact, when $\kappa$ is a non-integer, the complex distribution function $f_0(z)$ becomes multi-valued and branch cuts are introduced.

In the following, we focus on the case of cut-off distributions, which exemplify the issues connected to the Heaviside function, and we later briefly mention the specific case of slowing-down and non-integer $\kappa$ distributions.

4.1. Cut-off distributions

We formally define cut-off distributions as

(4.1) \begin{align} f_{CO}(v) = \begin{cases} F_0(v) & \text {if } |v| \leqslant v_c, \\ 0 & \text {otherwise}, \end{cases} \end{align}

and we conveniently express them in terms of the Heaviside function $H(v)$ :

(4.2) \begin{align} f_{CO}(v) = H(v+v_c) \cdot F_0(v) \cdot H(-v+v_c) = F_0(v) W_{v_c}(v) . \end{align}

Here, we introduce $W_{v_c}(v)$ as the symmetric ’window’ function with cut-off velocity $v_c$ , representing the product of two Heaviside functions. For simplicity, we further assume that $F_0(v)$ is a symmetric real-valued function with a single maximum and a unique definition in the LHP. ⁴ The derivative $f^{\prime}_{CO}(v)$ is then given by

(4.3) \begin{align} f^{\prime}_{CO}(v) = F^{\prime}_0(v) W_{v_c}(v)+F_0(v) \left [\delta (v+v_c) - \delta (v-v_c)\right ]. \end{align}

By considering the definition from (2.4) of the ’Landau integral’ with $F(v)=f^{\prime}_{CO}(v)$ ,

(4.4) \begin{align} Z(z,f^{\prime}_{CO}) = \int _{LC}\frac {f^{\prime}_{CO}(v)}{p-kv} \mathrm {d}v, \end{align}

we realise that $Z(z,f^{\prime}_{CO})$ remains consistent and uniquely defined in the UHP and on the real axis, but not in the LHP.

4.1.1. Upper half-plane and real axis

Given the assumptions on $F_0$ , the same arguments from Stix (1962) can be applied and unstable solutions with $\mathrm {Im}(z)\gt 0$ can be excluded. On the other hand, on the real axis the dispersion relation becomes

(4.5) \begin{align} \frac {k^2}{\omega _p^2}= \mathrm {P.V.}\!\!\int _{-v_c}^{v_c}{\frac {F^{\prime}_0(v)}{v-z}\mathrm {d}v} + F_0(v_c) \frac {2v_c}{z^2-v_c^2} + \pi i F^{\prime}_0(v) W_{v_c}(v), \end{align}

and similarly to Weitzner (1963) we can show that if $F_0(v_c)\neq 0$ a stable solution exists for any value of $k$ , provided $|\mathrm {Re}(z)|\gt v_c$ .

The real-axis solution remains consistent with the argument that singularities generate solutions, as the singularity point of $f^{\prime}_{CO}$ at $z=\pm v_c$ is responsible for such a stable root. In addition, the physical interpretation in terms of the standard resonant interaction mechanism is also straightforward. Compact support implies that no particles at velocities larger than $v_c$ are present. Hence, when the wave phase velocity is greater than $v_c$ there is no interacting particle, and the wave propagates without damping.

Since unstable solutions are absent, the stable solution dominates the long-time limit. Nonetheless, to examine the full-time evolution of $E(k,t)$ , the LHP must be investigated and $f^{\prime}_{CO}(z)$ must be defined.

4.1.2. Lower half-plane

In the LHP, the formal definition of $Z(z,f^{\prime})$ for cut-off distributions is

(4.6) \begin{align} Z_{\textit {LHP}}(z,f^{\prime}_{CO}) = \int _{-\infty }^{\infty }{\frac {F^{\prime}_0(v) W_{v_c}(v)}{v-z}\mathrm {d}v} + 2\pi i F^{\prime}_0(z)W_{v_c}(z) + F_0(v_c)\frac {2v_c}{z^2-v_c^2}. \end{align}

While $F^{\prime}_0(z)$ is generally well-defined, $W_{v_c}(z)$ is not. Since there is no unique way to define $W_{v_c}(z)$ , we introduce three different possible definitions, among infinitely many, for the ’window’ function:

(4.7) \begin{align} \begin{split} W_{v_c,0}(z) &= 0,\\ W_{v_c,1}(z) &= H(v_c-|\mathrm {Re}(z)|),\\ W_{v_c,2}(z) &= 1. \end{split} \end{align}

This leads to three different definitions for $Z(z,f^{\prime}_{CO})$ in the LHP:

(4.8) \begin{align} \begin{split} Z_{\textit {LHP},0}(z,f^{\prime}_{CO}) &= \int _{-v_c}^{v_c}{\frac {F^{\prime}_0(v)}{v-z}\mathrm {d}v} + F_0(v_c) \frac {2v_c}{z^2-v_c^2},\\ Z_{\textit {LHP},1}(z,f^{\prime}_0) &= \int _{-v_c}^{v_c}{\frac {F^{\prime}_{CO}(v)}{v-z}\mathrm {d}v} + 2\pi i F^{\prime}_0(z)H(v_c-|\mathrm {Re}(z)|) + F_0(v_c) \frac {2v_c}{z^2-v_c^2},\\ Z_{\textit {LHP},2}(z,f^{\prime}_{CO}) &= \int _{-v_c}^{v_c}{\frac {F^{\prime}_0(v)}{v-z}\mathrm {d}v} + 2\pi i F^{\prime}_0(z) + F_0(v_c) \frac {2v_c}{z^2-v_c^2}, \end{split} \end{align}

and to three different dispersion relations and associated roots, as depicted in figure 5.

Figure 5. Root structures for different LHP definitions of $f_{CO}$ . The white lines represent the discontinuity of the different $Z_{i}(z)$ . The support function $F_0$ is a $\kappa =1$ distribution $f_{\kappa =1}$ , with $v_t=\sqrt {2}$ .

Despite different root structures, (2.8) guarantees that the electric field evolution does not depend on the specific definition $W_{v_c}(z)$ . The key point is to observe that extending the window function $W_{v_c}(z)$ into the LHP leads to non-isolated points of discontinuity for $Z(z,f^{\prime}_0)$ and $E(p,k)$ . When applying the residue theorem, such discontinuities must be circumvented as exemplified in figure 6, and lead to the additional integral term. Nevertheless, we notice that:

1. (i) In the original Landau treatment, as per (2.7), the $E$ field solution could be entirely decomposed into the sum of residues, i.e. initial-value modes. On the contrary, when $f^{\prime}_0(z)$ is not continuous, this is not true as an integral contribution around $\varGamma _D$ remains. Thus, the whole point of applying the residue theorem to conveniently express the inverse Laplace transform as a sum of residues no longer holds. We then wonder if the integral contribution $\varGamma _D$ can be expressed, at least approximately, as the sum of initial-value modes.

2. (ii) Although the final result is the same, multiple equivalent descriptions are possible in the LHP. Again, we wonder if the LHP extension is a pure mathematical artefact or whether it might hide some physical meaning.

Figure 6. Discontinuities generated by the different definitions for the ’window’ function, $W_{v_c,0}$ , $W_{v_c,1}$ and $W_{v_c,2}$ , and the associated contour $\varGamma _D$ needed for (2.8).

To tackle these aspects, we include energy dispersion in the equilibrium distribution function by smoothing the Heaviside function by means of sigmoid functions.

4.2. Smooth cut-off distributions

Because of energy dispersion, a cut-off distribution more realistically entails a high-energy tail rather than being sharply cut off at $v=v_c$ . We model such energy dispersion in two possible ways: with a logistic sigmoid:

(4.9) \begin{align} \sigma _{\log, \alpha }(v) = \frac {1}{1+{\rm e}^{-v/\alpha }} \xrightarrow {\quad \alpha \to 0 \quad } H(v) = \begin{cases}1 &v\gt 0, \\ 1/2 &v=0, \\ 0 &v\lt 0, \end{cases} \end{align}

and an error function sigmoid:

(4.10) \begin{align} \sigma _{\textrm {erf},\alpha }(v) = \frac {1 + \textrm {erf}(v/\alpha )}{2} \xrightarrow {\quad \alpha \to 0 \quad } H(v) = \begin{cases}1 &v\gt 0, \\ 1/2 &v=0, \\ 0 &v\lt 0, \end{cases} \end{align}

that both converge (point-wise) to the Heaviside function in the limit $\alpha \to 0$ (figure 7). The parameter $\alpha$ represents the steepness of the sigmoid and the error function is defined as $\textrm {erf}(z)=2/\sqrt {\pi }\int _{0}^{z}\exp {(-t^2)}{\rm d}t$ . While the choice of the logistic sigmoid is not based on any a priori physical derivation and it was simply included in the discussion because of the simple analytical expression, the error function sigmoid appears analytically as one of the terms describing the energy dispersion for the fast-ion slowing-down distribution function (Gaffey 1976).

Figure 7. Logistic and error function sigmoids. The $\alpha$ parameters are chosen in order to approximately overlap the sigmoids.

Both sigmoids are well defined as complex variable functions when $v\in \mathbb {R}$ is replaced by $z\in \mathbb {C}$ but, despite a similar real-axis behaviour and the same real-axis limit, they behave quite differently in the complex plane, as shown in figure 8. Specifically, $\sigma _{\log, \alpha }(z)$ converges point-wise to a function that corresponds almost everywhere to $H(\mathrm {Re}(z))$ :

(4.11) \begin{align} \lim _{\alpha \to 0}\left [{\frac {1}{1+{\rm e}^{-z/\alpha }}}\right ] = \begin{cases} 1 +i0 &x\gt 0\\ 0 +i0&x\lt 0\\ \frac {1}{2}+i0 &x=0,y\neq -\pi \alpha -2\pi m\alpha \\ \infty + i 0 &x=0,y=-\pi \alpha -2\pi m\alpha . \end{cases} \end{align}

On the other hand, observing the following decomposition of the error function $\textrm {erf}(z/\alpha )$ :

(4.12) \begin{align} \textrm {erf}(z/\alpha ) = \frac {2}{\sqrt {\pi }}\int _{0}^{x/\alpha }{\rm e}^{-t^2}\mathrm {d}t + \frac {2i}{\sqrt {\pi }}\int _{0}^{y/\alpha }{\rm e}^{-(x/\alpha )^2+s^2}{\rm e}^{-2ixs/\alpha }\mathrm {d}s \end{align}

yields that in the region $\mathrm {Re}(z)^2-\mathrm {Im}(z)^2\gt 0$ , $\sigma _{\textrm {erf},\alpha }(z)$ converges to $1$ if $\mathrm {Re}(z)\gt 0$ and to $0$ if $\mathrm {Re}(z)\lt 0$ , and outside the region $\mathrm {Re}(z)^2-\mathrm {Im}(z)^2\gt 0$ no convergence is guaranteed.

Figure 8. Real part of the complex variable logistic ( $\sigma _{\log, \alpha }(z)$ , left) and error function ( $\sigma _{\textrm {erf},\alpha }(z)$ , right) sigmoid. The $\alpha$ parameters are chosen so that the two sigmoids approximately overlap on the real axis. The singularities of $\sigma _{\log, \alpha }(z)$ are also highlighted.

By employing the sigmoid functions just introduced, we can then define ’smooth’ cut-off distribution functions:

(4.13) \begin{align} f_{\textrm {erf},\alpha }(z) = \sigma _{\textrm {erf},\alpha }(z+v_c) \cdot F_0(z) \cdot \sigma _{\textrm {erf},\alpha }(-z+v_c) \end{align}

and

(4.14) \begin{align} f_{\log, \alpha }(z) = \sigma _{\log, \alpha }(z+v_c) \cdot F_0(z) \cdot \sigma _{\log, \alpha }(-z+v_c), \end{align}

and observe the impact of different sigmoids on the solution of LVP.

Firstly, with the dominated convergence theorem, it can be proven that the LVP solution $E_{\alpha }(k,t)$ with $f_0=f_{\textrm {erf},\alpha }$ or $f_0=f_{\log, \alpha }$ converges to the same solution $E(k,t)$ with $f_0=f_{CO}$ . Even if trivial in appearance, this fact ensures the good behaviour of the LVP solution in the limit $\alpha \to 0$ , regardless of the chosen sigmoid.

Secondly, as both $f_{\textrm {erf},\alpha }(z)$ and $f_{\log, \alpha }(z)$ fall into the entire/meromorphic functions class, the electric field solution can be entirely expressed as the sum of residue contributions, as per (2.7). However, because of the different behaviour of the sigmoids in the complex plane, the root structure will look significantly different, depending on the sigmoid.

As a specific example, figure 9 shows the root structures for smooth cut-off distributions $f_{\log, \alpha }(z)$ for different $\alpha$ values, with the $\kappa =1$ distribution as support function $F_0$ . By applying the concepts of § 3, the following comments can be made:

• In both plots, we can recognise the left-most root as one of the two roots generated by the singularity of the support function derivative $F^{\prime}_0=f^{\prime}_{\kappa =1}$ .

• In both plots, the remaining roots are generated by the logistic sigmoid. According to (4.9), the singularities of $\sigma ^{\prime}_{\log }$ are located at $\mathrm {Re}{(z\pm v_c)}=0$ and $\mathrm {Im}(z)=-\alpha \pi (1+2m)$ . Moreover, as can be easily seen by Taylor expanding $1/(1+{\rm e}^{(-x/\alpha )})^2$ , such singularities are of order 2 and generate two roots each.

• Among the sigmoid roots, the smallest damping one resembles the stable root of the $f_{CO,\kappa =1}(z)$ case, shown in figure 5.

• As $\alpha$ decreases, in agreement with the expression $\mathrm {Im}(z)=-\alpha \pi (1+2m)$ , singularities and roots get denser and closer to $\mathrm {Re}(z)=v_c$ . We reckon a similarity between the root structure of $f_{\log, \alpha }(z)$ in the limit $\alpha \to 0$ and the root structure from $Z_1(f^{\prime}_{CO})$ , discontinuous at $\mathrm {Re}{(z)}=\pm v_c$ (centre plot in figure 5).

Figure 9. Root structures for the smooth cut-off distribution $f_{\log,\alpha }$ with $\alpha =0.1$ (left) and $\alpha =0.02$ (right). The support function $F_0$ is a $\kappa =1$ distribution with $v_t=\sqrt {2}$ and the cut-off is at $v_c=2$ .

As a term of comparison, figure 10 depicts the root structure of the same cut-off $\kappa =1$ distribution smoothed out by the error function sigmoid $\sigma _{\textrm {erf},\alpha }$ , with the $\alpha$ parameters chosen so that $\sigma _{\textrm {erf},\alpha }(v)$ have qualitatively the same steepness as $\sigma _{\log, \alpha }(v)$ used for figure 9. The root structure is evidently dissimilar.

• The root generated by the singularity of $F^{\prime}_0=f^{\prime}_{\kappa =1}$ is no longer observable.

• The sigmoid function generates the remaining roots. In particular, as the derivative $\sigma _{\textrm {erf},\alpha }$ is proportional to ${\rm e}^{-z^2}$ , we notice a root structure similar to the Maxwellian case of figure 3. Moreover, the nearly stable root can still be spotted.

• In the limit $\alpha \to 0$ , the sigmoid singularities become denser. However, they do not approach the same discontinuous structure as in the logistic case. Here, the sigmoid structure approaches a structure that is discontinuous in the LHP along the directions $\theta =\{-\pi /4,-3\pi /4\}$ , suggesting a new definition for the complex Heaviside function, i.e.

  (4.15) \begin{align} H(z) = H(\mathrm {Im}(z)^2-\mathrm {Re}(z)^2) = \begin{cases}1 &\mathrm {Im}(z)^2\gt \mathrm {Re}(z)^2, \\ 0 &\mathrm {Im}(z)^2\lt \mathrm {Re}(z)^2. \end{cases} \end{align}

Figure 10. Root structures for the smooth cut-off distribution $f_{\textrm {erf},\alpha }$ , $\alpha =0.1$ (left) and $\alpha =0.02$ (right). The support function $F_0(v)$ is a $\kappa =1$ distribution with $v_t=\sqrt {2}$ and the cut-off is at $v_c=2$ .

Based on the plots above, we are then led to conclude that the discontinuous dielectric functions associated with the Heaviside functions can be interpreted as the limiting case of ’sigmoid-smoothed’ distribution functions. In particular, different sigmoid functions lead to different discontinuous dielectric functions, and the ambiguity in the complex definition of the Heaviside function can be connected to the multiple sigmoids one could use to replace $H(v)$ . Moreover, we observe that by employing sigmoid functions, the discontinuity contribution $\varGamma _D$ from (2.8) can be approximated and decomposed into the (infinite) sum of modes generated by the sigmoid function. As the sigmoid gets steeper, the infinite number of such solutions get denser and phase mix to yield the power-law decay of the $\varGamma _D$ integral, previously shown by Hudson (1962).

4.2.1. A privileged sigmoid?

Although the two different sigmoid functions can be considered mathematically equivalent as they lead in the limit $\alpha \to 0$ to the same electric field evolution, we wonder if one of them can be preferred in terms of its physical interpretation.

According to the common interpretation of Landau damping as a resonance effect, damping occurs because of the resonant interaction between the electric field component $\propto {\rm e}^{\gamma t -i\omega t}$ and the particles with velocity $v\approx \omega /k$ . Therefore, given a generic equilibrium distribution $f_0(v)=F_0(v)$ that features the set of roots $\mathcal {A}=\{p_n\}$ , we expect the associated cut-off distribution $f_{CO}(v)=F_0(v) H(|v|\lt v_c)$ to yield the set $\mathcal {B}=\{p_n|v_c\gt |\mathrm {Re}{(p_n)}/k|\}$ in addition to the aforementioned stable solution. That is, the roots associated with the support function $F_0$ are roots for the cut-off distribution case if they resonate with the non-empty region of $f_{CO}$ , i.e. $|\mathrm {Re}{(p_n)}/k|\lt v_c$ . Consequently, the natural way of defining the complex Heaviside function according to the resonance interpretation would be $H(z)=H(\mathrm {Re}(z))$ , as in the definition $W_{v_c,1}$ . When accounting for energy dispersion, the sigmoid $\sigma _{\log }$ is then preferred over $\sigma _{\textrm {erf}}$ because of the limit

\begin{equation*} \sigma _{\log, \alpha }(v)\to H(\mathrm {Re}(z)), \quad \text{a.e.}, \end{equation*}

and because the roots that $\sigma _{\log, \alpha }(z)$ introduces are all located in the region $\omega /k\approx v_c$ , where the steep gradient acts as the sink of the wave damping process.

However, the resonance interpretation is not fully accurate. Instead, Landau damping is more precisely described as a non-resonant mechanism that originates from the average synchronisation of particles with respect to the wave, and given a mode of complex frequency $\omega +i\gamma$ , the particles for which the synchronisation is maximised are those whose velocity $v$ satisfies the condition $|kv-\omega |\approx |\gamma |$ (Escande et al. 2018). As illustrated in figure 10, the roots generated by the error function sigmoid are approximately located along the half-lines defined by $|v_c-\mathrm {Re(z)}|\approx \pm \mathrm {Im(z)}$ (originating from $z=v_c$ and directed along $\theta =\{-\pi /4,-3\pi /4\}$ ), and by recalling that $z=(\omega +i\gamma )/k$ , we immediately associate the half-lines with the maximum synchronisation condition. In other words, the real frequency $\omega$ and the damping $\gamma$ of the roots are compatible with the fact that the maximum synchronisation occurs in the region $v\approx v_c$ where the sigmoid is located. Therefore, we conclude that because of the compatibility with the more precise non-resonant interpretation of Landau damping, the error function sigmoid corresponds to the more physical way of describing the energy dispersion for a cut-off distribution.

4.3. Slowing-down and non-integer $\kappa$ distributions

So far, we have focused on the non-analytical features of the LVP dispersion relation induced by the Heaviside function. However, other cases exist where the complex variable distribution features non-isolated points of discontinuities that are not determined by the Heaviside function. For example, the one-dimensional slowing-down distribution can be defined as in Xie (2013):

(4.16) \begin{align} f_{SD}(v) = N(v_t,v_c) \frac {1}{|v|^3+v_t^3}W_{v_c}(v), \end{align}

where $v_t$ is a generic parameter, $v_c$ is the cut-off (injection) velocity and $N$ is the normalisation constant. While the same discussion from the previous section applies for $W_{v_c}(v)$ , the additional non-analytical feature of $f_{SD}$ is related to the absolute value of $v$ , which emerges from the approximation $v\approx v_c$ needed to simplify the expression for $f_{SD}$ (Gaffey 1976). Nevertheless, the discontinuity induced in the complex plane by $|v|$ can be removed by noticing that

\begin{equation*} |v|=v\cdot \text {sign}(v)=v\cdot [2H(v)-1] \end{equation*}

and by simply approximating $H(v)$ with a sigmoid function. The left-hand plot of figure 11 shows the roots for $f_{SD,\alpha, \beta }$ , corresponding to the ’smoothed’ version of $f_{SD}$ :

(4.17) \begin{align} f_{SD}(v) = \sigma _{\alpha }(z+v_c) \cdot \frac {N(v_t,v_c)}{v^3\cdot [2\sigma _{\beta }(v)-1]^3+v_t^3} \cdot \sigma _{\alpha }(-z+v_c), \end{align}

with $\sigma _{\alpha }$ and $\sigma _{\beta }$ identifying two generic sigmoid functions with respective steepness parameter $\alpha$ and $\beta$ . While the $\mathrm {Re}(z)\sim v_c$ roots relate to the $W_{v_c}$ -induced discontinuity observed in the previous section, the $\mathrm {Re}(z)\sim 0$ roots relate to the $|v|$ -induced discontinuity. Despite arguing in the previous section that the error function sigmoid is to be preferred from a physical point of view, figure 11 shows the case with a logistic sigmoid chosen for both $\sigma _{\alpha }$ and $\sigma _{\beta }$ simply because it provides a more understandable plot.

Figure 11. Left: dispersion relation roots for the ’smooth’ slowing-down distribution. Logistic sigmoids are used, with steepness parameter $\alpha =\beta =0.1$ . Other parameters: $v_t=\sqrt {2}$ , $v_c=3$ , $k^{\prime}=1$ . Right: imaginary part of the function $Z(z,f^{\prime}_{\kappa =4.2})$ . The white line represents the discontinuity.

Another example worth mentioning corresponds to $\kappa$ distributions, defined in (3.1), with non-integer $\kappa$ , whose non-analytical feature arises because non-integer powers of complex numbers are multi-valued and require the introduction of branch cuts. Namely, different discontinuous LHP definitions are possible depending on the chosen orientation of the branch cut. However, while the discontinuities induced by the Heaviside function and by the absolute value of $v$ can be removed by employing sigmoid functions, we did not find a way to eliminate the discontinuity induced by the non-integer power branch cut (right-hand plot of figure 11), hence implying that the integral term on the right-hand side of (2.8) would have to be retained. Moreover, a physical explanation for the branch cut discontinuity and the different possible definitions for the complex variable non-integer $\kappa$ distribution is yet to be found.

5. Conclusions and outlook

The present work focused on the full set of solutions of the LVP à la Landau. We discussed how the multiple roots of the dispersion relation are generated, and for the case of entire/meromorphic functions we showed that the number of roots in the $k\to \infty$ limit is equal to the order of the singularity of the equilibrium distribution function derivative $f^{\prime}_0(z)$ . In the same limit $k\to \infty$ we also provided analytical formulas to describe the roots for general meromorphic and Maxwellian distribution functions. On the other hand, for the case of the cut-off distribution function, we showed that the non-uniqueness of the associated LHP description can be related to the different possible ways of describing the energy dispersion and that the sigmoid functions allow the decomposition of the LHP discontinuities of the dispersion relation into a set of damped roots. We also noticed that among the considered logistic and error function sigmoids, the error function sigmoid is more physically accurate by virtue of the consistency with the average synchronisation mechanism at the origin of Landau damping. Finally, we mentioned the case of non-integer $\kappa$ -distributions, for which the ambiguity of the LHP description has not been resolved.

On a different note, as symbolised by briefly considering the slowing-down distribution, the various aspects discussed in this paper lay the ground for studying the influence of non-Maxwellian distributions on the more complex electromagnetic case in tokamak geometry, mentioned in the introduction. Some preliminary work, which examines the non-analytical features of the electromagnetic dispersion relation induced by different equilibrium distribution functions, is presented in Stucchi (2024), while a more comprehensive analysis on the structure of the electromagnetic roots is left for future work. In particular, it would be interesting to inspect in more detail, for both the electrostatic and the electromagnetic case, the destabilisation of damped roots described by Girardo (2015, Chapter 4), as this could be potentially used as an experimental means to investigate the properties of EGAMs and to probe the root structures in the LHP.

At a deeper level, the analysis carried out made us ponder whether an improved understanding of the Landau damping phenomenon might hide behind the strongly damped roots, specifically in terms of some physical property of the equilibrium distribution function that could explain the number and the structure of roots. While remarking on the need for further and more rigorous investigation, we speculated about a possible connection between Landau damping and the correlation among the degrees of freedom of the system.

Furthermore, it is worth noticing that throughout the present work we assumed that the plasma under consideration could be described by a continuous (or piece-wise continuous) distribution function $f_0(v)$ . However, in some cases, e.g. when $f_0(v)$ approaches zero, such as in the presence of steep sigmoid functions, this assumption might be debatable and an $N$ -body discrete description on the model of Escande et al. (2018, § 5.5) might be more accurate. For future work, we hence believe that analysing the root structures presented here in terms of the $N$ -body approach can be an interesting starting point, in particular by checking if the multiple roots can be retained and connected to some property in the dynamics of the $N$ particles.