Hostname: page-component-cc8bf7c57-xrnlw Total loading time: 0 Render date: 2024-12-12T02:15:40.000Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic ballooning modes in tokamaks and stellarators

Part of: PLA 17th European Fusion Theory Conference Focus on Fusion

Published online by Cambridge University Press:  11 December 2018

K. Aleynikova ,
A. Zocco Open the ORCID record for A. Zocco [Opens in a new window] ,
P. Xanthopoulos ,
P. Helander  and
C. Nührenberg
K. Aleynikova*
Affiliation:
Max-Planck-Institut für Plasmaphysik, EURATOM Association, Greifswald, Germany Moscow Institute of Physics and Technology, Dolgoprudny, Russian Federation
A. Zocco
Affiliation:
Max-Planck-Institut für Plasmaphysik, EURATOM Association, Greifswald, Germany
P. Xanthopoulos
Affiliation:
Max-Planck-Institut für Plasmaphysik, EURATOM Association, Greifswald, Germany
P. Helander
Affiliation:
Max-Planck-Institut für Plasmaphysik, EURATOM Association, Greifswald, Germany
C. Nührenberg
Affiliation:
Max-Planck-Institut für Plasmaphysik, EURATOM Association, Greifswald, Germany
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

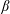Kinetic ballooning modes (KBMs) are investigated by means of linear electromagnetic gyrokinetic (GK) simulations in the stellarator Wendelstein 7-X (W7-X), for high-$\unicode[STIX]{x1D6FD}$ plasmas, where 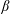$\unicode[STIX]{x1D6FD}$ is the ratio of thermal to magnetic plasma pressure. The analysis shows suppression of ion-temperature-gradient (ITG) and trapped particle modes (TEM) by finite-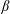$\unicode[STIX]{x1D6FD}$ effects and destabilization of KBMs at high 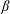$\unicode[STIX]{x1D6FD}$. The results are compared with a generic tokamak case. We show that, for large pressure gradients, the frequency of KBMs evaluated by the GENE code is in agreement with the analytical prediction of the diamagnetic modification of the ideal magnetohydrodynamic limit in W7-X general geometry. Thresholds for destabilization of the KBM are predicted for different W7-X equilibrium configurations. We discuss the relation of these thresholds to the ideal magnetohydrodynamic (MHD) stability properties of the corresponding equilibria.

Keywords

fusion plasmaplasma instabilitiesplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 6 , December 2018 , 745840602
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

de Aguilera, A. M., Castejón, F., Ascasíbar, E., Blanco, E., De la Cal, E., Hidalgo, C., Liu, B., López-Fraguas, A., Medina, F., Ochando, M. A. et al. 2015 Magnetic well scan and confinement in the TJ-II stellarator. Nucl. Fusion 55 (11), 113014.Google Scholar
Aleynikova, K. & Zocco, A. 2017 Quantitative study of kinetic ballooning mode theory in simple geometry. Phys. Plasmas 24 (9), 092106.Google Scholar
Baumgaertel, J., Belli, E., Dorland, W., Guttenfelder, W., Hammett, G., Mikkelsen, D., Rewoldt, G., Tang, W. & Xanthopoulos, P. 2011 Simulating gyrokinetic microinstabilities in stellarator geometry with GS2. Phys. Plasmas 18 (12), 122301.Google Scholar
Beer, M. A., Cowley, S. C. & Hammett, G. 1995 Field-aligned coordinates for nonlinear simulations of tokamak turbulence. Phys. Plasmas 2 (7), 2687–2700.Google Scholar
Belli, E. & Candy, J. 2010 Fully electromagnetic gyrokinetic eigenmode analysis of high-beta shaped plasmas. Phys. Plasmas 17 (11), 112314.Google Scholar
Biancalani, A., Bottino, A., Briguglio, S., Könies, A., Lauber, P., Mishchenko, A., Poli, E., Scott, B. & Zonca, F. 2016 Linear gyrokinetic particle-in-cell simulations of Alfvén instabilities in tokamaks. Phys. Plasmas 23 (1), 012108.Google Scholar
Boozer, A. H. 1980 Enhanced transport in tokamaks due to toroidal ripple. Phys. Fluids 23 (11), 2283–2290.Google Scholar
Connor, J., Hastie, R. & Taylor, J. 1978 Shear, periodicity, and plasma ballooning modes. Phys. Rev. Lett. 40 (6), 396.Google Scholar
Dannert, T. & Jenko, F. 2005 Gyrokinetic simulation of collisionless trapped-electron mode turbulence. Phys. Plasmas 12 (7), 072309.Google Scholar
Diallo, A., Hughes, J., Greenwald, M., LaBombard, B., Davis, E., Baek, S., Theiler, C., Snyder, P., Canik, J., Walk, J. et al. 2014 Observation of edge instability limiting the pedestal growth in tokamak plasmas. Phys. Rev. Lett. 112 (11), 115001.Google Scholar
Dickinson, D., Roach, C., Skipp, J. & Wilson, H. 2014 Structure of micro-instabilities in tokamak plasmas: stiff transport or plasma eruptions? Phys. Plasmas 21 (1), 010702.Google Scholar
Dorland, W., Jenko, F., Kotschenreuther, M. & Rogers, B. 2000 Electron temperature gradient turbulence. Phys. Rev. Lett. 85 (26), 5579.Google Scholar
Goerler, T., Lapillonne, X., Brunner, S., Dannert, T., Jenko, F., Merz, F. & Told, D. 2011 The global version of the gyrokinetic turbulence code GENE. J. Comput. Phys. 230 (18), 7053–7071.Google Scholar
Groebner, R., Chang, C., Hughes, J., Maingi, R., Snyder, P., Xu, X., Boedo, J., Boyle, D., Callen, J., Canik, J. et al. 2013 Improved understanding of physics processes in pedestal structure, leading to improved predictive capability for ITER. Nucl. Fusion 53 (9), 093024.Google Scholar
Groebner, R., Snyder, P., Osborne, T., Leonard, A., Rhodes, T., Zeng, L., Unterberg, E. A., Yan, Z., McKee, G., Lasnier, C. et al. 2010 Limits to the H-mode pedestal pressure gradient in DIII-D. Nucl. Fusion 50 (6), 064002.Google Scholar
Hastie, R. & Hesketh, K. 1981 Kinetic modifications to the MHD ballooning mode. Nucl. Fusion 21 (6), 651.Google Scholar
Helander, P., Beidler, C., Bird, T., Drevlak, M., Feng, Y., Hatzky, R., Jenko, F., Kleiber, R., Proll, J., Turkin, Y. et al. 2012 Stellarator and tokamak plasmas: a comparison. Plasma Phys. Control. Fusion 54 (12), 124009.Google Scholar
Hirshman, S., Merkel, P. & van Rij, W. I. 1986 Three-dimensional free boundary calculations using a spectral Green’s function method. Comput. Phys. Commun. 43 (1), 143–155.Google Scholar
Ishizawa, A., Maeyama, S., Watanabe, T.-H., Sugama, H. & Nakajima, N. 2015 Electromagnetic gyrokinetic simulation of turbulence in torus plasmas. J. Plasma Phys. 81 (2), doi:10.1017/S0022377815000100.Google Scholar
Jenko, F., Dorland, W., Kotschenreuther, M. & Rogers, B. 2000 Electron temperature gradient driven turbulence. Phys. Plasmas 7 (5), 1904–1910.Google Scholar
Kleiber, R. & Scott, B. 2005 Fluid simulations of edge turbulence for stellarators and axisymmetric configurations. Phys. Plasmas 12 (10), 102507.Google Scholar
Kornilov, V., Kleiber, R., Hatzky, R., Villard, L. & Jost, G. 2004 Gyrokinetic global three-dimensional simulations of linear ion-temperature-gradient modes in Wendelstein 7-X. Phys. Plasmas 11 (6), 3196–3202.Google Scholar
Kotschenreuther, M. 1986 Compressibility effects on ideal and kinetic ballooning modes and elimination of finite Larmor radius stabilization. Phys. Fluids 29 (9), 2898–2913.Google Scholar
Kotschenreuther, M., Rewoldt, G. & Tang, W. 1995 Comparison of initial value and eigenvalue codes for kinetic toroidal plasma instabilities. Comput. Phys. Commun. 88 (2–3), 128–140.Google Scholar
Mishchenko, A., Borchardt, M., Cole, M., Hatzky, R., Fehér, T., Kleiber, R., Könies, A. & Zocco, A. 2015 Global linear gyrokinetic particle-in-cell simulations including electromagnetic effects in shaped plasmas. Nucl. Fusion 55 (5), 053006.Google Scholar
Mishchenko, A., Hatzky, R. & Könies, A. 2008 Global particle-in-cell simulations of Alfvénic modes. Phys. Plasmas 15 (11), 112106.Google Scholar
Nührenberg, C. 2016 Free-boundary ideal MHD stability of W7-X divertor equilibria. Nucl. Fusion 56 (7), 076010.Google Scholar
Nührenberg, J., Bondeson, A., Zille, R., Sindoni, E. & Troyon, F. 1988 Equilibrium and stability of low-shear stellarators. In Theory of Fusion Plasmas, pp. 3–23. Theory of Fusion Plasmas.Google Scholar
Proll, J., Mynick, H., Xanthopoulos, P., Lazerson, S. & Faber, B. 2015 Tem turbulence optimisation in stellarators. Plasma Phys. Control. Fusion 58 (1), 014006.Google Scholar
Proll, J. H. E., Helander, P., Connor, J. W. & Plunk, G. 2012 Resilience of quasi-isodynamic stellarators against trapped-particle instabilities. Phys. Rev. Lett. 108 (24), 245002.Google Scholar
Proll, J. H. E., Xanthopoulos, P. & Helander, P. 2013 Collisionless microinstabilities in stellarators. II. Numerical simulations. Phys. Plasmas 20 (12), 122506.Google Scholar
Pueschel, M. J., Kammerer, M. & Jenko, F. 2008 Gyrokinetic turbulence simulations at high plasma beta. Phys. Plasmas 15 (10), 102310.Google Scholar
Riemann, J., Kleiber, R. & Borchardt, M. 2016 Effects of radial electric fields on linear ITG instabilities in W7-X and LHD. Plasma Phys. Control. Fusion 58 (7), 074001.Google Scholar
Roberts, K. & Taylor, J. 1962 Magnetohydrodynamic equations for finite Larmor radius. Phys. Rev. Lett. 8 (5), 197.Google Scholar
Rogers, B. N., Zhu, B. & Francisquez, M. 2018 Gyrokinetic theory of slab universal modes and the non-existence of the gradient drift coupling (GDC) instability. Phys. Plasmas 25 (5), 052115.Google Scholar
Rosenbluth, M. & Sloan, M. 1971 Finite- $\unicode[STIX]{x1D6FD}$ stabilization of the collisionless trapped particle instability. Phys. Fluids 14 (8), 1725–1741.Google Scholar
Snyder, P., Groebner, R., Hughes, J., Osborne, T., Beurskens, M., Leonard, A., Wilson, H. & Xu, X. 2011 A first-principles predictive model of the pedestal height and width: development, testing and iter optimization with the EPED model. Nucl. Fusion 51 (10), 103016.Google Scholar
Tang, W., Connor, J. & Hastie, R. 1980 Kinetic-ballooning-mode theory in general geometry. Nucl. Fusion 20 (11), 1439.Google Scholar
Tsai, S.-T. & Chen, L. 1993 Theory of kinetic ballooning modes excited by energetic particles in tokamaks. Phys. Fluids B 5 (9), 3284–3290.Google Scholar
Xanthopoulos, P., Cooper, W. A., Jenko, F., Turkin, Y., Runov, A. & Geiger, J. 2009 A geometry interface for gyrokinetic microturbulence investigations in toroidal configurations. Phys. Plasmas 16 (8), 082303.Google Scholar
Xanthopoulos, P. & Jenko, F. 2007 Gyrokinetic analysis of linear microinstabilities for the stellarator Wendelstein 7-X. Phys. Plasmas 14 (4), 042501.Google Scholar
Xanthopoulos, P., Merz, F., Görler, T. & Jenko, F. 2007 Nonlinear gyrokinetic simulations of ion-temperature-gradient turbulence for the optimized Wendelstein 7-X stellarator. Phys. Rev. Lett. 99 (3), 035002.Google Scholar
Zocco, A., Helander, P. & Connor, J. 2015 Magnetic compressibility and ion-temperature-gradient-driven microinstabilities in magnetically confined plasmas. Plasma Phys. Control. Fusion 57 (8), 085003.Google Scholar
Zocco, A., Xanthopoulos, P., Doerk, H., Connor, J. & Helander, P. 2018 Threshold for the destabilisation of the ion-temperature-gradient mode in magnetically confined toroidal plasmas. J. Plasma Phys. 84 (1).Google Scholar