Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T19:55:53.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Ion-acoustic wave instability driven by drifting electrons in a generalized Lorentzian distribution

Published online by Cambridge University Press:  13 March 2009

Zhaoyue Meng ,
Richard M. Thorne  and
Danny Summers
Zhaoyue Meng
Affiliation:
Department of Atmospheric Sciences, University of California at Los Angeles, Los Angeles, California 90024–1565, U.S.A.
Richard M. Thorne
Affiliation:
Department of Atmospheric Sciences, University of California at Los Angeles, Los Angeles, California 90024–1565, U.S.A.
Danny Summers
Affiliation:
Department of Mathematics and Statistics, Memorial University of Newfoundland, St John's, Newfoundland, CanadaA1C 5S7
Get access Rights & Permissions [Opens in a new window]

Abstract

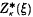A generalized Lorentzian (kappa) particle distribution function is useful for modelling plasma distributions with a high-energy tail that typically occur in space. The modified plasma dispersion function is employed to study the instability of ion-acoustic waves driven by electron drift in a hot isotropic unmagnetized plasma modelled by a kappa distribution. The real and imaginary parts of the wave frequency ω0 + ιγ are obtained as functions of the normalized wavenumber kλD, where λD is the electron Debye length. Marginal stability conditions for instability are obtained for different ion-to-electron temperature ratios. The results for a kappa distribution are compared with the classical results for a Maxwellian. In all cases studied the ion-acoustic waves are strongly damped at short wavelengths, kλD ≫ 1, but they can be destabilized at long wavelengths. The instability for both the kappa and Maxwellian distributions can be quenched by increasing the ion-electron temperature ratio Ti/Te. However, both the marginally unstable electron drift velocities and the growth rates of unstable waves can differ significantly between a generalized Lorentzian and a Maxwellian plasma; these differences are also influenced by the value of Ti/Te.

Type
Research Article
Information
Journal of Plasma Physics , Volume 47 , Issue 3 , June 1992 , pp. 445 - 464
Copyright
Copyright © Cambridge University Press 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham-Shrauner, B. & Feldman, W. C. 1977 J. Plasma Phys. 17, 123.CrossRefGoogle Scholar
Abraham-Shrauner, B., Asbridge, J. R., Bame, S. J. & Feldman, W. C. 1979 J. Geophys. Res. 84, 553.CrossRefGoogle Scholar
Anderson, R. R., Parks, G. K., Eastman, T. E., Gurnett, D. A. & Frank, L. A. 1981 J. Geophys. Res. 86, 4493.Google Scholar
Armstrong, T. P., Paonessa, M. T., Bell, E. V. & Krimigis, S. M. 1983 J. Geophys. Res. 88, 8893.Google Scholar
Chen, F. F. 1984 Introduction to Plasma Physics and Controlled Fusion. Plenum.CrossRefGoogle Scholar
Fried, B. D. & Conte, S. P. 1961 The Plasma Dispersion Function. Academic.Google Scholar
Greenwald, R. A., Weiss, W., Nielson, E. & Thomson, N. R. 1978 Radio Sci. 13, 1021.Google Scholar
Haldoupis, C. & Schlegel, K. 1990 J. Geophys. Res. 95, 18989.Google Scholar
Hasegawa, A., Mima, K. & Duong-Van, M. 1985 Phys. Rev. Lett. 54, 2608.Google Scholar
Ichimaru, S. 1973 Basic Principles of Plasma Physics: A Statistical Approach. Benjamin.Google Scholar
Jackson, E. A. 1960 Phys. Fluids 3, 786.Google Scholar
Kindel, J. M. & Kennel, C. F. 1971 J. Geophys. Res. 76, 3055.CrossRefGoogle Scholar
Landau, L. D. 1946 J. Phys. USSR 10, 25.Google Scholar
Nielson, E. & Schlegel, K. 1983 J. Geophys. Res. 88, 5745.CrossRefGoogle Scholar
Nielson, E. & Schlegel, K. 1985 J. Geophys. Res. 90, 3498.CrossRefGoogle Scholar
Scarf, F. L., Crook, G. M. & Fredricks, R. W. 1965 J. Geophys. Res. 70, 3045.Google Scholar
Summers, D. & Thorne, R. M. 1991 Phys. Fluids B 3, 1835.Google Scholar
Swanson, D. G. 1989 Plasma Waves. Academic.CrossRefGoogle Scholar
Swift, D. W. 1965 J. Geophys. Res. 70, 3061.Google Scholar
Thokne, R. M. & Summers, D. 1991 Phys. Fluids B 3, 2117.Google Scholar
Tsurutani, B. & Rodriguez, P. 1981 J. Geophys. Res. 86, 4319.Google Scholar
Vasyliunas, V. M. 1968 J. Geophys. Res. 73, 2839.Google Scholar
Williams, D. J., Mitchell, D. G. & Christon, S. P. 1988 Geophys. Res. Lett. 15, 303.Google Scholar