No CrossRef data available.
Article contents
Investigation of the collisionless plasmoid instability based on gyrofluid and gyrokinetic integrated approach
Published online by Cambridge University Press: 11 July 2023
Abstract
In this work, the development of two-dimensional current sheets with respect to tearing modes, in collisionless plasmas with a strong guide field, is analysed. During their nonlinear evolution, these thin current sheets can become unstable to the formation of plasmoids, which allows the magnetic reconnection process to reach high reconnection rates. We carry out a detailed study of the effect of a finite $\beta _e$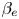 , which also implies finite electron Larmor radius effects, on the collisionless plasmoid instability. This study is conducted through a comparison of gyrofluid and gyrokinetic simulations. The comparison shows in general a good capability of the gyrofluid models in predicting the plasmoid instability observed with gyrokinetic simulations. We show that the effects of $\beta _e$
, which also implies finite electron Larmor radius effects, on the collisionless plasmoid instability. This study is conducted through a comparison of gyrofluid and gyrokinetic simulations. The comparison shows in general a good capability of the gyrofluid models in predicting the plasmoid instability observed with gyrokinetic simulations. We show that the effects of $\beta _e$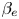 promotes the plasmoid growth. The effect of the closure applied during the derivation of the gyrofluid model is also studied through the comparison among the variations of the different contributions to the total energy.
promotes the plasmoid growth. The effect of the closure applied during the derivation of the gyrofluid model is also studied through the comparison among the variations of the different contributions to the total energy.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press



