Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-25T06:14:32.719Z Has data issue: false hasContentIssue false
  • English
  • Français

Integrodifferential models of electron transport for negative ion sources

Part of: Complex Plasma Phenomena

Published online by Cambridge University Press:  08 October 2015

Marco Cavenago
Marco Cavenago*
Affiliation:
INFN-LNL, Lab. Nazionali Legnaro, Accelerator division, v.le dell’Università n. 2, I-35020, Legnaro (PD), Italy
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Thanks to the presence of a transverse magnetic flux density (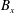$B_{x}$ and 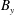$B_{y}$ where $z$ is the extraction axis), the undesired extraction of electrons from a negative ion source is reduced and it is due to collisions. The electron transport is studied with a kinetic model, including Vlasov–Poisson effects and atomic collisions. The integrodifferential equations (IDE) resulting from a reduction to a one-dimensional problem (1-D) by integration on characteristic orbits are strongly affected by the trapped orbits, as here evaluated; a kernel calculation with a partial wave approximation is introduced. Dependencies from the local drift velocity 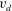$v_{d}$ and effective Larmor radius 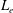$L_{e}$ are found. Solutions are investigated in simple cases with a constant electron current (no additional electron production). Equilibrium solution and electron conductivity are analytically obtained. Presheath solutions are discussed; the approximated conversion to differential equations that are adequate for presheath only (with moderated electric field gradient 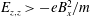$E_{z,z}>-eB_{x}^{2}/m$) and their numeric solutions coupled to Poisson equation are reported, and compared to iterative IDE solutions. Examples with different values of 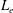$L_{e}$ and mean free path (mfp) ratio are described.

Type
Research Article
Information
Journal of Plasma Physics , Volume 81 , Issue 6 , December 2015 , 495810603
Copyright
© Cambridge University Press 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benilov, M. S. 2009 The Child–Langmuir law and analytical theory of collisionless to collision dominated sheaths. Plasma Sources Sci. Technol. 18, 014005.CrossRefGoogle Scholar
Brown, I. G. 2004 The Physics and Technology of Ion Sources, 2nd edn. John Wiley & Sons.Google Scholar
Caruso, A. & Cavaliere, A. 1962 The structure of the collisionless plasma-sheath transition. Nuovo Cimento 26, 1389–1404.Google Scholar
Cavenago, M. 2008 Negative ion transport inside collisional presheaths. Rev. Sci. Instrum. 79, 02B709.Google Scholar
Cavenago, M. 2010 Simulations of negative ion plasma sheaths. Rev. Sci. Instrum. 81, 02B501.Google Scholar
Chodura, R. 1982 Plasma–wall transition in an oblique magnetic field. Phys. Fluids 25, 1628–1633.Google Scholar
Daniłko, D. & Barral, S. 2015 Contribution of phase-energy correlation to classical mobility across a strong magnetic field. Phys. Scr. 90, 055601.Google Scholar
Dikman, S. M. & Meierovich, B. E. 1973 Theory of the anomalous skin effect in a plasma with a diffuse boundary. Sov. Phys. JETP 37, 835–843.Google Scholar
Emmert, G. A., Wieland, R. M., Menzel, A. T. & Davidson, J. N. 1980 Electric sheath and presheath in a collisionless, finite ion temperature plasma. Phys. Fluids 23, 809–812.Google Scholar
Forrester, A. T. 1996 Large Ion Beams. Wiley.Google Scholar
Franklin, R. N. 2003 The plasmasheath boundary region. J. Phys. D 36, R309–R320.Google Scholar
Hutchinson, I. H. 1987 A fluid theory of ion collection by probes in strong magnetic fields with plasma flow. Phys. Fluids 30, 3777–3781.Google Scholar
Lieberman, M. A. & Lichtenberg, A. J. 1994 Principles of Plasma Discharges and Material Processing. Wiley, especially Table 3.1 at page 57 and eq. (5.4.4) at page 142.Google Scholar
Mochalskyy, S, Lifschitz, A. F. & Minea, T. 2010 3D modelling of negative ion extraction from a negative ion source. Nucl. Fusion 50, 105011.Google Scholar
Morse, P. M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw-Hill, especially chap. 8.Google Scholar
Riemann, K. U. 1991 The Bohm criterion and sheath formation. J. Phys. D 24, 493–518.Google Scholar
Schmitz, H., Riemann, K. U. & Daube, Th. 1996 Theory of the collisional presheath in a magnetic field parallel to the wall. Phys. Plasmas 3, 2486–2495.Google Scholar
Self, S. A. 1963 Exact solution of the collisionless plasma–sheath equation. Phys. Fluids 6, 1762–1768.Google Scholar
Taccogna, F., Schneider, R., Longo, S. & Capitelli, M. 2008 Modeling of surface-dominated plasmas: from electric thruster to negative ion source. Rev. Sci. Instrum. 79, 02B903.Google Scholar
Taccogna, F., Minelli, P. & Longo, S. 2013 Three-dimensional structure of the extraction region of a hybrid negative ion source. Plasma Sources Sci. Technol. 22, 045019.Google Scholar
Takado, N., Miyamoto, K. & Hatayama, A. 2004 Numerical modeling of excited hydrogen atoms and their transport in hydrogen negative ion sources. Rev. Sci. Instrum. 75, 1777–1779.Google Scholar
Tonks, L. & Langmuir, I. 1929 General theory of the plasma of an arc. Phys. Rev. 34, 876–922.Google Scholar
Tsuda, T., Fukao, S. & Maeda, K. 1969 Gyromagnetic effect on the mobility of charged particles in weakly ionized gases. J. Appl. Phys. 40, 5280–5289.Google Scholar
Wolfram Mathematica®, www.wolfram.com; see also S. Wolfram 2003 The Mathematica Book, 5th edn., Champaign: Wolfram Media, especially for Series and NDSolve descriptions.Google Scholar