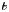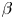Influence of magnetic configuration properties on kinetic ballooning modes in W7-X

Abstract

The stability properties of kinetic ballooning modes are investigated for a number of magnetic configurations of the stellarator Wendelstein 7-X. In particular, we consider the effects of the vacuum rotational transform, ${\raise.1pt-\kern-6pt\iota}$, and the mirror ratio. The analysis sheds light on the interplay between global magnetohydrodynamic configuration properties and local gyrokinetic stability, and is instrumental in the design of high-$\beta$ (the ratio of kinetic to magnetic pressure) operation scenarios. In particular, it is demonstrated that some Wendelstein 7-X magnetic configurations have a relatively low kinetic ballooning mode threshold.

1. Introduction

The physics of kinetic ballooning modes (KBMs) (Antonsen & Lane 1980; Tang, Connor & Hastie 1980), while being an extensively studied topic in tokamaks (Connor, Hastie & Taylor 1978; Antonsen & Lane 1980; Tang et al. 1980; Kotschenreuther 1986; Pueschel, Kammerer & Jenko 2008; Groebner et al. 2010, 2013; Snyder et al. 2011; Diallo et al. 2014), still remains relatively unexplored in stellarator geometry. Kinetic ballooning modes have been studied in helical devices, both linearly and nonlinearly (Ishizawa et al. 2013, 2015, 2019), and for the Helically Symmetric eXperiment (McKinney et al. 2019, 2021). Linear studies of KBMs in the optimized stellarator Wendelstein 7-X (W7-X) can be found in Aleynikova et al. (2018). However, for W7-X, there are a number of unanswered questions that need to be addressed.

The basic theory of KBMs was developed in Tang et al. (1980) and Hastie & Hesketh (1981). Here, the authors solve the gyrokinetic equation by expanding in ${\varepsilon =v^2_{{\rm thi}}/\omega ^2l^2_c\ll 1}$, where $v_{{\rm thi}} = \sqrt {2T_i/m_i}$ is the ion thermal speed, $l_c$ is the connection length and $\omega \ll v_{{\rm the}}/l_c$ is the mode frequency, with $v_{{\rm the}}$ the electron thermal speed. The general KBM equation retains magnetic drift resonances, gyro-averaging and magnetic compressibility effects. However, it was recently proved (Aleynikova & Zocco 2017) that an appropriate ${\beta }$-ordering (where $\beta$ is the ratio of thermal to magnetic plasma pressure) makes it possible to greatly simplify the general KBM equation, which turns out to be a simple diamagnetic modification to the ideal magnetohydrodynamic (MHD) ballooning equation, in many regimes of interest. In this analysis, it is fundamental to keep the magnetic drifts consistent with the equilibrium constraint $\boldsymbol {j}\times \boldsymbol {B}=\boldsymbol {\nabla }{p}$.

Typically, in W7-X geometry, the most unstable mode is persistently observed at very long wavelengths for a wide range of simulation parameters (Aleynikova et al. 2018). This is in contrast to tokamaks, where the most unstable mode can have a finite wavelength of the order of the inverse ion Larmor radius, $\rho _i$. This peculiar feature of KBMs in W7-X can pose a limit on the use of flux tubes for nonlinear numerical simulations.

There are only few nonlinear KBM numerical results that can be found in the literature. For example, in the work of McKinney et al. (2021), it was demonstrated that KBM transport becomes significant, potentially reaching a level of particle and heat fluxes comparable to those found in the electrostatic case, even for $\beta$ smaller than the critical $\beta$ for ideal ballooning mode destabilization. In some circumstances, the nonlinear transport due to KBMs is the dominant one, even if KBM growth rates (around $k_y\rho _i \approx 0.1$) are smaller than that of the ion temperature gradient (ITG)-driven instability (at larger $k_y\rho _i$). Taking into account an assumption that transport should (quasilinearly) scale like $\gamma /k_y^2$, this is expected. However, it is challenging to compare directly the quasilinear transport characteristics of ITG and KBM, since ITGs are mostly electrostatic, whereas KBMs are electromagnetic.

In W7-X, high-$\beta$ operation is one of the primary goals, since its best optimized configurations were conceived in that limit. However, in the design of W7-X, non-ideal instabilities were not considered. We now know that non-ideal effects do manifest themselves (Zocco, Mishchenko & Könies 2019; Strumberger & Günter 2020; Yu et al. 2020; Zocco et al. 2021; Aleynikova et al. 2021), and it seems reasonable to imagine that W7-X, for large enough $\beta,$ will be potentially unstable to non-ideal KBMs. In the present work, we provide an extensive study of KBM stability for a number of W7-X-relevant configurations. We emphasize the importance of keeping fully self-consistent plasma profiles, magnetic configuration parameters and local gyrokinetic parameters. This allows us to assess the stability properties of W7-X configurations, bridging the global properties of each configuration with the local stability studies.

This work is structured in the following way. In § 2 we present our simulation approach and discuss in great detail the self-consistent approach of the calculations which we propose for studies of electromagnetic instabilities. In § 3 we present results of linear electromagnetic Gyrokinetic Electromagnetic Numerical Experiment (GENE) (Jenko et al. 2000; Dannert & Jenko 2005) calculations for several W7-X configurations with different properties: first varying the rotational transform, ${\raise.1pt-\kern-6pt\iota}$, on axis and then varying the variation of the magnetic field strength, $B$, along the magnetic axis, the so-called mirror ratio. Based on these results we identify particular trends which lead to the most stable and unstable configurations. Conclusions are discussed in § 4.

2. Simulation details and different W7-X magnetic geometries

Gyrokinetic equations can be found in Jenko et al. (2000) and Goerler et al. (2011). The GENE code is used for our numerical study. The simulations are carried out for a range of gradients of density ($a/L_{{\rm ni},e}$) and temperature ($a/L_{{\rm Ti},e}$). Here $a$, $L_{{\rm ni},e}$ and $L_{{\rm Ti},e}$ are normalization lengths (in the present study, $a$ is an average minor radius), $a/L_{n} = -(a/n)\,{\rm d}n/{\rm d}r$ and $a/L_{T} = -(a/T)\,{\rm d}T/{\rm d}r$.

The equilibrium magnetic field is evaluated with the Variational Moments Equilibrium Code (VMEC) (Hirshman & Merkel 1986).

We consider a hydrogen plasma in the collisionless regime. Both ions and electrons are treated kinetically. For the particular frequency regime and $\beta$ considered in the study, trapped particle effects are not important. Here, ${\beta _{{\rm GENE}}} = {\beta _{i,e}} = \beta _{{\rm total}}/2 = (8{{\rm \pi} }{n_{i0}}{T_{{\rm ref}}})/(B^2_{{\rm ref}}),$ where ${T_{{\rm ref}}}$ is a reference temperature, ${B_{{\rm ref}}}$ a reference magnetic field and ${n_{i_0}}$ is the equilibrium ion density. Furthermore $T_i / T_e = 1$, $m_i / m_e = 1836$ and $a / R \approx 0.095$. Here, $T_{i}$ and $T_{e}$ are the ion and electron temperature, respectively, $R$ is the major radius and $a$ is the minor radius. Local calculations are performed for $r_{\mathrm {eff}}/a = 0.6$, unless specified otherwise and $r_{\mathrm {eff}}$ is the minor radius of the flux surface considered. This particular region in plasma is chosen because KBMs are expected to be present and experimentally detectable around this radial location (see results at the end of § 3).

For the investigation we select a flux tube with its centre at the outboard midplane of the so-called bean-shaped cross-section (see e.g. Geiger et al. 2014); this is known to be the most unstable flux tube for KBMs (Aleynikova et al. 2018). The flux tube extends one poloidal turn around the torus, which is enough for the instabilities we study in the present work (see figure 1). Note that this is not always the case (McKinney et al. 2021; Faber et al. 2018), especially close to marginality, where eigenfunctions are more extended along the field line. For each calculation with a rather small $\beta$ we check that the obtained results are unaffected by the number of poloidal turns. In our simulations we consider $k_x\rho _s = 0$, where $k_x$ is the radial wavenumber, and parallel magnetic fluctuations $\delta {B_{\|}}$ are taken into account.

Figure 1. Growth rate of electromagnetic instabilities for a $k_y\rho _s$ range in the EIM configuration of W7-X. Here $a/L_{{\rm Ti}} = a/L_{{\rm Te}} = 4$ and $a/L_n = 4$, $\beta _i = \beta _e = 2.3\,\%$ for $N_{\rm pol} = 1$ (purple, $+$) and $N_{\rm pol} = 2$ (green, $\times$).

The role of $\delta B_{\|}$ in microinstabilities is rather complicated and should not be underestimated since, for example, their absence in the pressure balance can generate spurious modes in slab geometry (Rogers, Zhu & Francisquez 2018). In W7-X, $\delta B_{\|}$ is essential for the destabilization of KBMs (see figure 2: the blue curve (stars) shows the case with $\delta B_{\|}$ effects taken into account when the difference between curvature and $\boldsymbol {\nabla } B$ drifts is retained; the green curve (crosses) is obtained without $\delta B_{\|}$ effects). The importance of $\delta B_{\|}$ effects was already demonstrated in Aleynikova et al. (2018) for a generic tokamak case. For ITG instabilities in toroidal geometry, $\delta B_{\|}$ provides a non-trivial cancellation of the magnetic drift modification due to equilibrium pressure gradients (Zocco, Helander & Connor 2015). The same was found for KBMs far from marginality (Aleynikova & Zocco 2017). Therefore, in our simulations, we always retain $\delta B_{\|}$ and we always retain the difference between curvature and $\boldsymbol {\nabla } B$ drifts, ${\omega _B} = {(\boldsymbol {k_\perp }\rho _s/2)\boldsymbol {\cdot }{v_{{\rm ths}}}\hat {\boldsymbol {b}}\times \boldsymbol {\nabla }{B}/B}, {\omega _\kappa = {(\boldsymbol {k_\perp }\rho _s/2)\boldsymbol {\cdot }{v_{{\rm ths}}}\hat {\boldsymbol {b}}\times (\hat {\boldsymbol {b}}\boldsymbol {\cdot }{\boldsymbol {\boldsymbol {\nabla }}}\hat {\boldsymbol {b}})}}$, where ${\omega _B}$ is the frequency associated with the $\boldsymbol {\nabla } B$ drift velocity and $\omega _\kappa$ is associated with the curvature one. Note that the common approximation ${\omega _B} = \omega _\kappa$ cannot be used. Figure 2, purple curve (pluses), shows the case without $\delta B_{\|}$ and ${\omega _B} = \omega _\kappa$. In Aleynikova & Zocco (2017) it was analytically shown that for a strongly unstable KBM ${\omega _B} = \omega _\kappa$ and neglecting $\delta B_{\|}$ indeed is enough to obtain the same eigenvalue equation as in the case where both terms are treated correctly. However, in figure 2 we see a noticeable difference, even though the KBM has a rather high growth rate. Approaching marginality without the exact approach would lead to a completely different linear threshold. We want to stress that the ITG instability, present at somewhat shorter wavelengths, is also affected by finite magnetic compressibility (Zocco et al. 2015).

Figure 2. Influence of $\delta B_{\|}$. Spectra for W7-X from GENE simulations. Here $a/L_{{\rm Ti}} = a/L_{{\rm Te}} = a/L_n = 4$, $\beta _i = \beta _e = 2.3\,\%$.

Electromagnetic effects should thus always be taken to be consistent with equilibrium pressure gradients. In the next subsections we discuss how one should obtain such a consistency.

2.1. Pressure profiles

In order to evaluate the stability of the plasma with the GENE code, it is necessary first to calculate the equilibrium using the VMEC. This code requires for a free-boundary calculation the following main physics input parameters: coil currents, an initial shape of the plasma boundary together with the toroidal flux enclosed by this boundary and profiles of the plasma pressure and of either the toroidal current or the rotational transform, ${\raise.1pt-\kern-6pt\iota}$. In our calculations, the toroidal current profile is set to zero, i.e. we assume a net-current-density-free stellarator operation. In this study we evaluate the stability for the sets of configurations in which the coil currents are fixed, while the pressure profile and plasma boundary change. This procedure roughly approximates the evolution of a heated plasma within a discharge with negligible bootstrap currents and no current drive. For simplicity, we parametrize the plasma pressure profile with

(2.1)\begin{equation} \beta = \beta_0(1-x^p)^q, \end{equation}

where $\beta _0$, $p$ and $q$ are free parameters and $x = (r_{\mathrm {eff}}/a)^2$ is the VMEC radial coordinate. Therefore, the pressure gradient and volume-averaged $\langle \beta \rangle$ are

(2.2)\begin{gather} \beta' = \beta_0 q p x^{p-1}(1-x^p)^{q-1}, \end{gather}

(2.3)\begin{gather} \left\langle \beta \right\rangle = \frac{\int{\beta \,{\rm d}V}}{\int{\,{\rm d}V}} \approx \frac{\int{\beta x\,{\rm d}x}}{\int{x\,{\rm d}x}}. \end{gather}

Here prime denotes the derivative with respect to $x$.

The actual model of pressure profile has been chosen by inspecting the experimentally observed ones. Particular care is taken in choosing the free parameters when generating profiles with desired values $\beta (x_1)$ at the local position, $x_1$, of the flux tube simulation, its local gradient and the volume-averaged $\langle \beta \rangle$. Continuous variation of any of these three quantities results in a continuous variation of the plasma pressure profile. The same parametrization is used in the ray-tracing code TRAVIS (Marushchenko, Turkin & Maassberg 2014) to model, for example, electron cyclotron current drive and electron cyclotron emission in W7-X.

The GENE code uses different input parameters, i.e. the normalized density and temperature gradients. Assuming that $n_e = n_i = n$ and $\sqrt {\langle B^2\rangle '} / \sqrt {\langle B^2\rangle } \ll (nT_i + nT_e)' / (nT_i + nT_e)$ leads to a relation for the inverse $\beta$ gradient scale length:

(2.4)\begin{equation} \frac{\beta'}{\beta} = \frac{(nT_i + nT_e)'}{nT_i + nT_e} = \frac{n'}{n} + \frac{T'_i + T'_e}{T_i+ T_e}. \end{equation}

Note that $\sqrt {\langle B^2\rangle }$ here and below is the flux surface-averaged value.

Figures 3 show different sequences of profiles with different correlations of the $\beta$ parameters. First, figure 3 demonstrates profiles which have the local $\beta$ equal to the volume-averaged $\beta$ and fix the inverse gradient scale to a fixed value. Further in this paper we are using this type of the profiles. Figure 4 shows profiles which fix the $\beta$ gradient and the local $\beta$ value at the chosen location at the expense of different volume-averaged $\beta$ values. Finally, figure 5 fixes the local and the volume-averaged $\beta$ values and varies the gradient of $\beta$ at the position of interest.

Figure 3. Profiles of $\beta$ with ${\beta '}/{\beta } = {n'_i}/{n_i} + {T'_i}/{T_i} = {n'_e}/{n_e} + {T'_e}/{T_e} = 8$ for different local $\beta$ values at $s =(r_{\mathrm {eff}}/a)^2 = 0.36$ (marked with a vertical dashed line), $\beta _{{\rm loc}} = \langle \beta \rangle$. Note that local $\beta$ here is $\beta _{{\rm loc}} = \beta _i + \beta _e$.

Figure 4. Profiles of $\beta$ with ${\beta '}/{\beta } = {n'_i}/{n_i} + {T'_i}/{T_i} = {n'_e}/{n_e} + {T'_e}/{T_e} = 8$ for fixed $\beta _{{\rm loc}} = 4\,\%$ at $s =(r_{\mathrm {eff}}/a)^2 = 0.36$ (marked with a vertical dashed line) and different $\langle \beta \rangle$. Note that local $\beta$ here is $\beta _{{\rm loc}} = \beta _i + \beta _e$.

Figure 5. Profiles of $\beta$ for fixed local $\beta = 3\,\%$ at $s =(r_{\mathrm {eff}}/a)^2 = 0.36$ (marked with a vertical dashed line) and fixed $\langle \beta \rangle = 3\,\%$ with different ${\beta '}/{\beta } = {n'_i}/{n_i} + {T'_i}/{T_i} = {n'_e}/{n_e} + {T'_e}/{T_e}$.

2.2. Magnetic configurations

In W7-X, magnetic configurations are conveniently labelled with a three-letter code. The first letter denotes the toroidal field variation along the magnetic axis, the so-called mirror ratio, ${\rm m.r.} = (B_{{\rm ax}}(\phi =0^\circ )-B_{{\rm ax}}(\phi =36^\circ ))/(B_{{\rm ax}}(\phi =0^\circ )+B_{{\rm ax}}(\phi =36^\circ )$), in steps of $1\,\%$ covering an interval of $1\,\%$. Letter ‘A’ starts with $0\,\%$, i.e. covers the interval $-0.5\,\%$ to $0.5\,\%$, letter ‘B’ thus means ${\rm m.r.}=1\,\%$ with the respective interval and so on up to ${\rm m.r.}=15\,\%$ (‘P’) when larger steps are used to cover a larger range of ${\rm m.r.}$ (Geiger, Maassberg & Beidler 2008). The second letter encodes the value of ${\raise.1pt-\kern-6pt\iota}$ on axis such that the letter ‘B’ is used for the so-called low-${\raise.1pt-\kern-6pt\iota}$ configurations with ${\raise.1pt-\kern-6pt\iota} =5/6$ at the boundary, letters ‘I’ or ‘J’ are characteristic for standard-configuration-like magnetic field with the 5/5-islands at the boundary and letters in the range of ‘T’ point to high-${\raise.1pt-\kern-6pt\iota}$ configurations with the 5/4-islands forming the boundary. The specific letter depends on the global shear in the configurations. The third letter is an indicator of the horizontal plasma position in such a way that the letter ‘M’ denotes no horizontal shift and ‘lower’ letters (towards ‘A’) are increasingly outward-shifted while ‘higher’ letters (towards ‘W’) are increasingly inward-shifted.

In this study we consider several configurations, all without a horizontal shift: EBM, ETM, EIM, AIM and KIM. The EIM configuration, often referred to as ‘standard configuration’, is MHD-stable up to a volume-averaged $\beta$ (${\approx }5\,\%$). Configurations EBM and ETM are taken as counterparts of the EIM configuration with respect to ${\raise.1pt-\kern-6pt\iota}$, since they have the same mirror ratio and no shift but different ${\raise.1pt-\kern-6pt\iota}$ on axis, low and high, respectively. Configurations AIM and KIM can be seen as counterparts of the EIM configuration with respect to the mirror ratio, since they have the same ${\raise.1pt-\kern-6pt\iota}$ on axis and no shift but different mirror ratio, low (zero) and high, respectively. Such a set of W7-X magnetic configurations allows one to analyse the influence of mirror ratio and ${\raise.1pt-\kern-6pt\iota}$ on KBM destabilization separately from other configuration properties.

Note that all W7-X vacuum configurations have a different maximum of $|\boldsymbol {B}|$ and $\sqrt {\langle B^2\rangle }$ on the flux surface (see figure 6). To obtain the same local $\beta$ at a prescribed position $s$ with the same pressure profile, the magnetic fields in these configurations have to be normalized (by varying coil currents) to obtain the same $\sqrt {\langle B^2\rangle }$ on the flux surface (see figure 7). The normalization factors ($2.5/\sqrt {\langle B^2(0)\rangle }$) for each configuration are: ETM, 1.048; EBM, 1.0; EIM, 0.898; AIM, 1.0; KIM, 1.089.

Figure 6. Maximum of $|\boldsymbol {B}|$ (dashed curves) and $\sqrt {\langle B^2\rangle }$ (solid) on the flux surface, $s=({r_{\mathrm {eff}}}/{a})^2$, for different vacuum magnetic configurations of W7-X. Note that the central value of the maximum of $|\boldsymbol {B}|$ only coincides with the average $B$ value for the configuration AIM with a vanishing mirror field, while for the others there is a deviation according to the mirror field present in the particular configuration.

Figure 7. Maximum of $|\boldsymbol {B}|$ (dashed curves) and $\sqrt {\langle B^2\rangle }$ (solid) on the flux surface, $s=({r_{\mathrm {eff}}}/{a})^2$, for different normalized vacuum magnetic configurations of W7-X.

Once we construct a finite $\beta$ equilibrium, we see the $\beta$ effect on the equilibrium (diamagnetic effect and Shafranov shift) which is shown in figure 8. We note that although the deviation from the vacuum field is noticeable, the assumption $((\sqrt {\langle B^2\rangle '}/{\sqrt {\langle B^2\rangle }}) \approx 0.2) \ll ({(nT_i + nT_e)'}/({nT_i + nT_e}) = 4)$ still holds.

Figure 8. Maximum of $|\boldsymbol {B}|$ (dashed curves) and $\sqrt {\langle B^2\rangle }$ (solid) on the flux surface, $s=({r_{\mathrm {eff}}}/{a})^2$, for normalized EIM configuration. Blue, vacuum case; orange, $\langle \beta \rangle =4.9\,\%$.

3. Dependence of the KBM instability threshold on magnetic configuration

In previous simulations, it has typically been seen that the KBM instability threshold lies below that of ideal MHD ballooning modes. W7-X has been optimized to be MHD-stable up to very high $\beta$ values in most of the region of configuration space of the coil system. In Aleynikova et al. (2018) the expectation that the KBM instability threshold should be related to the ideal MHD one was confirmed in W7-X geometry. However, different magnetic configurations of W7-X may manifest different behaviour with respect to the KBM destabilization. Thus, it is important to systematically study the dependence of the KBM instability threshold on the magnetic configuration in order to complement our present knowledge on KBM destabilization in W7-X, and to be able to control KBMs in future experiments.

The results of GENE simulations for three W7-X configurations with different mirror ratios are shown in figure 9. For these calculations, we used the same density and temperature gradients, $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$, and $k_y\rho _s$ was kept equal to $0.05$ to capture only the most unstable KBMs. Calculations performed for neighbouring $k_y\rho _s$ (as low as $0.03$ and as high as $0.1$) demonstrate the same trends. To fix the ratio between the two gradient scale lengths such that $(a/L_{{\rm Ti},e})/(a/L_{{\rm ni},e}) = 1$ results in a significant stabilization of ITG and TEM (Alcusón et al. 2020). This is an ideal condition for a KBM study: even for small $\beta$ values or gradients the KBM is not completely hidden under the other instabilities. The growth rates in figure 9 are displayed as a function of $\beta$. Approximate critical $\beta$ values (for AIM, EIM and KIM configurations) corresponding to the point of marginal KBM stability are shown. We stress that we do not perform an extrapolation of the growth rates to marginal values; all data points on the presented plots are GENE simulations (and the growth rates are not zero there, they have a small but finite value).

Figure 9. Dependence of KBM growth rate on $\beta$ with $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$ and $k_y\rho _s = 0.05$, in three different W7-X configurations with different mirror ratio: AIM, EIM and KIM.

Two of these configurations, AIM (purple, pluses) and KIM (blue, stars), have low and high mirror ratios, respectively, whereas the other configuration, EIM (green, crosses), also known as the standard configuration, is MHD-stable up to $\langle \beta \rangle =5\,\%$, where $\langle \beta \rangle$ is a plasma volume-average $\beta$, not to be confused with a local one. All these configurations are characterized by a standard rotational transform on axis, ${\raise.1pt-\kern-6pt\iota} (0) \approx 0.85$, and have no radial shift. The AIM configuration has a zero mirror ratio, while the EIM configuration has an intermediate mirror ratio = $4\,\%,$ whereas the KIM configuration corresponds to a case with a higher mirror ratio = $10\,\%$.

The intersection of the growth rate curve of the KBM branch with the horizontal axis in figure 9 suggests that the critical $\beta _{{\rm ref}}$ of KBM destabilization in the configuration with zero mirror ratio (AIM) is $\beta _{{\rm crit}} \approx 0.82\,\%$ while, for the configurations with the higher mirror ratio (EIM and KIM), it is $\beta _{{\rm crit}} \approx 0.98\,\%$ and $\beta _{{\rm crit}} \approx 1.05\,\%$, respectively. Thus, we conclude that the magnetic configurations with higher mirror ratio have a higher threshold for KBMs.

Simulation results for the other set of W7-X configurations with different ${\raise.1pt-\kern-6pt\iota} (0)$ are shown in figure 10. Two of these configurations, EBM (purple, pluses) and ETM (blue, stars), presented here are low- and high-${\raise.1pt-\kern-6pt\iota} (0)$ counterparts of the standard configuration EIM (green, crosses). All these configurations are characterized by a standard mirror ratio ($4\,\%$) and have no radial shift. The EBM configuration has ${\raise.1pt-\kern-6pt\iota} (0) \approx 0.74$, the EIM configuration is a standard one with ${\raise.1pt-\kern-6pt\iota} (0) \approx 0.85$ and the ETM configuration is a case with a high ${\raise.1pt-\kern-6pt\iota} (0) \approx 1.02$.

Figure 10. Dependence of KBM growth rate on $\beta$ with $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$ and $k_y\rho _s = 0.05$, in three different W7-X configurations with different value of ${\raise.1pt-\kern-6pt\iota}$ on axis: EBM, EIM and ETM.

For the EBM configuration, $\beta _{{\rm crit}} \approx 0.85\,\%$, the $\beta _{{\rm crit}}$ of the EIM configuration is $\approx 0.98\,\%$ and for the ETM configuration, $\beta _{{\rm crit}} \approx 1.02\,\%$. Thus, the critical $\beta$ values for KBM destabilization show a clear trend as ${\raise.1pt-\kern-6pt\iota} (0)$ is changed: configurations with a smaller ${\raise.1pt-\kern-6pt\iota} (0)$ show an earlier destabilization of KBMs than those with a higher ${\raise.1pt-\kern-6pt\iota} (0)$.

Note that this result confirms the expectation that KBM stability should be related to the value of ${\raise.1pt-\kern-6pt\iota}$. This can be demonstrated analytically using the simplified KBM equation (Aleynikova & Zocco 2017). Even in fully three-dimensional geometries, i.e. stellarator, a simplified KBM equation can be found (see Aleynikova et al. 2018, equation (2.5)) to give valuable insight. We consider the simple case in which the equilibrium magnetic field as well as the Jacobian are independent of the coordinate along $\boldsymbol {B}$ and $k^2_\perp = k^2_y$, $\boldsymbol {k}_{\perp }$ is the wavevector across the equilibrium magnetic field, magnetic shear ${\hat {s}} \approx 0$ and $y$ is a coordinate perpendicular to field line inside the flux surface. Then, Fourier transforming the cited simplified equation for the KBMs results in

(3.1)\begin{equation} \frac{b}{\beta_i{\sqrt{g_B}}^2}\frac{{k_z^2}{v_{{\rm thi}}^2}}{\omega^2} = \frac{{\omega_B} + {\omega_\kappa}}{\omega^2}{\omega_p} + \frac{k_y^2{\rho_i^2}}{2}\left[1 - \frac{\omega_{*i}}{\omega} \left(1 + {\eta_i}\right)\right] + \frac{\beta_i}{2} \frac{{\omega_p}^2}{{\omega}^2}, \end{equation}

where $\sqrt {g_B}$ is the determinant of the Jacobian matrix, $b=k_{\perp }^{2}v_{{\rm thi}}^{2}/2\varOmega _{i}^{2}B,$ $\varOmega _{i}(B)=m_{i}c/(eB)$ is the ion cyclotron frequency, ${\eta _i} = L_{n_i}/L_{T_i}$, $\omega _{*i,e} = \frac {1}{2} k_y{\rho _{i,e}}v_{{\rm th}}/L_n$ and ${\omega _p} = {\omega _{*i}}(1 + {\eta _i}) - {\omega _{*e}}(1 + {\eta _e})\equiv \omega _{pi}+\omega _{pe}$.

Let us set ${\omega } = {{\omega }_r} + i{\gamma }$, which allows us to find ${{\omega }_r} = \frac {1}{2}{\omega _{*i}}(1 + {\eta _i})$ (see details in Aleynikova & Zocco (2017)) and to derive an expression for a critical ${\beta }$ in this local limit of long wavelength:

(3.2)\begin{align} \beta_{{\rm crit}} & = \sqrt{\frac{\omega_B}{\omega_p}\left[\frac{\omega_B}{\omega_p} + b\frac{k^2_zv^2_{{\rm thi}}}{\omega_B\omega_p {\sqrt{g_B}}^2}\right]} - \frac{\omega_B}{\omega_p} \sim \frac{L_p}{R}\left\{\sqrt{1+ \frac{2k^2_zR^2}{\sqrt{g_B}^2}} - 1\right\} \notag\\ & \approx \frac{L_p}{R}\left\{\sqrt{1+ \frac{2\iota^2}{\sqrt{g_B}^2}} - 1\right\}. \end{align}

Thus the higher the ${\raise.1pt-\kern-6pt\iota}$ we have, the larger the KBM threshold we expect. Even though the assumptions made in deriving the equation are very limiting, a rough quantitative comparison can be made between (3.2) and the trend between $\beta _{{\rm crit}}$ and ${\raise.1pt-\kern-6pt\iota} (0)$ observed numerically (figure 10). Taking the difference between ${\raise.1pt-\kern-6pt\iota} (0)$ for those configurations to be roughly $0.1$, $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$ and assuming that $\sqrt {g_B}^2\approx 1$, we obtain a difference between $\beta _{{\rm crit}}$ of approximately 0.1 %. This seems to be a reasonable number.

We therefore conclude that, although W7-X has been optimized to be MHD-stable up to a very high $\beta$, some W7-X magnetic configurations have a relatively ‘early’ KBM threshold. This KBM threshold is sensitive to configuration parameters and, in principle, can be controlled to achieve a desired effect (stabilization or destabilization) on KBMs. Note that the pressure gradients used for the presented calculations are relatively high; nevertheless they are relevant for the high-performance W7-X experiments. The critical $\beta$ values found in the present work are therefore somewhat lower than for standard scenarios.

Relying on this knowledge, we propose two new theoretical configurations to highlight our findings. Combining lower-${\raise.1pt-\kern-6pt\iota}$ and a low mirror field, and combining high-${\raise.1pt-\kern-6pt\iota}$ with a high mirror field lead to two configurations, ABM and KTM, respectively, which extend the findings from figures 9 and 10 with respect to the lowest and the highest KBM thresholds. Configuration ABM: mirror ratio = ($0\,\%$), ${\raise.1pt-\kern-6pt\iota} (0) \approx 0.74$ and no shift. Configuration KTM: mirror ratio = ($10\,\%$), ${\raise.1pt-\kern-6pt\iota} (0) \approx 1.02$ and no shift. Simulation results for both of these configurations are presented in figure 11. For the ABM configuration, $\beta _{{\rm crit}} \approx 0.8\,\%$; for the KTM configuration, $\beta _{{\rm crit}} \approx 1.24\,\%$. Note that $\beta _{\text {crit ABM}} < \beta _{\text {crit AIM}} < \beta _{\text {crit EIM}} < \beta _{\text {crit KIM}} < \beta _{\text {crit KTM}}$ which is in agreement with the expected trends. Such a dependence of the KBM threshold on the ${\raise.1pt-\kern-6pt\iota}$ value can be explained by the effect of ${\raise.1pt-\kern-6pt\iota}$ on the field line bending term, see Eq. (3.2), which is stabilizing and increases with ${\raise.1pt-\kern-6pt\iota}$ itself. The dependence on the value of the mirror ratio seems to be more complicated. An inspection of Eq. (3.2) reveals that this effect is not accounted for explicitly, due to the simplifying assumptions. However, we do observe an impact of the mirror ratio on the eigenfunctions. These become less peaked and show finer structure when the mirror ratio is increased, thus potentially increasing the parallel wavenumber in the stabilizing term. This sensitivity to the mirror ratio might indicate that, close to marginality, KBMs feature mode structures similar to TEMs, that is: less ballooning, more extended, and with large variations along the field line. In general, these trends should hold for other magnetic geometries as well.

Figure 11. Dependence of KBM growth rate on $\beta$ with $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$ and $k_y\rho _s = 0.05$, in two different W7-X configurations: ABM (low mirror ratio and low ${\raise.1pt-\kern-6pt\iota}$ on axis) and KTM (high mirror ratio and high ${\raise.1pt-\kern-6pt\iota}$ on axis). Inconsistent calculations are shown in grey.

In order to show the importance of using consistent finite-$\beta$ equilibrium calculations we show the results obtained when using vacuum fields ($\beta _{{\rm equilibrium}}=0\,\%$) and adding $\beta$ only via the parameter choices in stability calculations. These are the grey curves in figure 11 showing them to deviate significantly from the consistently calculated results and therefore being unreliable.

The identified trends of high ${\raise.1pt-\kern-6pt\iota}$ on axis and high mirror ratio being beneficial for KBM stability are inferred from flux tube simulations, with the flux tube location unchanged. Yet, it is not possible to guarantee that these trends radially hold since they are identified with local simulation at the fixed radial position. Global simulations are free of such limitations and thus can complement our results. To overcome some limitations of the local approximation we scan through several radial positions (see figure 12), $s$, to confirm that the same trends previously discussed are observed for all $s$ which are favourable for KBMs. The calculations are performed in three different W7-X configurations (AIM: low mirror, standard ${\raise.1pt-\kern-6pt\iota} (0)$; EBM: standard mirror, low ${\raise.1pt-\kern-6pt\iota} (0)$; EIM: standard mirror, standard ${\raise.1pt-\kern-6pt\iota} (0)$) with different equilibrium $\langle \beta \rangle$ values: $\langle \beta \rangle = 2.0\,\%$, $\langle \beta \rangle = 2.5\,\%$ and $\langle \beta \rangle = 3.0\,\%$. As the trends hold for all radial positions, we conclude that, very likely, our findings will persist also globally. It is interesting to notice that with increasing $\langle \beta \rangle$ the position of the most unstable KBM is shifting towards the edge.

Figure 12. Radial KBM growth rate dependence, $k_y\rho _s = 0.05$ and $a/L_{{\rm Ti},e} = a/L_{{\rm ni},e} = 4$, in three different W7-X configurations: AIM, EIM and EBM. Left: $\langle \beta \rangle = 2.0\,\%$. Middle: $\langle \beta \rangle = 2.5\,\%$. Right: $\langle \beta \rangle = 3.0\,\%$.

4. Conclusion

Kinetic ballooning modes are undesirable for future fusion devices, due to their possible detrimental effect on confinement. In the present work we study several configuration properties which affect the KBM destabilization in W7-X.

Linear electromagnetic gyrokinetic numerical simulations of KBMs have been performed with the GENE code in finite-$\beta$ plasmas, for different magnetic configurations. The plasma equilibria used for these calculations were obtained using the VMEC keeping local gradients and global pressure profiles consistent.

Some properties of the magnetic configurations, such as the mirror ratio and the ${\raise.1pt-\kern-6pt\iota}$ profile, were studied independently in order to identify their influence on the stability of KBMs in W7-X. They appear to be more unstable in configurations with lower mirror ratio and lower ${\raise.1pt-\kern-6pt\iota} (0)$, which are also generally more unstable with respect to the ideal ballooning modes. The identification of these trends is instrumental for the planning of the upcoming W7-X campaign, OP2.

The identified trends were also verified and confirmed for several radial locations in the plasma, thus identifying regions where KBM activity is expected to be present and experimentally detectable.

Presented results already allow tackling experimentally relevant questions; however, it is still important to verify these findings nonlinearly to prove that the trends hold. That and a direct comparison of the KBM threshold with the associated ideal MHD stability threshold are a subject of future work. Although Aleynikova et al. (2018) suggest that low-$k_y$ KBMs are the counterparts of the ideal MHD modes and, therefore, their thresholds exhibit similar trends with varying configurations, a proper comparison of $\beta _{{\rm crit}}$ values for KBMs with the corresponding MHD modes for W7-X configurations still has to be performed. Another prominent configuration property affecting KBM stability is magnetic shear. A thorough study of the effect of magnetic shear on KBM stability in W7-X is ongoing (P. Mulholland, personal communication 2022).