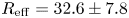Improved axial confinement in the open trap by the combination of helical and short mirrors

Abstract

The paper presents experimental results from the SMOLA device, which was built in the Budker Institute of Nuclear Physics for the verification of the helical mirror confinement idea. This concept involves active control of axial losses from the confinement zone in an open magnetic trap through the use of multiple mirrors that move in the plasma frame of reference. The discussed experiments focused on determining the cumulative effect of a helical mirror system in combination with a short segment of a stronger magnetic field. Combination of these two methods of axial flow suppression results in higher efficiency compared with each method individually. Different combinations of the mirrors were tested. The most effective flow suppression was observed if the short mirror was placed between the confinement region and the helical mirror. In this configuration, an effective mirror ratio of $R_{{\rm eff}} = 32.6\pm 7.8$ was achieved, along with a more than three-fold increase in plasma density within the confinement region. The possibility of a cumulative effect of different types of magnetic mirrors offers a way to improve the confinement performance of the reactor-grade mirror confinement devices.

1 Introduction

The potential of open magnetic systems to attain fusion-grade plasma has been reassessed over the past few decades (Bagryansky, Beklemishev & Postupaev 2019). Several projects using magnetic mirror devices for fusion with different methods of achieving good energy confinement, macroscopic and kinetic stability have been proposed (see, for example, Gota et al. 2019; Yakovlev et al. 2022; Jäderberg et al. 2023; Forest et al. 2024). Among them, the gas-dynamic multiple-mirror trap (GDMT) project was proposed in Budker INP (Skovorodin et al. 2023). This modular concept involves central gas-dynamic cell and separate modules for improved axial confinement. In general, multiple-mirror sections reduce the axial velocity of the plasma outflow through interactions of the ions with the periodic (corrugated) magnetic field (Burdakov & Postupaev 2018).

One of the possible improvements of the multiple-mirror technique involves moving maxima of the magnetic field along the axis to slow down the plasma outflow (Budker, Mirnov & Ryutov 1982; Beery, Gertsman & Seeman 2018). The axial movement of the magnetic corrugation can be obtained with the stationary magnetic field with helical symmetry if the plasma rotates (Beklemishev 2013). Such a system resembles a straightened stellarator with one important difference. In the closed magnetic surfaces of a stellarator, the radial electric field is maintained by plasma self-organisation processes. In a helical mirror system, a required spatial profile of the radial electric field can be set by proper biasing of endplates and limiters. This allows direct control of the $E \times B$ plasma rotation. Within the rotating plasma's reference frame, the periodical variations of the magnetic field move in the direction defined by the directions of the rotation and the helicity. The locally trapped particles gain additional momentum in the same direction. The motion of the rotating plasma in a helical magnetic field was described theoretically in Beklemishev (2016) and Chernoshtanov & Ayupov (2021). In terms of macroscopic parameters, the axial component of pressure gradient becomes steeper in presence of the axial Ampere's force. This force is created by the radial ion current and azimuthal component of the magnetic field. The potential energy of the ions in the external or ambipolar electric field is the energy source that drives the plasma motion. Therefore, Beklemishev (2016) predicted radial plasma expansion if the plasma axis is charged positively (including the case of the rotation in ambipolar electric field) and radial plasma contraction if the plasma axis is charged negatively. The latter case dramatically differs the linear helical system from the stellarator. In the case of a helical mirror, a proper configuration choice delivers both the confinement improvement and plasma pinching to the axis due to neoclassical effects (Beklemishev 2016).

Plasma flows in the helical magnetic field are investigated in a small-scale SMOLA helical mirror device (Postupaev et al. 2016; Sudnikov et al. 2017). The suppression of the axial plasma flow by the helical section was demonstrated earlier (Sudnikov et al. 2019). An improvement in the confinement was observed with an increase in the magnetic field, the corrugation ratio and the plasma rotation velocity (Sudnikov et al. 2020). The increase in plasma density in the entrance trap by the factor of 1.6 in helical configuration was achieved (Sudnikov et al. 2022a). The effect strongly depends on the direction of the plasma rotation (Sudnikov et al. 2022b).

One of the many issues of an embedding of the helical mirror system to a fusion grade is how effectively it can be combined with the strong (up to 20 T) short mirrors of the gas-dynamic central cell. This paper presents the latest experimental results on the axial plasma flows in the helical mirror system combined with the short segment of the stronger magnetic field. Combination of these two methods of axial flow suppression results in higher efficiency compared with each method individually.

2 Experimental set-up and parameters

The layout of the SMOLA helical mirror is presented in figure 1. The device was built for studies of a low-temperature hydrogen plasma flow through a 2.5-m-long transport section with helically symmetric magnetic field. Plasma was generated in a source with a magnetically insulated heated LaB$_6$ cathode (Ivanov et al. 2021). The plasma was then injected into a compact mirror trap in the entrance tank. In the following, we call this the confinement region. Plasma flows in the axial direction from the confinement region to the transport section. This section has two independent sets of magnetic coils, a solenoid for a straight field and a bispiral helical winding that forms a helical magnetic mirror. The spiral has $N = 12$ corrugation periods. We denote the field line without the periodic variation of the magnetic field module as the magnetic axis of the transport section. This axis has spiral shape, its radius depends on the helical to axial components of the magnetic field ratio. The last part of the device is the exit expander that contains an exit limiter and a radially segmented plasma receiver endplates. The axially symmetric confinement region, helically symmetric transport section and axially symmetric exit expander are matched together by the special correction units. The centre of the cathode is projected by the magnetic field line to the magnetic axis of the transport section and to the centre of the endplates. The vacuum tanks of the confinement region and the exit expander have the same volume and are pumped by identical turbomolecular pumps. The vacuum conductivity of the transport section is an order of magnitude lower than the pumping speed. A detailed description of the device can be found in Sudnikov et al. (2017).

Figure 1. Layout of the SMOLA helical mirror. Positions of the diagnostics used in this paper are indicated. Probe: a combined probe that includes a double probe and two emissive probes. D.Sp: Doppler spectroscopy. Mach: a combined probe that includes a planar Mach probe and two emissive probes. Here $z$ is the axial coordinate measured from the plasma source exit.

The experiments described in this paper were focused on the possible cumulative effects of a combination of a short classical magnetic mirror and the helical multiple-mirror section. In the following, we use the effective mirror ratio of the transport section $R_{{\rm eff}}$ as the figure of merit. The effective mirror ratio $R_{{\rm eff}}$ corresponds to the mirror ratio of the simple mirror, which provides the same suppression of the axial flow as the magnetic system under study. The definition of $R_{{\rm eff}}$ is introduced later in § 4.

In the worst case of no synergistic effect of the helical and the classical short magnetic mirrors, the effectiveness of the combined mirror system is equal to the effectiveness of its most effective part. This case presumably takes place, for example, in the combination of strong short mirror and weak axisymmetric multiple mirrors on its downstream side. In this example, all particles which have passed through the short mirror reside in the loss cone of the multiple-mirror section and do not interact with the magnetic field. In the best case, different techniques of axial flow suppression work independently of each other. Therefore, the effective mirror ratio can be in the range

(2.1)\begin{equation} \max[R_i]\leq R_{{\rm eff}}\leq\prod R_i, \end{equation}

where $R_i$ are the effective mirror ratios of the elementary parts of the mirror system.

The distribution of the guiding magnetic field at zero helical component is shown in figure 2. Plasma was trapped in the confinement region between the magnetic mirror in the plasma source (with a mirror ratio of $R_1=8$ in all experiments) and the transport section. The transport section had three different configurations of the guiding magnetic field. The first, which we refer to as the ‘basic configuration’, had a uniform magnetic field with a mirror ratio $R_2=3$. The other two configurations, which we call ‘mirror at the entrance’ and ‘mirror at the exit’, had local humps of the magnetic field with the mirror ratio of $R_2=6$ near the confinement region and near the expander, respectively. The configuration with humps on both sides may also be of interest, but it has not been tested due to power system limitations. The magnetic field of the transport section was either straight or helical. The mean corrugation ratio $R_{{\rm mean}}$, which is the ratio of the maximal and minimal magnetic field along the field line within the transport section averaged over the plasma cross-section, was $R_{{\rm mean}} = 1.52$ in the helical configuration (note that in a straight configuration $R_{{\rm mean}} = 1$ by definition).

Figure 2. Guiding magnetic field profiles. Red: ‘basic’ configuration. Green: ‘mirror at the entrance’. Blue: ‘mirror at the exit’.

The following diagnostics were actively used in the described experiments. Radially movable sets of electrostatic probes were installed in the confinement region ($z = 0.4$ m) and in four positions along the transport section at $z = 2.04$ m, $z = 2.4$ m, $z = 2.58$ m and $z = 3.48$ m (second, fourth, fifth and tenth corrugation period). Each set includes a double probe and two radially shifted emissive probes. Double probes at $z = 0.4, 2.04$ and 3.48 m measured $I$–$V$ characteristic, other probes were in ion saturation regime with electron temperature interpolated from other probes’ data. The emissive probes with thoriated tungsten wires were heated by the plasma during the initial part of the discharge and then provided simultaneous measurements of plasma potential and radial electric field. The reach of the probe working temperature was verified by thermal radiation of the wire. Diamagnetic loop was installed at $z = 0.6$ m to measure energy stored in the confinement region. Two imaging Doppler spectrometers ($z = 1.15$ and 5.3 m) were used to monitor plasma rotation (Inzhevatkina et al. 2021). The spectrometers also provide the ion temperature by measuring the Doppler broadening of the emission line of the charge-exchanged hydrogen.

The typical experimental waveforms are shown in figure 3. The time $t=0$ corresponds to the discharge initiation. The stationary plasma discharge builds up during the first 40–60 ms. Average values on the flattop of the discharge ($t=120$–180 ms) are used to plot radial profiles of the plasma parameters. The emissive probe reaches working temperature in $t\leq 40$ ms at radial coordinates $r\leq 6$ cm. At the outer region ($r=6$–8 cm), the heating takes up to $t=90$ ms. The temperature rise time is consistent with the estimations similar to Hershkowitz et al. (1983). At $t=185$ ms the plasma source is turned off to avoid damaging the probes.

Figure 3. Typical waveforms of plasma parameters in discharges with ‘basic’ straight ($R_{{\rm mean}} = 1$, red curves) and helically corrugated ($R_{{\rm mean}} = 1.52$) magnetic configurations: (a) the discharge current; (b) the voltage between the anode and the cathode of the plasma source; (c) the potential of the emissive probe at $z=0.4$ m; (d) the current of the double probe at $z=0.4$ m ($I$–$V$ curve measurement); (e) the current of the double probe at $z = 2.04$ m (the ion saturation current measurement); (f) the neutral hydrogen pressure at $z=0.4$ m; (g) the neutral hydrogen pressure at $z=4.34$ m.

The hydrogen flow rate from the gas feeding system into the plasma source was identical in all of the experimental discharges described in this paper. The plasma density between the mirrors in the confinement region depended on the effective mirror ratio of the transport section. The density was in the range $n = (1\unicode{x2013}4)\times 10^{18}\,{\rm m}^{-3}$, average ion temperature was $T_i \sim 5$ eV and electron temperature on the axis was $T_e \sim 20$ eV. The plasma rotation velocity in the discussed experiments was $\omega = (0.8\unicode{x2013}1.1)\times 10^6\,{\rm s}^{-1}$ in the entrance tank ($z = 1.15$ m) and $\omega = (0.5\unicode{x2013}0.7)\times 10^6\,{\rm s}^{-1}$ in the exit expander ($z = 4.34$ m). These values correspond to ion thermal velocity $V_{Ti} \sim 2.2\times 10^4\,{\rm m}\,{\rm s}^{-1}$, ion sound velocity $c_{s} \sim 4.4\times 10^4\,{\rm m}\,{\rm s}^{-1}$, axial velocity of the magnetic perturbations in the reference frame of rotating plasma $V_{z} = h\cdot \omega _{E\times B} / (2{\rm \pi} ) \sim (2.9\unicode{x2013}3.4)\times 10^4\,{\rm m}\,{\rm s}^{-1}$.

3 Experimental observation

The experimental signals were interpreted in the following way. We made about 20 identical experimental discharges in each magnetic configuration. Probe sets were moved radially between discharges. The data obtained by the diamagnetic loop and the spectrometers were averaged over the series of identical discharges. The averaged signals of the diamagnetic probes were numerically integrated over time.

Integrated signals of the diamagnetic loop stay constant at stationary phase of the discharge and decay in 0.05–0.2 ms after switching off the plasma source (figure 4). The decay process has two parts with different characteristic times. Here, we concentrate on the first stage of the decay. Both the stationary level and the decay time are affected directly by the magnetic configuration. The lowest values correspond to the ‘basic’ magnetic configuration, the highest values are observed in the helical configuration with the ‘mirror at the entrance’.

Figure 4. Diamagnetism of the plasma in the confinement region. Red: ‘basic’ straight magnetic configuration. Blue: ‘basic’ helical magnetic configuration.

Sample radial distributions of the plasma density measured by the double probes are shown in figures 5 and 6. The vertical error bars in these graphs correspond to the error of the $V$ curve fitting and the horizontal error bars correspond to the probe dimensions (the probe length is 6 mm for the unit installed at $z=0.40$ m, 4 mm for all other units).

Figure 5. Sample radial profiles of the plasma density in the confinement region: (a) straight magnetic configurations; (b) helical magnetic configurations and ‘basic’ straight magnetic configuration. Dots show experimental data, lines are fitting functions, green arrows show average values (calculation details are discussed in the text).

Figure 6. Sample radial profiles of the plasma density in the transport section. Magnetic configurations: (a) ‘basic’ straight; (b) ‘basic’ helical; (c) ‘mirror at the entrance’ straight; (d) ‘mirror at the entrance’ helical; (e) ‘mirror at the exit’ straight; (f) ‘mirror at the exit’ helical. Dots show experimental data, lines are fitting functions, different colours correspond to different axial coordinates of the probes.

One can note the significant difference in the radial profiles of the plasma density in both the confinement region and the transport section. The density in the confinement region increased with any improvement of the magnetic configuration. The most prominent difference is observed between the straight and helical configurations. The highest density corresponds to the helical configuration with the ‘mirror at the entrance’.

In general, we have three different parameters showing the confinement improvement: maximal density, stationary diamagnetism and decay time. All of them change similarly with the magnetic configuration.

We averaged the plasma density over the cross-section of the plasma column to obtain numerical measure of the density change at different axial coordinates. Later in the text we operate with the density averaged over the corresponding cross-section (see the green arrows in figure 5). For the purpose of the integration we assumed that radial distributions of plasma parameters are axially symmetric and that the vertical displacement of the plasma axis is negligible compared with the plasma radius for all operation regimes. The first assumption relies on the axially symmetric configuration of the plasma source and confinement region and on the bispiral configuration of the helical magnetic system which does not deform the plasma shape at small displacements of the plasma axis. The second is based on the second-order rotational symmetry of the helical magnetic system with respect to the axis of the diagnostic port. The horizontal position of the plasma axis was found for every magnetic configuration as the point of zero radial electric field.

The following analytical function was used to fit the experimental radial profiles:

(3.1)\begin{equation} f(r)=a_1 \exp \left(-\left(\frac{r-r_0}{r_1}\right)^4\right)+a_2 \exp\left(-\left(\frac{r-r_0}{r_2}\right)^2\right).\end{equation}

In this equation, $r$ is the radial coordinate relative to the geometric axis of the vacuum chamber, $r_0$ is the position of the centre of the plasma stream where the radial electric field changes sign, the fitting parameters $r_1$ and $r_2$ are characteristic radii of the plasma stream and the density flat-top and $a_1$ and $a_2$ are the corresponding amplitudes.

Average density dependence across the transport section is shown in figure 7. In most configurations, the density decreases along the transport section. According to the model of the radial and axial transport (Beklemishev 2016; Sudnikov et al. 2017), one can assume exponential dependence $n(r,z) = n(r,0) \exp (-z/z_0(r))$. We can use the same form as a rough estimate of average density dependence.

Figure 7. Average density in the transport section: (a) ‘basic’ magnetic configuration; (b) ‘mirror at the entrance’; (c) ‘mirror at the exit’.

The average values of density, diamagnetism and decay time describing the confinement between the mirrors and characteristic length of the density decrease in the transport section are summarised in table 1.

Table 1. Average density, diamagnetism and confinement time in different magnetic configurations.

The data presented can be interpreted in the following way. Local mirrors at the entrance or at the exit of the transport section reduce the axial particle flux compared with the ‘basic’ configuration; therefore, the number of particles in the confinement zone, diamagnetism (in one of the configurations) and decay time increase. In the straight ‘basic’ and ‘mirror at the entrance’ configurations, plasma flows through the transport section with axial velocity gradually increasing with distance, the Mach number is about $M\sim 0.5$–0.6 in the central part of the transport section and rises to $M\sim 1$ at the exit expander (Inzhevatkina et al. 2024). Density decreases accordingly. In contrast, the mirror at the exit reflects a certain amount of particles that reduces the axial flow velocity in the transport section ($M\sim 0.2$ in the discussed experiments) and makes the density along the transport section almost constant.

The helical magnetic field suppresses the outflow significantly in all magnetic configurations. This effect is stronger than the effect of simple mirrors and works in combination with them. Average velocity in the middle of the transport section is lower due to axial movement of the trapped particles ($M\sim 0.2$–0.3 across the cross-section; Inzhevatkina et al. 2024), local velocity on axis may change its direction. The density decreases exponentially, $n=n_0\exp (-z/z_0)$, with the characteristic length $z_0$ being less than the axial size of the transport section. Remarkably, the characteristic length is almost the same in ‘basic’ and ‘mirror at the entrance’ configurations, where there are no additional barriers. Slope in the ‘mirror at the exit’ configuration is less steep. Decreased losses result in higher density and diamagnetism and longer decay time.

4 Effective mirror ratio evaluation

The improved confinement presented previously can be described by the effective mirror ratio. The ion mean free path in the confinement region of the trap is less than the distance between mirrors, each mirror disturbs the ion distribution function only in its own vicinity. The losses through each mirror can be estimated as $F = n c_s S_m$ (Ryutov 1988), where $n$ and $c_s$ are the density and the sound velocity of ions in the entrance trap, $S_m$ is the cross-section of the plasma in the mirror. The losses are usually re-determined using the plasma cross-section in the minimal magnetic field $S_0 = S_m R$, where $R$ is the corresponding mirror ratio.

On the stationary phase of the discharge the losses are balanced with new ions from the plasma source and the return flux, which is generated by the transport section. The rate of plasma neutralisation and neutral gas pumping matches the rate of plasma source feeding in steady state. The particle balance inside the confinement region can be written in the following form:

(4.1)\begin{equation} n c_s S_0\left(\frac{1}{R_1}+\frac{1}{R_2}\right)=F_{{\rm feed}}+F_{{\rm return}}, \end{equation}

where $R_1 = 8$ and $R_2 = 3$ are the simple mirror ratios of the minimal magnetic field to the plasma source field and to the guide magnetic field of the transport section, $F_{{\rm feed}}$ is the flux from the plasma source and $F_{{\rm return}}$ is the return flux from the transport section. The difference of the outflow $n c_s S_0$ and return $F_{{\rm return}}$ fluxes at the inlet of the transport section can be used to define the effective mirror ratio of the transport section $R_{{\rm eff}}$:

(4.2)\begin{equation} F_{{\rm feed}}=\frac{n c_s S_0}{R_1}+\left(\frac{n c_s S_0}{R_2}-F_{{\rm return}}\right)=nc_s S_0 \left(\frac{1}{R_1}+\frac{1}{R_{{\rm eff}}}\right).\end{equation}

Taking into account that $F_{{\rm feed}}$ and $S_0$ are constant in all discussed experiments and $c_s$ changes insignificantly, one can equate the fluxes in two different magnetic configurations:

(4.3)\begin{equation} \frac{1}{R_{{\rm eff}}} = \frac{n_{{\rm ref}}}{n_{{\rm impr}}} \left(\frac{1}{R_1}+\frac{1}{R_2}\right) - \frac{1}{R_1}.\end{equation}

This equation can be used directly to estimate the effective mirror ratio from the average density measured by the probe. It also can be used for the stationary level of diamagnetism assuming that the ion and electron temperatures do not change significantly from one configuration to another. Experimental errors of directly measured density, diamagnetism and confinement time lead to wide and asymmetric confidence intervals of the effective mirror ratio when $R_{{\rm eff}}\gg R_1$.

On the decay phase, the flux from the plasma source turns to zero, and the number of particles in the confinement region can be described as

(4.4)\begin{equation} \frac{{\rm d} N}{{\rm d} t} ={-} n c_s S_0\left(\frac{1}{R_1}+\frac{1}{R_{{\rm eff}}}\right), \end{equation}

where $N \sim n S_0 L$ is the number of particles and $L$ is the length between mirrors. Density decays exponentially as $n = n_0 \exp (-t/\tau )$ with time constant

(4.5)\begin{equation} \frac{1}{\tau} = \frac{c_s}{L} \left(\frac{1}{R_1}+\frac{1}{R_{{\rm eff}}}\right). \end{equation}

Therefore, the effective mirror ratio can be also estimated as

(4.6)\begin{equation} \frac{1}{R_{{\rm eff}}} = \frac{\tau_{{\rm ref}}}{\tau_{{\rm impr}}} \left(\frac{1}{R_1}+\frac{1}{R_2}\right)-\frac{1}{R_1} .\end{equation}

The $R_{{\rm eff}}$ values can be calculated from the data in table 1. The resulting values are given in table 2. The last column gives the weighted average of three methods.

Table 2. Estimations of effective mirror ratio based on average density, diamagnetism and confinement time. The last column lists the effective mirror ratio averaged over three methods. Brackets show the limits of highly asymmetric confidence intervals.

The effective mirror ratio in the ‘basic’ configuration equals by definition to the simple mirror ratio of the transport section, $R_{{\rm eff}}=R_2$. The formally calculated confidence intervals show the minimal level of error of each method in the experiments discussed.

The straight configuration with the additional short mirror at the entrance is the useful benchmark for the effective mirror ratio. The particle losses in this configuration can also be estimated as gas-dynamic ones (Ryutov 1988), the length of the confinement region remains unchanged, therefore the effective mirror ratio is assumed to be equal to the mirror ratio of the simple mirror, $R_{{\rm eff}} = R_{{\rm entrance}} = 6$. According to this benchmark, a calculation based on the stationary diamagnetism tends to slightly underestimate the effective mirror ratio, whereas the calculation based on the decay time, the averaged density and the weighted value match the expected value within the confidence intervals.

The helical magnetic field provides a higher effective mirror ratio compared with any straight field even in the ‘basic’ configuration. Combination of the helical magnetic field with the short mirror improves the confinement. The highest effective mirror ratio ($R_{{\rm eff}}=32.6\pm 7.8$) corresponds to the configuration with the mirror at the entrance of the transport section.

5 Discussion and summary

The experiments discussed in this paper demonstrated that the optimistic side of (2.1) can be realised with the optimally combined magnetic system. The combination of a short magnetic mirror and a helical plug is more effective than either component alone. At the same time, the most effective combination might be counterintuitive. The highest magnetic field of the helical section is lower than the magnetic field of the short mirror. In a classical multiple-mirror system, the majority of particles that become trapped within periodic potential wells are likely to be reflected from the short mirror back into the transport section, thereby diminishing the overall efficiency of the system.

Let us consider the velocity space of the ions in the transport section near the short mirror (for example, at $z = 2$ m in figure 2). This velocity space is schematically shown in figure 8, it can be divided into three domains. The loss cone with the negative axial velocity (denoted as ‘A’ in figure 8) contains the particles which return back from the transport section and can pass through the short mirror into the confinement region. The loss cone with positive axial velocity (denoted as ‘C’) contains the particles that escaped from the confinement region. Part of the space outside of the loss cones (denoted as ‘B’) contains the particles reflected from the short mirror.

Figure 8. Schematic view of the velocity space in the helical configuration with the short mirror at the entrance. Solid lines show the borders of the loss cone of the short mirror, red sectors correspond to the particles trapped in the corrugations of the helical field. Here $R_s=2$ corresponds to the mirror ratio between the transport section and the short mirror. Zone labels are discussed in the text. Vertical dotted line show the axial velocity of the magnetic corrugations, horizontal dotted lines show the characteristic thermal velocity.

Particles trapped in the periodic magnetic field of the multiple-mirror system have an average axial velocity of the order of $V_z=h\omega _{E\times B}/2{\rm \pi}$ and a transverse velocity of the order of $V_{Ti}$. With the velocities and mirror ratio of the discussed experiments, these particles are mostly located in the loss cone A and can pass back into the confinement region.

This explanation results in the verifiable consequence. The described combination of simple and helical mirror will have cumulative effectiveness if the axial velocity of the magnetic corrugation is high enough to drag the particles into the loss cone of the strong mirror, i.e. $\tan ^{-1}(V_{Ti}/V_z)<\sin ^{-1}(1/\sqrt {R_s})$, where $R_s$ is the mirror ratio between the multiple-mirror section and the strong mirror. In the case of the SMOLA device, this threshold is $R_s\sim 3.5$. Experiments near this threshold require an upgrade of the magnetic system, which can be performed in the timeframe of 1–2 years.

The possibility of the cumulative effect of different types of the magnetic mirrors gives a way to improve the confinement efficiency of the GDMT project (Skovorodin et al. 2023). A magnetic configuration with the ‘mirror at the entrance’ gives better results in a small-scale device, but it may be more challenging to push particles trapped in the helical multiple-mirror field into the loss cone of the strong mirror in hotter plasma in strong magnetic field. This threshold can be estimated for the plasma parameters of the GDMT project (Skovorodin et al. 2023) that features 20 T HTSC main mirrors. The ion temperature $T_i=1.39\,{\rm keV}$ gives the ion thermal velocity $V_{Ti}=3.65\times 10^5\,{\rm m}\,{\rm s}^{-1}$. Reasonable estimation of the guiding magnetic field in the helical section with Nb$_3$Sn conductor is $B_z\sim 8\,{\rm T}$, therefore the mirror ratio can be estimated as $R_s\sim 2.5$. It gives the required axial velocity of the magnetic corrugations $V_z\sim 3\times 10^5\,{\rm m}\,{\rm s}^{-1}$. Depending on the corrugation period and the plasma radius in the mirror, it requires a radial electric field of the order of a few kilovolts per centimetre. The problem of inducing fast enough plasma rotation should be addressed in future research of the helical mirrors. On the other hand, the ‘mirror at the exit’ configuration also demonstrates the significant improvement over the configuration with the classical short mirror. This means that helical mirror sections can be inserted between a confinement zone and the main high-field magnetic mirrors. Due to the lower required magnetic field, this type of design reduces the engineering challenges significantly for the helical magnetic section of a future reactor-grade open trap. Definite layout of the mirror combination in the GDMT project also has to be optimised in further research.