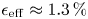1. Introduction
Quasi-isodynamic (QI) stellarators are relevant fusion reactor candidates due to their inherent steady-state operation, and reduced toroidal current, which prevents current-driven instabilities and reduces the Shafranov shift (Helander & Nührenberg Reference Helander and Nührenberg2009; Helander, Geiger & Maaßberg Reference Helander, Geiger and Maaßberg2011; Helander Reference Helander2014). Additionally, if the so-called maximum-J condition is imposed (Rosenbluth Reference Rosenbluth1968), further benefits are expected with respect to turbulent transport, including trapped particle mode stability (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander, Proll & Plunk Reference Helander, Proll and Plunk2013; Helander et al. Reference Helander, Bird, Jenko, Kleiber, Plunk, Proll, Riemann and Xanthopoulos2015; Alcusón et al. Reference Alcusón, Xanthopoulos, Plunk, Helander, Wilms, Turkin, von Stechow and Grulke2020) and some degree of ITG (ion temperature gradient) stabilization (Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). Stellarators have sometimes been considered to be at a disadvantage with respect to tokamaks due to the technical difficulties involved in their construction, but the success of the Wendelstein 7-X experiment has shown that these devices can be built and operated (Pedersen et al. Reference Pedersen, König, Krychowiak, Jakubowski, Baldzuhn, Bozhenkov, Fuchert, Langenberg, Niemann and Zhang2018; Beidler et al. Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Borchardt, Bozhenkov, Brunner and Damm2021), placing the QI stellarator at the forefront of contenders for next-generation stellarator reactor concepts.
Quasi-isodynamic configurations are a subset of omnigenous magnetic fields with poloidally closed contours of the field strength. Omnigenity requires the average radial drift of a trapped particle to vanish:
where $\boldsymbol {v_d}$![]() is the guiding-centre drift velocity and the integration is performed over the bounce time of the trapped-particle orbit (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997; Helander Reference Helander2014). This guarantees radially confined collisionless orbits for trapped particles, which is in general not guaranteed in stellarators. Another subset of omnigenity is the case of quasi-symmetry, for which the intensity of the magnetic field is symmetric when expressed in magnetic coordinates.
is the guiding-centre drift velocity and the integration is performed over the bounce time of the trapped-particle orbit (Hall & McNamara Reference Hall and McNamara1975; Cary & Shasharina Reference Cary and Shasharina1997; Helander Reference Helander2014). This guarantees radially confined collisionless orbits for trapped particles, which is in general not guaranteed in stellarators. Another subset of omnigenity is the case of quasi-symmetry, for which the intensity of the magnetic field is symmetric when expressed in magnetic coordinates.
Finding stellarator configurations consistent with omnigenity is an arduous task that is traditionally achieved through numerical optimization of the plasma boundary shape. The solution space of stellarators is vast, approximately an order of magnitude more degrees of freedom than tokamaks (Boozer Reference Boozer2015), and as a result, optimization is numerically expensive and highly dependent on the choice of good initial points.
The near-axis expansion (NAE) method was originally proposed by Mercier (Reference Mercier1964) and adapted for Boozer coordinates by Garren & Boozer (Reference Garren and Boozer1991). This made it possible to construct stellarators that are omnigenous at least close to the axis without the need of an optimization procedure, as shown in Landreman & Sengupta (Reference Landreman and Sengupta2018) and Landreman, Sengupta & Plunk (Reference Landreman, Sengupta and Plunk2019) for the case of quasi-symmetry, and in Plunk, Landreman & Helander (Reference Plunk, Landreman and Helander2019) and Camacho Mata, Plunk & Jorge (Reference Camacho Mata, Plunk and Jorge2022) for QI fields. We describe the main equations of the NAE formalism in § 2 and use it throughout this work to shed some light into the structure of the QI solution space.
An important aspect of the NAE is the intrinsic parametric nature of the construction. Instead of indicating the shape of the plasma boundary, the input parameters are more closely related to physically relevant parameters of the configuration, like the shape of the magnetic axis, directly contributing to the rotational transform $\iotaslash$![]() and the intensity of the magnetic field along the axis. By carefully choosing these parameters, a low level of neoclassical confinement can be achieved even at considerable distances from the axis, i.e. at low aspect ratios (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). Optimization within these parameters has resulted in remarkably low neoclassical transport, as measured by the effective neoclassical ripple metric ${\epsilon _{\mathrm {eff}}}{}$
and the intensity of the magnetic field along the axis. By carefully choosing these parameters, a low level of neoclassical confinement can be achieved even at considerable distances from the axis, i.e. at low aspect ratios (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). Optimization within these parameters has resulted in remarkably low neoclassical transport, as measured by the effective neoclassical ripple metric ${\epsilon _{\mathrm {eff}}}{}$![]() (Jorge et al. Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022). Boundary optimization using NAE configurations as initial points has also allowed the discovery of novel QI stellarators with excellent fast-particle confinement (Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach and Helander2023). However, these methods have only led to configurations with a small number of field periods ($N{<}3$
(Jorge et al. Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022). Boundary optimization using NAE configurations as initial points has also allowed the discovery of novel QI stellarators with excellent fast-particle confinement (Goodman et al. Reference Goodman, Camacho Mata, Henneberg, Jorge, Landreman, Plunk, Smith, Mackenbach and Helander2023). However, these methods have only led to configurations with a small number of field periods ($N{<}3$![]() ), in stark contrast to traditionally optimized QI configurations, like W7-X, QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006) or Shafranov et al. (Reference Shafranov, Cooper, Heyn, Isaev, Kalyuzhnyj, Kasilov, Kernbichler, Mikhailov, Nemov and Nührenberg2004) with $N=5,6$
), in stark contrast to traditionally optimized QI configurations, like W7-X, QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006) or Shafranov et al. (Reference Shafranov, Cooper, Heyn, Isaev, Kalyuzhnyj, Kasilov, Kernbichler, Mikhailov, Nemov and Nührenberg2004) with $N=5,6$![]() and 9, respectively.
and 9, respectively.
The space of QI configurations has proven to be complex and difficult to explore, as is evident from the tendency of traditional boundary optimizations to get stuck in local minima. The NAE has the potential to help overcome this issue, for example by mapping a suitably defined solution space, as has been successfully done for the space of quasi-symmetric configurations in Landreman (Reference Landreman2022) and Rodriguez, Sengupta & Bhattacharjee (Reference Rodriguez, Sengupta and Bhattacharjee2022, Reference Rodriguez, Sengupta and Bhattacharjee2023). The magnetic axis shape, a three-dimensional curve, is one of the most important parameters for the NAE construction. The helicity of the axis, also called self-linking number, counts the number of times the normal Frenet vector rotates around the axis, and as discussed in Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022) and Landreman & Catto (Reference Landreman and Catto2012), divides the space of symmetric configurations into quasi-axisymmetric and quasi-helical, with the transition between these phases corresponding to the QI case. In § 3 we expand on the definition of helicity, and the particularities of calculating it for the case of QI near-axis configurations. We also discuss the divisions in the solution space due to helicity and the impacts of this division in neoclassical confinement and rotational transform of the configurations.
In § 4 we introduce the possibility of having fractional values of helicity and the conditions required on the curvature of the axis to attain such values. We proceed by showing that stellarator-symmetric configurations consistent with the NAE for QI can be constructed around axes with half-helicity, and we present a two-field-period example with similar properties to the configuration described in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), showing that half-helicity configurations can be as good as their integer-helicity counterparts.
We explore the implications of half-helicity (or more precisely, helicity of $n{+}\tfrac {1}{2}$![]() with $n$
with $n$![]() any integer) in the QI space and show that this fractional helicity is the only one possible for the case of stellarator-symmetric near-axis configurations and corresponds to the transition between zero and integer helicities, making it a smaller solution space than the integer-helicity space. We show in § 7 that searching in this smaller space allows us to find configurations with higher number of field periods and low ${\epsilon _{\mathrm {eff}}}{}$
any integer) in the QI space and show that this fractional helicity is the only one possible for the case of stellarator-symmetric near-axis configurations and corresponds to the transition between zero and integer helicities, making it a smaller solution space than the integer-helicity space. We show in § 7 that searching in this smaller space allows us to find configurations with higher number of field periods and low ${\epsilon _{\mathrm {eff}}}{}$![]() . A five-field-period example is also shown, and the details of the construction parameters’ choice are discussed, including how to reduce elongation of the plasma boundary cross-section.
. A five-field-period example is also shown, and the details of the construction parameters’ choice are discussed, including how to reduce elongation of the plasma boundary cross-section.
2. Near-axis expansion
The properties of a magnetohydrodynamic (MHD) equilibrium can be described in the vicinity of the magnetic axis by performing a Taylor expansion in the parameter $\epsilon = a/R$![]() , the inverse aspect ratio, where $a$
, the inverse aspect ratio, where $a$![]() and $R$
and $R$![]() are the minor and major radius, respectively. This procedure, using Boozer coordinates ($\psi,\theta,\varphi$
are the minor and major radius, respectively. This procedure, using Boozer coordinates ($\psi,\theta,\varphi$![]() ), was shown in Garren & Boozer (Reference Garren and Boozer1991) to allow for the numerical construction of quasi-symmetric configurations, and was extended to consider QI configurations at first order in Plunk et al. (Reference Plunk, Landreman and Helander2019). We restrict our study to the case of first-order, QI, stellarator-symmetric equilibria as described in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).
), was shown in Garren & Boozer (Reference Garren and Boozer1991) to allow for the numerical construction of quasi-symmetric configurations, and was extended to consider QI configurations at first order in Plunk et al. (Reference Plunk, Landreman and Helander2019). We restrict our study to the case of first-order, QI, stellarator-symmetric equilibria as described in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).
This method allows us to directly construct QI equilibria at first order by prescribing the shape of a magnetic axis $x_0$![]() , the intensity of the magnetic field on the axis $B_0$
, the intensity of the magnetic field on the axis $B_0$![]() , the number of field periods $N$
, the number of field periods $N$![]() , two toroidal geometric functions $\alpha (\varphi )$
, two toroidal geometric functions $\alpha (\varphi )$![]() and $d(\varphi )$
and $d(\varphi )$![]() , which are later discussed in more detail, and a distance from the axis at which we desire to construct the equilibrium. In this formalism, the magnetic field intensity is given by
, which are later discussed in more detail, and a distance from the axis at which we desire to construct the equilibrium. In this formalism, the magnetic field intensity is given by
and the plasma boundary is described by
with
Here $\kappa$![]() and $\tau$
and $\tau$![]() are the curvature and torsion of the magnetic axis and the quantity $\sigma (\varphi )$
are the curvature and torsion of the magnetic axis and the quantity $\sigma (\varphi )$![]() can be found by solving
can be found by solving
self-consistently with the rotational transform on axis $\iotaslash$![]() . Here, $\bar {d}(\varphi ) = d(\varphi ) /\kappa ^{s}(\varphi )$
. Here, $\bar {d}(\varphi ) = d(\varphi ) /\kappa ^{s}(\varphi )$![]() , primes denote derivatives with respect to the toroidal Boozer angle $\varphi$
, primes denote derivatives with respect to the toroidal Boozer angle $\varphi$![]() and $G_{0}$
and $G_{0}$![]() and $I_2$
and $I_2$![]() are related to the first non-zero terms of the poloidal and toroidal current functions on axis; $I_2$
are related to the first non-zero terms of the poloidal and toroidal current functions on axis; $I_2$![]() can be assumed to be zero for QI configurations.
can be assumed to be zero for QI configurations.
The function $d(\varphi )$![]() needs to be specified as an input for the construction, but the choice is not entirely free; a set of conditions need to be fulfilled to be consistent with omnigenity and stellarator symmetry. It must vanish at all extrema of the on-axis magnetic field $B_0$
needs to be specified as an input for the construction, but the choice is not entirely free; a set of conditions need to be fulfilled to be consistent with omnigenity and stellarator symmetry. It must vanish at all extrema of the on-axis magnetic field $B_0$![]() :
:
Given how the definition of the boundary depends directly on the quantity $\bar {d}$![]() ((2.3) and (2.4)), the curvature must necessarily have zeros at the same toroidal locations and of the same order as $d$
((2.3) and (2.4)), the curvature must necessarily have zeros at the same toroidal locations and of the same order as $d$![]() , to ensure a smooth plasma boundary. Additionally $d$
, to ensure a smooth plasma boundary. Additionally $d$![]() must be an odd function about $\varphi _{\mathrm {min}}$
must be an odd function about $\varphi _{\mathrm {min}}$![]() , which implies this function will always have derivatives of odd order equal to zero at such points. Then $\kappa$
, which implies this function will always have derivatives of odd order equal to zero at such points. Then $\kappa$![]() must also be zero up to odd order. The simplest case corresponds to both functions having first-order zeros at the minima of $B_0$
must also be zero up to odd order. The simplest case corresponds to both functions having first-order zeros at the minima of $B_0$![]() .
.
Finally, the last ingredient for constructing a near-axis QI equilibrium is the function $\alpha (\varphi )$![]() . Just like $d$
. Just like $d$![]() , it must be specified in a way consistent with omnigenity, albeit as shown in Plunk et al. (Reference Plunk, Landreman and Helander2019) this condition being not compatible with a periodic plasma boundary. For this reason, omnigenity must be broken around the maxima of $B_0$
, it must be specified in a way consistent with omnigenity, albeit as shown in Plunk et al. (Reference Plunk, Landreman and Helander2019) this condition being not compatible with a periodic plasma boundary. For this reason, omnigenity must be broken around the maxima of $B_0$![]() . The method we use is that described in § 4 of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), with
. The method we use is that described in § 4 of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022), with

where $m$![]() is the axis helicity, to which the next section is devoted, and $k$
is the axis helicity, to which the next section is devoted, and $k$![]() is an integer that controls the size of the region in which the omnigenity conditions are fulfilled; increasing $k$
is an integer that controls the size of the region in which the omnigenity conditions are fulfilled; increasing $k$![]() results in a larger toroidal domain in which $\alpha$
results in a larger toroidal domain in which $\alpha$![]() is omnigenous but at the cost of a sharp behaviour around the maxima to maintain a periodic behaviour. The superscript $i$
is omnigenous but at the cost of a sharp behaviour around the maxima to maintain a periodic behaviour. The superscript $i$![]() is an integer number labelling the minima of $B_0$
is an integer number labelling the minima of $B_0$![]() ; given how we are just considering a minimum per field period, this is equivalent to the field-period label.
; given how we are just considering a minimum per field period, this is equivalent to the field-period label.
3. Helicity
The geometric properties of a three-dimensional space curve $\boldsymbol {r}(\ell )$![]() can be described by the Frenet–Serret vectors $(\boldsymbol {t},\boldsymbol {n},\boldsymbol {b})$
can be described by the Frenet–Serret vectors $(\boldsymbol {t},\boldsymbol {n},\boldsymbol {b})$![]() . These orthogonal unitary vectors, named tangent, normal and binormal, respectively, are defined by
. These orthogonal unitary vectors, named tangent, normal and binormal, respectively, are defined by

and are related to the curvature and torsion ($\kappa, \tau$![]() ) of the curve through the Frenet–Serret formulas:
) of the curve through the Frenet–Serret formulas:

This frame plays an important role in the construction of exactly omnigenous stellarators at first order around the magnetic axis as described in Landreman & Sengupta (Reference Landreman and Sengupta2018) and Plunk et al. (Reference Plunk, Landreman and Helander2019), given that it is used to describe the plasma boundary as seen in (2.2).
One interesting property of a magnetic axis described using this apparatus is the so-called helicity, $M$![]() , the number of times the normal vector $\boldsymbol {n(\ell )}$
, the number of times the normal vector $\boldsymbol {n(\ell )}$![]() rotates poloidally around the axis after one toroidal turn. In this work we often refer to the per-field-period helicity $m=M/N$
rotates poloidally around the axis after one toroidal turn. In this work we often refer to the per-field-period helicity $m=M/N$![]() , for example, in (2.7), the definition of the $\alpha$
, for example, in (2.7), the definition of the $\alpha$![]() function. In the case of quasi-symmetric configurations, the helicity effectively divides the space of solutions as shown in Landreman & Sengupta (Reference Landreman and Sengupta2018) and Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022): a value of $M=0$
function. In the case of quasi-symmetric configurations, the helicity effectively divides the space of solutions as shown in Landreman & Sengupta (Reference Landreman and Sengupta2018) and Rodriguez et al. (Reference Rodriguez, Sengupta and Bhattacharjee2022): a value of $M=0$![]() corresponds to axisymmetric configurations while an integer value of $M\neq 0$
corresponds to axisymmetric configurations while an integer value of $M\neq 0$![]() corresponds to quasi-helically symmetric solutions.
corresponds to quasi-helically symmetric solutions.
For QI configurations, which are the main focus of this work, calculating helicity requires extra considerations. As shown in the previous section, points of zero curvature are required in magnetic axes consistent with quasi-isodynamicity in the near-axis formalism. But we can see from the first equation in (3.2) that $\kappa = 0$![]() results in an undefined normal vector. In the presence of points of first-order zero curvature,Footnote 1 the Frenet frame undergoes a jump-like rotation which makes the frame, specifically the normal and binormal vectors, non-continuous (Aicardi Reference Aicardi2000), as can be seen in figure 1(a). This discontinuity can be alleviated by using the signed curvature $\kappa ^{s}= s \kappa$
results in an undefined normal vector. In the presence of points of first-order zero curvature,Footnote 1 the Frenet frame undergoes a jump-like rotation which makes the frame, specifically the normal and binormal vectors, non-continuous (Aicardi Reference Aicardi2000), as can be seen in figure 1(a). This discontinuity can be alleviated by using the signed curvature $\kappa ^{s}= s \kappa$![]() , where $s = \pm 1$
, where $s = \pm 1$![]() changes at each point of odd-order zeros of curvature. In this new frame (Carroll, Köse & Sterling Reference Carroll, Köse and Sterling2013), the sign of the traditional Frenet normal and binormal vectors $\boldsymbol {n}(\ell ),\boldsymbol {t}(\ell )$
changes at each point of odd-order zeros of curvature. In this new frame (Carroll, Köse & Sterling Reference Carroll, Köse and Sterling2013), the sign of the traditional Frenet normal and binormal vectors $\boldsymbol {n}(\ell ),\boldsymbol {t}(\ell )$![]() also changes when $\kappa = 0$
also changes when $\kappa = 0$![]() resulting in a continuous frame as shown in figure 1(b). Helicity for QI configurations is hence calculated using this modified Frenet frame to avoid any discontinuities in the plasma boundary shape.
resulting in a continuous frame as shown in figure 1(b). Helicity for QI configurations is hence calculated using this modified Frenet frame to avoid any discontinuities in the plasma boundary shape.

Figure 1. (a) Unsigned Frenet frame and (b) signed Frenet frame for a two-field-period axis. Side view and top view are shown. Normal $\hat {n}$![]() and binormal $\hat {b}$
and binormal $\hat {b}$![]() vectors are shown in red and blue, respectively. We can see that the discontinuities in the frame are alleviated when using the signed curvature, $\kappa ^s$
vectors are shown in red and blue, respectively. We can see that the discontinuities in the frame are alleviated when using the signed curvature, $\kappa ^s$![]() .
.
As in the case of quasi-symmetry, helicity also effectively divides the space of QI near-axis solutions as can be seen in figure 2. Here, the helicity value for 1156 one-field-period, near-axis configurations is shown, each for a different axis shape while keeping the rest of the near-axis parameters constant. All these configurations have the same axis radial component
which ensures two zeros of curvature are present at the minima and maxima of the magnetic field on axis. The vertical component of the axis shape is different for each configurations and chosen as
Each square in figure 2 corresponds to a configuration with $z_s(1)$![]() ranging from 0 to 0.8 and $z_s(2)$
ranging from 0 to 0.8 and $z_s(2)$![]() from $-$
from $-$![]() 0.425 to 0.4, constructed using the near-axis method described in § 2. The aspect ratio is set to $A=20$
0.425 to 0.4, constructed using the near-axis method described in § 2. The aspect ratio is set to $A=20$![]() , the function $\alpha (\varphi )$
, the function $\alpha (\varphi )$![]() is described by (2.7) with $k=2$
is described by (2.7) with $k=2$![]() , the magnetic field on axis is $B_0 = 1+0.15\cos (\varphi )$
, the magnetic field on axis is $B_0 = 1+0.15\cos (\varphi )$![]() and $d = 0.73 \kappa ^s$
and $d = 0.73 \kappa ^s$![]() .
.

Figure 2. Space of one-field-period near-axis QI configurations and their helicity values. Each square corresponds to a near-axis QI configuration and its helicity value, green for $m=1$![]() and blue $m=0$
and blue $m=0$![]() . The solid lines show the transition between helicity regions and correspond to second-order zeros of curvature at $\varphi _{\mathrm {min}}$
. The solid lines show the transition between helicity regions and correspond to second-order zeros of curvature at $\varphi _{\mathrm {min}}$![]() (upper line) and $\varphi _{\mathrm {max}}$
(upper line) and $\varphi _{\mathrm {max}}$![]() (lower line).
(lower line).
The solid black lines in figure 2, bounding each helicity region, can be obtained analytically and correspond to the values of $z_s(1){-}z_s(2)$![]() that result in second-order zeros of curvature, i.e. ${\textrm {d}\kappa }/{\textrm {d}\phi }|_{\varphi }=0$
that result in second-order zeros of curvature, i.e. ${\textrm {d}\kappa }/{\textrm {d}\phi }|_{\varphi }=0$![]() , at $\varphi _{\mathrm {min}}$
, at $\varphi _{\mathrm {min}}$![]() (upper line) and $\varphi _{\mathrm {max}}$
(upper line) and $\varphi _{\mathrm {max}}$![]() (lower line). The analytical derivation is shown in Appendix A.
(lower line). The analytical derivation is shown in Appendix A.
It is clear from figure 2 that the space of QI solutions is divided into subregions by the helicity of the magnetic axis. But perhaps more surprising is the fact that this division is also present when calculating the effective ripple of each configuration in this space, as shown in figure 3. Here, each of the plasma boundary shapes of the configurations in figure 2 is used to solve for a MHD equilibrium using the VMEC code (Hirshman & Whitson Reference Hirshman and Whitson1983), and $\epsilon _{\mathrm {eff}}$![]() , the effective ripple, is calculated as described in Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003). The maximum value of this quantity is shown colour-coded in the figure. The white squares correspond to configurations for which VMEC could not find an equilibrium consistent with the provided plasma boundary. Once again, the division between regions of helicity is observed, and consistently lower values of $\epsilon _{\mathrm {eff}}$
, the effective ripple, is calculated as described in Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003). The maximum value of this quantity is shown colour-coded in the figure. The white squares correspond to configurations for which VMEC could not find an equilibrium consistent with the provided plasma boundary. Once again, the division between regions of helicity is observed, and consistently lower values of $\epsilon _{\mathrm {eff}}$![]() and rotational transform $\iotaslash$
and rotational transform $\iotaslash$![]() are found for zero-helicity configurations. The intensity of $B$
are found for zero-helicity configurations. The intensity of $B$![]() on the boundary for a configuration from each region is also shown, but constructed at a smaller aspect ratio $A=10$
on the boundary for a configuration from each region is also shown, but constructed at a smaller aspect ratio $A=10$![]() , to exemplify these differences. On the left-hand side, one corresponding to an $m=1$
, to exemplify these differences. On the left-hand side, one corresponding to an $m=1$![]() axis, with a maximum $\epsilon _{\mathrm {eff}}=1.1\,\%$
axis, with a maximum $\epsilon _{\mathrm {eff}}=1.1\,\%$![]() and rotational transform $\iotaslash = 0.4351$
and rotational transform $\iotaslash = 0.4351$![]() ; while the configuration with $m=0$
; while the configuration with $m=0$![]() has a substantially lower $\epsilon _{\mathrm {eff}}=0.35\,\%$
has a substantially lower $\epsilon _{\mathrm {eff}}=0.35\,\%$![]() and $\iotaslash = 0.0587$
and $\iotaslash = 0.0587$![]() .
.

Figure 3. Space of one-field-period, $A=20$![]() , near-axis QI configurations. Parameters $z_s(1)$
, near-axis QI configurations. Parameters $z_s(1)$![]() and $z_s(2)$
and $z_s(2)$![]() correspond to the parameters of the cylindrical Fourier representation of the axis (3.4). Each square is a near-axis configuration constructed with the parameters described in § 3. Colour coded is the maximum value of the effective ripple ${\epsilon _{\mathrm {eff}}}{}$
correspond to the parameters of the cylindrical Fourier representation of the axis (3.4). Each square is a near-axis configuration constructed with the parameters described in § 3. Colour coded is the maximum value of the effective ripple ${\epsilon _{\mathrm {eff}}}{}$![]() . Black solid lines correspond to the transition between regions with helicity 0 and 1. One configuration of each region is shown as an example of the properties in that space; the last closed surface and the intensity of the magnetic field on the boundary are shown. Zero-helicity configurations have lower ${\epsilon _{\mathrm {eff}}}{}$
. Black solid lines correspond to the transition between regions with helicity 0 and 1. One configuration of each region is shown as an example of the properties in that space; the last closed surface and the intensity of the magnetic field on the boundary are shown. Zero-helicity configurations have lower ${\epsilon _{\mathrm {eff}}}{}$![]() but also lower rotational transform than their $m=1$
but also lower rotational transform than their $m=1$![]() counterparts.
counterparts.
Configurations with $m=1$![]() and remarkable low values of $\epsilon _{\mathrm {eff}}$
and remarkable low values of $\epsilon _{\mathrm {eff}}$![]() can be found as shown in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022) for one field period, but it requires a significant effort in choosing the initial parameters. The lower values of effective ripple observed in the zero-helicity configurations suggest that less effort might be necessary in this region of the parameter space.
can be found as shown in Jorge et al. (Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Camacho Mata and Helander2022) for one field period, but it requires a significant effort in choosing the initial parameters. The lower values of effective ripple observed in the zero-helicity configurations suggest that less effort might be necessary in this region of the parameter space.
Helicity seems to play an important role in the near-axis QI space. Although the integer-helicity space seems to correlate low rotational transform and low $\epsilon _{\mathrm {eff}}$![]() , this occurs because helicity is directly related to the integrated torsion of the magnetic axis, which is an important mechanism for rotational transform generation as discussed in Helander (Reference Helander2014). A more in-depth discussion about the relation between torsion and rotational transform in the presence of a discontinuous Frenet frame, without using the signed curvature correction, can be found in Pfefferlé et al. (Reference Pfefferlé, Gunderson, Hudson and Noakes2018). Optimized examples of QI configurations with low $\epsilon _{\mathrm {eff}}$
, this occurs because helicity is directly related to the integrated torsion of the magnetic axis, which is an important mechanism for rotational transform generation as discussed in Helander (Reference Helander2014). A more in-depth discussion about the relation between torsion and rotational transform in the presence of a discontinuous Frenet frame, without using the signed curvature correction, can be found in Pfefferlé et al. (Reference Pfefferlé, Gunderson, Hudson and Noakes2018). Optimized examples of QI configurations with low $\epsilon _{\mathrm {eff}}$![]() and higher per-field-period rotational transform exist. The exploration of such examples may shed light light on novel ways of generating near-axis equilibria with higher $N$
and higher per-field-period rotational transform exist. The exploration of such examples may shed light light on novel ways of generating near-axis equilibria with higher $N$![]() and small $\epsilon _\textrm {eff}$
and small $\epsilon _\textrm {eff}$![]() .
.
4. Half-helicity
In the previous section, we restricted ourselves to the case of integer helicity, implying that the only case with less than complete rotation of the normal is the zero-helicity case. However, it is also possible to construct curves with fractional values of per-field-period helicity. In fact, such behaviour is exhibited by the magnetic axis of QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006), a QI stellarator found through numerical optimization. This configuration has poloidally closed contours of the magnetic field close to the axis and an effective ripple profile that increases radially, making it more similar to a near-axis QI configuration than W7-X.
Although QIPC's magnetic axis does not have points of exactly zero curvature at the extrema of $B_0$![]() , the curvature does reach relatively small values, and its signed Frenet frame behaves in a similar way to near-axis configurations, having a flip at points where the magnetic field on axis has its minimum. Figure 4 shows this axis together with the normal and binormal vectors associated with its signed Frenet frame, the change in sign being applied at the position of the minima of $B_0$
, the curvature does reach relatively small values, and its signed Frenet frame behaves in a similar way to near-axis configurations, having a flip at points where the magnetic field on axis has its minimum. Figure 4 shows this axis together with the normal and binormal vectors associated with its signed Frenet frame, the change in sign being applied at the position of the minima of $B_0$![]() . As we can see from the figure, the normal vector does not complete a whole rotation around the axis each field period;instead the normal vector seems to complete exactly a half-rotation, ending at the opposite direction to that which it started at the beginning of the period. We note that all QI designs found in the past by numerical optimization share this half-rotation feature ($m=1/2$
. As we can see from the figure, the normal vector does not complete a whole rotation around the axis each field period;instead the normal vector seems to complete exactly a half-rotation, ending at the opposite direction to that which it started at the beginning of the period. We note that all QI designs found in the past by numerical optimization share this half-rotation feature ($m=1/2$![]() ). However, this case has not been considered when constructing near-axis QI configurations in the literature. As we show, it allows us to access a region in the solution space where good confinement can be achieved with a relatively high number of field periods.
). However, this case has not been considered when constructing near-axis QI configurations in the literature. As we show, it allows us to access a region in the solution space where good confinement can be achieved with a relatively high number of field periods.

Figure 4. Unsigned and signed Frenet frame for the magnetic axis of QIPC, a six-field-period QI optimized configuration (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006). Green circles indicate the toroidal locations of the maxima of $B_0$![]() , marking the beginning/end of a magnetic field period. Green diamonds indicate the minima of $B_0$
, marking the beginning/end of a magnetic field period. Green diamonds indicate the minima of $B_0$![]() . Normal and binormal Frenet vectors are shown in red and blue lines, respectively. A discontinuity in the frame at minima of $B_0$
. Normal and binormal Frenet vectors are shown in red and blue lines, respectively. A discontinuity in the frame at minima of $B_0$![]() is evident in the signed frame from the direction change of the normal vector. This discontinuity is alleviated when using the signed frame and is transferred to the maxima of $B_0$
is evident in the signed frame from the direction change of the normal vector. This discontinuity is alleviated when using the signed frame and is transferred to the maxima of $B_0$![]() .
.
Let us now discuss the particularities of constructing a magnetic axis with $m=1/2$![]() . We know a magnetic axis consistent with omnigenity needs to have points of zero curvature at all minima and maxima of the magnetic field (Plunk et al. Reference Plunk, Landreman and Helander2019), which requires calculating helicity in the signed Frenet frame, since the axis helicity is otherwise not well defined. Additionally, for a curve to have half-helicity, we require the normal vector to perform half a rotation per field period. This situation is not consistent with first-order zeros of curvature at both $\varphi _{\mathrm {min}}$
. We know a magnetic axis consistent with omnigenity needs to have points of zero curvature at all minima and maxima of the magnetic field (Plunk et al. Reference Plunk, Landreman and Helander2019), which requires calculating helicity in the signed Frenet frame, since the axis helicity is otherwise not well defined. Additionally, for a curve to have half-helicity, we require the normal vector to perform half a rotation per field period. This situation is not consistent with first-order zeros of curvature at both $\varphi _{\mathrm {min}}$![]() and $\varphi _{\mathrm {max}}$
and $\varphi _{\mathrm {max}}$![]() , at least not for the case of analytic stellarator-symmetric axis curves, which can be seen by re-examining the expansion near zero-curvature points, as follows.
, at least not for the case of analytic stellarator-symmetric axis curves, which can be seen by re-examining the expansion near zero-curvature points, as follows.
As shown in § 3 of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) and discussed after (2.6), omnigenity conditions imposed in the NAE for stellarator-symmetric configurations require odd-order zeros of $\kappa$![]() at the minima of $B_0$
at the minima of $B_0$![]() . If the axis is described as a Fourier series on the cylindrical $R$
. If the axis is described as a Fourier series on the cylindrical $R$![]() and $z$
and $z$![]() coordinates,
coordinates,


Then having a point of zero curvature at first order requires $({\textrm {d}^{2}x}/{\textrm {d}\phi ^2})\cdot \hat {R} = 0$![]() at such a point, as shown in Appendix A (appendix II in Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022), which given the definition of $\boldsymbol {n}$
at such a point, as shown in Appendix A (appendix II in Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022), which given the definition of $\boldsymbol {n}$![]() (3.1), is equivalent to the condition
(3.1), is equivalent to the condition
at $\varphi = \varphi _{\mathrm {min}}$![]() . The case $m=1/2$
. The case $m=1/2$![]() corresponds to the normal vector performing a ${\rm \pi}$
corresponds to the normal vector performing a ${\rm \pi}$![]() -rotation in the $\hat {R}$
-rotation in the $\hat {R}$![]() –$\hat {z}$
–$\hat {z}$![]() plane per field period. Hence, after half a period, at $\varphi = \varphi _{\mathrm {max}}$
plane per field period. Hence, after half a period, at $\varphi = \varphi _{\mathrm {max}}$![]() , a ${{\rm \pi} }/{2}$
, a ${{\rm \pi} }/{2}$![]() -rotation would require the normal vector to point in the radial direction:
-rotation would require the normal vector to point in the radial direction:
As shown above and explained in greater detail in Appendix A, odd-order zeros of curvature are generally inconsistent with a normal vector having a component in the radial direction, but consistent with even-order zeros. We can intuitively visualize each increase in the order of the zeros of curvature as introducing a flip on the Frenet frame, hence the need for different behaviour of $\kappa$![]() at the minima and maxima of $B_0$
at the minima and maxima of $B_0$![]() to preserve a discontinuity of the frame that is not corrected by the sign change described in the previous section. We can then construct half-helicity closed curves, just by requiring a first-order zero of curvature at $\varphi = \varphi _{\mathrm {min}}$
to preserve a discontinuity of the frame that is not corrected by the sign change described in the previous section. We can then construct half-helicity closed curves, just by requiring a first-order zero of curvature at $\varphi = \varphi _{\mathrm {min}}$![]() and a second-order zero at $\varphi = \varphi _{\mathrm {max}}$
and a second-order zero at $\varphi = \varphi _{\mathrm {max}}$![]() . We note that these arguments rely on continuity of the derivatives of the curve, which can safely be assumed for curves constructed by Fourier series, but need not be the case more generally, as with curves found by solving Frenet–Serret equations directly. We also remark that, when assuming stellarator symmetry as is done in this work, the only helicities possible are either integer or half-helicity, since this is the only fractional helicity allowing for points of zero curvature and continuity of the plasma boundary. Different fractional helicities might be possible for certain non-stellarator-symmetric configurations, but this issue needs to be explored further.
. We note that these arguments rely on continuity of the derivatives of the curve, which can safely be assumed for curves constructed by Fourier series, but need not be the case more generally, as with curves found by solving Frenet–Serret equations directly. We also remark that, when assuming stellarator symmetry as is done in this work, the only helicities possible are either integer or half-helicity, since this is the only fractional helicity allowing for points of zero curvature and continuity of the plasma boundary. Different fractional helicities might be possible for certain non-stellarator-symmetric configurations, but this issue needs to be explored further.
Following the same procedure described in Appendix A, we perform a local expansion of a stellarator-symmetric magnetic axis described by (4.1) and (4.2), and impose conditions on the curvature of such an axis, which we can transform into conditions for the Fourier coefficients $R_{c}(n)$![]() and $z_{s}(n)$
and $z_{s}(n)$![]() . The local condition for having first-order zeros of curvature is
. The local condition for having first-order zeros of curvature is
where $R_n$![]() and $z_n$
and $z_n$![]() denote the $n$
denote the $n$![]() th derivatives with respect to $\phi$
th derivatives with respect to $\phi$![]() . For a second-order zero of $\kappa$
. For a second-order zero of $\kappa$![]() , we additionally need to fulfil
, we additionally need to fulfil
We can apply the previous conditions to a truncated Fourier representation in order to obtain conditions on its coefficients that can be used to construct curves with the curvature properties required to obtain a half-helicity behaviour. We can consider, for example, the family of curves

Applying condition (4.5) at $\phi =2{\rm \pi} /N$![]() and both the previous condition and (4.6) to $\phi =0$
and both the previous condition and (4.6) to $\phi =0$![]() returns the following restrictions on the Fourier coefficients necessary to construct curves with half-helicity per field period:
returns the following restrictions on the Fourier coefficients necessary to construct curves with half-helicity per field period:
An axis constructed using this method is shown in figure 5, where the parameters were chosen as $N=2$![]() , $R_c(3) = 5 {\times } 10^{-3}$
, $R_c(3) = 5 {\times } 10^{-3}$![]() , $z_s(2) = 3 {\times } 10^{-2}$
, $z_s(2) = 3 {\times } 10^{-2}$![]() and $z_s(3) = 1.5 {\times } 10^{-3}$
and $z_s(3) = 1.5 {\times } 10^{-3}$![]() . We can see the rotation of the signed normal and binormal vectors has the expected behaviour, with one jump per field period.
. We can see the rotation of the signed normal and binormal vectors has the expected behaviour, with one jump per field period.

Figure 5. Signed Frenet frame for a half-helicity two-field-period curve. Note the discontinuity that remains at the location where the magnetic field strength is taken to be maximal, where the normal vector points in the radial direction.
5. Constructing half-helicity near-axis stellarators
Now we can proceed to use this axis to construct a near-axis configuration, as described in § 2. A natural question to ask is whether the discontinuity in the signed Frenet frame at maxima of the magnetic field, required for half-helicity magnetic axes, has a detrimental effect on the continuity of the plasma boundary. We confirm that the formalism developed in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) is valid for fractional helicity and results in continuous plasma boundaries.
We know from the previous section that the signed Frenet frame, specifically the normal and binormal vectors are discontinuous at maxima of $B_{0}$![]() for half-helicity configurations. Given how the plasma boundary of a NAE equilibrium is constructed using (2.2),
for half-helicity configurations. Given how the plasma boundary of a NAE equilibrium is constructed using (2.2),
it would be natural to assume the discontinuity of $\boldsymbol {n}^{s}$![]() and $\boldsymbol {b}^{s}$
and $\boldsymbol {b}^{s}$![]() translates into a discontinuity of the boundary shape, but this is only true if $X_1$
translates into a discontinuity of the boundary shape, but this is only true if $X_1$![]() and $Y_1$
and $Y_1$![]() are continuous. Let us analyse the behaviour of this first-order correction to the plasma boundary:
are continuous. Let us analyse the behaviour of this first-order correction to the plasma boundary:
The quantity $\bar {d} = d(\varphi )/\kappa ^{s}$![]() is, by definition, constructed to be symmetric and continuous at every point, in particular at $\varphi _{\mathrm {min}}$
is, by definition, constructed to be symmetric and continuous at every point, in particular at $\varphi _{\mathrm {min}}$![]() and $\varphi _{\mathrm {max}}$
and $\varphi _{\mathrm {max}}$![]() as discussed in § 2 and evident from (2.6) (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). The magnetic field on axis $B_0(\varphi )$
as discussed in § 2 and evident from (2.6) (Camacho Mata et al. Reference Camacho Mata, Plunk and Jorge2022). The magnetic field on axis $B_0(\varphi )$![]() is always continuous, also at points where the signed Frenet frame is discontinuous. Hence, any possible discontinuity in $X_1$
is always continuous, also at points where the signed Frenet frame is discontinuous. Hence, any possible discontinuity in $X_1$![]() and $Y_1$
and $Y_1$![]() is going to depend on the behaviour of $\alpha (\varphi )$
is going to depend on the behaviour of $\alpha (\varphi )$![]() , given by (2.7), reproduced here:
, given by (2.7), reproduced here:

Note the first term ensures that the magnetic perturbation is approximately in phase at two bounce points (omnigenity), while the final term is designed to break this criterion away from minima of the field, while ensuring the boundary retains the correct periodicity; see Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) for more details. For half-helicity curves, $m=1/2$![]() , and let us consider the first field period, which means $i=1$
, and let us consider the first field period, which means $i=1$![]() and the minimum of $B$
and the minimum of $B$![]() is located at $\varphi _{\mathrm {min}}^{i}={\rm \pi} /N$
is located at $\varphi _{\mathrm {min}}^{i}={\rm \pi} /N$![]() . Now let us calculate the value that the $\alpha$
. Now let us calculate the value that the $\alpha$![]() -function takes at two consecutive maxima of $B$
-function takes at two consecutive maxima of $B$![]() , i.e. the beginning and end of a field period, corresponding to $\varphi ^{1}_{\mathrm {max}}=0$
, i.e. the beginning and end of a field period, corresponding to $\varphi ^{1}_{\mathrm {max}}=0$![]() and $\varphi ^{2}_{\mathrm {max}}=2{\rm \pi} /N$
and $\varphi ^{2}_{\mathrm {max}}=2{\rm \pi} /N$![]() :
:


We can see that for $m=1/2$![]() the function increases by ${\rm \pi}$
the function increases by ${\rm \pi}$![]() per field period, contrary to the $2{\rm \pi}$
per field period, contrary to the $2{\rm \pi}$![]() -periodicity necessary in the integer-helicity curves. Now let us see the impact this has on the functions $X_1$
-periodicity necessary in the integer-helicity curves. Now let us see the impact this has on the functions $X_1$![]() and $Y_1$
and $Y_1$![]() describing the plasma boundary, (2.3) and (2.4):
describing the plasma boundary, (2.3) and (2.4):


As shown above, the boundary components $X_1$![]() and $Y_1$
and $Y_1$![]() are discontinuous at maxima of $B_{0}$
are discontinuous at maxima of $B_{0}$![]() . This discontinuity is, necessarily, of the same type as that of the Frenet frame; continuity of the coordinate mapping (2.2) is thus achieved despite a discontinuous signed Frenet frame. Now we can use the formalism developed in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) to construct a magnetic configuration that is QI at first order, using a half-helicity magnetic axis.
. This discontinuity is, necessarily, of the same type as that of the Frenet frame; continuity of the coordinate mapping (2.2) is thus achieved despite a discontinuous signed Frenet frame. Now we can use the formalism developed in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) to construct a magnetic configuration that is QI at first order, using a half-helicity magnetic axis.
5.1. A two-field-period half-helicity near-axis stellarator
Let us now proceed to show an example of a two-field-period configuration constructed around a half-helicity magnetic axis:
This axis was constructed to have $m=1/2$![]() as described in § 4, and the values of the near-axis parameters were chosen such that the corresponding VMEC equilibrium has small $\epsilon _{\mathrm {eff}}$
as described in § 4, and the values of the near-axis parameters were chosen such that the corresponding VMEC equilibrium has small $\epsilon _{\mathrm {eff}}$![]() on its boundary, as discussed below. The shape of this magnetic axis, together with its signed Frenet frame, and curvature and torsion profiles are shown in figure 6. We can observe the expected curvature behaviour for half-helicity: a first-order zero at half-period and second-order zeros at the end/beginning of the period.
on its boundary, as discussed below. The shape of this magnetic axis, together with its signed Frenet frame, and curvature and torsion profiles are shown in figure 6. We can observe the expected curvature behaviour for half-helicity: a first-order zero at half-period and second-order zeros at the end/beginning of the period.

Figure 6. (a) Two-field-period half-helicity magnetic axis described by expressions (5.10) and (5.11). The normal and binormal vectors are shown. The discontinuity of the signed Frenet frame is evident at the beginning/end of the period. (b) Curvature (solid) and torsion (dashed) per-field-period profiles of the axis. Note the first-order zero of curvature at $\phi = {\rm \pi}/ N$![]() and second-order zeros at $\phi = 0, 2{\rm \pi} /N$
and second-order zeros at $\phi = 0, 2{\rm \pi} /N$![]() , necessary to achieve values of helicity $m=1/2$
, necessary to achieve values of helicity $m=1/2$![]() .
.
The intensity of the magnetic field on this axis must also be specified and was chosen as
which, as required by the near-axis formalism, has extrema at points where the curvature of the magnetic axis is zero. Another parameter playing an important role in the quality of the solutions, specifically in their elongation and maximum values of $\epsilon _{\mathrm {eff}}$![]() , is the function $d(\varphi )$
, is the function $d(\varphi )$![]() . It was chosen to be proportional to the curvature of the axis as $d=d_{\kappa }\kappa ^s$
. It was chosen to be proportional to the curvature of the axis as $d=d_{\kappa }\kappa ^s$![]() , with
, with
This particular form of $d(\varphi )$![]() , inversely proportional to $B_0$
, inversely proportional to $B_0$![]() , is useful for controlling elongation, and here helps flatten the elongation profile, i.e. reduce its variation in $\varphi$
, is useful for controlling elongation, and here helps flatten the elongation profile, i.e. reduce its variation in $\varphi$![]() , resulting in smaller maximum elongations than using a constant $\bar {d}$
, resulting in smaller maximum elongations than using a constant $\bar {d}$![]() choice.Footnote 2 It is important to remember the elongation dependence on $\bar {d}$
choice.Footnote 2 It is important to remember the elongation dependence on $\bar {d}$![]() is complicated and includes other quantities of the near-axis construction, making it difficult to predict which combination of parameters will result in a desired elongation behaviour. The freedom in $\bar {d}$
is complicated and includes other quantities of the near-axis construction, making it difficult to predict which combination of parameters will result in a desired elongation behaviour. The freedom in $\bar {d}$![]() , however, actually allows more control of the elongation profile, as compared with quasi-symmetric configurations where it must be constant; this is demonstrated in § 7.
, however, actually allows more control of the elongation profile, as compared with quasi-symmetric configurations where it must be constant; this is demonstrated in § 7.
The $\alpha$![]() function is defined as in (2.7), with $k=2$
function is defined as in (2.7), with $k=2$![]() chosen for this configuration. A near-axis solution is constructed using the aforementioned parameters at an aspect ratio $A=\sqrt {{\overline {B_{0}}}/{2}}({R_c(0)}/{\epsilon })=10$
chosen for this configuration. A near-axis solution is constructed using the aforementioned parameters at an aspect ratio $A=\sqrt {{\overline {B_{0}}}/{2}}({R_c(0)}/{\epsilon })=10$![]() , where $\overline {B_0}$
, where $\overline {B_0}$![]() is the average value of $B_0$
is the average value of $B_0$![]() . The boundary is converted to cylindrical coordinates using the method described in § 4.1 of Landreman et al. (Reference Landreman, Sengupta and Plunk2019), which results in elliptical cross-sections as shown in figure 7. This plasma boundary is then used to calculate a MHD equilibrium using the VMEC code. The intensity of the magnetic field on the last-closed flux surface is depicted in figure 8, which shows, even at this small aspect ratio, the behaviour expected for a QI configuration, with poloidally closing contours of $|B|$
. The boundary is converted to cylindrical coordinates using the method described in § 4.1 of Landreman et al. (Reference Landreman, Sengupta and Plunk2019), which results in elliptical cross-sections as shown in figure 7. This plasma boundary is then used to calculate a MHD equilibrium using the VMEC code. The intensity of the magnetic field on the last-closed flux surface is depicted in figure 8, which shows, even at this small aspect ratio, the behaviour expected for a QI configuration, with poloidally closing contours of $|B|$![]() . These contours in Boozer coordinates are shown in figure 9. As expected, the contours look ‘more QI’ the closer we look to the axis, in the sense of having a greater degree of poloidal closure, as well as fewer island defects.
. These contours in Boozer coordinates are shown in figure 9. As expected, the contours look ‘more QI’ the closer we look to the axis, in the sense of having a greater degree of poloidal closure, as well as fewer island defects.

Figure 7. (a) Cross-sections of the two-field-period configuration shown in figure 8 at different toroidal values. (b) Elongation toroidal profile for the same configuration.

Figure 8. Magnetic field intensity in the plasma boundary for a two-field-period half-helicity configuration. (a) Side view and (b) top view.

Figure 9. Contours of magnetic field intensity for the configuration in § 5.1 at $s=0.1$![]() (a), $s=0.5$
(a), $s=0.5$![]() (b) and $s=1$
(b) and $s=1$![]() (c). The poloidally closed contours of $B$
(c). The poloidally closed contours of $B$![]() , characteristic of QI configurations, degrade with distance from the axis.
, characteristic of QI configurations, degrade with distance from the axis.
The resulting configuration has maximum elongation under $5.5$![]() and a dependence on $\phi$
and a dependence on $\phi$![]() as shown in figure 7. Elongation here is taken at $\phi = \textrm {constant}$
as shown in figure 7. Elongation here is taken at $\phi = \textrm {constant}$![]() in real space, and calculated as the ratio between the maximum and minimum distances from the axis on the resulting cross-section. One of the interesting properties of half-helicity configurations is the higher values of rotational transform they can achieve compared with zero-helicity cases due to the fact that the axis curves have higher values of integrated torsion. Here, a rotational transform spanning from $\iotaslash = 0.351$
in real space, and calculated as the ratio between the maximum and minimum distances from the axis on the resulting cross-section. One of the interesting properties of half-helicity configurations is the higher values of rotational transform they can achieve compared with zero-helicity cases due to the fact that the axis curves have higher values of integrated torsion. Here, a rotational transform spanning from $\iotaslash = 0.351$![]() to $0.367$
to $0.367$![]() is found for the VMEC equilibria as seen in figure 10.
is found for the VMEC equilibria as seen in figure 10.

Figure 10. Rotational transform profile for the two-field-period half-helicity configuration.
The effective ripple, $\epsilon _{\mathrm {eff}}$![]() , is a proxy often used to estimate neoclassical transport in the $1/\nu$
, is a proxy often used to estimate neoclassical transport in the $1/\nu$![]() regime in stellarators. We have calculated it as described in Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003) for 16 radial points. A maximum value of $\epsilon _{\mathrm {eff}}=1\,\%$
regime in stellarators. We have calculated it as described in Drevlak et al. (Reference Drevlak, Heyn, Kalyuzhnyj, Kasilov, Kernbichler, Monticello, Nemov, Nührenberg and Reiman2003) for 16 radial points. A maximum value of $\epsilon _{\mathrm {eff}}=1\,\%$![]() is found, as shown in figure 18. The values of the effective ripple are similar to those of the standard configuration of W7-X, with the important distinction that this configuration consists entirely of elliptical cross-sections and no boundary optimization was required. Half-helicity configurations seem to provide the high rotational transform benefits from $m=1$
is found, as shown in figure 18. The values of the effective ripple are similar to those of the standard configuration of W7-X, with the important distinction that this configuration consists entirely of elliptical cross-sections and no boundary optimization was required. Half-helicity configurations seem to provide the high rotational transform benefits from $m=1$![]() configurations while preserving the low values of neoclassical transport found in $m=0$
configurations while preserving the low values of neoclassical transport found in $m=0$![]() equilibria. In the next section we show that we can take advantage of this property to construct $N>3$
equilibria. In the next section we show that we can take advantage of this property to construct $N>3$![]() equilibria with low effective ripple.
equilibria with low effective ripple.
6. The half-helicity space
Now that we have adjusted the near-axis method to deal with the possibility of half-helicity axes, we proceed to identify in which region of the space of solutions we can find such configurations. Let us analyse the space of five-field-period configurations using the same procedure as that in § 3.
Once again, we hold all parameters fixed, apart from those of the magnetic axis, and we parametrize the axis in cylindrical coordinates as
The aspect ratio is chosen as $A=20$![]() , the function $\alpha (\varphi )$
, the function $\alpha (\varphi )$![]() is described by (2.7) with $k=2$
is described by (2.7) with $k=2$![]() , the magnetic field on axis is $B_0 = 1+0.15\cos (\varphi )$
, the magnetic field on axis is $B_0 = 1+0.15\cos (\varphi )$![]() and $d = 0.73 \kappa ^s$
and $d = 0.73 \kappa ^s$![]() . Each colour-coded square in figure 11 is an integer-helicity axis configuration, with values of $z_s(1)$
. Each colour-coded square in figure 11 is an integer-helicity axis configuration, with values of $z_s(1)$![]() ranging from 0 to 0.18 and $z_s(2)$
ranging from 0 to 0.18 and $z_s(2)$![]() from $-$
from $-$![]() 0.425 to 0.425, constructed using the near-axis method described in § 2.
0.425 to 0.425, constructed using the near-axis method described in § 2.

Figure 11. Space of five-field-period near-axis configurations. Squares correspond to integer-helicity values ($m=0,1$![]() ) and circles to half-helicity ($m=1/2$
) and circles to half-helicity ($m=1/2$![]() ). Colours indicate the maximum effective ripple. An example of each type of helicity is shown on the right. Note that the half-helicity configurations attain values of ${\epsilon _{\mathrm {eff}}}{}$
). Colours indicate the maximum effective ripple. An example of each type of helicity is shown on the right. Note that the half-helicity configurations attain values of ${\epsilon _{\mathrm {eff}}}{}$![]() similar to those of integer configurations but have higher values of rotational transform.
similar to those of integer configurations but have higher values of rotational transform.
We also include half-helicity axes for which $R_c(3)$![]() and $z_s(3)$
and $z_s(3)$![]() in expression (4.8) are zero. Thirty-seven values of $z_s(1)$
in expression (4.8) are zero. Thirty-seven values of $z_s(1)$![]() are considered, ranging from 0 to 0.18. In order to fulfil the half-helicity constraints on the axis, $z_s(2)$
are considered, ranging from 0 to 0.18. In order to fulfil the half-helicity constraints on the axis, $z_s(2)$![]() is calculated following expression (4.8):
is calculated following expression (4.8):
The configurations for these axes are constructed as in the previous section: the only difference from the integer-helicity cases is the need to set $m=1/2$![]() when calculating the function $\alpha (\varphi )$
when calculating the function $\alpha (\varphi )$![]() . All other initial parameters are as described earlier in this section. Given how $z_s(1)$
. All other initial parameters are as described earlier in this section. Given how $z_s(1)$![]() depends on the chosen values for $z_s(2)$
depends on the chosen values for $z_s(2)$![]() when restricting ourselves to two parameter curves, the half-helicity space has one dimension fewer than the equivalent integer-helicity space. This is always the case, independently of the number of Fourier coefficients included in the axis representation.
when restricting ourselves to two parameter curves, the half-helicity space has one dimension fewer than the equivalent integer-helicity space. This is always the case, independently of the number of Fourier coefficients included in the axis representation.
In figure 11, the circles correspond to the half-helicity configurations and are distributed on the line where the conditions for second-order zeros of curvature at the maxima of $B_0$![]() are fulfilled. The line in the upper quadrant is for those axes in which $\kappa$
are fulfilled. The line in the upper quadrant is for those axes in which $\kappa$![]() is zero at second order at the minima of $B_0$
is zero at second order at the minima of $B_0$![]() . These are not consistent with near-axis QI equilibria; hence the lack of configurations in said region.
. These are not consistent with near-axis QI equilibria; hence the lack of configurations in said region.
A configuration from the zero-helicity section is shown above a half-helicity configuration in figure 11. Both are the configurations with lowest ${\epsilon _{\mathrm {eff}}}{}$![]() in the boundary, in each space. We can see that both have similar boundary effective ripple values (1.99 % for $m=0$
in the boundary, in each space. We can see that both have similar boundary effective ripple values (1.99 % for $m=0$![]() and 2 % for $m=1/2$
and 2 % for $m=1/2$![]() ) but the rotational transform is substantially larger for the half-helicity case ($\iotaslash _{m=0}=0.23$
) but the rotational transform is substantially larger for the half-helicity case ($\iotaslash _{m=0}=0.23$![]() and $\iotaslash _{m=1/2}=0.85$
and $\iotaslash _{m=1/2}=0.85$![]() ). This behaviour is consistently observed between all configurations in this space. The half-helicity space, apart from its lower dimensionality, also has higher values of rotational transform, closer to the per-field-period values encountered in traditional optimized stellarators. Higher values of rotational transform are desirable as they are related to improved confinement (Ascasíbar et al. Reference Ascasíbar, López-Bruna, Castejon, Vargas, Tribaldos, Maassberg, Beidler, Brakel, Dinklage and Geiger2008) and given the dependence of ideal MHD $\beta$
). This behaviour is consistently observed between all configurations in this space. The half-helicity space, apart from its lower dimensionality, also has higher values of rotational transform, closer to the per-field-period values encountered in traditional optimized stellarators. Higher values of rotational transform are desirable as they are related to improved confinement (Ascasíbar et al. Reference Ascasíbar, López-Bruna, Castejon, Vargas, Tribaldos, Maassberg, Beidler, Brakel, Dinklage and Geiger2008) and given the dependence of ideal MHD $\beta$![]() -limit on $\iotaslash$
-limit on $\iotaslash$![]() (Miyamoto Reference Miyamoto2005; Loizu et al. Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017).
(Miyamoto Reference Miyamoto2005; Loizu et al. Reference Loizu, Hudson, Nührenberg, Geiger and Helander2017).
7. Five-field-period configuration
Up until now it has proven difficult to find configurations with integer helicity, high numbers of field periods and reasonably low aspect ratio, which are accurate to first order, using VMEC as described previously. This is true even when attempting to optimize within the space of near-axis solutions. We now show that this is not the case when searching in the lower-dimensional space of half-helicity magnetic axes in the NAE.
A magnetic axis shape is chosen by varying the Fourier coefficients $R_c(3), z_s(2)$![]() and $z_s(3)$
and $z_s(3)$![]() of expression (4.7) and imposing the half-helicity conditions in (4.8). An axis is selected such that low values of effective ripple are achieved in the boundary. The one used for the construction of the following example is described by
of expression (4.7) and imposing the half-helicity conditions in (4.8). An axis is selected such that low values of effective ripple are achieved in the boundary. The one used for the construction of the following example is described by
The curvature and torsion per field period are shown in figure 12. For this high number of field periods, the magnetic field on axis and the function $d(\varphi )$![]() need to be carefully chosen to reduce $\epsilon _{\mathrm {eff}}$
need to be carefully chosen to reduce $\epsilon _{\mathrm {eff}}$![]() to acceptable levels. These quantities are parametrized as
to acceptable levels. These quantities are parametrized as
Adding more parameters to these expressions allows for a finer profile control. These parameters are varied for a set axis shape until a desired configuration is found. For this example $d_{\kappa }=0.28$![]() , $d_{\kappa c}=-0.065$
, $d_{\kappa c}=-0.065$![]() , $d_{\kappa s}=0.04$
, $d_{\kappa s}=0.04$![]() , $B0_1 = 0.12$
, $B0_1 = 0.12$![]() and $B0_2 = -0.002$
and $B0_2 = -0.002$![]() . The resulting shapes of $B_0(\varphi )$
. The resulting shapes of $B_0(\varphi )$![]() and $\bar {d}(\varphi )$
and $\bar {d}(\varphi )$![]() are shown in figure 13. Here we can observe a non-analytic behaviour present at $\varphi ={\rm \pi} /N$
are shown in figure 13. Here we can observe a non-analytic behaviour present at $\varphi ={\rm \pi} /N$![]() . This arises due to the sine term in expression (7.4) and can be set to zero but including it resulted in lower values of $\epsilon _{\mathrm {eff}}$
. This arises due to the sine term in expression (7.4) and can be set to zero but including it resulted in lower values of $\epsilon _{\mathrm {eff}}$![]() , and, most importantly, it does not result in any sharp behaviour on the plasma boundary. As in the previous section, the function $\alpha$
, and, most importantly, it does not result in any sharp behaviour on the plasma boundary. As in the previous section, the function $\alpha$![]() is defined through (2.7) with $k=2$
is defined through (2.7) with $k=2$![]() . Following the NAE formalism, we construct a solution at a set distance from the axis, in this case $r=1/12$
. Following the NAE formalism, we construct a solution at a set distance from the axis, in this case $r=1/12$![]() corresponding to an aspect ratio $A=12$
corresponding to an aspect ratio $A=12$![]() . However, using the method of § 4.1 of Landreman et al. (Reference Landreman, Sengupta and Plunk2019) was not enough to obtain equilibria with good confinement; instead the method of § 4.2 of the same publication was used. This method, albeit more complicated, results in boundary shapes identical at first order to the boundary in the $X$
. However, using the method of § 4.1 of Landreman et al. (Reference Landreman, Sengupta and Plunk2019) was not enough to obtain equilibria with good confinement; instead the method of § 4.2 of the same publication was used. This method, albeit more complicated, results in boundary shapes identical at first order to the boundary in the $X$![]() –$Y$
–$Y$![]() space, with the caveat that cross-sections in the $R$
space, with the caveat that cross-sections in the $R$![]() –$z$
–$z$![]() plane are no longer elliptical, as can be seen in figure 14. Having a boundary defined by elliptical cross-sections requires the use of less poloidal modes when using equilibrium codes like VMEC and might be useful for plasma boundary optimization, where initial points with low modes are preferred, although not necessary (Landreman Reference Landreman2022).
plane are no longer elliptical, as can be seen in figure 14. Having a boundary defined by elliptical cross-sections requires the use of less poloidal modes when using equilibrium codes like VMEC and might be useful for plasma boundary optimization, where initial points with low modes are preferred, although not necessary (Landreman Reference Landreman2022).

Figure 13. (a) Profiles of $\bar {e}$![]() for the two five-field-period configurations presented. The dotted line correspondsto the configuration with parameter $d(\varphi )$
for the two five-field-period configurations presented. The dotted line correspondsto the configuration with parameter $d(\varphi )$![]() optimized for low elongation. (b) Magnetic field on axis $B_0(\varphi )$
optimized for low elongation. (b) Magnetic field on axis $B_0(\varphi )$![]() used for the construction of these configurations.
used for the construction of these configurations.

Figure 15. Intensity of the magnetic field on the boundary of the five-field-period configuration. (a) Side view and (b) top view.
The intensity of the magnetic field on the boundary, as obtained from VMEC, is shown in figure 15. Despite the contours of $|B|$![]() looking far from the expected behaviour for a QI field, this configuration has good neoclassical confinement properties, as is evident from its effective ripple profile in figure 18. With ${\epsilon _{\mathrm {eff}}}{}$
looking far from the expected behaviour for a QI field, this configuration has good neoclassical confinement properties, as is evident from its effective ripple profile in figure 18. With ${\epsilon _{\mathrm {eff}}}{}$![]() $\approx 1.3\,\%$
$\approx 1.3\,\%$![]() it is comparable to that of W7-X and QIPC without the need of performing a boundary optimization. As is typical for near-axis configurations, the contours of $|B|$
it is comparable to that of W7-X and QIPC without the need of performing a boundary optimization. As is typical for near-axis configurations, the contours of $|B|$![]() resemble more straight poloidally closed contours the closer we look to the axis, as seen in figure 16.
resemble more straight poloidally closed contours the closer we look to the axis, as seen in figure 16.

Figure 16. Contours of magnetic field intensity for the configuration in § 7 at $s=0.1$![]() (a), $s=0.5$
(a), $s=0.5$![]() (b) and $s=1$
(b) and $s=1$![]() (c). The poloidally closed contours of $B$
(c). The poloidally closed contours of $B$![]() , characteristic of QI configurations, degrade with distance from the axis.
, characteristic of QI configurations, degrade with distance from the axis.
The elongation of the plasma boundary cross-sections in the cylindrical angle $\phi$![]() is shown in figure 14, where a maximum value of $e=5.05$
is shown in figure 14, where a maximum value of $e=5.05$![]() is found. We can observe a clear difference in the elongation profile of this configuration and that of the two-field-period example shown in figure 7. The rotational transform radial profile for this configuration is shown in figure 17, where is clear the per-field-period rotational transform value achieved is close to those in existing optimized stellarators.
is found. We can observe a clear difference in the elongation profile of this configuration and that of the two-field-period example shown in figure 7. The rotational transform radial profile for this configuration is shown in figure 17, where is clear the per-field-period rotational transform value achieved is close to those in existing optimized stellarators.

Figure 17. Rotational transform profile for the five-field-period configuration of § 7.
7.1. Optimizing $d$ for low elongation
for low elongation
The choice of the function $d(\varphi )$![]() plays an important role in the resulting elongation of the plasma boundary and needs to be chosen carefully, as most values will result in impractically large elongations. This function can be tuned to obtain a desired elongation profile, although the dependence on this and other quantities is not straightforward, as is clear from equation (5.1) of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022):Footnote 3
plays an important role in the resulting elongation of the plasma boundary and needs to be chosen carefully, as most values will result in impractically large elongations. This function can be tuned to obtain a desired elongation profile, although the dependence on this and other quantities is not straightforward, as is clear from equation (5.1) of Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022):Footnote 3

For this reason, in the following configuration, $d(\varphi )$![]() is chosen through an optimization procedure to minimize elongation. All other near-axis parameters are kept the same as in the previous example. The function $d$
is chosen through an optimization procedure to minimize elongation. All other near-axis parameters are kept the same as in the previous example. The function $d$![]() is parametrized as
is parametrized as

and the coefficients $d_{\kappa c}(i)$![]() are optimized using an off-the-shelf optimization methodFootnote 4 to reduce the elongation variation, i.e. the difference between the maximum and minimum elongation, both outputs of the NAE construction. For this configuration the values resulting in the elongation shown with a dotted line in figure 14 are
are optimized using an off-the-shelf optimization methodFootnote 4 to reduce the elongation variation, i.e. the difference between the maximum and minimum elongation, both outputs of the NAE construction. For this configuration the values resulting in the elongation shown with a dotted line in figure 14 are
corresponding to $\bar {e}(\varphi )$![]() shown in figure 13. We can see that the variation in the elongation profile is greatly reduced compared with the previous configuration, which is also evident by looking at the toroidal cross-sections of the plasma boundary shown in figure 19, and comparing them with the previous configuration as done in figure 20. But even using four Fourier modes in the representation of $d(\varphi )$
shown in figure 13. We can see that the variation in the elongation profile is greatly reduced compared with the previous configuration, which is also evident by looking at the toroidal cross-sections of the plasma boundary shown in figure 19, and comparing them with the previous configuration as done in figure 20. But even using four Fourier modes in the representation of $d(\varphi )$![]() is not enough to obtain a constant elongation profile, which is a particularly attractive case, allowed by the NAE QI theory, due to its especially smooth boundary behaviour. This fact, together with the complicated dependence of elongation, and the parameters required for the equilibrium construction (see (7.6)), as well as the non-analyticity of $\bar {d}(\varphi )$
is not enough to obtain a constant elongation profile, which is a particularly attractive case, allowed by the NAE QI theory, due to its especially smooth boundary behaviour. This fact, together with the complicated dependence of elongation, and the parameters required for the equilibrium construction (see (7.6)), as well as the non-analyticity of $\bar {d}(\varphi )$![]() necessary to achieve good confinement in the example in § 7 are clear indications of the unsuitability of $d(\varphi )$
necessary to achieve good confinement in the example in § 7 are clear indications of the unsuitability of $d(\varphi )$![]() as a natural input parameter for the NAE. A possible solution to this problem is specifying the elongation function as an input parameter instead. This will be described in a future publication.
as a natural input parameter for the NAE. A possible solution to this problem is specifying the elongation function as an input parameter instead. This will be described in a future publication.

Figure 18. Effective helical ripple ${\epsilon _{\mathrm {eff}}}{}$![]() for the three configurations shown in this work (solid lines) and two QI optimized configurations: W7-X (dotted line) and QIPC (dashed line).
for the three configurations shown in this work (solid lines) and two QI optimized configurations: W7-X (dotted line) and QIPC (dashed line).

Figure 19. (a) Cross-sections of the configuration shown in figure 21. (b) Rotational transform profile for the same configuration.

Figure 20. Cross-section comparisons between the two five-field-period configurations shown in § 7 at different toroidal locations. Dotted lines correspond to the configuration optimized for constant elongation.
The rotational transform profile is shown in figure 19. It crosses the value $\iotaslash =1$![]() , which might result in the presence of magnetic islands degrading the nested flux surfaces necessary for confinement. No effort has been made in this work to avoid such regions and further optimization of this configuration with specific targets to limit $\iotaslash$
, which might result in the presence of magnetic islands degrading the nested flux surfaces necessary for confinement. No effort has been made in this work to avoid such regions and further optimization of this configuration with specific targets to limit $\iotaslash$![]() can be applied if necessary.
can be applied if necessary.
The intensity of the magnetic field on the boundary ($A=12$![]() ) for the configuration constructed in this section is shown in figure 21. We can see that the contours at maximum field do not close as expected but nonetheless $\epsilon _{\mathrm {eff}}$
) for the configuration constructed in this section is shown in figure 21. We can see that the contours at maximum field do not close as expected but nonetheless $\epsilon _{\mathrm {eff}}$![]() remains under $1\,\%$
remains under $1\,\%$![]() for half-flux and is comparable to that of QIPC in the remaining region as shown in figure 18. As expected, a reduction in elongation results in worse QI quality as discussed in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).
for half-flux and is comparable to that of QIPC in the remaining region as shown in figure 18. As expected, a reduction in elongation results in worse QI quality as discussed in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022).

Figure 21. Magnetic field intensity on the boundary for the five-field-period low-elongation configuration described in § 7.1. (a) Side view and (b) top view.
8. Conclusions
Using the NAE method, at first order, we have analysed the impact the magnetic axis helicity has on the quality of the construction of QI stellarator-symmetric configurations.
The difficulties encountered when performing stellarator boundary optimization have often been associated with the complexity of the solution space. As a first step to understanding the landscape of solutions, we generated a multitude of configurations with identical near-axis parameters, differing only in their axis shape. This was parametrized by two terms in a Fourier representation of the axis. We show how the helicity of the magnetic axis divides the space of QI near-axis configurations with clear divisions between the considered helicities, $m=0$![]() and $m=1$
and $m=1$![]() . The effective ripple was calculated for each of the constructed configurations and a region of poor-quality configurations (extremely elongated or effective ripple larger than 1 %) was observed in the helicity transition region. Notably, consistently lower values of effective ripple were observed for the zero-helicity region compared with the helicity one, with this behaviour being present at different number of field periods. However, given the relation between helicity and integrated torsion, the configurations in the $m=0$
. The effective ripple was calculated for each of the constructed configurations and a region of poor-quality configurations (extremely elongated or effective ripple larger than 1 %) was observed in the helicity transition region. Notably, consistently lower values of effective ripple were observed for the zero-helicity region compared with the helicity one, with this behaviour being present at different number of field periods. However, given the relation between helicity and integrated torsion, the configurations in the $m=0$![]() region have low values of rotational transform. The presence of a sharp division between helicity regions would make it challenging for an optimizer to find solutions outside of its starting region.
region have low values of rotational transform. The presence of a sharp division between helicity regions would make it challenging for an optimizer to find solutions outside of its starting region.
Stellarators such as QIPC (Subbotin et al. Reference Subbotin, Mikhailov, Shafranov, Isaev, Nührenberg, Nührenberg, Zille, Nemov, Kasilov and Kalyuzhnyj2006) that were optimized by conventional means rather than through the NAE sometimes possess a half-helicity axis, so that the normal vector performs exactly half a rotation around the axis in every field period. The conditions on the coefficients of a Fourier series necessary for achieving this behaviour were calculated and correspond to the transition between integer-helicity regions. We show that half-helicity axes are compatible with the near-axis formalism when modifying the $\alpha (\varphi )$![]() function accordingly. We present a two-field-period configuration constructed around one such axis. At an aspect ratio $A=10$
function accordingly. We present a two-field-period configuration constructed around one such axis. At an aspect ratio $A=10$![]() the maximum ${\epsilon _{\mathrm {eff}}}{}$
the maximum ${\epsilon _{\mathrm {eff}}}{}$![]() is 1 %, $\iotaslash =0.35$
is 1 %, $\iotaslash =0.35$![]() –$0.37$
–$0.37$![]() and the maximum elongation remains under $e=5.5$
and the maximum elongation remains under $e=5.5$![]() .
.
The case of five field periods was investigated, locating the half-helicity configurations within the solution space. We note that, when using a set number of Fourier axis modes, the half-helicity space has one fewer dimension compared with the integer-helicity space. This is especially relevant when a low number of Fourier modes are being used as is in this work.
In this way, configurations with $N=5$![]() were found with an aspect ratio $A=12$
were found with an aspect ratio $A=12$![]() and lower effective ripple (${\epsilon _{\mathrm {eff}}}{}$
and lower effective ripple (${\epsilon _{\mathrm {eff}}}{}$![]() $\approx 1.3\,\%$
$\approx 1.3\,\%$![]() ) than previously achieved for near-axis QI configurations with this high number of field periods. We also demonstrate the utility of $d(\varphi )$
) than previously achieved for near-axis QI configurations with this high number of field periods. We also demonstrate the utility of $d(\varphi )$![]() in managing elongation, by showing a configuration with a low toroidal variation of this quantity. It is noted that this control over elongation, due to the freedom in $d$
in managing elongation, by showing a configuration with a low toroidal variation of this quantity. It is noted that this control over elongation, due to the freedom in $d$![]() , is not possible for quasi-symmetric configurations, and it is planned to investigate this further in a future publication.
, is not possible for quasi-symmetric configurations, and it is planned to investigate this further in a future publication.
The use of half-helicity axes makes it possible to construct QI stellarators with characteristics similar to those of existing traditionally optimized QI devices, and opens the door to exploring the space of solutions in a systematic way by using near-axis configurations in the high-$N$![]() region of space. Using near-axis QI solutions as initial points for boundary optimization will allow the expansion of the QI library of suitable reactor configurations. The use of optimization within the near-axis space is being currently explored to identify particularly good initial points for further optimization.
region of space. Using near-axis QI solutions as initial points for boundary optimization will allow the expansion of the QI library of suitable reactor configurations. The use of optimization within the near-axis space is being currently explored to identify particularly good initial points for further optimization.
Acknowledgements
The authors would like to thank M. Landreman for providing the numerical code, described in Plunk et al. (Reference Plunk, Landreman and Helander2019), which was adapted for the present study. We are grateful to C. Nührenberg for providing the QIPC configuration and for illuminating clarifications, to M. Drevlak for providing the code used for calculating the effective ripple, to E. Rodríguez for pointing out the analytical conditions necessary for the helicity transition and for fruitful discussions and to P. Helander for guidance while preparing the manuscript.
Editor P. Catto thanks the referees for their advice in evaluating this article.
Funding
This work was partly supported by a grant from the Simons Foundation (560651, K.C.M.).
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data that support the findings of this study are available from the corresponding author, K.C.M., upon reasonable request.
Appendix A. Conditions for zeros of curvature
Given the need to have points of zero curvature on the magnetic axis, it is important to be able to control this behaviour at different orders. We reproduce here the relevant parts of Appendix B in Camacho Mata et al. (Reference Camacho Mata, Plunk and Jorge2022) for our discussion.
We use the Fourier axis representation (4.1) and (4.2), and we employ a Taylor expansion to describe the axis locally, around points of stellarator symmetry (which coincide with extrema of $B_0$![]() ):
):
where $R_n$![]() and $Z_n$
and $Z_n$![]() denote the $n$
denote the $n$![]() th derivatives with respect to $\varphi$
th derivatives with respect to $\varphi$![]() . We can also see from the curvature and torsion expressions for a general parametrization,
. We can also see from the curvature and torsion expressions for a general parametrization,
that we need to calculate up to third derivatives of the axis position function $x(\phi )$![]() . These derivatives can be easily calculated by noting $d\hat {\boldsymbol R}/d\phi = \hat {\boldsymbol \phi }$
. These derivatives can be easily calculated by noting $d\hat {\boldsymbol R}/d\phi = \hat {\boldsymbol \phi }$![]() and $d\hat {\boldsymbol \phi }/d\phi = -\hat {\boldsymbol R}$
and $d\hat {\boldsymbol \phi }/d\phi = -\hat {\boldsymbol R}$![]() . Further substituting the expansions for $R$
. Further substituting the expansions for $R$![]() and $z$
and $z$![]() , (A1)–(A2), the contributions to each derivative can be collected by their order in $\phi$
, (A1)–(A2), the contributions to each derivative can be collected by their order in $\phi$![]() , the following properties can be confirmed:
, the following properties can be confirmed:
where the subscript $m$![]() denotes the ($m$
denotes the ($m$![]() +1)th order in $\phi$
+1)th order in $\phi$![]() .
.
Now we can proceed to find the necessary conditions for having zeros in curvature at a given order $(m+1)$![]() . We will classify the zeros in curvature by the order of the first non-zero term in the power series, for example
. We will classify the zeros in curvature by the order of the first non-zero term in the power series, for example
Assuming that ${\boldsymbol x}^\prime$![]() is itself non-zero, the conditions on zeros in curvature are found by requiring
is itself non-zero, the conditions on zeros in curvature are found by requiring
at each order in $\phi$![]() . At first order ($m=0$
. At first order ($m=0$![]() ), ${\boldsymbol x}^{\prime \prime }$
), ${\boldsymbol x}^{\prime \prime }$![]() has its only non-zero component in the $\hat {\boldsymbol R}$
has its only non-zero component in the $\hat {\boldsymbol R}$![]() direction, and the condition ${\boldsymbol x}^\prime \times {\boldsymbol x}^{\prime \prime } = 0$
direction, and the condition ${\boldsymbol x}^\prime \times {\boldsymbol x}^{\prime \prime } = 0$![]() is satisfied by ${\boldsymbol x}^{\prime \prime }\boldsymbol {\cdot }\hat {\boldsymbol R} = 0$
is satisfied by ${\boldsymbol x}^{\prime \prime }\boldsymbol {\cdot }\hat {\boldsymbol R} = 0$![]() , which results in the condition
, which results in the condition
The curvature can be made zero to higher order by considering higher-order contributions to ${\boldsymbol x}^{\prime \prime }$![]() . At odd orders, these are contained in the $\hat {\boldsymbol { \phi }}$
. At odd orders, these are contained in the $\hat {\boldsymbol { \phi }}$![]() –$\hat {\boldsymbol z}$
–$\hat {\boldsymbol z}$![]() plane and must be made parallel to the zeroth-order contribution from ${\boldsymbol x}^\prime$
plane and must be made parallel to the zeroth-order contribution from ${\boldsymbol x}^\prime$![]() , while at even orders, the even-order contribution to ${\boldsymbol x}^{\prime \prime }$
, while at even orders, the even-order contribution to ${\boldsymbol x}^{\prime \prime }$![]() must simply be zero. Thus, conditions at arbitrary order can be obtained, and a few are listed in table 1.
must simply be zero. Thus, conditions at arbitrary order can be obtained, and a few are listed in table 1.
Table 1. Conditions for zero curvature.

The tabulated constraints on the derivatives of the axis components can be applied to a truncated Fourier representation. Equations (4.7) are simply substituted into the constraint equations with $\phi$![]() set to a location of stellarator symmetry (for instance at $\phi = 0, {\rm \pi}/N$
set to a location of stellarator symmetry (for instance at $\phi = 0, {\rm \pi}/N$![]() in the first period). This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra.
in the first period). This results in a set of linear conditions on the Fourier coefficients that can be solved numerically, or by computer algebra.
As a simple example let us consider the family of 2-mode curves:
Enforcing the conditions for first-order zeros of curvature ($R_0-R_2 = 0$![]() ) at extrema of $B_0$
) at extrema of $B_0$![]() , $\phi = 0$
, $\phi = 0$![]() and $\phi = {\rm \pi}/N$
and $\phi = {\rm \pi}/N$![]() gives
gives
Having second-order zeros of $\kappa$![]() requires imposing conditions on the $z$
requires imposing conditions on the $z$![]() coefficients. At $\phi =0$
coefficients. At $\phi =0$![]() this results in
this results in
and when imposing it at the minima of $B_0$![]()