Published online by Cambridge University Press: 08 February 2022
The linear and nonlinear evolutions of the tearing instability in a collisionless plasma with a strong guide field are analysed on the basis of a two-field Hamiltonian gyrofluid model. The model is valid for a low ion temperature and a finite $\beta _e$ . The finite $\beta _e$
. The finite $\beta _e$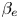 effect implies a magnetic perturbation along the guide field direction, and electron finite Larmor radius effects. A Hamiltonian derivation of the model is presented. A new dispersion relation of the tearing instability is derived for the case $\beta _e=0$
effect implies a magnetic perturbation along the guide field direction, and electron finite Larmor radius effects. A Hamiltonian derivation of the model is presented. A new dispersion relation of the tearing instability is derived for the case $\beta _e=0$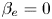 and tested against numerical simulations. For $\beta _e \ll 1$
and tested against numerical simulations. For $\beta _e \ll 1$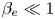 the equilibrium electron temperature is seen to enhance the linear growth rate, whereas we observe a stabilizing role when electron finite Larmor radius effects become more relevant. In the nonlinear phase, stall phases and faster than exponential phases are observed, similarly to what occurs in the presence of ion finite Larmor radius effects. Energy transfers are analysed and the conservation laws associated with the Casimir invariants of the model are also discussed. Numerical simulations seem to indicate that finite $\beta _e$
the equilibrium electron temperature is seen to enhance the linear growth rate, whereas we observe a stabilizing role when electron finite Larmor radius effects become more relevant. In the nonlinear phase, stall phases and faster than exponential phases are observed, similarly to what occurs in the presence of ion finite Larmor radius effects. Energy transfers are analysed and the conservation laws associated with the Casimir invariants of the model are also discussed. Numerical simulations seem to indicate that finite $\beta _e$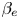 effects do not produce qualitative modifications in the structures of the Lagrangian invariants associated with Casimirs of the model.
effects do not produce qualitative modifications in the structures of the Lagrangian invariants associated with Casimirs of the model.