Article contents
Fast magneto-acoustic wave turbulence and the Iroshnikov–Kraichnan spectrum
Published online by Cambridge University Press: 31 March 2023
Abstract
An analytical theory of wave turbulence is developed for pure compressible magnetohydrodynamics in the small $\beta$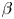 limit. In contrast to previous works where the multiple scale method was not mentioned and slow magneto-acoustic waves were included, we present here a theory for fast magneto-acoustic waves for which only an asymptotic closure is possible in three dimensions. We introduce the compressible Elsässer fields (canonical variables) and show their linear relationship with the mass density and the compressible velocity. The kinetic equations of wave turbulence for three-wave interactions are obtained and the detailed conservation is shown for the two invariants, energy and momentum (cross-helicity). An exact stationary solution (Kolmogorov-Zakharov spectrum) exists only for the energy. We find a $k^{-3/2}$
limit. In contrast to previous works where the multiple scale method was not mentioned and slow magneto-acoustic waves were included, we present here a theory for fast magneto-acoustic waves for which only an asymptotic closure is possible in three dimensions. We introduce the compressible Elsässer fields (canonical variables) and show their linear relationship with the mass density and the compressible velocity. The kinetic equations of wave turbulence for three-wave interactions are obtained and the detailed conservation is shown for the two invariants, energy and momentum (cross-helicity). An exact stationary solution (Kolmogorov-Zakharov spectrum) exists only for the energy. We find a $k^{-3/2}$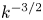 energy spectrum compatible with the Iroshnikov–Kraichnan (IK) phenomenological prediction; this leads to a mass density spectrum with the same scaling. Despite the presence of a relatively strong uniform magnetic field, this turbulence is characterized by an energy spectrum with a power index that is independent of the angular direction; its amplitude, however, shows an angular dependence. We prove the existence of the IK solution using the locality condition, show that the energy flux is positive and hence the cascade direct and find the Kolmogorov constant. This theory offers a plausible explanation for recent observations in the solar wind at small $\beta$
energy spectrum compatible with the Iroshnikov–Kraichnan (IK) phenomenological prediction; this leads to a mass density spectrum with the same scaling. Despite the presence of a relatively strong uniform magnetic field, this turbulence is characterized by an energy spectrum with a power index that is independent of the angular direction; its amplitude, however, shows an angular dependence. We prove the existence of the IK solution using the locality condition, show that the energy flux is positive and hence the cascade direct and find the Kolmogorov constant. This theory offers a plausible explanation for recent observations in the solar wind at small $\beta$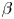 where isotropic spectra with a $-3/2$
where isotropic spectra with a $-3/2$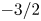 power-law index are found and associated with fast magneto-acoustic waves. This theory may also be used to explain the IK spectrum often observed near the Sun. Besides, it provides a rigorous theoretical basis for the well-known phenomenological IK spectrum, which coincides with the Zakharov–Sagdeev spectrum for acoustic wave turbulence.
power-law index are found and associated with fast magneto-acoustic waves. This theory may also be used to explain the IK spectrum often observed near the Sun. Besides, it provides a rigorous theoretical basis for the well-known phenomenological IK spectrum, which coincides with the Zakharov–Sagdeev spectrum for acoustic wave turbulence.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press
References
- 9
- Cited by



