Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-27T09:06:34.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of shaping on turbulent dynamics in reversed-field pinch simulations

Published online by Cambridge University Press:  29 November 2021

Robert Chahine ,
Kai Schneider Open the ORCID record for Kai Schneider [Opens in a new window]  and
Wouter J.T. Bos Open the ORCID record for Wouter J.T. Bos [Opens in a new window]
Robert Chahine
Affiliation:
Univ Lyon, CNRS, Ecole Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon 1, LMFA, UMR5509, 69340 Ecully, France
Kai Schneider
Affiliation:
Aix-Marseille Université, CNRS, Institut de Mathématiques de Marseille (I2M), UMR 7373, 39 rue Joliot-Curie, 13453 Marseille cedex 13, France
Wouter J.T. Bos*
Affiliation:
Univ Lyon, CNRS, Ecole Centrale de Lyon, INSA Lyon, Univ Claude Bernard Lyon 1, LMFA, UMR5509, 69340 Ecully, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the influence of the shape of the plasma container on the dynamics of the reversed-field pinch (RFP). The geometries we consider are periodic cylinders with elliptical and circular-shaped cross-sections. Numerical simulations of fully nonlinear viscoresistive magnetohydrodynamics are carried out to illustrate how the plasma dynamics is affected by shaping. It is shown that independent of the plasma shape, the quantity $\beta$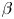, comparing the hydrodynamic pressure to the magnetic pressure, decreases for increasing values of the Lundquist number, but the pressure gradient fluctuations remain roughly constant, when compared to the Lorentz force. Different elliptical shapes of the cross-section of the domain lead to the excitation of different toroidal (or axial) magnetic and dynamic modes. Furthermore, it is found that in a geometry with circular cross-section, a significant local poloidal angular momentum is observed, absent in the geometries with elliptical cross-section. Because the confinement is dominantly determined by plasma movement, and the dynamics of the velocity and magnetic field are modified by the modification of the geometry, shaping can thus affect the performance of RFP devices.

Keywords

MHD and ElectrohydrodynamicsMHD turbulenceplasmas
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 6 , December 2021 , 905870608
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: Rio Tinto Aluminium, Voreppe, France.

References

REFERENCES

Almagri, A., Assadi, S., Dexter, R., Prager, S., Sarff, J. & Sprott, J. 1987 Studies of large, non-circular, reversed field pinch discharges. Nucl. Fusion 27 (11), 1795.CrossRefGoogle Scholar
Biskamp, D. 1993 Nonlinear Magnetohydrodynamics. Cambridge University Press.CrossRefGoogle Scholar
Bonfiglio, D., Cappello, S. & Escande, D. 2016. Impact of a uniform plasma resistivity in MHD modelling of helical solutions for the reversed field pinch dynamo. arXiv:1603.03563.Google Scholar
Bonfiglio, D., Veranda, M., Cappello, S., Escande, D. & Chacón, L. 2013 Experimental-like helical self-organization in reversed-field pinch modeling. Phys. Rev. Lett. 111 (8), 085002.CrossRefGoogle ScholarPubMed
Bonofiglo, P.J., Anderson, J.K., Gobbin, M., Spong, D.A., Boguski, J., Parke, E., Kim, J. & Egedal, J. 2019 Fast ion transport in the quasi-single helical reversed-field pinch. Phys. Plasmas 26, 022502.CrossRefGoogle Scholar
Bos, W.J.T., Neffaa, S. & Schneider, K. 2008 Rapid generation of angular momentum in bounded magnetized plasma. Phys. Rev. Lett. 101 (23), 235003.CrossRefGoogle ScholarPubMed
Bos, W.J.T., Neffaa, S. & Schneider, K. 2010 Self-organization and symmetry-breaking in two-dimensional plasma turbulence. Phys. Plasmas 17 (9), 092302.CrossRefGoogle Scholar
Canuto, C., Hussaini, M., Quarteroni, A. & Zang, T. 1987 Spectral Methods in Fluid Dynamics. Springer.Google Scholar
Cappello, S. & Biskamp, D. 1996 Reconnection processes and scaling laws in reversed field pinch magnetohydrodynamics. Nucl. Fusion 36, 571.CrossRefGoogle Scholar
Cappello, S. & Escande, D.F. 2000 Bifurcation in viscoresistive MHD: the Hartmann number and the reversed field pinch. Phys. Rev. Lett. 85 (18), 3838.CrossRefGoogle ScholarPubMed
Chahine, R. & Bos, W.J.T. 2018 On the role and value of $\beta$ in incompressible MHD simulations. Phys. Plasmas 25 (4), 042115.CrossRefGoogle Scholar
Escande, D.F., Martin, P., Ortolani, S., Buffa, A., Franz, P., Marrelli, L., Martines, E., Spizzo, G., Cappello, S., Murari, A., et al. 2000 Quasi-single-helicity reversed-field-pinch plasmas. Phys. Rev. Lett. 85, 1662.CrossRefGoogle ScholarPubMed
Finn, J.M., Nebel, R. & Bathke, C. 1992 Single and multiple helicity ohmic states in reversed-field pinches. Phys. Fluids B 4 (5), 1262–1279.CrossRefGoogle Scholar
Frassinetti, L., Predebon, I., Koguchi, H., Yagi, Y., Hirano, Y., Sakakita, H., Spizzo, G. & White, R. 2006 Improved particle confinement in transition from multiple-helicity to quasi-single-helicity regimes of a reversed-field pinch. Phys. Rev. Lett. 97 (17), 175001.CrossRefGoogle ScholarPubMed
Futatani, S., Morales, J.A. & Bos, W.J.T. 2015 Dynamic equilibria and magnetohydrodynamic instabilities in toroidal plasmas with non-uniform transport coefficients. Phys. Plasmas 22 (5), 052503.CrossRefGoogle Scholar
Futch, A., Craig, D., Hesse, R. & Jacobson, C. 2018 Role of resistivity and viscosity in the excitation of stable $m= 0$ modes during the RFP sawtooth crash. Phys. Plasmas 25 (11), 112506.CrossRefGoogle Scholar
Guo, S., Xu, X., Wang, Z. & Liu, Y. 2013 Does shaping bring an advantage for reversed field pinch plasmas? Nucl. Fusion 53 (11), 113035.CrossRefGoogle Scholar
Keetels, G., Clercx, H. & van Heijst, G. 2008 Spontaneous angular momentum generation of two-dimensional fluid flow in an elliptic geometry. Phys. Rev. E 78 (3), 036301.CrossRefGoogle Scholar
Li, J., Liu, S., Kong, W., Guo, S. & Dong, J. 2019 Effects of trapped electrons and impurity ions on ITG modes in reversed-field pinch plasmas. Europhys. Lett. 127 (4), 45002.CrossRefGoogle Scholar
Lorenzini, R., Martines, E., Piovesan, P., Terranova, D., Zanca, P., Zuin, M., Alfier, A., Bonfiglio, D., Bonomo, F., Canton, A., et al. 2009 Self-organized helical equilibria as a new paradigm for ohmically heated fusion plasmas. Nat. Phys. 5 (8), 570–574.CrossRefGoogle Scholar
Martin, P., Apolloni, L., Puiatti, M., Adamek, J., Agostini, M., Alfier, A., Annibaldi, S.V., Antoni, V., Auriemma, F., Barana, O., et al. 2009 Overview of RFX-mod results. Nucl. Fusion 49 (10), 104019.CrossRefGoogle Scholar
Martin, P., Buffa, A., Cappello, S., D'Angelo, F., Escande, D., Franz, P., Marrelli, L., Martines, E., Ortolani, S., Spizzo, G., et al. 2000 Quasi-single helicity states in the reversed field pinch: beyond the standard paradigm. Phys. Plasmas 7 (5), 1984.CrossRefGoogle Scholar
Martin, P., Marrelli, L., Spizzo, G., Franz, P., Piovesan, P., Predebon, I., Bolzonella, T., Cappello, S., Cravotta, A., Escande, D., et al. 2003 Overview of quasi-single helicity experiments in reversed field pinches. Nucl. Fusion 43 (12), 1855.CrossRefGoogle Scholar
Mizuguchi, N., Sanpei, A., Fujita, S., Oki, K., Himura, H., Masamune, S. & Ichiguchi, K. 2012 Modeling of formation of helical structures in reversed-field pinch. Plasma Fusion Res. 7, 2403117–2403117.CrossRefGoogle Scholar
Momo, B., Isliker, H., Cavazzana, R., Zuin, M., Cordaro, L., Lopez-Bruna, D., Martines, E., Predebon, I., Rea, C., Spolaore, M., et al. 2020 The phenomenology of reconnection events in the reversed field pinch. Nucl. Fusion 60 (5), 056023.CrossRefGoogle Scholar
Morales, J.A., Bos, W.J.T., Schneider, K. & Montgomery, D.C. 2012 Intrinsic rotation of toroidally confined magnetohydrodynamics. Phys. Rev. Lett. 109 (17), 175002.CrossRefGoogle ScholarPubMed
Morales, J.A., Bos, W.J.T., Schneider, K. & Montgomery, D.C. 2014 a On the effect of toroidicity on reversed field pinch dynamics. Plasma Phys. Control. Fusion 56 (9), 095024.CrossRefGoogle Scholar
Morales, J.A., Leroy, M., Bos, W.J.T. & Schneider, K. 2014 b Simulation of confined magnetohydrodynamic flows with Dirichlet boundary conditions using a pseudo-spectral method with volume penalization. J. Comput. Phys. 274, 64–94.CrossRefGoogle Scholar
Oomens, A., Lassing, H. & Meer, A.V. D. 1990 Reversed Field Pinch discharges with elongated minor cross-section. Rijnhuizen Rep. 90-197. FOM-Instituut voor Plasmafysica.Google Scholar
Oueslati, H. & Firpo, M.-C. 2020 Breaking up-down symmetry with magnetic perturbations in tokamak plasmas: increase of axisymmetric steady-state velocities. Phys. Plasmas 27 (10), 102501.CrossRefGoogle Scholar
Paccagnella, R., Bondeson, A. & Lütjens, H. 1991 Ideal toroidal stability beta limits and shaping effect for reversed field pinch configurations. Nucl. Fusion 31 (10), 1899.CrossRefGoogle Scholar
Piovesan, P., Bonfiglio, D., Auriemma, F., Bonomo, F., Carraro, L., Cavazzana, R., De Masi, G., Fassina, A., Franz, P., Gobbin, M., et al. 2013 RFX-mod: a multi-configuration fusion facility for three-dimensional physics studies. Phys. Plasmas 20 (5), 056112.CrossRefGoogle Scholar
Piovesan, P., Bonfiglio, D., Bonomo, F., Cappello, S., Carraro, L., Cavazzana, R., Gobbin, M., Marrelli, L., Martin, P., Martines, E., et al. 2011 Influence of external 3D magnetic fields on helical equilibrium and plasma flow in RFX-mod. Plasma Phys. Control. Fusion 53 (8), 084005.CrossRefGoogle Scholar
Piovesan, P., Zuin, M., Alfier, A., Bonfiglio, D., Bonomo, F., Canton, A., Cappello, S., Carraro, L., Cavazzana, R., Escande, D., et al. 2009 Magnetic order and confinement improvement in high-current regimes of RFX-mod with MHD feedback control. Nucl. Fusion 49 (8), 085036.CrossRefGoogle Scholar
Qu, Z., Dewar, R.L., Ebrahimi, F., Anderson, J.K., Hudson, S.R. & Hole, M.J. 2020 Stepped pressure equilibrium with relaxed flow and applications in reversed-field pinch plasmas. Plasma Phys. Control. Fusion 62 (5), 054002.CrossRefGoogle Scholar
Reiman, A. 1980 Minimum energy state of a toroidal discharge. Phys. Fluids 23.CrossRefGoogle Scholar
Reiman, A. 1981 Taylor relaxation in a torus of arbitrary aspect ratio and cross section. Phys. Fluids 24 (5), 956–963.CrossRefGoogle Scholar
Richardson, A., Finn, J. & Delzanno, G. 2010 Control of ideal and resistive magnetohydrodynamic modes in reversed field pinches with a resistive wall. Phys. Plasmas 17 (11), 112511.CrossRefGoogle Scholar
Sarff, J. 2020 Reversed field pinch research in MST-final technical report. Tech. Rep. No. DOE-UWMADISON-ER54814. The Board of Regents of the University of Wisconsin.CrossRefGoogle Scholar
Shan, X. & Montgomery, D. 1994 Magnetohydrodynamic stabilization through rotation. Phys. Rev. Lett. 73 (12), 1624.CrossRefGoogle ScholarPubMed
Taylor, J. 1974 Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33 (19), 1139.CrossRefGoogle Scholar
Taylor, J.B. 1986 Relaxation and magnetic reconnection in plasmas. Rev. Mod. Phys. 58 (3), 741.CrossRefGoogle Scholar
Terranova, D., Alfier, A., Bonomo, F., Franz, P., Innocente, P. & Pasqualotto, R. 2007 Enhanced confinement and quasi-single-helicity regimes induced by poloidal current drive. Phys. Rev. Lett. 99 (9), 095001.CrossRefGoogle ScholarPubMed
Troyon, F., Gruber, R., Saurenmann, H., Semenzato, S. & Succi, S. 1984 MHD-limits to plasma confinement. Plasma Phys. Control. Fusion 26 (1A), 209.CrossRefGoogle Scholar
Veranda, M., Bonfiglio, D., Cappello, S., Escande, D.F., Auriemma, F., Borgogno, D., Chacón, L., Fassina, A., Franz, P., Gobbin, M., et al. 2017 Magnetohydrodynamics modelling successfully predicts new helical states in reversed-field pinch fusion plasmas. Nucl. Fusion 57 (11), 116029.CrossRefGoogle Scholar
Wesson, J. & Campbell, D.J. 2011 Tokamaks, Vol. 149. Oxford University Press.Google Scholar
Wyman, M., Chapman, B., Ahn, J., Almagri, A., Anderson, J., Bonomo, F., Brower, D., Combs, S.K., Craig, D., Den Hartog, D., et al. 2008 Plasma behaviour at high $\beta$ and high density in the Madison Symmetric Torus RFP. Nucl. Fusion 49 (1), 015003.CrossRefGoogle Scholar