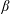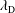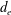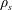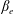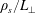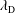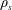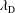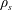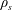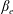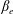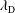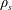1 Introduction
Astrophysical plasmas are often turbulent, with power-law spectra over a wide range of scales. In many situations, a strong background magnetic field
![]() $\boldsymbol{B}_{0}$
can be assumed, and often the plasma is only weakly collisional. A well-studied example of such a system is the solar wind, in which the turbulence is directly measured by spacecraft (Bruno & Carbone Reference Bruno and Carbone2013; Chen Reference Chen2016). The nature of the turbulence depends on how the scale of interest compares to the ion gyroradius
$\boldsymbol{B}_{0}$
can be assumed, and often the plasma is only weakly collisional. A well-studied example of such a system is the solar wind, in which the turbulence is directly measured by spacecraft (Bruno & Carbone Reference Bruno and Carbone2013; Chen Reference Chen2016). The nature of the turbulence depends on how the scale of interest compares to the ion gyroradius
![]() $\unicode[STIX]{x1D70C}_{i}=v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$
, where the ion thermal speed
$\unicode[STIX]{x1D70C}_{i}=v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$
, where the ion thermal speed
![]() $v_{\text{th}i}=\sqrt{2T_{i}/m_{i}}$
and the ion gyrofrequency
$v_{\text{th}i}=\sqrt{2T_{i}/m_{i}}$
and the ion gyrofrequency
![]() $\unicode[STIX]{x1D6FA}_{i}=ZeB_{0}/m_{i}c$
. Regardless of whether the plasma is collisional or collisionless, on length scales much larger than the ion gyroradius,
$\unicode[STIX]{x1D6FA}_{i}=ZeB_{0}/m_{i}c$
. Regardless of whether the plasma is collisional or collisionless, on length scales much larger than the ion gyroradius,
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
, Alfvénically polarised fluctuations obey the reduced magnetohydrodynamic (RMHD) equations (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1973; Strauss Reference Strauss1976; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which describe nonlinearly interacting Alfvén wavepackets (represented by the Elsasser fields
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
, Alfvénically polarised fluctuations obey the reduced magnetohydrodynamic (RMHD) equations (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1973; Strauss Reference Strauss1976; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009), which describe nonlinearly interacting Alfvén wavepackets (represented by the Elsasser fields
![]() $\boldsymbol{z}_{\bot }^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
) propagating up and down the background magnetic field at the Alfvén speed
$\boldsymbol{z}_{\bot }^{\pm }=\boldsymbol{u}\pm \boldsymbol{b}$
) propagating up and down the background magnetic field at the Alfvén speed
![]() $v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}m_{i}n_{i}}$
. At smaller, ‘kinetic’ scales,
$v_{\text{A}}=B_{0}/\sqrt{4\unicode[STIX]{x03C0}m_{i}n_{i}}$
. At smaller, ‘kinetic’ scales,
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$
, the Alfvén waves become dispersive ‘kinetic Alfvén waves’ (as confirmed in the solar wind: see Chen et al.
Reference Chen, Boldyrev, Xia and Perez2013).
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gtrsim 1$
, the Alfvén waves become dispersive ‘kinetic Alfvén waves’ (as confirmed in the solar wind: see Chen et al.
Reference Chen, Boldyrev, Xia and Perez2013).
The structure of strong RMHD turbulence at large scales,
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
, is relatively well understood. First, the fluctuations are ‘critically balanced’ (Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015) – their linear time scale
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\ll 1$
, is relatively well understood. First, the fluctuations are ‘critically balanced’ (Goldreich & Sridhar Reference Goldreich and Sridhar1995, Reference Goldreich and Sridhar1997; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2015) – their linear time scale
![]() $\unicode[STIX]{x1D70F}_{\text{A}}\sim l_{\Vert }/v_{\text{A}}$
and nonlinear time scale
$\unicode[STIX]{x1D70F}_{\text{A}}\sim l_{\Vert }/v_{\text{A}}$
and nonlinear time scale
![]() $\unicode[STIX]{x1D70F}_{\text{nl}}$
are comparable (here
$\unicode[STIX]{x1D70F}_{\text{nl}}$
are comparable (here
![]() $l_{\Vert }$
is the parallel coherence length). This leads to anisotropic fluctuations with
$l_{\Vert }$
is the parallel coherence length). This leads to anisotropic fluctuations with
![]() $l_{\Vert }\gg \unicode[STIX]{x1D706}$
, where
$l_{\Vert }\gg \unicode[STIX]{x1D706}$
, where
![]() $\unicode[STIX]{x1D706}\sim 1/k_{\bot }$
is the perpendicular coherence scale. Second, at least in numerical simulations (Mason, Cattaneo & Boldyrev Reference Mason, Cattaneo and Boldyrev2006; Perez et al.
Reference Perez, Mason, Boldyrev and Cattaneo2012), the fluctuations dynamically ‘align’ so that the vector velocity and magnetic field perturbations point in the same direction up to a small, scale-dependent angle
$\unicode[STIX]{x1D706}\sim 1/k_{\bot }$
is the perpendicular coherence scale. Second, at least in numerical simulations (Mason, Cattaneo & Boldyrev Reference Mason, Cattaneo and Boldyrev2006; Perez et al.
Reference Perez, Mason, Boldyrev and Cattaneo2012), the fluctuations dynamically ‘align’ so that the vector velocity and magnetic field perturbations point in the same direction up to a small, scale-dependent angle
![]() $\unicode[STIX]{x1D703}$
(Boldyrev Reference Boldyrev2006; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017). This causes the fluctuations to become anisotropic within the perpendicular plane, with scale
$\unicode[STIX]{x1D703}$
(Boldyrev Reference Boldyrev2006; Chandran, Schekochihin & Mallet Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017). This causes the fluctuations to become anisotropic within the perpendicular plane, with scale
![]() $\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
in the direction of the vector field perturbations. Together, these two phenomena mean that the turbulent structures are three-dimensionally anisotropic, with
$\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
in the direction of the vector field perturbations. Together, these two phenomena mean that the turbulent structures are three-dimensionally anisotropic, with
![]() $l_{\Vert }\gg \unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
. This anisotropy has been measured both in numerical simulations (Verdini & Grappin Reference Verdini and Grappin2015; Mallet et al.
Reference Mallet, Schekochihin, Chandran, Chen, Horbury, Wicks and Greenan2016) and in the solar wind (Chen et al.
Reference Chen, Mallet, Schekochihin, Horbury, Wicks and Bale2012), and results in the turbulent structures becoming increasingly sheet-like at smaller scales. We review scalings obtained in a simple model of this type of Alfvénic turbulence by Mallet & Schekochihin (Reference Mallet and Schekochihin2017) in § 2. At smaller scales
$l_{\Vert }\gg \unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
. This anisotropy has been measured both in numerical simulations (Verdini & Grappin Reference Verdini and Grappin2015; Mallet et al.
Reference Mallet, Schekochihin, Chandran, Chen, Horbury, Wicks and Greenan2016) and in the solar wind (Chen et al.
Reference Chen, Mallet, Schekochihin, Horbury, Wicks and Bale2012), and results in the turbulent structures becoming increasingly sheet-like at smaller scales. We review scalings obtained in a simple model of this type of Alfvénic turbulence by Mallet & Schekochihin (Reference Mallet and Schekochihin2017) in § 2. At smaller scales
![]() $\unicode[STIX]{x1D706}\lesssim \unicode[STIX]{x1D70C}_{i}$
, the turbulence is also likely to be critically balanced (Cho & Lazarian Reference Cho and Lazarian2004; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Boldyrev & Perez Reference Boldyrev and Perez2012; TenBarge & Howes Reference TenBarge and Howes2012) and has a steeper perpendicular spectral index of approximately
$\unicode[STIX]{x1D706}\lesssim \unicode[STIX]{x1D70C}_{i}$
, the turbulence is also likely to be critically balanced (Cho & Lazarian Reference Cho and Lazarian2004; Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Boldyrev & Perez Reference Boldyrev and Perez2012; TenBarge & Howes Reference TenBarge and Howes2012) and has a steeper perpendicular spectral index of approximately
![]() $-2.8$
(Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Chen et al.
Reference Chen, Horbury, Schekochihin, Wicks, Alexandrova and Mitchell2010; Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010).
$-2.8$
(Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Chen et al.
Reference Chen, Horbury, Schekochihin, Wicks, Alexandrova and Mitchell2010; Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010).
Since sheet-like structures are generically unstable to the tearing mode and the onset of magnetic reconnection, the formation of such structures by the large-scale Alfvénic turbulence immediately suggests that at some scale, the reconnection process may become faster than the dynamically aligning cascade, and disrupt the sheet-like structures. In resistive RMHD, the disruption scale was calculated by Mallet, Schekochihin & Chandran (Reference Mallet, Schekochihin and Chandran2017) and Loureiro & Boldyrev (Reference Loureiro and Boldyrev2017a
) as
![]() $\unicode[STIX]{x1D706}_{\text{D}}\sim L_{\bot }S_{L_{\bot }}^{-4/7}$
, where
$\unicode[STIX]{x1D706}_{\text{D}}\sim L_{\bot }S_{L_{\bot }}^{-4/7}$
, where
![]() $S_{L_{\bot }}\doteq L_{\bot }\overline{\unicode[STIX]{x1D6FF}z}/\unicode[STIX]{x1D702}$
is the outer-scale Lundquist number (equivalently, the magnetic Reynolds number),
$S_{L_{\bot }}\doteq L_{\bot }\overline{\unicode[STIX]{x1D6FF}z}/\unicode[STIX]{x1D702}$
is the outer-scale Lundquist number (equivalently, the magnetic Reynolds number),
![]() $\unicode[STIX]{x1D702}$
being the ohmic diffusivity (resistivity) . At scale
$\unicode[STIX]{x1D702}$
being the ohmic diffusivity (resistivity) . At scale
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, the sheet-like structures reconnect, and are converted into circularised flux ropes with radius
$\unicode[STIX]{x1D706}_{\text{D}}$
, the sheet-like structures reconnect, and are converted into circularised flux ropes with radius
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, destroying the dynamic alignment. Below
$\unicode[STIX]{x1D706}_{\text{D}}$
, destroying the dynamic alignment. Below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) proposed that these flux-rope-like structures realign and are disrupted again in a recursive fashion, leading to a steeper spectrum of approximately
$\unicode[STIX]{x1D706}_{\text{D}}$
, Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) proposed that these flux-rope-like structures realign and are disrupted again in a recursive fashion, leading to a steeper spectrum of approximately
![]() $k_{\bot }^{-11/5}$
and a final dissipative cutoff scale of
$k_{\bot }^{-11/5}$
and a final dissipative cutoff scale of
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D702}}\sim L_{\bot }S_{L_{\bot }}^{-3/4}$
Footnote
1
. This quantifies the role that reconnection plays in the dynamics of magnetohydrodynamic (MHD) turbulence, a topic that has a long history (Matthaeus & Lamkin Reference Matthaeus and Lamkin1986; Politano, Pouquet & Sulem Reference Politano, Pouquet and Sulem1989; Retinò et al.
Reference Retinò, Sundkvist, Vaivads, Mozer, André and Owen2007; Sundkvist et al.
Reference Sundkvist, Retinò, Vaivads and Bale2007; Servidio et al.
Reference Servidio, Matthaeus, Shay, Cassak and Dmitruk2009; Zhdankin et al.
Reference Zhdankin, Uzdensky, Perez and Boldyrev2013; Osman et al.
Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan2014; Greco et al.
Reference Greco, Perri, Servidio, Yordanova and Veltri2016; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017; Franci et al.
Reference Franci, Cerri, Califano, Landi, Papini, Verdini, Matteini, Jenko and Hellinger2017).
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D702}}\sim L_{\bot }S_{L_{\bot }}^{-3/4}$
Footnote
1
. This quantifies the role that reconnection plays in the dynamics of magnetohydrodynamic (MHD) turbulence, a topic that has a long history (Matthaeus & Lamkin Reference Matthaeus and Lamkin1986; Politano, Pouquet & Sulem Reference Politano, Pouquet and Sulem1989; Retinò et al.
Reference Retinò, Sundkvist, Vaivads, Mozer, André and Owen2007; Sundkvist et al.
Reference Sundkvist, Retinò, Vaivads and Bale2007; Servidio et al.
Reference Servidio, Matthaeus, Shay, Cassak and Dmitruk2009; Zhdankin et al.
Reference Zhdankin, Uzdensky, Perez and Boldyrev2013; Osman et al.
Reference Osman, Matthaeus, Gosling, Greco, Servidio, Hnat, Chapman and Phan2014; Greco et al.
Reference Greco, Perri, Servidio, Yordanova and Veltri2016; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017; Franci et al.
Reference Franci, Cerri, Califano, Landi, Papini, Verdini, Matteini, Jenko and Hellinger2017).
Here, we extend the Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) model of the disruption of Alfvénic turbulence by reconnection to the low-
![]() $\unicode[STIX]{x1D6FD}_{e}$
collisionless case, where the reconnection is enabled by electron inertia, rather than resistivity. The nature of the tearing mode in this regime is reviewed in § 3. Our main conclusion, arrived at in § 4, is that for sufficiently low electron beta
$\unicode[STIX]{x1D6FD}_{e}$
collisionless case, where the reconnection is enabled by electron inertia, rather than resistivity. The nature of the tearing mode in this regime is reviewed in § 3. Our main conclusion, arrived at in § 4, is that for sufficiently low electron beta
![]() $\unicode[STIX]{x1D6FD}_{e}=8\unicode[STIX]{x03C0}n_{e}T_{e}/B_{0}^{2}$
and large enough separation between the ion sound scale
$\unicode[STIX]{x1D6FD}_{e}=8\unicode[STIX]{x03C0}n_{e}T_{e}/B_{0}^{2}$
and large enough separation between the ion sound scale
![]() $\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}_{i}\sqrt{ZT_{e}/2T_{i}}\sim \unicode[STIX]{x1D70C}_{i}$
(we are assuming that
$\unicode[STIX]{x1D70C}_{s}=\unicode[STIX]{x1D70C}_{i}\sqrt{ZT_{e}/2T_{i}}\sim \unicode[STIX]{x1D70C}_{i}$
(we are assuming that
![]() $T_{e}\sim T_{i}$
) and the outer scale
$T_{e}\sim T_{i}$
) and the outer scale
![]() $L_{\bot }$
, the onset of reconnection may cause the turbulence to be disrupted, inducing a spectral break at a scale
$L_{\bot }$
, the onset of reconnection may cause the turbulence to be disrupted, inducing a spectral break at a scale
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
larger than the scale
$\unicode[STIX]{x1D706}_{\text{D}}$
larger than the scale
![]() $\sqrt{\unicode[STIX]{x1D70C}_{i}^{2}/2+\unicode[STIX]{x1D70C}_{s}^{2}}\sim \unicode[STIX]{x1D70C}_{i}\sim \unicode[STIX]{x1D70C}_{s}$
at which the Alfvén waves in this regime become dispersive (Zocco & Schekochihin Reference Zocco and Schekochihin2011). This means that the turbulent structures around the ion scale, which are the starting point for the kinetic Alfvén wave turbulent cascade at smaller scales, are created by tearing-induced disruption of the large-scale sheets produced by the RMHD turbulent dynamics, rather than solely by the change in the dispersion relation governing the linear wave response (cf. Cerri & Califano Reference Cerri and Califano2017; Franci et al.
Reference Franci, Cerri, Califano, Landi, Papini, Verdini, Matteini, Jenko and Hellinger2017).
$\sqrt{\unicode[STIX]{x1D70C}_{i}^{2}/2+\unicode[STIX]{x1D70C}_{s}^{2}}\sim \unicode[STIX]{x1D70C}_{i}\sim \unicode[STIX]{x1D70C}_{s}$
at which the Alfvén waves in this regime become dispersive (Zocco & Schekochihin Reference Zocco and Schekochihin2011). This means that the turbulent structures around the ion scale, which are the starting point for the kinetic Alfvén wave turbulent cascade at smaller scales, are created by tearing-induced disruption of the large-scale sheets produced by the RMHD turbulent dynamics, rather than solely by the change in the dispersion relation governing the linear wave response (cf. Cerri & Califano Reference Cerri and Califano2017; Franci et al.
Reference Franci, Cerri, Califano, Landi, Papini, Verdini, Matteini, Jenko and Hellinger2017).
In the solar wind at 1 AU, where
![]() $\unicode[STIX]{x1D6FD}_{e}\sim 1$
, we predict that only the most intense sheet-like structures are disrupted and converted into flux ropes. Interestingly, ‘Alfvén vortices’, which appear to be very similar to the flux-rope structures, have already been observed even in the solar wind at 1 AU (Lion, Alexandrova & Zaslavsky Reference Lion, Alexandrova and Zaslavsky2016; Perrone et al.
Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016). The mechanism proposed in this paper is a physical way to generate these structures. In § 5, we derive the fractional reduction in the volume filled by and energy contained within undisrupted, sheet-like structures at the ion sound scale as a function of
$\unicode[STIX]{x1D6FD}_{e}\sim 1$
, we predict that only the most intense sheet-like structures are disrupted and converted into flux ropes. Interestingly, ‘Alfvén vortices’, which appear to be very similar to the flux-rope structures, have already been observed even in the solar wind at 1 AU (Lion, Alexandrova & Zaslavsky Reference Lion, Alexandrova and Zaslavsky2016; Perrone et al.
Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016). The mechanism proposed in this paper is a physical way to generate these structures. In § 5, we derive the fractional reduction in the volume filled by and energy contained within undisrupted, sheet-like structures at the ion sound scale as a function of
![]() $\unicode[STIX]{x1D6FD}_{e}$
, showing that both these fractions decrease as
$\unicode[STIX]{x1D6FD}_{e}$
, showing that both these fractions decrease as
![]() $\unicode[STIX]{x1D6FD}_{e}$
decreases. We also derive the dependence of the amplitude of the newly formed flux ropes on their scale – this could be compared with the observed Alfvén vortices. Closer to the Sun, in the region to be explored by the Parker Solar Probe (Fox et al.
Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016), it is expected that, at least in fast-solar-wind streams,
$\unicode[STIX]{x1D6FD}_{e}$
decreases. We also derive the dependence of the amplitude of the newly formed flux ropes on their scale – this could be compared with the observed Alfvén vortices. Closer to the Sun, in the region to be explored by the Parker Solar Probe (Fox et al.
Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016), it is expected that, at least in fast-solar-wind streams,
![]() $\unicode[STIX]{x1D6FD}_{e}\approx 0.01$
(Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011), in which case the moderate-amplitude structures that dominate the energy spectrum may be disrupted. Thus, our results may be especially relevant to the turbulence that will be observed by this new mission. In § 6, we derive approximate scalings for the energy spectrum in the (very narrow) range between
$\unicode[STIX]{x1D6FD}_{e}\approx 0.01$
(Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011), in which case the moderate-amplitude structures that dominate the energy spectrum may be disrupted. Thus, our results may be especially relevant to the turbulence that will be observed by this new mission. In § 6, we derive approximate scalings for the energy spectrum in the (very narrow) range between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
, and show that it is somewhat steeper than
$\unicode[STIX]{x1D70C}_{s}$
, and show that it is somewhat steeper than
![]() $-3$
. In the appendix, we derive the disruption scale and the scalings for the energy spectrum in the ‘semicollisional’ case, where the reconnection is enabled by resistivity, but the diffusion layer is much thinner than the ion scale
$-3$
. In the appendix, we derive the disruption scale and the scalings for the energy spectrum in the ‘semicollisional’ case, where the reconnection is enabled by resistivity, but the diffusion layer is much thinner than the ion scale
![]() $\unicode[STIX]{x1D70C}_{s}$
– a situation that is relevant to many laboratory experiments, e.g. TREX (Forest et al.
Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015) and FLARE (Ji et al.
Reference Ji, Bhattacharjee, Prager, Daughton, Bale, Carter, Crocker, Drake, Egedal and Sarff2014), as well as in hybrid kinetic simulations (e.g. Parashar et al.
Reference Parashar, Shay, Cassak and Matthaeus2009; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017).
$\unicode[STIX]{x1D70C}_{s}$
– a situation that is relevant to many laboratory experiments, e.g. TREX (Forest et al.
Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015) and FLARE (Ji et al.
Reference Ji, Bhattacharjee, Prager, Daughton, Bale, Carter, Crocker, Drake, Egedal and Sarff2014), as well as in hybrid kinetic simulations (e.g. Parashar et al.
Reference Parashar, Shay, Cassak and Matthaeus2009; Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017).
2 Alfvénic turbulence model
In the theory of intermittent Alfvénic turbulence of Mallet & Schekochihin (Reference Mallet and Schekochihin2017), the turbulence is modelled as an ensemble of structures, each of which is characterised by an Elsasser amplitude
![]() $\unicode[STIX]{x1D6FF}z$
and three characteristic scales:
$\unicode[STIX]{x1D6FF}z$
and three characteristic scales:
![]() $l_{\Vert }$
(parallel),
$l_{\Vert }$
(parallel),
![]() $\unicode[STIX]{x1D706}$
(perpendicular) and
$\unicode[STIX]{x1D706}$
(perpendicular) and
![]() $\unicode[STIX]{x1D709}$
(fluctuation-direction). We normalise these variables by their values at the outer scale:
$\unicode[STIX]{x1D709}$
(fluctuation-direction). We normalise these variables by their values at the outer scale:
where
![]() $\overline{\unicode[STIX]{x1D6FF}z}$
is the outer-scale fluctuation amplitude, and
$\overline{\unicode[STIX]{x1D6FF}z}$
is the outer-scale fluctuation amplitude, and
![]() $L_{\bot }$
and
$L_{\bot }$
and
![]() $L_{\Vert }$
are the perpendicular and parallel outer scales. In the following, we will treat
$L_{\Vert }$
are the perpendicular and parallel outer scales. In the following, we will treat
![]() $\hat{\unicode[STIX]{x1D706}}$
as a parameter (i.e. we are conditioning on
$\hat{\unicode[STIX]{x1D706}}$
as a parameter (i.e. we are conditioning on
![]() $\hat{\unicode[STIX]{x1D706}}$
): the distribution of
$\hat{\unicode[STIX]{x1D706}}$
): the distribution of
![]() $\unicode[STIX]{x1D6FF}\hat{z}$
depends on
$\unicode[STIX]{x1D6FF}\hat{z}$
depends on
![]() $\hat{\unicode[STIX]{x1D706}}$
, and
$\hat{\unicode[STIX]{x1D706}}$
, and
![]() $\hat{\unicode[STIX]{x1D709}}$
and
$\hat{\unicode[STIX]{x1D709}}$
and
![]() $\hat{l}_{\Vert }$
are calculated from
$\hat{l}_{\Vert }$
are calculated from
![]() $\unicode[STIX]{x1D6FF}\hat{z}$
and
$\unicode[STIX]{x1D6FF}\hat{z}$
and
![]() $\hat{\unicode[STIX]{x1D706}}$
. It is assumed that the turbulence is critically balanced already at the outer scale. The normalised amplitude is given by
$\hat{\unicode[STIX]{x1D706}}$
. It is assumed that the turbulence is critically balanced already at the outer scale. The normalised amplitude is given by
where
![]() $q$
is a Poisson-distributed random variable,
$q$
is a Poisson-distributed random variable,
with mean
![]() $\unicode[STIX]{x1D707}=-\ln \hat{\unicode[STIX]{x1D706}}$
,Footnote
2
and
$\unicode[STIX]{x1D707}=-\ln \hat{\unicode[STIX]{x1D706}}$
,Footnote
2
and
![]() $\unicode[STIX]{x1D6EC}=1/\sqrt{2}$
is a dimensionless constant (which Mallet & Schekochihin Reference Mallet and Schekochihin2017 called
$\unicode[STIX]{x1D6EC}=1/\sqrt{2}$
is a dimensionless constant (which Mallet & Schekochihin Reference Mallet and Schekochihin2017 called
![]() $\unicode[STIX]{x1D6FD}$
, but which we here rename to avoid confusion with
$\unicode[STIX]{x1D6FD}$
, but which we here rename to avoid confusion with
![]() $\unicode[STIX]{x1D6FD}_{e}$
). The scalings of perpendicular structure functions are then given by
$\unicode[STIX]{x1D6FD}_{e}$
). The scalings of perpendicular structure functions are then given by
The fluctuation-direction scale
![]() $\hat{\unicode[STIX]{x1D709}}$
is related to the amplitude via
$\hat{\unicode[STIX]{x1D709}}$
is related to the amplitude via
while the parallel scale depends only on
![]() $\hat{\unicode[STIX]{x1D706}}$
:
$\hat{\unicode[STIX]{x1D706}}$
:
Following Mallet et al. (Reference Mallet, Schekochihin and Chandran2017), we define the ‘effective amplitude’ of structures that dominate the
![]() $n$
th-order perpendicular structure function:
$n$
th-order perpendicular structure function:
The effective amplitude
![]() $\unicode[STIX]{x1D6FF}\hat{z}[n]$
is a strictly increasing function of
$\unicode[STIX]{x1D6FF}\hat{z}[n]$
is a strictly increasing function of
![]() $n$
, and so
$n$
, and so
![]() $n$
may be used as a convenient proxy for the amplitude of the structures at a given scale. The scalings for three interesting cases can be immediately obtained from (2.7): first,
$n$
may be used as a convenient proxy for the amplitude of the structures at a given scale. The scalings for three interesting cases can be immediately obtained from (2.7): first,
describes the ‘most intense’ structures, whose amplitude is independent of scale; secondly,
describes the fluctuations that dominate the second-order structure function and the energy spectrum, and thus determine the spectral index; finally, the ‘bulk’ fluctuations are described by
![]() $n\rightarrow 0$
, and their amplitudes scale as
$n\rightarrow 0$
, and their amplitudes scale as
We will also need an expression for the (effective) fluctuation-direction scale for the
![]() $n$
th-order fluctuations, given by
$n$
th-order fluctuations, given by
and for the cascade time,
One can easily see from (2.11) that the structures are anisotropic in the perpendicular plane, with
![]() $\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
, and that the higher-amplitude structures are more anisotropic, consistent with numerical evidence (Mallet et al.
Reference Mallet, Schekochihin and Chandran2015, Reference Mallet, Schekochihin, Chandran, Chen, Horbury, Wicks and Greenan2016).
$\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
, and that the higher-amplitude structures are more anisotropic, consistent with numerical evidence (Mallet et al.
Reference Mallet, Schekochihin and Chandran2015, Reference Mallet, Schekochihin, Chandran, Chen, Horbury, Wicks and Greenan2016).
We now have all the information needed about the turbulent structures to determine whether they can be disrupted by tearing.
3 Collisionless tearing mode
Scalings for the low-
![]() $\unicode[STIX]{x1D6FD}_{e}$
collisionless tearing mode are reviewed in appendix B.3 of Zocco & Schekochihin (Reference Zocco and Schekochihin2011). Our sheet-like turbulent structures have a width
$\unicode[STIX]{x1D6FD}_{e}$
collisionless tearing mode are reviewed in appendix B.3 of Zocco & Schekochihin (Reference Zocco and Schekochihin2011). Our sheet-like turbulent structures have a width
![]() $\unicode[STIX]{x1D706}$
and a length
$\unicode[STIX]{x1D706}$
and a length
![]() $\unicode[STIX]{x1D709}$
in the perpendicular plane. We will assume that the perturbed magnetic field reverses across the structure
$\unicode[STIX]{x1D709}$
in the perpendicular plane. We will assume that the perturbed magnetic field reverses across the structure
![]() $\unicode[STIX]{x1D6FF}b\sim \unicode[STIX]{x1D6FF}z$
. There is also a velocity perturbation
$\unicode[STIX]{x1D6FF}b\sim \unicode[STIX]{x1D6FF}z$
. There is also a velocity perturbation
![]() $\unicode[STIX]{x1D6FF}u$
associated with the
$\unicode[STIX]{x1D6FF}u$
associated with the
![]() $\unicode[STIX]{x1D6FF}z$
. If the situation were that
$\unicode[STIX]{x1D6FF}z$
. If the situation were that
![]() $\unicode[STIX]{x1D6FF}u>\unicode[STIX]{x1D6FF}b$
, the Kelvin–Helmholtz instability would disrupt the sheets much faster than the tearing mode. However, this situation does not typically occur, because the vortex stretching terms for the different Elsasser fields
$\unicode[STIX]{x1D6FF}u>\unicode[STIX]{x1D6FF}b$
, the Kelvin–Helmholtz instability would disrupt the sheets much faster than the tearing mode. However, this situation does not typically occur, because the vortex stretching terms for the different Elsasser fields
![]() $\boldsymbol{z}_{\bot }^{\pm }$
have opposite sign (Zhdankin, Boldyrev & Uzdensky Reference Zhdankin, Boldyrev and Uzdensky2016), meaning that ‘current sheets’ are more common than ‘shear layers’ in RMHD turbulence, i.e.
$\boldsymbol{z}_{\bot }^{\pm }$
have opposite sign (Zhdankin, Boldyrev & Uzdensky Reference Zhdankin, Boldyrev and Uzdensky2016), meaning that ‘current sheets’ are more common than ‘shear layers’ in RMHD turbulence, i.e.
![]() $\unicode[STIX]{x1D6FF}u<\unicode[STIX]{x1D6FF}b$
(this is also true in the solar wind; see, e.g. Chen Reference Chen2016, Wicks et al.
Reference Wicks, Mallet, Horbury, Chen, Schekochihin and Mitchell2013), and the Kelvin–Helmholtz instability is naturally stabilised (Chandrasekhar Reference Chandrasekhar1961). For simplicity, we assume that the velocity fluctuations
$\unicode[STIX]{x1D6FF}u<\unicode[STIX]{x1D6FF}b$
(this is also true in the solar wind; see, e.g. Chen Reference Chen2016, Wicks et al.
Reference Wicks, Mallet, Horbury, Chen, Schekochihin and Mitchell2013), and the Kelvin–Helmholtz instability is naturally stabilised (Chandrasekhar Reference Chandrasekhar1961). For simplicity, we assume that the velocity fluctuations
![]() $\unicode[STIX]{x1D6FF}u\lesssim \unicode[STIX]{x1D6FF}b$
present in the sheet-like structures do not significantly affect the dynamics that we will describe in this paper.
$\unicode[STIX]{x1D6FF}u\lesssim \unicode[STIX]{x1D6FF}b$
present in the sheet-like structures do not significantly affect the dynamics that we will describe in this paper.
The structure of the collisionless tearing mode involves three scales: the perpendicular scale
![]() $\unicode[STIX]{x1D706}$
of the turbulent structure, and a nested inner layer, where two-fluid effects become important at the ion sound scale
$\unicode[STIX]{x1D706}$
of the turbulent structure, and a nested inner layer, where two-fluid effects become important at the ion sound scale
![]() $\unicode[STIX]{x1D70C}_{s}$
, while flux unfreezing happens due to electron inertia in a thinner layer controlled by the electron inertial scale
$\unicode[STIX]{x1D70C}_{s}$
, while flux unfreezing happens due to electron inertia in a thinner layer controlled by the electron inertial scale
![]() $d_{e}=c/\unicode[STIX]{x1D714}_{pe}\ll \unicode[STIX]{x1D70C}_{s}$
, where
$d_{e}=c/\unicode[STIX]{x1D714}_{pe}\ll \unicode[STIX]{x1D70C}_{s}$
, where
![]() $\unicode[STIX]{x1D714}_{pe}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$
is the electron plasma frequency. The tearing instability’s growth rates will, therefore, involve all of these scales. The scalings that we use here will cease to apply if
$\unicode[STIX]{x1D714}_{pe}=\sqrt{4\unicode[STIX]{x03C0}n_{e}e^{2}/m_{e}}$
is the electron plasma frequency. The tearing instability’s growth rates will, therefore, involve all of these scales. The scalings that we use here will cease to apply if
![]() $\unicode[STIX]{x1D70C}_{s}\lesssim d_{e}$
(i.e.
$\unicode[STIX]{x1D70C}_{s}\lesssim d_{e}$
(i.e.
![]() $\unicode[STIX]{x1D6FD}_{e}\lesssim m_{e}/m_{i}$
), at which point the ion scale becomes unimportant, and if
$\unicode[STIX]{x1D6FD}_{e}\lesssim m_{e}/m_{i}$
), at which point the ion scale becomes unimportant, and if
![]() $\unicode[STIX]{x1D6FD}_{e}\gtrsim 1$
, when the flux unfreezing happens at the electron gyroradius
$\unicode[STIX]{x1D6FD}_{e}\gtrsim 1$
, when the flux unfreezing happens at the electron gyroradius
![]() $\unicode[STIX]{x1D70C}_{e}=d_{e}\sqrt{\unicode[STIX]{x1D6FD}_{e}}$
, rather than at
$\unicode[STIX]{x1D70C}_{e}=d_{e}\sqrt{\unicode[STIX]{x1D6FD}_{e}}$
, rather than at
![]() $d_{e}$
. This means that we are restricting ourselves to ‘moderately’ small beta,
$d_{e}$
. This means that we are restricting ourselves to ‘moderately’ small beta,
![]() $1\gg \unicode[STIX]{x1D6FD}_{e}\gg m_{e}/m_{i}$
.
$1\gg \unicode[STIX]{x1D6FD}_{e}\gg m_{e}/m_{i}$
.
We will assume a Harris-sheet-like equilibrium (Harris Reference Harris1962)Footnote
3
. For long-wavelength modes (
![]() $k\ll 1/\unicode[STIX]{x1D706}$
), the instability parameter
$k\ll 1/\unicode[STIX]{x1D706}$
), the instability parameter
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
is given by
$\unicode[STIX]{x1D6E5}^{\prime }$
is given by
For
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\ll 1$
, where
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\ll 1$
, where
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}$
is the width of the inner layer, the linear growth rate and the inner-layer width are
$\unicode[STIX]{x1D6FF}_{\text{in}}$
is the width of the inner layer, the linear growth rate and the inner-layer width are
For
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$
, they are
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$
, they are
The wavenumber
![]() $k_{\text{tr}}$
of the transition between these two regimes can be found by balancing the two expressions for the growth rate, giving
$k_{\text{tr}}$
of the transition between these two regimes can be found by balancing the two expressions for the growth rate, giving
For
![]() $k<k_{\text{tr}}$
, the growth rate is
$k<k_{\text{tr}}$
, the growth rate is
![]() $\unicode[STIX]{x1D6FE}_{{<}}$
, while for
$\unicode[STIX]{x1D6FE}_{{<}}$
, while for
![]() $k>k_{\text{tr}}$
, it is
$k>k_{\text{tr}}$
, it is
![]() $\unicode[STIX]{x1D6FE}_{{>}}$
, which is independent of wavenumber. This breaks down when
$\unicode[STIX]{x1D6FE}_{{>}}$
, which is independent of wavenumber. This breaks down when
![]() $k\sim 1/\unicode[STIX]{x1D706}$
, because (3.1) ceases to apply – but, since
$k\sim 1/\unicode[STIX]{x1D706}$
, because (3.1) ceases to apply – but, since
![]() $\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
, this only happens for a very large number of islands. Therefore, the maximum growth rate is attained for all
$\unicode[STIX]{x1D709}\gg \unicode[STIX]{x1D706}$
, this only happens for a very large number of islands. Therefore, the maximum growth rate is attained for all
![]() $k>k_{\text{tr}}$
, and is given simply by
$k>k_{\text{tr}}$
, and is given simply by
![]() $\unicode[STIX]{x1D6FE}_{{>}}$
. Thus there is always a mode with the maximum growth rate and a large enough wavenumber to fit into a sheet of any length
$\unicode[STIX]{x1D6FE}_{{>}}$
. Thus there is always a mode with the maximum growth rate and a large enough wavenumber to fit into a sheet of any length
![]() $\unicode[STIX]{x1D709}>\unicode[STIX]{x1D706}$
. This is somewhat different from the resistive-RMHD case studied by Mallet et al. (Reference Mallet, Schekochihin and Chandran2017), in which
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D706}$
. This is somewhat different from the resistive-RMHD case studied by Mallet et al. (Reference Mallet, Schekochihin and Chandran2017), in which
![]() $\unicode[STIX]{x1D6FE}_{{>}}^{\text{RMHD}}\propto k^{-2/5}$
, while
$\unicode[STIX]{x1D6FE}_{{>}}^{\text{RMHD}}\propto k^{-2/5}$
, while
![]() $\unicode[STIX]{x1D6FE}_{{<}}^{\text{RMHD}}\propto k^{2/3}$
, and the maximum growth rate is attained at the transitional wavenumber.
$\unicode[STIX]{x1D6FE}_{{<}}^{\text{RMHD}}\propto k^{2/3}$
, and the maximum growth rate is attained at the transitional wavenumber.
The linear growth stage of tearing ends when the width of the islands reaches
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}$
, which decreases with increasing
$\unicode[STIX]{x1D6FF}_{\text{in}}$
, which decreases with increasing
![]() $k$
for
$k$
for
![]() $k>k_{\text{tr}}$
. Thus at the end of the linear stage, the largest islands are produced by the mode with
$k>k_{\text{tr}}$
. Thus at the end of the linear stage, the largest islands are produced by the mode with
![]() $k\sim k_{\text{tr}}$
, and so, despite the independence of the linear growth rate on
$k\sim k_{\text{tr}}$
, and so, despite the independence of the linear growth rate on
![]() $k$
, we can assume that this transitional mode dominates the nonlinear dynamics. We assume that the
$k$
, we can assume that this transitional mode dominates the nonlinear dynamics. We assume that the
![]() $X$
-points between the islands then collapse quickly (i.e. on a time scale at most comparable to
$X$
-points between the islands then collapse quickly (i.e. on a time scale at most comparable to
![]() $\unicode[STIX]{x1D6FE}_{{>}}^{-1}$
), circularising the islands and forming a set of flux ropes of width
$\unicode[STIX]{x1D6FE}_{{>}}^{-1}$
), circularising the islands and forming a set of flux ropes of width
![]() $\unicode[STIX]{x1D706}$
, as appears to be consistent with numerical evidence (Loureiro, Schekochihin & Zocco Reference Loureiro, Schekochihin and Zocco2013).Footnote
4
Since these structures are as wide as the original sheet, the latter should at this point be disrupted and broken up – being effectively replaced by a set of flux ropes. The scale of these ropes parallel to the (exact) magnetic field is set as usual by critical balance. Since we assume that the
$\unicode[STIX]{x1D706}$
, as appears to be consistent with numerical evidence (Loureiro, Schekochihin & Zocco Reference Loureiro, Schekochihin and Zocco2013).Footnote
4
Since these structures are as wide as the original sheet, the latter should at this point be disrupted and broken up – being effectively replaced by a set of flux ropes. The scale of these ropes parallel to the (exact) magnetic field is set as usual by critical balance. Since we assume that the
![]() $X$
-point collapse is at least as fast as the linear tearing stage, we estimate the disruption time using the linear growth rate (3.2) of the tearing mode:
$X$
-point collapse is at least as fast as the linear tearing stage, we estimate the disruption time using the linear growth rate (3.2) of the tearing mode:
It is important to point out that the restriction to low
![]() $\unicode[STIX]{x1D6FD}_{e}$
limits the applicability of our conclusions in the solar wind, where, more often than not,
$\unicode[STIX]{x1D6FD}_{e}$
limits the applicability of our conclusions in the solar wind, where, more often than not,
![]() $\unicode[STIX]{x1D6FD}_{e}\sim 1$
, but our results will be more relevant to the turbulence closer to the Sun and in the corona: indeed, at the perihelion (approximately 10 solar radii) of the upcoming Parker Solar Probe mission,
$\unicode[STIX]{x1D6FD}_{e}\sim 1$
, but our results will be more relevant to the turbulence closer to the Sun and in the corona: indeed, at the perihelion (approximately 10 solar radii) of the upcoming Parker Solar Probe mission,
![]() $\unicode[STIX]{x1D6FD}_{e}\approx 0.01$
, at least in fast solar-wind streams (Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). Moreover, the growth rate scaling (3.2) appears to be quite robust even at moderately large
$\unicode[STIX]{x1D6FD}_{e}\approx 0.01$
, at least in fast solar-wind streams (Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). Moreover, the growth rate scaling (3.2) appears to be quite robust even at moderately large
![]() $\unicode[STIX]{x1D6FD}_{e}$
: Numata & Loureiro (Reference Numata and Loureiro2015) showed that, keeping all other parameters fixed,
$\unicode[STIX]{x1D6FD}_{e}$
: Numata & Loureiro (Reference Numata and Loureiro2015) showed that, keeping all other parameters fixed,
![]() $\unicode[STIX]{x1D6FE}_{{>}}\propto \unicode[STIX]{x1D6FD}_{e}^{-1/2}\propto d_{e}$
up to at least
$\unicode[STIX]{x1D6FE}_{{>}}\propto \unicode[STIX]{x1D6FD}_{e}^{-1/2}\propto d_{e}$
up to at least
![]() $\unicode[STIX]{x1D6FD}_{e}=10$
, in agreement with (3.2), and despite the width of the reconnecting layer being set by
$\unicode[STIX]{x1D6FD}_{e}=10$
, in agreement with (3.2), and despite the width of the reconnecting layer being set by
![]() $\unicode[STIX]{x1D70C}_{e}$
rather than
$\unicode[STIX]{x1D70C}_{e}$
rather than
![]() $d_{e}$
. Therefore, we expect our conclusions to be at least qualitatively relevant at
$d_{e}$
. Therefore, we expect our conclusions to be at least qualitatively relevant at
![]() $\unicode[STIX]{x1D6FD}_{e}\sim 1$
.
$\unicode[STIX]{x1D6FD}_{e}\sim 1$
.
4 Disruption scale
A sheet-like structure will be disrupted if its nonlinear cascade time (2.12) is longer than its disruption time (3.5). The disruption scale
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
is then determined by demanding
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
is then determined by demanding
Using (2.11) and (2.7), we find that, for
![]() $n$
th-order aligned structures, this inequality is satisfied for
$n$
th-order aligned structures, this inequality is satisfied for
The scale
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
is an increasing function of
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
is an increasing function of
![]() $n$
. It is largest for the most intense structures, with
$n$
. It is largest for the most intense structures, with
![]() $n\rightarrow \infty$
, for which
$n\rightarrow \infty$
, for which
The scale at which the
![]() $n=2$
structures, which determine the scaling of the second-order structure function and the energy spectrum, are disrupted isFootnote
5
$n=2$
structures, which determine the scaling of the second-order structure function and the energy spectrum, are disrupted isFootnote
5
and, finally, the bulk fluctuations (
![]() $n\rightarrow 0$
) are disrupted at
$n\rightarrow 0$
) are disrupted at
The disruption may effectively be thought of as taking place over a narrow range of scales between
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[\infty ]$
and
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[\infty ]$
and
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[0]$
, with
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[0]$
, with
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
as a good representative. The disruption will only be relevant if any of these scales is larger than the scale at which the waves become dispersive, i.e.
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
as a good representative. The disruption will only be relevant if any of these scales is larger than the scale at which the waves become dispersive, i.e.
 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D706}_{\text{D}}[n]}{\unicode[STIX]{x1D70C}_{s}} & {\sim} & \displaystyle \left(\frac{d_{e}}{\unicode[STIX]{x1D70C}_{s}}\right)^{(2/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\left(\frac{L_{\bot }}{\unicode[STIX]{x1D70C}_{s}}\right)^{1-(4/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}},\nonumber\\ \displaystyle & {\sim} & \displaystyle \left(\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D6FD}_{e}}{Z}\right)^{-(1/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\left(\frac{L_{\bot }}{\unicode[STIX]{x1D70C}_{s}}\right)^{1-(4/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\gtrsim 1.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D706}_{\text{D}}[n]}{\unicode[STIX]{x1D70C}_{s}} & {\sim} & \displaystyle \left(\frac{d_{e}}{\unicode[STIX]{x1D70C}_{s}}\right)^{(2/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\left(\frac{L_{\bot }}{\unicode[STIX]{x1D70C}_{s}}\right)^{1-(4/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}},\nonumber\\ \displaystyle & {\sim} & \displaystyle \left(\frac{m_{i}}{m_{e}}\frac{\unicode[STIX]{x1D6FD}_{e}}{Z}\right)^{-(1/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\left(\frac{L_{\bot }}{\unicode[STIX]{x1D70C}_{s}}\right)^{1-(4/5)(1-2\unicode[STIX]{x1D701}_{n}^{\bot }/5n)^{-1}}\gtrsim 1.\end{eqnarray}$$
This gives us a critical
![]() $\unicode[STIX]{x1D6FD}_{e}$
for structures at any given
$\unicode[STIX]{x1D6FD}_{e}$
for structures at any given
![]() $n$
to be disrupted:
$n$
to be disrupted:
For the
![]() $n=2$
structures,
$n=2$
structures,
while for the most intense fluctuations (
![]() $n\rightarrow \infty$
),
$n\rightarrow \infty$
),
It is interesting to note that, despite the fact that the dependence of
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[n]$
on
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[n]$
on
![]() $n$
does not appear to be very strong [the exponents in (4.3), (4.4) and (4.5) are close together, at
$n$
does not appear to be very strong [the exponents in (4.3), (4.4) and (4.5) are close together, at
![]() $0.40$
,
$0.40$
,
![]() $0.44$
and
$0.44$
and
![]() $0.46$
respectively], the dependence of
$0.46$
respectively], the dependence of
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
on
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
is a strong function of
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
is a strong function of
![]() $n$
.
$n$
.
In the solar wind, typically
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}\approx 10^{3}$
(Chen Reference Chen2016), and so
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}\approx 10^{3}$
(Chen Reference Chen2016), and so
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[2]\sim 10^{-2}$
, which is rare at 1 AU but should be rather common closer to the Sun in the region to be explored by the Parker Solar Probe (Fox et al.
Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). On the other hand,
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[2]\sim 10^{-2}$
, which is rare at 1 AU but should be rather common closer to the Sun in the region to be explored by the Parker Solar Probe (Fox et al.
Reference Fox, Velli, Bale, Decker, Driesman, Howard, Kasper, Kinnison, Kusterer and Lario2016; Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011). On the other hand,
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[\infty ]\sim 1$
, and so one might expect the most intense sheet-like structures to become unstable to the onset of reconnection even at moderate
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[\infty ]\sim 1$
, and so one might expect the most intense sheet-like structures to become unstable to the onset of reconnection even at moderate
![]() $\unicode[STIX]{x1D6FD}_{e}$
. Flux-rope-like ‘Alfvén vortex’ structures extended in the parallel direction were indeed observed at ion scales in the solar wind by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016) and Lion et al. (Reference Lion, Alexandrova and Zaslavsky2016). It is tempting to identify the structures produced by the disruption due to tearing with these observationsFootnote
6
. We will study the structures produced by the disruption process in the next section, quantifying the relationship between their amplitude and scale, and further examining their importance as a function of
$\unicode[STIX]{x1D6FD}_{e}$
. Flux-rope-like ‘Alfvén vortex’ structures extended in the parallel direction were indeed observed at ion scales in the solar wind by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016) and Lion et al. (Reference Lion, Alexandrova and Zaslavsky2016). It is tempting to identify the structures produced by the disruption due to tearing with these observationsFootnote
6
. We will study the structures produced by the disruption process in the next section, quantifying the relationship between their amplitude and scale, and further examining their importance as a function of
![]() $\unicode[STIX]{x1D6FD}_{e}$
and of
$\unicode[STIX]{x1D6FD}_{e}$
and of
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
.
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
.
Finally, let us set aside for a moment the precise values of
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
for which we predict that disruption happens, and focus instead on the scaling of the break in the energy spectrum,
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
for which we predict that disruption happens, and focus instead on the scaling of the break in the energy spectrum,
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
, with physical parameters, i.e. the dependence of
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
, with physical parameters, i.e. the dependence of
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
on
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[2]$
on
![]() $\unicode[STIX]{x1D6FD}$
. Chen et al. (Reference Chen, Leung, Boldyrev, Maruca and Bale2014) observed that at low
$\unicode[STIX]{x1D6FD}$
. Chen et al. (Reference Chen, Leung, Boldyrev, Maruca and Bale2014) observed that at low
![]() $\unicode[STIX]{x1D6FD}_{i}$
, the break scale of solar-wind turbulence appeared to scale as
$\unicode[STIX]{x1D6FD}_{i}$
, the break scale of solar-wind turbulence appeared to scale as
![]() $d_{i}\propto \unicode[STIX]{x1D70C}_{i}/\sqrt{\unicode[STIX]{x1D6FD}_{i}}$
, in contradiction with expectations based on the linear physics of low-
$d_{i}\propto \unicode[STIX]{x1D70C}_{i}/\sqrt{\unicode[STIX]{x1D6FD}_{i}}$
, in contradiction with expectations based on the linear physics of low-
![]() $\unicode[STIX]{x1D6FD}$
plasmas (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Here we predict (ignoring the factor of
$\unicode[STIX]{x1D6FD}$
plasmas (Schekochihin et al.
Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Here we predict (ignoring the factor of
![]() $(L_{\bot }/\unicode[STIX]{x1D70C}_{s})^{1/9}$
, which barely changes with the relevant physical parameters)
$(L_{\bot }/\unicode[STIX]{x1D70C}_{s})^{1/9}$
, which barely changes with the relevant physical parameters)
For disruption due to reconnection to explain the anomalous break scale observed by Chen et al. (Reference Chen, Leung, Boldyrev, Maruca and Bale2014), there would therefore have to be correlations between
![]() $\unicode[STIX]{x1D6FD}_{i}$
and
$\unicode[STIX]{x1D6FD}_{i}$
and
![]() $T_{e}/T_{i}$
in their chosen intervals (namely,
$T_{e}/T_{i}$
in their chosen intervals (namely,
![]() $T_{i}/T_{e}\propto \unicode[STIX]{x1D6FD}_{i}$
to match precisely). Encouragingly, in their data it does appear that the lower-
$T_{i}/T_{e}\propto \unicode[STIX]{x1D6FD}_{i}$
to match precisely). Encouragingly, in their data it does appear that the lower-
![]() $\unicode[STIX]{x1D6FD}_{i}$
intervals are associated with markedly higher
$\unicode[STIX]{x1D6FD}_{i}$
intervals are associated with markedly higher
![]() $T_{e}/T_{i}$
.
$T_{e}/T_{i}$
.
5 Statistical properties of flux ropes
The dependence (4.2) of
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
on
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}$
on
![]() $n$
is one way of quantifying the scales at which the disrupted structures appear. In this section, we recast our calculation, treating the amplitude of the fluctuation as a random variable, i.e. we return to (2.2), and determine what fraction of the aligned structures remain undisrupted at any given scale, in terms of
$n$
is one way of quantifying the scales at which the disrupted structures appear. In this section, we recast our calculation, treating the amplitude of the fluctuation as a random variable, i.e. we return to (2.2), and determine what fraction of the aligned structures remain undisrupted at any given scale, in terms of
![]() $q$
(we remind the reader that this is an integer distributed as a Poisson random variable with mean
$q$
(we remind the reader that this is an integer distributed as a Poisson random variable with mean
![]() $\langle q\rangle =\unicode[STIX]{x1D707}=-\ln \hat{\unicode[STIX]{x1D706}}$
). For a structure to be disrupted, we again demand (4.1) and, using (2.5), find that
$\langle q\rangle =\unicode[STIX]{x1D707}=-\ln \hat{\unicode[STIX]{x1D706}}$
). For a structure to be disrupted, we again demand (4.1) and, using (2.5), find that
This is satisfied for
 $$\begin{eqnarray}\displaystyle \displaystyle q\lesssim q_{\text{D}} & = & \displaystyle \frac{(5/2)\ln \hat{\unicode[STIX]{x1D706}}-\ln \left(d_{e}\unicode[STIX]{x1D70C}_{s}/L_{\bot }^{2}\right)}{\ln \unicode[STIX]{x1D6EC}}\nonumber\\ \displaystyle \displaystyle & = & \displaystyle \frac{(5/2)\ln \hat{\unicode[STIX]{x1D706}}-2\ln \left(\unicode[STIX]{x1D70C}_{s}/L_{\bot }\right)+(1/2)\ln \left(\unicode[STIX]{x1D6FD}_{e}m_{i}/Zm_{e}\right)}{\ln \unicode[STIX]{x1D6EC}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \displaystyle q\lesssim q_{\text{D}} & = & \displaystyle \frac{(5/2)\ln \hat{\unicode[STIX]{x1D706}}-\ln \left(d_{e}\unicode[STIX]{x1D70C}_{s}/L_{\bot }^{2}\right)}{\ln \unicode[STIX]{x1D6EC}}\nonumber\\ \displaystyle \displaystyle & = & \displaystyle \frac{(5/2)\ln \hat{\unicode[STIX]{x1D706}}-2\ln \left(\unicode[STIX]{x1D70C}_{s}/L_{\bot }\right)+(1/2)\ln \left(\unicode[STIX]{x1D6FD}_{e}m_{i}/Zm_{e}\right)}{\ln \unicode[STIX]{x1D6EC}}.\end{eqnarray}$$
5.1 Filling factor of aligned turbulence
At any given scale, the filling factor of sheet-like, aligned structures that have not been affected by the disruption process (i.e. the probability of encountering them) is given by
where the distribution of
![]() $q$
is given by (2.3). Similarly, the disruption causes a fractional reduction of energy contained in aligned sheet-like structures that is, using (2.4) and (2.2),
$q$
is given by (2.3). Similarly, the disruption causes a fractional reduction of energy contained in aligned sheet-like structures that is, using (2.4) and (2.2),
Obviously, (5.3) and (5.4) can only be considered quantitatively good estimates if
![]() $f_{0}$
and
$f_{0}$
and
![]() $f_{2}$
are close to unity, i.e. if the overall ‘RMHD ensemble’ (described in § 2) is not significantly altered.
$f_{2}$
are close to unity, i.e. if the overall ‘RMHD ensemble’ (described in § 2) is not significantly altered.
Using (5.2), both
![]() $f_{0}$
and
$f_{0}$
and
![]() $f_{2}$
may be calculated numerically, as functions of
$f_{2}$
may be calculated numerically, as functions of
![]() $\hat{\unicode[STIX]{x1D706}}$
,
$\hat{\unicode[STIX]{x1D706}}$
,
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, and
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, and
![]() $\unicode[STIX]{x1D6FD}_{e}$
. A particularly interesting case is
$\unicode[STIX]{x1D6FD}_{e}$
. A particularly interesting case is
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}_{s}$
, since this quantifies the cumulative effect of reconnection on the turbulence at the ion scale. Figure 1 shows the dependence of
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D70C}_{s}$
, since this quantifies the cumulative effect of reconnection on the turbulence at the ion scale. Figure 1 shows the dependence of
![]() $f_{0}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
and
$f_{0}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
and
![]() $f_{2}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
on
$f_{2}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
on
![]() $\unicode[STIX]{x1D6FD}_{e}$
. The effect of disruption becomes more important at smaller
$\unicode[STIX]{x1D6FD}_{e}$
. The effect of disruption becomes more important at smaller
![]() $\unicode[STIX]{x1D6FD}_{e}$
. Note that the amount of energy in the undisrupted structures at the ion scale is significantly reduced for values of
$\unicode[STIX]{x1D6FD}_{e}$
. Note that the amount of energy in the undisrupted structures at the ion scale is significantly reduced for values of
![]() $\unicode[STIX]{x1D6FD}_{e}$
somewhat larger than
$\unicode[STIX]{x1D6FD}_{e}$
somewhat larger than
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[2]$
given by (4.8). This suggests that, in practice, the turbulence is significantly affected by the disruption at only moderately small
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[2]$
given by (4.8). This suggests that, in practice, the turbulence is significantly affected by the disruption at only moderately small
![]() $\unicode[STIX]{x1D6FD}_{e}$
: e.g. for
$\unicode[STIX]{x1D6FD}_{e}$
: e.g. for
![]() $\unicode[STIX]{x1D6FD}_{e}\sim 0.1$
, only around half of the energy that would be in sheets without disruption actually makes it to the ion scale, despite only approximately
$\unicode[STIX]{x1D6FD}_{e}\sim 0.1$
, only around half of the energy that would be in sheets without disruption actually makes it to the ion scale, despite only approximately
![]() $10\,\%$
by volume of the turbulence being disrupted.
$10\,\%$
by volume of the turbulence being disrupted.
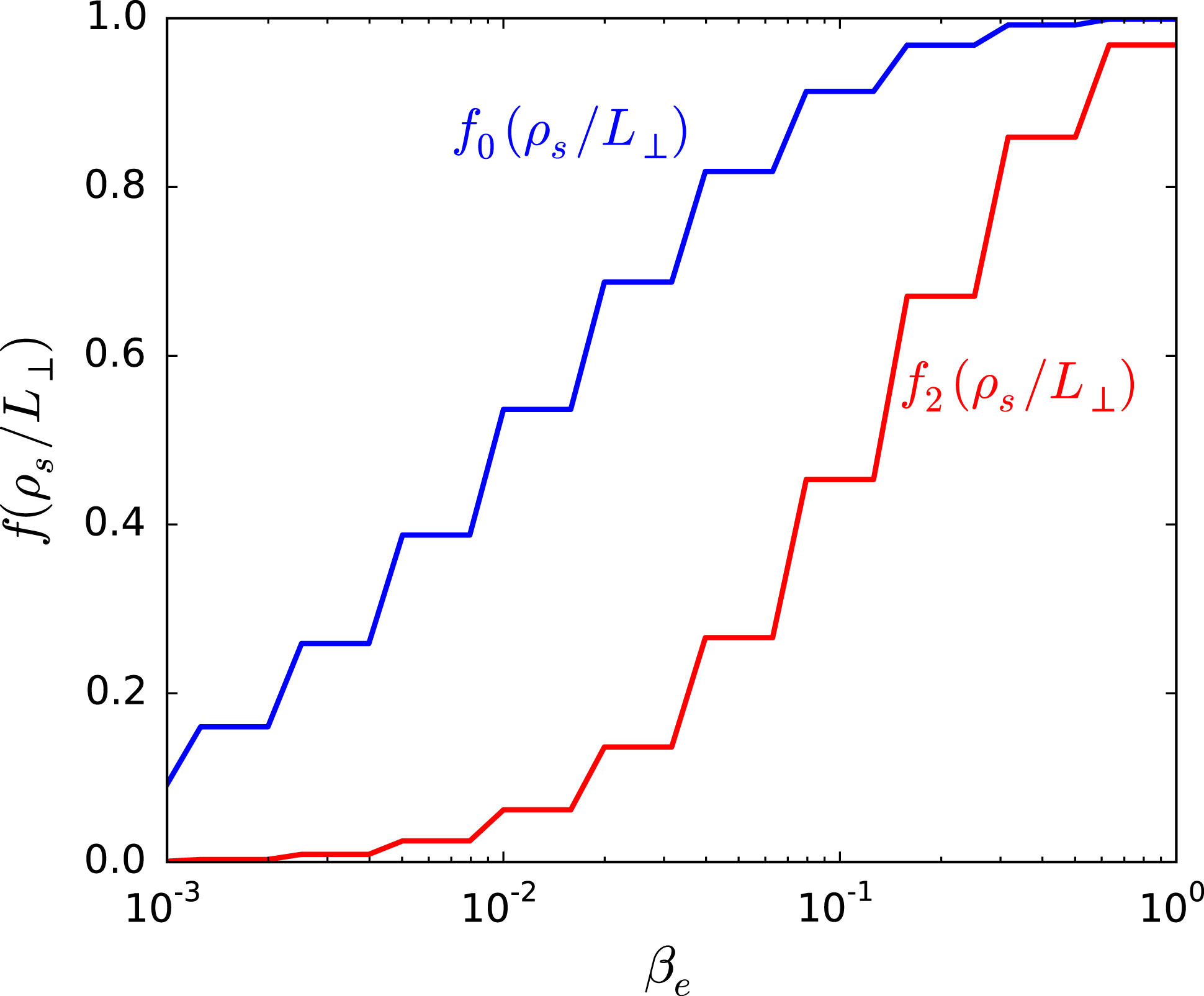
Figure 1. The filling factor of the aligned (i.e. undisrupted) structures at the ion sound scale
![]() $f_{0}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
(blue) and fraction
$f_{0}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
(blue) and fraction
![]() $f_{2}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
of energy in them (red), plotted as a function of
$f_{2}(\unicode[STIX]{x1D70C}_{s}/L_{\bot })$
of energy in them (red), plotted as a function of
![]() $\unicode[STIX]{x1D6FD}_{e}$
. We have taken
$\unicode[STIX]{x1D6FD}_{e}$
. We have taken
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }=10^{-3}$
, a reasonable value for the solar wind. Since
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }=10^{-3}$
, a reasonable value for the solar wind. Since
![]() $q$
is an integer but
$q$
is an integer but
![]() $q_{\text{D}}$
is not, the sums (5.3) and (5.4) are performed up to
$q_{\text{D}}$
is not, the sums (5.3) and (5.4) are performed up to
![]() $\lfloor q_{\text{D}}\rfloor$
, resulting in the discontinuities shown in the plot. In reality, of course,
$\lfloor q_{\text{D}}\rfloor$
, resulting in the discontinuities shown in the plot. In reality, of course,
![]() $f_{0}$
and
$f_{0}$
and
![]() $f_{2}$
will be smooth.
$f_{2}$
will be smooth.
5.2 Amplitude of flux ropes
We have proposed that the sheet-like structures with
![]() $q\sim q_{\text{D}}$
disrupted by tearing at the scale
$q\sim q_{\text{D}}$
disrupted by tearing at the scale
![]() $\unicode[STIX]{x1D706}$
are converted into circular flux ropes, with perpendicular scale
$\unicode[STIX]{x1D706}$
are converted into circular flux ropes, with perpendicular scale
![]() $\unicode[STIX]{x1D706}$
. We will assume that, just after they are created, they have the same amplitude as the sheet-like structure that produced them:
$\unicode[STIX]{x1D706}$
. We will assume that, just after they are created, they have the same amplitude as the sheet-like structure that produced them:
The flux ropes will not stay around for long: they will interact with each other and the remaining sheet-like structures, cascade, align, and form smaller, more sheet-like structures: this process will be studied in the next section. However, we can predict the relationship between the amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{fr}}$
and radius
$\unicode[STIX]{x1D6FF}z_{\text{fr}}$
and radius
![]() $\unicode[STIX]{x1D706}$
of the newly created flux ropes: upon inserting (5.2) into (5.5), we get
$\unicode[STIX]{x1D706}$
of the newly created flux ropes: upon inserting (5.2) into (5.5), we get
It is important to note that this is not a prediction for the scaling of any structure function or the spectrum of the disrupted turbulence (which will be worked out in the next section); rather, this is a relationship describing individual flux ropes upon their formation within an aligned structure.
Thus, provided that
![]() $\unicode[STIX]{x1D6FD}_{e}$
and
$\unicode[STIX]{x1D6FD}_{e}$
and
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
are small enough that
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
are small enough that
![]() $q_{\text{D}}>0$
before the cascade reaches
$q_{\text{D}}>0$
before the cascade reaches
![]() $\unicode[STIX]{x1D70C}_{s}$
, i.e.
$\unicode[STIX]{x1D70C}_{s}$
, i.e.
![]() $\unicode[STIX]{x1D6FD}_{e}<\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[\infty ]$
given by (4.9), there should be a strong relationship between the amplitude and radius of the structures at scales between
$\unicode[STIX]{x1D6FD}_{e}<\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}[\infty ]$
given by (4.9), there should be a strong relationship between the amplitude and radius of the structures at scales between
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[\infty ]$
, given by (4.3) and
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[\infty ]$
, given by (4.3) and
![]() $\unicode[STIX]{x1D70C}_{s}$
: indeed, the scaling (5.6) is very steep with
$\unicode[STIX]{x1D70C}_{s}$
: indeed, the scaling (5.6) is very steep with
![]() $\unicode[STIX]{x1D706}$
and the flux ropes with the largest radius
$\unicode[STIX]{x1D706}$
and the flux ropes with the largest radius
![]() $\unicode[STIX]{x1D706}_{\text{D}}[\infty ]$
also have the largest amplitude,
$\unicode[STIX]{x1D706}_{\text{D}}[\infty ]$
also have the largest amplitude,
![]() $\unicode[STIX]{x1D6FF}z_{\text{fr}}\sim \overline{\unicode[STIX]{x1D6FF}z}$
. The scaling (5.6) could in principle be tested against observations such as those reported by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016), who observed 12 ‘Alfvén vortices’ with diameters between
$\unicode[STIX]{x1D6FF}z_{\text{fr}}\sim \overline{\unicode[STIX]{x1D6FF}z}$
. The scaling (5.6) could in principle be tested against observations such as those reported by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016), who observed 12 ‘Alfvén vortices’ with diameters between
![]() $5\unicode[STIX]{x1D70C}_{i}$
and
$5\unicode[STIX]{x1D70C}_{i}$
and
![]() $17\unicode[STIX]{x1D70C}_{i}$
(as part of a sample of over 100 coherent structures of different types).
$17\unicode[STIX]{x1D70C}_{i}$
(as part of a sample of over 100 coherent structures of different types).
6 Disruption range turbulence
In a realistic situation relevant to coronal or solar-wind turbulence, the separation between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
is so small that it would be challenging to establish a robust distinction between these two scales. It is nonetheless interesting to speculate on the nature of the turbulence in the interval
$\unicode[STIX]{x1D70C}_{s}$
is so small that it would be challenging to establish a robust distinction between these two scales. It is nonetheless interesting to speculate on the nature of the turbulence in the interval
![]() $\unicode[STIX]{x1D706}_{\text{D}}\gg \unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D70C}_{s}$
in the asymptotic case where
$\unicode[STIX]{x1D706}_{\text{D}}\gg \unicode[STIX]{x1D706}\gg \unicode[STIX]{x1D70C}_{s}$
in the asymptotic case where
![]() $L_{\bot }\rightarrow \infty$
.
$L_{\bot }\rightarrow \infty$
.
As described in § 3, we expect the disruption process to convert the sheet-like structures just above
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
into flux-rope-like structures just below
$\unicode[STIX]{x1D706}_{\text{D}}$
into flux-rope-like structures just below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
. These are roughly circular in the perpendicular plane, with radius
$\unicode[STIX]{x1D706}_{\text{D}}$
. These are roughly circular in the perpendicular plane, with radius
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, but extended in the parallel direction due to critical balance. In order to treat this ‘disruption range’ properly, we would need to account for the intermittency of both sheets and flux ropes. We do not attempt such a treatment in this paper. Instead, we develop a simpler model, in which we take the sheets and flux ropes to be effectively volume filling, and the sheets to have the properties of the
$\unicode[STIX]{x1D706}_{\text{D}}$
, but extended in the parallel direction due to critical balance. In order to treat this ‘disruption range’ properly, we would need to account for the intermittency of both sheets and flux ropes. We do not attempt such a treatment in this paper. Instead, we develop a simpler model, in which we take the sheets and flux ropes to be effectively volume filling, and the sheets to have the properties of the
![]() $n=2$
structures of § 2 (since we would like to explore the scaling of the energy spectrum below
$n=2$
structures of § 2 (since we would like to explore the scaling of the energy spectrum below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
). For simplicity of notation, we will drop the ‘
$\unicode[STIX]{x1D706}_{\text{D}}$
). For simplicity of notation, we will drop the ‘
![]() $[n=2]$
’ argument of all relevant quantities. A ‘characteristic fluctuation amplitude’
$[n=2]$
’ argument of all relevant quantities. A ‘characteristic fluctuation amplitude’
![]() $\unicode[STIX]{x1D6FF}z_{1,-}$
for the turbulence just below
$\unicode[STIX]{x1D6FF}z_{1,-}$
for the turbulence just below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
may be defined by assuming that there is negligible dissipation during the disruption process, so that the energy flux stays constant across the disruption scaleFootnote
7
. Further assuming (radically) that the turbulence just below
$\unicode[STIX]{x1D706}_{\text{D}}$
may be defined by assuming that there is negligible dissipation during the disruption process, so that the energy flux stays constant across the disruption scaleFootnote
7
. Further assuming (radically) that the turbulence just below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
loses all its dynamic alignment, the scale
$\unicode[STIX]{x1D706}_{\text{D}}$
loses all its dynamic alignment, the scale
![]() $\unicode[STIX]{x1D709}$
is no longer relevant and the only perpendicular scale in the problem is
$\unicode[STIX]{x1D709}$
is no longer relevant and the only perpendicular scale in the problem is
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
:
$\unicode[STIX]{x1D706}_{\text{D}}$
:
giving
Note that this is smaller than the amplitude of the aligned turbulence at the same scale:
The definition (6.2) might appear to be in contradiction with our earlier assumption (5.5) that the flux ropes should be formed with the same amplitude as their ‘mother sheet’. Indeed, if one took (5.5), (6.2) and (6.3) together, they imply that the flux ropes created by a disrupting sheet fill only a fraction of the mother sheet’s volume, contradicting our supposition above. However, (6.2) is not meant to be the amplitude of any individual structure, but rather an effective estimate that would on average give (6.1). In this sense, there is no difference between (6.2) or (6.3) and the usual ‘twiddle’ relations in Kolmogorov-style turbulence phenomenologies relying on constant energy flux and ignoring intermittency and local imbalance: the amplitude (6.2) is an estimate that effectively absorbs within itself the filling fraction (probability of occurrence) of energetic structures that contribute to averages, as well as the (unknown) details of how precisely the nonlinear interactions within or between flux ropes (and between flux ropes and ambient turbulence) actually occur. In the case of flux ropes, it is clear that to make a connection between (5.5) and any average quantity, one would need to take into account the fact that they are clearly less volume filling than their mother sheets, have shorter lifetimes, and might mainly cascade due to interactions between different types of structures. We leapfrog these issues with the aid of the requirement (6.1) that energy flux should stay the same. This will allow us to make progress and develop a simple model in this section: (6.2) will define the ‘outer scale amplitude’ for the Alfvénic cascade below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
. Intermittency is known to be of crucial importance in Alfvénic turbulence (Chandran et al.
Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017), and so a more rigorous model incorporating intermittency should be the subject of future work.
$\unicode[STIX]{x1D706}_{\text{D}}$
. Intermittency is known to be of crucial importance in Alfvénic turbulence (Chandran et al.
Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017), and so a more rigorous model incorporating intermittency should be the subject of future work.
Following Mallet et al. (Reference Mallet, Schekochihin and Chandran2017), the turbulence just below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
should behave just like the usual Alfvénic turbulence described in § 2 (since
$\unicode[STIX]{x1D706}_{\text{D}}$
should behave just like the usual Alfvénic turbulence described in § 2 (since
![]() $\unicode[STIX]{x1D706}_{\text{D}}\gg \unicode[STIX]{x1D70C}_{s}$
): the flux ropes will interact with each other and the rest of the turbulence, causing a cascade to smaller scalesFootnote
8
. In the course of this secondary cascade, the turbulence will again start to dynamically align and form sheet-like structures, and may eventually be disrupted by the onset of reconnection at a secondary disruption scale
$\unicode[STIX]{x1D706}_{\text{D}}\gg \unicode[STIX]{x1D70C}_{s}$
): the flux ropes will interact with each other and the rest of the turbulence, causing a cascade to smaller scalesFootnote
8
. In the course of this secondary cascade, the turbulence will again start to dynamically align and form sheet-like structures, and may eventually be disrupted by the onset of reconnection at a secondary disruption scale
![]() $\unicode[STIX]{x1D706}_{\text{D},2}$
, at which the whole process repeats – provided that
$\unicode[STIX]{x1D706}_{\text{D},2}$
, at which the whole process repeats – provided that
![]() $\unicode[STIX]{x1D706}_{\text{D},2}>\unicode[STIX]{x1D70C}_{s}$
. Therefore, the turbulence between the first disruption scale
$\unicode[STIX]{x1D706}_{\text{D},2}>\unicode[STIX]{x1D70C}_{s}$
. Therefore, the turbulence between the first disruption scale
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
(which we will now rechristen
$\unicode[STIX]{x1D706}_{\text{D}}$
(which we will now rechristen
![]() $\unicode[STIX]{x1D706}_{\text{D},1}$
) and
$\unicode[STIX]{x1D706}_{\text{D},1}$
) and
![]() $\unicode[STIX]{x1D70C}_{s}$
is characterised by a sequence of disruptions, between which the turbulence realigns. We will now show that this recursive disruption process is unlikely to be fully realised, and usually terminates after only one disruption.
$\unicode[STIX]{x1D70C}_{s}$
is characterised by a sequence of disruptions, between which the turbulence realigns. We will now show that this recursive disruption process is unlikely to be fully realised, and usually terminates after only one disruption.
6.1 Recursive disruption?
The sequence of disruptions described above may be understood in terms of a recursion relation. After the
![]() $(i-1)$
st disruption, the turbulence undergoes the
$(i-1)$
st disruption, the turbulence undergoes the
![]() $i$
th ‘mini-cascade’, with ‘outer-scale’ values of the relevant quantities given by the values just below the
$i$
th ‘mini-cascade’, with ‘outer-scale’ values of the relevant quantities given by the values just below the
![]() $(i-1)$
st disruption scale
$(i-1)$
st disruption scale
![]() $\unicode[STIX]{x1D706}_{\text{D},i-1}$
:
$\unicode[STIX]{x1D706}_{\text{D},i-1}$
:
Substituting this into (4.4) and normalising by
![]() $L_{\bot }$
, we obtain the
$L_{\bot }$
, we obtain the
![]() $i$
th disruption scale
$i$
th disruption scale
Unlike in the resistive case (Mallet et al.
Reference Mallet, Schekochihin and Chandran2017), this sequence will always terminate after a finite number of disruptions, because
![]() $\unicode[STIX]{x1D70C}_{s}>d_{e}$
and so eventually
$\unicode[STIX]{x1D70C}_{s}>d_{e}$
and so eventually
![]() $\unicode[STIX]{x1D706}_{\text{D},i}<\unicode[STIX]{x1D70C}_{s}$
. The number of disruptions is given by the greatest
$\unicode[STIX]{x1D706}_{\text{D},i}<\unicode[STIX]{x1D70C}_{s}$
. The number of disruptions is given by the greatest
![]() $i=i_{\text{max}}$
for which
$i=i_{\text{max}}$
for which
It is obvious from the exponent of
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
in (6.6) that, for there to be more than one disruption,
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
in (6.6) that, for there to be more than one disruption,
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
must be unrealistically large. Namely, (6.6) may be solved for
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
must be unrealistically large. Namely, (6.6) may be solved for
![]() $i_{\text{max}}$
, showing an extremely weak dependence on
$i_{\text{max}}$
, showing an extremely weak dependence on
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
:
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
:
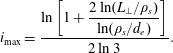 $$\begin{eqnarray}i_{\text{max}}=\frac{\ln \left[1+{\displaystyle \frac{2\ln (L_{\bot }/\unicode[STIX]{x1D70C}_{s})}{\ln (\unicode[STIX]{x1D70C}_{s}/d_{e})}}\right]}{2\ln 3}.\end{eqnarray}$$
$$\begin{eqnarray}i_{\text{max}}=\frac{\ln \left[1+{\displaystyle \frac{2\ln (L_{\bot }/\unicode[STIX]{x1D70C}_{s})}{\ln (\unicode[STIX]{x1D70C}_{s}/d_{e})}}\right]}{2\ln 3}.\end{eqnarray}$$
With
![]() $d_{e}/\unicode[STIX]{x1D70C}_{s}$
kept constant as
$d_{e}/\unicode[STIX]{x1D70C}_{s}$
kept constant as
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}\rightarrow \infty$
, the number of disruptions grows extremely slowly, so, in a moderately low-
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}\rightarrow \infty$
, the number of disruptions grows extremely slowly, so, in a moderately low-
![]() $\unicode[STIX]{x1D6FD}_{e}$
situation where
$\unicode[STIX]{x1D6FD}_{e}$
situation where
![]() $d_{e}/\unicode[STIX]{x1D70C}_{s}<1$
, it is very unlikely that more than one disruption will occur.
$d_{e}/\unicode[STIX]{x1D70C}_{s}<1$
, it is very unlikely that more than one disruption will occur.
6.2 Effective spectral index below
 $\unicode[STIX]{x1D706}_{\text{D}}$
: many disruptions
$\unicode[STIX]{x1D706}_{\text{D}}$
: many disruptions
Nevertheless, in the spirit of asymptotic fantasising, let us determine the effective spectral index in a scale range featuring many disruptions. With the substitutions (6.4), the characteristic fluctuation amplitude just below each disruption scale is [cf. (6.2)]
Therefore, the fluctuation amplitude associated with the
![]() $i$
th aligning ‘mini-cascade’ between disruption scales
$i$
th aligning ‘mini-cascade’ between disruption scales
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i-1}$
and
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i-1}$
and
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
is
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
is
The characteristic aspect ratio of the turbulence (equivalently, the inverse alignment angle) between disruptions is then
which is much smaller than the value (
![]() $\hat{\unicode[STIX]{x1D706}}^{-1/4}$
) that would have been attained without the disruptions. The ‘coarse-grained’ fluctuation amplitude calculated at the scale just above the
$\hat{\unicode[STIX]{x1D706}}^{-1/4}$
) that would have been attained without the disruptions. The ‘coarse-grained’ fluctuation amplitude calculated at the scale just above the
![]() $i$
th disruption is [cf. (6.3)]
$i$
th disruption is [cf. (6.3)]
where we have used (6.5) to obtain the second expression. Since (6.11) is larger than (6.8), our model spectrum looks like a sloping staircase, with (6.11) providing an upper envelope for the true scaling of the fluctuation amplitude (the true spectrum and structure function will not, of course, have discontinuities). Thus,
![]() $\unicode[STIX]{x1D6FF}z_{+,i}\propto \unicode[STIX]{x1D706}_{\text{D},i}$
, and so the effective scaling exponent of the fluctuation amplitudes is
$\unicode[STIX]{x1D6FF}z_{+,i}\propto \unicode[STIX]{x1D706}_{\text{D},i}$
, and so the effective scaling exponent of the fluctuation amplitudes is
![]() $\unicode[STIX]{x1D6FC}_{\text{eff}}=1$
. This implies a spectral index of
$\unicode[STIX]{x1D6FC}_{\text{eff}}=1$
. This implies a spectral index of
![]() $-1-2\unicode[STIX]{x1D6FC}_{\text{eff}}=-3$
, slightly steeper than the observed spectral index
$-1-2\unicode[STIX]{x1D6FC}_{\text{eff}}=-3$
, slightly steeper than the observed spectral index
![]() ${\approx}-2.8$
below the ion scales in strong kinetic Alfvén wave turbulence in the solar wind (Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Chen et al.
Reference Chen, Horbury, Schekochihin, Wicks, Alexandrova and Mitchell2010; Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010).
${\approx}-2.8$
below the ion scales in strong kinetic Alfvén wave turbulence in the solar wind (Alexandrova et al.
Reference Alexandrova, Saur, Lacombe, Mangeney, Mitchell, Schwartz and Robert2009; Chen et al.
Reference Chen, Horbury, Schekochihin, Wicks, Alexandrova and Mitchell2010; Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010).
Exactly the same scaling is (of course) found by observing that
![]() $\unicode[STIX]{x1D70F}_{\text{C}}\sim \unicode[STIX]{x1D6FE}_{{>}}^{-1}$
on the coarse-grained points
$\unicode[STIX]{x1D70F}_{\text{C}}\sim \unicode[STIX]{x1D6FE}_{{>}}^{-1}$
on the coarse-grained points
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
: then, constancy of energy flux through all scales implies that (cf. Boldyrev & Loureiro Reference Boldyrev and Loureiro2017)
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
: then, constancy of energy flux through all scales implies that (cf. Boldyrev & Loureiro Reference Boldyrev and Loureiro2017)
6.3 Effective spectral index below
 $\unicode[STIX]{x1D706}_{\text{D}}$
: one disruption
$\unicode[STIX]{x1D706}_{\text{D}}$
: one disruption
For realistic values of
![]() $L_{\bot }$
and
$L_{\bot }$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
, there is only one disruption, i.e.
$\unicode[STIX]{x1D70C}_{s}$
, there is only one disruption, i.e.
![]() $i_{\text{max}}=1$
. The aligning cascade below
$i_{\text{max}}=1$
. The aligning cascade below
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
then gives an amplitude at
$\unicode[STIX]{x1D706}_{\text{D}}$
then gives an amplitude at
![]() $\unicode[STIX]{x1D70C}_{s}$
of
$\unicode[STIX]{x1D70C}_{s}$
of
using (6.9). The characteristic aspect ratio of the turbulence at
![]() $\unicode[STIX]{x1D70C}_{s}$
is, using (6.10),
$\unicode[STIX]{x1D70C}_{s}$
is, using (6.10),
which is approximately unity for any realistic set of parameters. Therefore, the turbulence at the ion scale, i.e. at the largest scales in the kinetic Alfvén wave cascade, will be very different depending on the presence or absence of the disruption: namely, it will either be nearly isotropic (in the perpendicular plane), as per (6.10), or highly anisotropic (aligned) with aspect ratio
![]() $(\unicode[STIX]{x1D70C}_{s}/L_{\bot })^{-1/4}$
, respectively. In reality, there may be a mixture of both types of structures, as is suggested by the discussion in § 5.1 – so the reduction in the alignment may not be as drastic as suggested by the extreme estimate (6.14).
$(\unicode[STIX]{x1D70C}_{s}/L_{\bot })^{-1/4}$
, respectively. In reality, there may be a mixture of both types of structures, as is suggested by the discussion in § 5.1 – so the reduction in the alignment may not be as drastic as suggested by the extreme estimate (6.14).
The effective scaling of the fluctuation amplitudes between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
will be steeper than
$\unicode[STIX]{x1D70C}_{s}$
will be steeper than
![]() $\unicode[STIX]{x1D6FC}_{\text{eff}}=1$
derived in § 6.2, because the recursive disruptions are cut off by the presence of the ion scale
$\unicode[STIX]{x1D6FC}_{\text{eff}}=1$
derived in § 6.2, because the recursive disruptions are cut off by the presence of the ion scale
![]() $\unicode[STIX]{x1D70C}_{s}$
. The effective scaling in this case is given by
$\unicode[STIX]{x1D70C}_{s}$
. The effective scaling in this case is given by
This ranges between
![]() $1\leqslant \unicode[STIX]{x1D6FC}_{\text{eff}}<\infty$
, increasing the closer
$1\leqslant \unicode[STIX]{x1D6FC}_{\text{eff}}<\infty$
, increasing the closer
![]() $\unicode[STIX]{x1D70C}_{s}$
gets to
$\unicode[STIX]{x1D70C}_{s}$
gets to
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
. Thus the effective spectral index in a ‘realistic’ short range of scales between
$\unicode[STIX]{x1D706}_{\text{D}}$
. Thus the effective spectral index in a ‘realistic’ short range of scales between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
, with only one disruption, may be somewhat steeper than
$\unicode[STIX]{x1D70C}_{s}$
, with only one disruption, may be somewhat steeper than
![]() $-3$
, and may depend on
$-3$
, and may depend on
![]() $\unicode[STIX]{x1D6FD}_{e}$
(i.e. it is not universal). Here again, the caveat that disruption does not in fact occur at a single scale or in every aligned structure implies that the spectrum should not be as dramatically steepened as (6.15) suggests. A spectrum slightly steeper than
$\unicode[STIX]{x1D6FD}_{e}$
(i.e. it is not universal). Here again, the caveat that disruption does not in fact occur at a single scale or in every aligned structure implies that the spectrum should not be as dramatically steepened as (6.15) suggests. A spectrum slightly steeper than
![]() $-3$
is probably a reasonable expectation.
$-3$
is probably a reasonable expectation.
Short intervals of steep spectra are indeed sometimes observed near the ion scales in the solar wind: Sahraoui et al. (Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010) and Lion et al. (Reference Lion, Alexandrova and Zaslavsky2016) report a spectral index close to
![]() $-4$
in a small ‘transition range’ of scales near the ion gyroradius. Lion et al. (Reference Lion, Alexandrova and Zaslavsky2016) attribute this spectral index to Alfvén vortices (Alexandrova Reference Alexandrova2008) with scales a few times the ion gyroradius.
$-4$
in a small ‘transition range’ of scales near the ion gyroradius. Lion et al. (Reference Lion, Alexandrova and Zaslavsky2016) attribute this spectral index to Alfvén vortices (Alexandrova Reference Alexandrova2008) with scales a few times the ion gyroradius.
7 Discussion
Models of strong Alfvénic turbulence that incorporate dynamic alignment predict that the turbulent structures become progressively more sheet-like at smaller scales (Boldyrev Reference Boldyrev2006; Chandran et al.
Reference Chandran, Schekochihin and Mallet2015; Mallet & Schekochihin Reference Mallet and Schekochihin2017). This suggests that at some sufficiently small scale
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
, the cascade time of the structures may be slower than the time required to disrupt them via magnetic reconnection. For resistive RMHD, this scale was calculated by Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) and Loureiro & Boldyrev (Reference Loureiro and Boldyrev2017a
). In this paper, we have extended this idea to the case of a weakly collisional, low-
$\unicode[STIX]{x1D706}_{\text{D}}$
, the cascade time of the structures may be slower than the time required to disrupt them via magnetic reconnection. For resistive RMHD, this scale was calculated by Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) and Loureiro & Boldyrev (Reference Loureiro and Boldyrev2017a
). In this paper, we have extended this idea to the case of a weakly collisional, low-
![]() $\unicode[STIX]{x1D6FD}_{e}$
plasma, in which the reconnection is due to electron inertia, rather than resistivity, and two-fluid effects become important at ion scales. We find that there is again a critical scale,
$\unicode[STIX]{x1D6FD}_{e}$
plasma, in which the reconnection is due to electron inertia, rather than resistivity, and two-fluid effects become important at ion scales. We find that there is again a critical scale,
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}\sim L_{\bot }^{1/9}(d_{e}\unicode[STIX]{x1D70C}_{s})^{4/9}$
, below which the sheet-like structures are destroyed by reconnection. For sufficiently low electron beta, and sufficiently large-scale separation between the outer scale
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}\sim L_{\bot }^{1/9}(d_{e}\unicode[STIX]{x1D70C}_{s})^{4/9}$
, below which the sheet-like structures are destroyed by reconnection. For sufficiently low electron beta, and sufficiently large-scale separation between the outer scale
![]() $L_{\bot }$
and the ion sound scale
$L_{\bot }$
and the ion sound scale
![]() $\unicode[STIX]{x1D70C}_{s}$
, this scale lies in the inertial range:
$\unicode[STIX]{x1D70C}_{s}$
, this scale lies in the inertial range:
![]() $\unicode[STIX]{x1D706}_{\text{D}}>\unicode[STIX]{x1D70C}_{s}$
. The break in the energy spectrum of turbulence in a low-
$\unicode[STIX]{x1D706}_{\text{D}}>\unicode[STIX]{x1D70C}_{s}$
. The break in the energy spectrum of turbulence in a low-
![]() $\unicode[STIX]{x1D6FD}$
collisionless plasma can thus occur at a larger scale than expected based on linear physics of wave modes – it does indeed do so in the solar wind (Bourouaine et al.
Reference Bourouaine, Alexandrova, Marsch and Maksimovic2012; Chen et al.
Reference Chen, Leung, Boldyrev, Maruca and Bale2014), although the observed scaling of the break scale with
$\unicode[STIX]{x1D6FD}$
collisionless plasma can thus occur at a larger scale than expected based on linear physics of wave modes – it does indeed do so in the solar wind (Bourouaine et al.
Reference Bourouaine, Alexandrova, Marsch and Maksimovic2012; Chen et al.
Reference Chen, Leung, Boldyrev, Maruca and Bale2014), although the observed scaling of the break scale with
![]() $\unicode[STIX]{x1D6FD}_{i}$
appears to be stronger than we are able to predict here, unless there is some systematic correlation of the electron–ion temperature ratio with
$\unicode[STIX]{x1D6FD}_{i}$
appears to be stronger than we are able to predict here, unless there is some systematic correlation of the electron–ion temperature ratio with
![]() $\unicode[STIX]{x1D6FD}_{i}$
.
$\unicode[STIX]{x1D6FD}_{i}$
.
We have argued that between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
, the spectral index of the turbulent fluctuations should be steeper than
$\unicode[STIX]{x1D70C}_{s}$
, the spectral index of the turbulent fluctuations should be steeper than
![]() $-3$
. A steep ‘transition range’ around the ion scale is indeed sometimes observed in the real solar wind (Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010). This has been attributed to the presence of Alfvén vortices (Alexandrova Reference Alexandrova2008; Lion et al.
Reference Lion, Alexandrova and Zaslavsky2016). These may be similar to the flux-rope-like structures that we envision in this paper to be the product of the disruption of the aligned cascade, and so disruption via tearing may be a physical reason for the presence of Alfvén vortices at ion scales in the solar wind. We predict that such structures should become very unlikely above a certain
$-3$
. A steep ‘transition range’ around the ion scale is indeed sometimes observed in the real solar wind (Sahraoui et al.
Reference Sahraoui, Goldstein, Belmont, Canu and Rezeau2010). This has been attributed to the presence of Alfvén vortices (Alexandrova Reference Alexandrova2008; Lion et al.
Reference Lion, Alexandrova and Zaslavsky2016). These may be similar to the flux-rope-like structures that we envision in this paper to be the product of the disruption of the aligned cascade, and so disruption via tearing may be a physical reason for the presence of Alfvén vortices at ion scales in the solar wind. We predict that such structures should become very unlikely above a certain
![]() $\unicode[STIX]{x1D6FD}_{e}$
[given by (4.9)], and that as
$\unicode[STIX]{x1D6FD}_{e}$
[given by (4.9)], and that as
![]() $\unicode[STIX]{x1D6FD}_{e}$
decreases, the proportion of the volume at the ion scale filled with aligned, undisrupted structures decreases, as does the amount of energy contained in them (§ 5.1). We also propose the relationship (5.6) between the amplitude and radius of the individual flux-rope structures. This could potentially be tested by solar-wind observations of the kind performed by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016).
$\unicode[STIX]{x1D6FD}_{e}$
decreases, the proportion of the volume at the ion scale filled with aligned, undisrupted structures decreases, as does the amount of energy contained in them (§ 5.1). We also propose the relationship (5.6) between the amplitude and radius of the individual flux-rope structures. This could potentially be tested by solar-wind observations of the kind performed by Perrone et al. (Reference Perrone, Alexandrova, Mangeney, Maksimovic, Lacombe, Rakoto, Kasper and Jovanovic2016).
For the Alfvénic turbulence to be disrupted by reconnection, we need
![]() $\unicode[STIX]{x1D706}_{\text{D}}>\unicode[STIX]{x1D70C}_{s}$
. This inequality translates into a requirement that the electron plasma beta must be less than some critical value
$\unicode[STIX]{x1D706}_{\text{D}}>\unicode[STIX]{x1D70C}_{s}$
. This inequality translates into a requirement that the electron plasma beta must be less than some critical value
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, given by (4.7), which depends on the ratio
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, given by (4.7), which depends on the ratio
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
of the outer scale to the ion scale and on the amplitude of the structures being considered. In the solar wind,
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
of the outer scale to the ion scale and on the amplitude of the structures being considered. In the solar wind,
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}\approx 10^{3}$
, and we find that for fluctuations of moderate amplitude (ones that dominate the energy spectrum),
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}\approx 10^{3}$
, and we find that for fluctuations of moderate amplitude (ones that dominate the energy spectrum),
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}\sim 0.01$
, while for the most intense (but rare and intermittent) fluctuations,
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}\sim 0.01$
, while for the most intense (but rare and intermittent) fluctuations,
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}\sim 1$
. Thus, we expect only the most intense structures to be disrupted in the solar wind at 1 AU, where
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}\sim 1$
. Thus, we expect only the most intense structures to be disrupted in the solar wind at 1 AU, where
![]() $\unicode[STIX]{x1D6FD}_{e}\sim 1$
. Closer to the sun,
$\unicode[STIX]{x1D6FD}_{e}\sim 1$
. Closer to the sun,
![]() $\unicode[STIX]{x1D6FD}_{e}$
may be lower (Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011), and the disruption process becomes more effective.
$\unicode[STIX]{x1D6FD}_{e}$
may be lower (Chandran et al.
Reference Chandran, Dennis, Quataert and Bale2011), and the disruption process becomes more effective.
The turbulence at the ion scale is significantly different depending on whether disruption due to the onset of reconnection can occur or not. Above
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, sheet-like Alfvénic structures with a large aspect ratio will reach the ion scale without disruption. Below
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, sheet-like Alfvénic structures with a large aspect ratio will reach the ion scale without disruption. Below
![]() $\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, the disruption should occur, and turbulence at the ion scale should become much less anisotropic (less aligned) in the perpendicular plane (see § 6.3). Thus, the nature of the turbulence at the ion scale, which provides the starting point for the sub-ion-scale kinetic Alfvén wave turbulence, depends crucially on whether the disruption process occurs.
$\unicode[STIX]{x1D6FD}_{e}^{\text{crit}}$
, the disruption should occur, and turbulence at the ion scale should become much less anisotropic (less aligned) in the perpendicular plane (see § 6.3). Thus, the nature of the turbulence at the ion scale, which provides the starting point for the sub-ion-scale kinetic Alfvén wave turbulence, depends crucially on whether the disruption process occurs.
Acknowledgements
We thank N. Loureiro and O. Alexandrova for useful conversations. The work of A.M. was supported by NSF grant AGS-1624501. B.D.G.C. was supported by NASA grants NNX15AI80G, NNX16AG81G, and NNX17AI18G, and NSF grant PHY-1500041. The work of A.A.S. was supported in part by grants from UK STFC and EPSRC.
Appendix A. Semicollisional disruption
Here, we will replicate some of the calculations done in the main text, but this time for a low-
![]() $\unicode[STIX]{x1D6FD}$
‘semicollisional’, large-guide-field regime where the width of the diffusive layer
$\unicode[STIX]{x1D6FD}$
‘semicollisional’, large-guide-field regime where the width of the diffusive layer
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}$
is smaller than
$\unicode[STIX]{x1D6FF}_{\text{in}}$
is smaller than
![]() $\unicode[STIX]{x1D70C}_{s}$
, but is controlled by resistivity rather than by electron inertia. For the turbulence, this means that the ion scale is greater than the resistive scale that would have provided the dissipative cutoff in fully collisional MHD,
$\unicode[STIX]{x1D70C}_{s}$
, but is controlled by resistivity rather than by electron inertia. For the turbulence, this means that the ion scale is greater than the resistive scale that would have provided the dissipative cutoff in fully collisional MHD,
but the electron–ion collision rate is nevertheless much larger than the nonlinear cascade rate of the fluctuations, or the growth rate of the tearing mode,
This means that the flux conservation is broken by Ohmic resistivity
![]() $\unicode[STIX]{x1D702}=\unicode[STIX]{x1D708}_{ei}d_{e}^{2}$
rather than by electron inertia, but the two-fluid effects are still important. This situation is relevant to many laboratory plasmas, for example TREX (Forest et al.
Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015) and FLARE (Ji et al.
Reference Ji, Bhattacharjee, Prager, Daughton, Bale, Carter, Crocker, Drake, Egedal and Sarff2014), as well as in hybrid-kinetic simulations that do not model the electron inertia (e.g. Parashar et al.
Reference Parashar, Shay, Cassak and Matthaeus2009; Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017).
$\unicode[STIX]{x1D702}=\unicode[STIX]{x1D708}_{ei}d_{e}^{2}$
rather than by electron inertia, but the two-fluid effects are still important. This situation is relevant to many laboratory plasmas, for example TREX (Forest et al.
Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015) and FLARE (Ji et al.
Reference Ji, Bhattacharjee, Prager, Daughton, Bale, Carter, Crocker, Drake, Egedal and Sarff2014), as well as in hybrid-kinetic simulations that do not model the electron inertia (e.g. Parashar et al.
Reference Parashar, Shay, Cassak and Matthaeus2009; Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Cerri & Califano Reference Cerri and Califano2017; Cerri et al.
Reference Cerri, Franci, Califano, Landi and Hellinger2017).
A.1 Semicollisional tearing mode
Growth rates of the tearing mode in this regime are reviewed in appendix B.5 of Zocco & Schekochihin (Reference Zocco and Schekochihin2011). We will assume that the turbulent structures are still given by our RMHD turbulence model summarised in § 2; namely, they have a width
![]() $\unicode[STIX]{x1D706}$
and length
$\unicode[STIX]{x1D706}$
and length
![]() $\unicode[STIX]{x1D709}$
in the perpendicular plane, and a perturbed-magnetic-field reversal
$\unicode[STIX]{x1D709}$
in the perpendicular plane, and a perturbed-magnetic-field reversal
![]() $\unicode[STIX]{x1D6FF}b\sim \unicode[STIX]{x1D6FF}z$
across
$\unicode[STIX]{x1D6FF}b\sim \unicode[STIX]{x1D6FF}z$
across
![]() $\unicode[STIX]{x1D706}$
. The tearing mode in this regime, like its collisionless cousin in § 3, involves three-scale physics: the (unstable) ‘equilibrium’ at the scale of the turbulent structure
$\unicode[STIX]{x1D706}$
. The tearing mode in this regime, like its collisionless cousin in § 3, involves three-scale physics: the (unstable) ‘equilibrium’ at the scale of the turbulent structure
![]() $\unicode[STIX]{x1D706}$
, two-fluid effects at around the ion sound scale
$\unicode[STIX]{x1D706}$
, two-fluid effects at around the ion sound scale
![]() $\unicode[STIX]{x1D70C}_{s}$
, and flux unfreezing in an inner layer of width
$\unicode[STIX]{x1D70C}_{s}$
, and flux unfreezing in an inner layer of width
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}\ll \unicode[STIX]{x1D70C}_{s}$
, controlled by resistivity.
$\unicode[STIX]{x1D6FF}_{\text{in}}\ll \unicode[STIX]{x1D70C}_{s}$
, controlled by resistivity.
We will again consider the long-wavelength limit,
![]() $k\unicode[STIX]{x1D706}\ll 1$
, and assume (3.1). For
$k\unicode[STIX]{x1D706}\ll 1$
, and assume (3.1). For
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\ll 1$
, the linear growth rate and the inner layer’s width are
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\ll 1$
, the linear growth rate and the inner layer’s width are
where
![]() $S_{\unicode[STIX]{x1D706}}\doteq \unicode[STIX]{x1D6FF}z\unicode[STIX]{x1D706}/\unicode[STIX]{x1D702}$
is the Lundquist number based on scale
$S_{\unicode[STIX]{x1D706}}\doteq \unicode[STIX]{x1D6FF}z\unicode[STIX]{x1D706}/\unicode[STIX]{x1D702}$
is the Lundquist number based on scale
![]() $\unicode[STIX]{x1D706}$
. Note that, as in the collisionless case,
$\unicode[STIX]{x1D706}$
. Note that, as in the collisionless case,
![]() $\unicode[STIX]{x1D6FE}_{{>}}$
is independent of
$\unicode[STIX]{x1D6FE}_{{>}}$
is independent of
![]() $k$
. For
$k$
. For
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$
,
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim 1$
,
The transitional wavenumber
![]() $k_{\text{tr}}$
between these two regimes may be found by balancing the two expressions for the growth rate, giving
$k_{\text{tr}}$
between these two regimes may be found by balancing the two expressions for the growth rate, giving
For all
![]() $k>k_{\text{tr}}$
, the growth rate is given by
$k>k_{\text{tr}}$
, the growth rate is given by
![]() $\unicode[STIX]{x1D6FE}_{{>}}$
, so there is always a mode with the maximum growth rate that has a short enough wavelength to fit into the sheet.
$\unicode[STIX]{x1D6FE}_{{>}}$
, so there is always a mode with the maximum growth rate that has a short enough wavelength to fit into the sheet.
The linear stage of tearing ends when the width of the islands reaches
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}$
. This is largest for
$\unicode[STIX]{x1D6FF}_{\text{in}}$
. This is largest for
![]() $k<k_{\text{tr}}$
, so, at the end of the linear stage, the largest islands are again produced by the mode with
$k<k_{\text{tr}}$
, so, at the end of the linear stage, the largest islands are again produced by the mode with
![]() $k\sim k_{\text{tr}}$
, similarly to the collisionless case. We will, therefore, again assume that this mode dominates the nonlinear dynamics. We will also again assume that the
$k\sim k_{\text{tr}}$
, similarly to the collisionless case. We will, therefore, again assume that this mode dominates the nonlinear dynamics. We will also again assume that the
![]() $X$
-points between the islands collapse on a time scale at least as short as the linear stage, and that the islands circularise forming a set of flux ropes. Similarly to the collisionless case, if they do so at constant area, their width is
$X$
-points between the islands collapse on a time scale at least as short as the linear stage, and that the islands circularise forming a set of flux ropes. Similarly to the collisionless case, if they do so at constant area, their width is
Since we are assuming that the circularisation is at least as fast as the linear stage, we can again estimate the disruption time using the linear growth rate (A 3),
A.2 Disruption scale
Disruption of an aligned structure will occur if
Therefore, the aligned structures are disrupted for
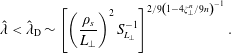 $$\begin{eqnarray}\hat{\unicode[STIX]{x1D706}}<\hat{\unicode[STIX]{x1D706}}_{\text{D}}\sim \left[\left(\frac{\unicode[STIX]{x1D70C}_{s}}{L_{\bot }}\right)^{2}S_{L_{\bot }}^{-1}\right]^{2/9\left(1-4\unicode[STIX]{x1D701}_{\bot }^{n}/9n\right)^{-1}}.\end{eqnarray}$$
$$\begin{eqnarray}\hat{\unicode[STIX]{x1D706}}<\hat{\unicode[STIX]{x1D706}}_{\text{D}}\sim \left[\left(\frac{\unicode[STIX]{x1D70C}_{s}}{L_{\bot }}\right)^{2}S_{L_{\bot }}^{-1}\right]^{2/9\left(1-4\unicode[STIX]{x1D701}_{\bot }^{n}/9n\right)^{-1}}.\end{eqnarray}$$
For the
![]() $n=2$
structures, this gives
$n=2$
structures, this gives
while for the most intense structures (
![]() $n=\infty$
),
$n=\infty$
),
The disruption scale is larger than
![]() $\unicode[STIX]{x1D70C}_{s}$
when
$\unicode[STIX]{x1D70C}_{s}$
when
![]() $S_{L_{\bot }}$
is below an
$S_{L_{\bot }}$
is below an
![]() $n$
-dependent critical value:
$n$
-dependent critical value:
For the
![]() $n=2$
structures,
$n=2$
structures,
and for the
![]() $n=\infty$
structures,
$n=\infty$
structures,
Thus, the disruption becomes progressively more important to the aligned Alfvénic turbulence above the ion scale as
![]() $S_{L_{\bot }}$
decreases – until
$S_{L_{\bot }}$
decreases – until
![]() $S_{L_{\bot }}^{-3/4}\gtrsim \unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, at which point the semicollisional tearing mode scalings are no longer valid and the fully resistive regime studied in Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) is reached.
$S_{L_{\bot }}^{-3/4}\gtrsim \unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, at which point the semicollisional tearing mode scalings are no longer valid and the fully resistive regime studied in Mallet et al. (Reference Mallet, Schekochihin and Chandran2017) is reached.
Note that, from (A 10),
This can be compared with attainable values of
![]() $S_{L_{\bot }}$
and
$S_{L_{\bot }}$
and
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
in laboratory experiments: for example, according to Forest et al. (Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015), the TREX experiment is able to access
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
in laboratory experiments: for example, according to Forest et al. (Reference Forest, Flanagan, Brookhart, Clark, Cooper, Dsangles, Egedal, Endrizzi, Khalzov and Li2015), the TREX experiment is able to access
![]() $10^{3}\lesssim S_{L_{\bot }}\lesssim 10^{5}$
and
$10^{3}\lesssim S_{L_{\bot }}\lesssim 10^{5}$
and
![]() $1\lesssim L_{\bot }/\unicode[STIX]{x1D70C}_{s}\lesssim 10^{2}$
. This results in values of the disruption scale in the interval
$1\lesssim L_{\bot }/\unicode[STIX]{x1D70C}_{s}\lesssim 10^{2}$
. This results in values of the disruption scale in the interval
and so it is at least plausible that the disruption of Alfvénic turbulence by semicollisional tearing could be observed in such an experiment.
A.3 Amplitude of flux ropes
Instead of characterising the structures by
![]() $n$
, we can, similarly to what we did with the collisionless case in § 5, return to (2.2) and treat the amplitude of a fluctuation as a random variable. Via an analogous derivation, for disruption to occur, we must have
$n$
, we can, similarly to what we did with the collisionless case in § 5, return to (2.2) and treat the amplitude of a fluctuation as a random variable. Via an analogous derivation, for disruption to occur, we must have
which is satisfied for
One may use this and (2.3) to calculate the semicollisional versions of the filling fraction of aligned structures,
![]() $f_{0}$
, and the remaining fraction of their energy,
$f_{0}$
, and the remaining fraction of their energy,
![]() $f_{2}$
[§ 5.1, (5.3) and (5.4), respectively], and show that as
$f_{2}$
[§ 5.1, (5.3) and (5.4), respectively], and show that as
![]() $S_{L_{\bot }}$
decreases, these both become smaller.
$S_{L_{\bot }}$
decreases, these both become smaller.
If we again assume that the newly created flux ropes have the same amplitude as their mother sheets [see (5.5)], then, using (A 18), we obtain a relationship between
![]() $\unicode[STIX]{x1D6FF}z_{\text{fr}}$
and
$\unicode[STIX]{x1D6FF}z_{\text{fr}}$
and
![]() $\unicode[STIX]{x1D706}$
of the flux ropes just after they are created:
$\unicode[STIX]{x1D706}$
of the flux ropes just after they are created:
This relationship between the radii and amplitudes of individual flux ropes produced by the disruption of turbulent structures could in principle be tested in laboratory plasma devices, or in numerical simulations. Note that, as in § 5.2, the largest flux ropes are produced with radius
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D}}[n=\infty ]$
and have amplitude
$\hat{\unicode[STIX]{x1D706}}_{\text{D}}[n=\infty ]$
and have amplitude
![]() $\unicode[STIX]{x1D6FF}z_{\text{fr}}\sim \overline{\unicode[STIX]{x1D6FF}z}$
.
$\unicode[STIX]{x1D6FF}z_{\text{fr}}\sim \overline{\unicode[STIX]{x1D6FF}z}$
.
A.4 Recursive disruption?
Similarly to the collisionless case (§ 6), the flux-rope-like fluctuations just below the disruption scale should seed a new Alfvénic cascade to smaller scales, aligning, and potentially disrupting again, and so on recursively until the ion scale
![]() $\unicode[STIX]{x1D70C}_{s}$
is reached. Let us again focus on
$\unicode[STIX]{x1D70C}_{s}$
is reached. Let us again focus on
![]() $n=2$
, i.e. on the fluctuations that determine the scaling of the energy spectrum. Again, (6.2) and (6.4) describe the
$n=2$
, i.e. on the fluctuations that determine the scaling of the energy spectrum. Again, (6.2) and (6.4) describe the
![]() $i$
th ‘mini-cascade’. The recursive relation between successive disruption scales is, analogously to (6.5):
$i$
th ‘mini-cascade’. The recursive relation between successive disruption scales is, analogously to (6.5):
This is valid for all
![]() $i$
for which
$i$
for which
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i}>\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, giving a condition for the
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i}>\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
, giving a condition for the
![]() $i$
th disruption to be realised:
$i$
th disruption to be realised:
This inequality is always violated for
 $$\begin{eqnarray}i_{\text{max}}\sim \frac{\ln \left(1+{\displaystyle \frac{5\ln (L_{\bot }/\unicode[STIX]{x1D70C}_{s})}{2\ln (S_{L_{\bot }}^{3/4}\unicode[STIX]{x1D70C}_{s}/L_{\bot })}}\right)}{\ln 6}<\infty ,\end{eqnarray}$$
$$\begin{eqnarray}i_{\text{max}}\sim \frac{\ln \left(1+{\displaystyle \frac{5\ln (L_{\bot }/\unicode[STIX]{x1D70C}_{s})}{2\ln (S_{L_{\bot }}^{3/4}\unicode[STIX]{x1D70C}_{s}/L_{\bot })}}\right)}{\ln 6}<\infty ,\end{eqnarray}$$
unless
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }<S_{L_{\bot }}^{-3/4}$
, at which point the semicollisional scalings are no longer valid and the system is in the fully resistive RMHD regime studied in Mallet et al. (Reference Mallet, Schekochihin and Chandran2017). We again see that for there to be more than one disruption above
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }<S_{L_{\bot }}^{-3/4}$
, at which point the semicollisional scalings are no longer valid and the system is in the fully resistive RMHD regime studied in Mallet et al. (Reference Mallet, Schekochihin and Chandran2017). We again see that for there to be more than one disruption above
![]() $\unicode[STIX]{x1D70C}_{s}$
,
$\unicode[STIX]{x1D70C}_{s}$
,
![]() $L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
must be unrealistically large. Thus, the semicollisional regime, like the collisionless regime, is always characterised by a limited number of disruptions – usually a single disruption, for realistic parameters.
$L_{\bot }/\unicode[STIX]{x1D70C}_{s}$
must be unrealistically large. Thus, the semicollisional regime, like the collisionless regime, is always characterised by a limited number of disruptions – usually a single disruption, for realistic parameters.
A.5 Effective spectral index below
 $\unicode[STIX]{x1D706}_{\text{D}}$
$\unicode[STIX]{x1D706}_{\text{D}}$
Suppose, despite the arguments in the previous section as to the real-world irrelevance of this situation, that the range of scales between
![]() $\unicode[STIX]{x1D706}_{\text{D}}$
and
$\unicode[STIX]{x1D706}_{\text{D}}$
and
![]() $\unicode[STIX]{x1D70C}_{s}$
is asymptotically broad, and there are a large number of disruptions,
$\unicode[STIX]{x1D70C}_{s}$
is asymptotically broad, and there are a large number of disruptions,
![]() $i_{\text{max}}\gg 1$
(and also the semicollisional regime remains operative, i.e.
$i_{\text{max}}\gg 1$
(and also the semicollisional regime remains operative, i.e.
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }>S_{L_{\bot }}^{-3/4}$
). Using (6.4), the turbulent amplitude just below each disruption is again (6.8). Between successive disruption scales, the aligning cascade causes the turbulent amplitude to follow (6.9), and the aspect ratio of structures is given by (6.10), but now with the disruption scales
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }>S_{L_{\bot }}^{-3/4}$
). Using (6.4), the turbulent amplitude just below each disruption is again (6.8). Between successive disruption scales, the aligning cascade causes the turbulent amplitude to follow (6.9), and the aspect ratio of structures is given by (6.10), but now with the disruption scales
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
given by (A 20). Again, the aspect ratio of the structures is greatly reduced by the disruption. The ‘coarse-grained’ amplitudes calculated at the scales just above the
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
given by (A 20). Again, the aspect ratio of the structures is greatly reduced by the disruption. The ‘coarse-grained’ amplitudes calculated at the scales just above the
![]() $i$
th disruption is [cf. (6.9)],
$i$
th disruption is [cf. (6.9)],
Thus, in the semicollisional case, the effective scaling exponent of the fluctuation amplitude is
![]() $\unicode[STIX]{x1D6FC}_{\text{eff}}=3/4$
, implying a spectral index of
$\unicode[STIX]{x1D6FC}_{\text{eff}}=3/4$
, implying a spectral index of
![]() $-2.5$
. Exactly the same scaling is obtained by noticing that on the coarse-grained points
$-2.5$
. Exactly the same scaling is obtained by noticing that on the coarse-grained points
![]() $\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
, the cascade time is just set by the linear growth rate of the tearing mode (A 3),
$\hat{\unicode[STIX]{x1D706}}_{\text{D},i}$
, the cascade time is just set by the linear growth rate of the tearing mode (A 3),
![]() $\unicode[STIX]{x1D70F}_{\text{C}}\sim \unicode[STIX]{x1D6FE}_{{>}}^{-1}$
and requiring that
$\unicode[STIX]{x1D70F}_{\text{C}}\sim \unicode[STIX]{x1D6FE}_{{>}}^{-1}$
and requiring that
![]() $\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D6FF}z^{2}/\unicode[STIX]{x1D70F}_{\text{C}}\sim \text{const.}$
[cf. (6.12)].
$\unicode[STIX]{x1D716}\sim \unicode[STIX]{x1D6FF}z^{2}/\unicode[STIX]{x1D70F}_{\text{C}}\sim \text{const.}$
[cf. (6.12)].
For realistic values of
![]() $\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
and
$\unicode[STIX]{x1D70C}_{s}/L_{\bot }$
and
![]() $S_{L_{\bot }}$
, there will be at most a single disruption before
$S_{L_{\bot }}$
, there will be at most a single disruption before
![]() $\unicode[STIX]{x1D70C}_{s}$
. Essentially an identical argument to the one given in § 6.3 implies that, due to the cutoff at
$\unicode[STIX]{x1D70C}_{s}$
. Essentially an identical argument to the one given in § 6.3 implies that, due to the cutoff at
![]() $\unicode[STIX]{x1D70C}_{s}$
, the scaling of the fluctuation amplitudes may be non-universal, somewhat steeper than (A 23), and depend on the values of the physical parameters. As in the collisionless case, the presence of the disruption causes the structures at the ion scale to be much less anisotropic within the perpendicular plane than they would have been had reconnection not interfered.
$\unicode[STIX]{x1D70C}_{s}$
, the scaling of the fluctuation amplitudes may be non-universal, somewhat steeper than (A 23), and depend on the values of the physical parameters. As in the collisionless case, the presence of the disruption causes the structures at the ion scale to be much less anisotropic within the perpendicular plane than they would have been had reconnection not interfered.