Article contents
The dependence of open cylindrical magnetoactive p-Ge and p-Si plasma waveguide mode cutoff frequencies on hole concentrations
Published online by Cambridge University Press: 01 February 2009
Abstract
In this article we give the solution of Maxwell's equations for the open circular cylindrical magnetoactive semiconductor plasma (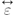 -gyrotropy) waveguides. We describe the method that allowed us to arrive at a dispersion equation for the electrodynamical analyses of open circular cylindrical plasma (OCCP) waveguides. We numerically investigate the main and two higher modes' dispersion characteristics of p-Ge and p-Si waveguides placed in an external constant longitudinal magnetic field at several concentrations of two component hole charge carriers. We analyse the cutoff frequency and other electrodynamical characteristics of helicon modes with the left-handed (e+iϕ) circular polarization. We discover that the cutoff frequencies of the main mode and the working frequency range of OCCP p-Ge and p-Si waveguides are moving continuously towards the direction of higher frequencies when the hole concentration is increasing. We determine that the central frequency of the p-Si plasma waveguide is higher and its broadbandwidth is larger compared with the analogical p-Ge waveguide. We also numerically investigate the helicon mode cutoff frequencies of the infinitive p-Ge and p-Si plasma at several concentrations of two component hole charge carriers. We compare the cutoff frequencies of the helicon modes propagating in the infinite plasma and in the OCCP waveguides.
-gyrotropy) waveguides. We describe the method that allowed us to arrive at a dispersion equation for the electrodynamical analyses of open circular cylindrical plasma (OCCP) waveguides. We numerically investigate the main and two higher modes' dispersion characteristics of p-Ge and p-Si waveguides placed in an external constant longitudinal magnetic field at several concentrations of two component hole charge carriers. We analyse the cutoff frequency and other electrodynamical characteristics of helicon modes with the left-handed (e+iϕ) circular polarization. We discover that the cutoff frequencies of the main mode and the working frequency range of OCCP p-Ge and p-Si waveguides are moving continuously towards the direction of higher frequencies when the hole concentration is increasing. We determine that the central frequency of the p-Si plasma waveguide is higher and its broadbandwidth is larger compared with the analogical p-Ge waveguide. We also numerically investigate the helicon mode cutoff frequencies of the infinitive p-Ge and p-Si plasma at several concentrations of two component hole charge carriers. We compare the cutoff frequencies of the helicon modes propagating in the infinite plasma and in the OCCP waveguides.
- Type
- Papers
- Information
- Copyright
- Copyright © Cambridge University Press 2008
References
- 11
- Cited by


