Hostname: page-component-586b7cd67f-t8hqh Total loading time: 0 Render date: 2024-11-27T19:24:17.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Density functional theory for collisionless plasmas – equivalence of fluid and kinetic approaches

Part of: The Many Facets of the Vlasov Equation

Published online by Cambridge University Press:  13 April 2020

Giovanni Manfredi Open the ORCID record for Giovanni Manfredi [Opens in a new window]
Giovanni Manfredi*
Affiliation:
Université de Strasbourg, CNRS, Institut de Physique et Chimie des Matériaux de Strasbourg, UMR 7504, F-67000Strasbourg, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Density functional theory (DFT) is a powerful theoretical tool widely used in such diverse fields as computational condensed-matter physics, atomic physics and quantum chemistry. DFT establishes that a system of 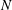$N$ interacting electrons can be described uniquely by its single-particle density 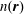$n(\boldsymbol{r})$, instead of the 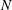$N$-body wave function, yielding an enormous gain in terms of computational speed and memory storage space. Here, we use time-dependent DFT to show that a classical collisionless plasma can always, in principle, be described by a set of fluid equations for the single-particle density and current. The results of DFT guarantee that an exact closure relation, fully reproducing the Vlasov dynamics, necessarily exists, although it may be complicated (non-local in space and time, for instance) and difficult to obtain in practice. This goes against the common wisdom in plasma physics that the Vlasov and fluid descriptions are mutually incompatible, with the latter inevitably missing some ‘purely kinetic’ effects.

Keywords

plasma dynamicssolid state plasma
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 2 , April 2020 , 825860201
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertrand, P. & Feix, M. 1968 Non linear electron plasma oscillation: the water bag model. Phys. Lett. A 28 (1), 68–69.CrossRefGoogle Scholar
Dhara, A. K. & Ghosh, S. K. 1987 Density-functional theory for time-dependent systems. Phys. Rev. A 35, 442–444.CrossRefGoogle ScholarPubMed
Feix, M. R. & Bertrand, P. 2005 A universal model: the Vlasov equation. Transp. Theory Stat. Phys. 34 (1–2), 7–62.CrossRefGoogle Scholar
Fermi, E. 1927 Un metodo statistico per la determinazione di alcune proprietà dell’atomo. Rend. Acad. Naz. Lincei 6, 602–607.Google Scholar
Hammett, G. W., Dorland, W. & Perkins, F. W. 1992 Fluid models of phase mixing, Landau damping, and nonlinear gyrokinetic dynamics. Phys. Fluids B 4 (7), 2052–2061.CrossRefGoogle Scholar
Hammett, G. W. & Perkins, F. W. 1990 Fluid moment models for Landau damping with application to the ion-temperature-gradient instability. Phys. Rev. Lett. 64, 3019–3022.CrossRefGoogle ScholarPubMed
Hohenberg, P. & Kohn, W. 1964 Inhomogeneous electron gas. Phys. Rev. E 136, B864–B871.CrossRefGoogle Scholar
Hunana, P., Zank, G. P., Laurenza, M., Tenerani, A., Webb, G. M., Goldstein, M. L., Velli, M. & Adhikari, L. 2018 New closures for more precise modeling of Landau damping in the fluid framework. Phys. Rev. Lett. 121, 135101.CrossRefGoogle ScholarPubMed
Kohn, W. & Sham, L. J. 1965 Self-consistent equations including exchange and correlation effects. Phys. Rev. E 140 (4A), A1133–A1138.CrossRefGoogle Scholar
van Leeuwen, R. 1999 Mapping from densities to potentials in time-dependent density-functional theory. Phys. Rev. Lett. 82, 3863–3866.CrossRefGoogle Scholar
Magyar, R. J., Shulenburger, L. & Baczewski, A. D. 2016 Stopping of deuterium in warm dense deuterium from ehrenfest time-dependent density functional theory. Contrib. Plasma Phys. 56 (5), 459–466.CrossRefGoogle Scholar
Marques, M. & Gross, E. 2004 Time-dependent density functional theory. Annu. Rev. Phys. Chem. 55 (1), 427–455.CrossRefGoogle ScholarPubMed
Michta, D., Graziani, F. & Bonitz, M. 2015 Quantum hydrodynamics for plasmas – a Thomas–Fermi theory perspective. Contrib. Plasma Phys. 55 (6), 437–443.CrossRefGoogle Scholar
Moldabekov, Z. A., Bonitz, M. & Ramazanov, T. S. 2018 Theoretical foundations of quantum hydrodynamics for plasmas. Phys. Plasmas 25 (3), 031903.CrossRefGoogle Scholar
Perdew, J. P. 1992 Generalized gradient approximation for the fermion kinetic energy as a functional of the density. Phys. Lett. A 165 (1), 79–82.CrossRefGoogle Scholar
Runge, E. & Gross, E. K. U. 1984 Density functional theory for time dependent systems. Phys. Rev. Lett. 52 (12), 997–1000.CrossRefGoogle Scholar
Thomas, L. H. 1927 The calculation of atomic fields. Math. Proc. Camb. Phil. Soc. 23 (5), 542–548.CrossRefGoogle Scholar
Ullrich, C. A. 2014 Time-dependent density-functional theory: features and challenges, with a special view on matter under extreme conditions. In Frontiers and Challenges in Warm Dense Matter (ed. Graziani, F., Desjarlais, M. P., Redmer, R. & Trickey, S. B.), pp. 1–23. Springer International Publishing.Google Scholar
Vignale, G. 2004 Mapping from current densities to vector potentials in time-dependent current density functional theory. Phys. Rev. B 70, 201102.CrossRefGoogle Scholar
Vignale, G. & Kohn, W. 1996 Current-dependent exchange-correlation potential for dynamical linear response theory. Phys. Rev. Lett. 77, 2037–2040.CrossRefGoogle ScholarPubMed
Vignale, G., Ullrich, C. A. & Conti, S. 1997 Time-dependent density functional theory beyond the adiabatic local density approximation. Phys. Rev. Lett. 79, 4878–4881.CrossRefGoogle Scholar