Article contents
Continuous-in-time approach to flow shear in a linearly implicit local $\delta f$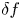 gyrokinetic code
gyrokinetic code
Published online by Cambridge University Press: 04 May 2021
Abstract
A new algorithm for toroidal flow shear in a linearly implicit, local $\delta f$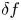 gyrokinetic code is described. Unlike the current approach followed by a number of codes, it treats flow shear continuously in time. In the linear gyrokinetic equation, time-dependences arising from the presence of flow shear are decomposed in such a way that they can be treated explicitly in time with no stringent constraint on the time step. Flow shear related time dependences in the nonlinear term are taken into account exactly, and time dependences in the quasineutrality equation are interpolated. Test cases validating the continuous-in-time implementation in the code GS2 are presented. Lastly, nonlinear gyrokinetic simulations of a JET discharge illustrate the differences observed in turbulent transport compared with the usual, discrete-in-time approach. The continuous-in-time approach is shown, in some cases, to produce fluxes that converge to a different value than with the discrete approach. The new approach can also lead to substantial computational savings by requiring radially narrower boxes. At fixed box size, the continuous implementation is only modestly slower than the previous, discrete approach.
gyrokinetic code is described. Unlike the current approach followed by a number of codes, it treats flow shear continuously in time. In the linear gyrokinetic equation, time-dependences arising from the presence of flow shear are decomposed in such a way that they can be treated explicitly in time with no stringent constraint on the time step. Flow shear related time dependences in the nonlinear term are taken into account exactly, and time dependences in the quasineutrality equation are interpolated. Test cases validating the continuous-in-time implementation in the code GS2 are presented. Lastly, nonlinear gyrokinetic simulations of a JET discharge illustrate the differences observed in turbulent transport compared with the usual, discrete-in-time approach. The continuous-in-time approach is shown, in some cases, to produce fluxes that converge to a different value than with the discrete approach. The new approach can also lead to substantial computational savings by requiring radially narrower boxes. At fixed box size, the continuous implementation is only modestly slower than the previous, discrete approach.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 6
- Cited by



