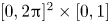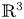1 Introduction
The toroidal geometry, topologically characterised by a single hole and homeomorphic to a continuous surface formed by rotating a circle about an axis external to its plane, is fundamental in plasma physics due to its inherent capacity to provide closed magnetic flux surfaces, essential for confining and stabilising plasmas in magnetic fusion devices. In that context, any study of confinement, coil engineering, stability and transport relies on the description of a magnetic field in a toroidal domain.
Using coordinates may not be the only possible choice to describe magnetic fields in a toroidal geometry. For instance, some codes employ the surface integral method, such as BIEST (O'Neil & Cerfon Reference O'Neil and Cerfon2018; Malhotra et al. Reference Malhotra, Cerfon, Imbert-Gérard and O'Neil2019), which represents the magnetic field using the generalised Debye source formulation. On the other hand, many different kinds of coordinate systems may be used, some of which are not boundary conforming. For example, M3D-C1 (Jardin Reference Jardin2004) exploits an unstructured cylindrical grid because of the advantages of not having a coordinate singularity. Furthermore, cylindrical coordinates $(R, \phi, Z)$![]() are the natural choice for describing a toroidal geometry owing to their close correspondence to a laboratory frame and due to their simplicity in applying boundary conditions. Such constraints can be imposed via boundary-conforming coordinate systems that are designed to align precisely with the boundaries of the domain.
are the natural choice for describing a toroidal geometry owing to their close correspondence to a laboratory frame and due to their simplicity in applying boundary conditions. Such constraints can be imposed via boundary-conforming coordinate systems that are designed to align precisely with the boundaries of the domain.
The construction of a polar-like coordinate grid, or coordinate mapping that is boundary conforming, can be made explicit by the input boundary representing the outermost surface of a set of non-intersecting nested torus-shaped surfaces, such that a monotonically increasing radial coordinate exists with a starting point identifying the coordinates axis. This class of coordinate maps is very common in computations of magnetohydrodynamics (MHD) equilibria.
Given the double periodicity of toroidal boundaries, spectral methods (Matsushima & Marcus Reference Matsushima and Marcus1995) are a popular choice. These methods construct coordinates through a linear combination of global basis functions, expressing cylindrical coordinates $(R, \phi, Z)$![]() in terms of generalised toroidal-like coordinates $(s, \theta, \zeta )$
in terms of generalised toroidal-like coordinates $(s, \theta, \zeta )$![]() via Fourier–polynomial decomposition. Here, $s$
via Fourier–polynomial decomposition. Here, $s$![]() constitutes the monotonically increasing radial coordinate with $\theta$
constitutes the monotonically increasing radial coordinate with $\theta$![]() and $\zeta$
and $\zeta$![]() being some general poloidal and toroidal angles. The main challenge resides in being able to correctly choose the coefficients for the basis functions in such a way that the mapping becomes bijective.
being some general poloidal and toroidal angles. The main challenge resides in being able to correctly choose the coefficients for the basis functions in such a way that the mapping becomes bijective.
The challenges of such task are well depicted by codes routinely used for computing three-dimensional equilibria, in stellarators and tokamaks, such as VMEC (Hirshman & Whitson Reference Hirshman and Whitson1983), GVEC (Hindenlang et al. Reference Hindenlang, Maj, Strumberger, Rampp and Sonnendrücker2019), SPEC (Hudson et al. Reference Hudson, Dewar, Dennis, Hole, McGann, Von Nessi and Lazerson2012; Loizu, Hudson & Nührenberg Reference Loizu, Hudson and Nührenberg2016) or DESC (Dudt & Kolemen Reference Dudt and Kolemen2020; Conlin et al. Reference Conlin, Dudt, Panici and Kolemen2023). These codes solve the inverse problem of finding an equilibrium provided a choice for the flux surfaces.
Extreme three-dimensional (3-D) shaping poses a challenge for the numerical codes. Such boundaries are, for example, obtained from the near-axis expansion method (Jorge, Sengupta & Landreman Reference Jorge, Sengupta and Landreman2020), for which an approximate semi-analytic expression for the equilibrium magnetic field is quickly obtained and the large configuration space of stellarator equilibria can be rapidly explored and optimised (Rodríguez, Sengupta & Bhattacharjee Reference Rodríguez, Sengupta and Bhattacharjee2023). Using the near-axis expansion, very attractive stellarator configurations have been discovered. Examples include quasi-isodynamic configurations with small numbers of field periods (Landreman, Medasani & Zhu Reference Landreman, Medasani and Zhu2021; Jorge et al. Reference Jorge, Plunk, Drevlak, Landreman, Lobsien, Mata and Helander2022; Mata, Plunk & Jorge Reference Mata, Plunk and Jorge2022), or the first reported quasi-helically symmetric configuration to have only 2 field periods (Landreman Reference Landreman2022) (see figures 1 and 2).

Figure 1. A quasi-helically symmetric stellarator surface with magnetic field intensity $|\textbf{B}|$![]() as obtained in Landreman (Reference Landreman2022), seen from above (upper left), left side (bottom left) and from the back (bottom right). Reproduced from Landreman (Reference Landreman2022) with permission.
as obtained in Landreman (Reference Landreman2022), seen from above (upper left), left side (bottom left) and from the back (bottom right). Reproduced from Landreman (Reference Landreman2022) with permission.

Figure 2. Different cross-sections for the same configuration as in figure 1 for different toroidal angles.
These highly optimised configurations are invariably also strongly shaped. They are often characterised by strong poloidal elongations with significant ellipticity and torsion of the magnetic axis. The more exact MHD equilibrium codes are still crucial for globally validating the near-axis results, posing a challenge; indeed, for the case shown in figures 1 and 2, some of the codes have been reported to fail by producing overlapping flux surfaces.
The problem was identified to be associated with how each code initialises the equilibrium calculation by interpolating between the boundary and the axis, leading to overlapping coordinate surfaces. An improved method for choosing the coordinate axis proposed in Qu et al. (Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020) partially prevented coordinate surfaces from intersecting. However, this procedure still fails for arbitrarily strongly shaped boundaries. The perturbation-continuation methods introduced in Conlin et al. (Reference Conlin, Dudt, Panici and Kolemen2023) construct a sequence of equilibria of increasingly complex shaping to arrive at the final highly shaped equilibrium (Nies et al. Reference Nies, Paul, Panici, Hudson and Bhattacharjee2024). In more mathematical terms, we seek the conformal map of a simply connected domain, with a Jordan curve as a boundary, to the unit disc. The mapping is proven to exist (the Osgood–Carathéodory theorem Henrici Reference Henrici1993); however, finding the numerical conformal map is not trivial, as shown in Trefethen (Reference Trefethen2020) and Porter (Reference Porter2005).
In this paper, we propose a new method for constructing polar-like and boundary-conforming coordinates, which enables the computation of grids in smooth and non-intersecting strongly shaped boundaries by exploiting a variational principle. Despite providing a solution to a plasma-physics-driven problem, this construction can be applied to other fields where coordinate mappings in strongly shaped cross-sections are needed, e.g. for blood flow simulation (Zhang et al. Reference Zhang, Bazilevs, Goswami, Bajaj and Hughes2007).
The paper is organised as follows. In § 2, we introduce an action $\mathcal {S}$![]() and we develop the formalism for the mapping given as input the boundary surface, illustrating the main reasons why we expect the extremal points of the functional to be consistent with a mapping for which the coordinate surfaces are non-overlapping. In § 3, looking at the stationary points in $\mathcal {S}$
and we develop the formalism for the mapping given as input the boundary surface, illustrating the main reasons why we expect the extremal points of the functional to be consistent with a mapping for which the coordinate surfaces are non-overlapping. In § 3, looking at the stationary points in $\mathcal {S}$![]() , we derive and comment the Euler–Lagrange (EL) equations. In § 4, representing the mapping in a Fourier–Zernike basis and exploiting the geometrical meaning of the core terms in the Lagrangian, we provide a numerical method for the coordinate construction. In § 5, we illustrate the results obtained by starting from ill-posed coordinate grids both with axisymmetric and non-axisymmetric external boundaries. The application of our coordinate construction to the computation of vacuum 3-D equilibria by GVEC is illustrated in § 6. Finally, a discussion is presented in § 7.
, we derive and comment the Euler–Lagrange (EL) equations. In § 4, representing the mapping in a Fourier–Zernike basis and exploiting the geometrical meaning of the core terms in the Lagrangian, we provide a numerical method for the coordinate construction. In § 5, we illustrate the results obtained by starting from ill-posed coordinate grids both with axisymmetric and non-axisymmetric external boundaries. The application of our coordinate construction to the computation of vacuum 3-D equilibria by GVEC is illustrated in § 6. Finally, a discussion is presented in § 7.
2 Continuous action integral
We will consider general mappings $\boldsymbol {x}(s, \theta, \zeta )$![]() between $(s, \theta, \zeta )$
between $(s, \theta, \zeta )$![]() with $s \in [0, 1]$
with $s \in [0, 1]$![]() , $\theta$
, $\theta$![]() , $\zeta \in [0, 2 {\rm \pi})$
, $\zeta \in [0, 2 {\rm \pi})$![]() and $\mathbb {R}^3$
and $\mathbb {R}^3$![]() , analytic, and double periodic in $\theta$
, analytic, and double periodic in $\theta$![]() , and $\zeta$
, and $\zeta$![]() , $\boldsymbol {x}(s, \theta, \zeta ) = \boldsymbol {x}(s, \theta + 2{\rm \pi}, \zeta ) = \boldsymbol {x}(s, \theta, \zeta + 2 {\rm \pi})$
, $\boldsymbol {x}(s, \theta, \zeta ) = \boldsymbol {x}(s, \theta + 2{\rm \pi}, \zeta ) = \boldsymbol {x}(s, \theta, \zeta + 2 {\rm \pi})$![]() . Boundary conditions are realised by providing a smooth toroidal external boundary $\boldsymbol {x}_b(\theta, \zeta )$
. Boundary conditions are realised by providing a smooth toroidal external boundary $\boldsymbol {x}_b(\theta, \zeta )$![]() and by requiring that $\boldsymbol {x}(1, \theta, \zeta ) = \boldsymbol {x}_b(\theta, \zeta )$
and by requiring that $\boldsymbol {x}(1, \theta, \zeta ) = \boldsymbol {x}_b(\theta, \zeta )$![]() . A coordinate axis is defined as $\boldsymbol {x}_a(\zeta ) = \boldsymbol {x}(0, \theta, \zeta )$
. A coordinate axis is defined as $\boldsymbol {x}_a(\zeta ) = \boldsymbol {x}(0, \theta, \zeta )$![]() , demanding that the mapping continuously changes its topological structure from surfaces with $s \neq 0$
, demanding that the mapping continuously changes its topological structure from surfaces with $s \neq 0$![]() to a curve in space at $s = 0$
to a curve in space at $s = 0$![]() . This condition creates a coordinate singularity at $\boldsymbol {x}_a$
. This condition creates a coordinate singularity at $\boldsymbol {x}_a$![]() , since for fixed $\zeta$
, since for fixed $\zeta$![]() every $\theta$
every $\theta$![]() corresponds to the same point in real space, analogously to the polar coordinates. The objective of this work is to provide a construction of $\boldsymbol {x}$
corresponds to the same point in real space, analogously to the polar coordinates. The objective of this work is to provide a construction of $\boldsymbol {x}$![]() such that it becomes a polar-like coordinate mapping, defined by having a non-vanishing coordinate Jacobian outside of the coordinate axis. Given such mapping $\boldsymbol {x}(s, \theta, \zeta )$
such that it becomes a polar-like coordinate mapping, defined by having a non-vanishing coordinate Jacobian outside of the coordinate axis. Given such mapping $\boldsymbol {x}(s, \theta, \zeta )$![]() , we can compute the covariant basis vectors $\boldsymbol {e}_s = \partial _s \boldsymbol {x}, \boldsymbol {e}_\theta = \partial _\theta \boldsymbol {x}, \boldsymbol {e}_\zeta = \partial _\zeta \boldsymbol {x}$
, we can compute the covariant basis vectors $\boldsymbol {e}_s = \partial _s \boldsymbol {x}, \boldsymbol {e}_\theta = \partial _\theta \boldsymbol {x}, \boldsymbol {e}_\zeta = \partial _\zeta \boldsymbol {x}$![]() , along with the corresponding metric elements $g_{ij} = \boldsymbol {e}_{i}\boldsymbol {\cdot }\boldsymbol {e}_j$
, along with the corresponding metric elements $g_{ij} = \boldsymbol {e}_{i}\boldsymbol {\cdot }\boldsymbol {e}_j$![]() with $i,j = s, \theta, \zeta$
with $i,j = s, \theta, \zeta$![]() . The Jacobian is given by $\sqrt {g} \equiv \boldsymbol {e}_s \boldsymbol {\cdot } (\boldsymbol {e}_\theta \times \boldsymbol {e}_\zeta )$
. The Jacobian is given by $\sqrt {g} \equiv \boldsymbol {e}_s \boldsymbol {\cdot } (\boldsymbol {e}_\theta \times \boldsymbol {e}_\zeta )$![]() . The Jacobian is defined up to a sign depending on whether the basis vectors form a right- or left-handed coordinate system. The contravariant basis vectors are $\boldsymbol {\nabla } s = \boldsymbol {e}_\theta \times \boldsymbol {e}_{\zeta }/\sqrt {g}$
. The Jacobian is defined up to a sign depending on whether the basis vectors form a right- or left-handed coordinate system. The contravariant basis vectors are $\boldsymbol {\nabla } s = \boldsymbol {e}_\theta \times \boldsymbol {e}_{\zeta }/\sqrt {g}$![]() , $\boldsymbol {\nabla } \theta = \boldsymbol {e}_\zeta \times \boldsymbol {e}_{s}/\sqrt {g}$
, $\boldsymbol {\nabla } \theta = \boldsymbol {e}_\zeta \times \boldsymbol {e}_{s}/\sqrt {g}$![]() and $\boldsymbol {\nabla } \zeta = \boldsymbol {e}_s \times \boldsymbol {e}_{\theta }/\sqrt {g}$
and $\boldsymbol {\nabla } \zeta = \boldsymbol {e}_s \times \boldsymbol {e}_{\theta }/\sqrt {g}$![]() . Considering different explicit forms of $\boldsymbol {x}$
. Considering different explicit forms of $\boldsymbol {x}$![]() in the space of mappings conforming to a boundary leads to different forms of the metric elements.
in the space of mappings conforming to a boundary leads to different forms of the metric elements.
We now introduce a geometrical action $\mathcal {S}$![]() for the mapping $\boldsymbol {x}$
for the mapping $\boldsymbol {x}$![]() constrained to the boundary $\boldsymbol {x}_b$
constrained to the boundary $\boldsymbol {x}_b$![]() as
as
Here, $f(\boldsymbol {x}; s, \theta, \zeta )$![]() is a positive function of the mapping and it can explicitly depend on $(s, \theta, \zeta )$
is a positive function of the mapping and it can explicitly depend on $(s, \theta, \zeta )$![]() . As discussed in § 3, $f$
. As discussed in § 3, $f$![]() can be used for fixing the functional form of $\sqrt {g}$
can be used for fixing the functional form of $\sqrt {g}$![]() . A specific form for $f$
. A specific form for $f$![]() given below is chosen to recover the simple case of circular cross-section axisymmetric torus to ensure the polar-like property of $\boldsymbol {x}$
given below is chosen to recover the simple case of circular cross-section axisymmetric torus to ensure the polar-like property of $\boldsymbol {x}$![]() . The parameter $\omega$
. The parameter $\omega$![]() is a constant weighting coefficient. We assert that the minimum of $\mathcal {S}$
is a constant weighting coefficient. We assert that the minimum of $\mathcal {S}$![]() in the space of mappings maximises the set of points in coordinate space where the Jacobian is non-zero.
in the space of mappings maximises the set of points in coordinate space where the Jacobian is non-zero.
The corresponding Lagrangian $\mathcal {L} = \frac {1}{2} f \sqrt {g}^2 + \omega \sqrt {\boldsymbol {e}_s \boldsymbol {\cdot }\boldsymbol {e}_s}$![]() encodes the key geometrical insights that lead to the desired coordinate mapping property. From the analyticity of $\boldsymbol {x}$
encodes the key geometrical insights that lead to the desired coordinate mapping property. From the analyticity of $\boldsymbol {x}$![]() , for having $\sqrt {g} \neq 0$
, for having $\sqrt {g} \neq 0$![]() , it is crucial for the Jacobian to have a uniform sign. Considering that the overall volume $\mathcal {V} = \int {\rm d}\zeta \,{\rm d}\theta \,{\rm d}s \,\sqrt {g}$
, it is crucial for the Jacobian to have a uniform sign. Considering that the overall volume $\mathcal {V} = \int {\rm d}\zeta \,{\rm d}\theta \,{\rm d}s \,\sqrt {g}$![]() is independent of the mapping, if $\sqrt {g}$
is independent of the mapping, if $\sqrt {g}$![]() was decreasing up to becoming negative in a given subset of volume, it must increase somewhere else to counteract the effect, therefore leaving $\mathcal {V}$
was decreasing up to becoming negative in a given subset of volume, it must increase somewhere else to counteract the effect, therefore leaving $\mathcal {V}$![]() constant. Having regions of negative $\sqrt {g}$
constant. Having regions of negative $\sqrt {g}$![]() and positive $\sqrt {g}$
and positive $\sqrt {g}$![]() necessarily leads to larger integrated values of $\sqrt {g}^2$
necessarily leads to larger integrated values of $\sqrt {g}^2$![]() , since there are competing parts of the volume integrand. Moreover, the minimisation of $\sqrt {g}^2$
, since there are competing parts of the volume integrand. Moreover, the minimisation of $\sqrt {g}^2$![]() smooths the regions where $\sqrt {g}$
smooths the regions where $\sqrt {g}$![]() has a peak in its amplitude. Due to volume conservation, the gradients near the regions where the Jacobian is changing sign get weakened up to the point where it reaches homogeneity in sign.
has a peak in its amplitude. Due to volume conservation, the gradients near the regions where the Jacobian is changing sign get weakened up to the point where it reaches homogeneity in sign.
Adding $\omega \sqrt {\boldsymbol {e}_s \boldsymbol {\cdot } \boldsymbol {e}_s}$![]() to the action serves to penalise curvature in the radial coordinate lines, and thus increasing $\omega$
to the action serves to penalise curvature in the radial coordinate lines, and thus increasing $\omega$![]() leads to coordinate mappings with straighter coordinate lines. This contribution to the action was found to be required after an initial numerical exploration suggested that, otherwise, the action functional would be independent of the parametrisation in the poloidal angle coordinate. The proportionality to $\sqrt {g}^2$
leads to coordinate mappings with straighter coordinate lines. This contribution to the action was found to be required after an initial numerical exploration suggested that, otherwise, the action functional would be independent of the parametrisation in the poloidal angle coordinate. The proportionality to $\sqrt {g}^2$![]() , represented by $f$
, represented by $f$![]() , needs to have the same sign of $\omega$
, needs to have the same sign of $\omega$![]() for not introducing any competition between having a constant sign for $\sqrt {g}$
for not introducing any competition between having a constant sign for $\sqrt {g}$![]() and the straightness of coordinate lines. By conventionally choosing to minimise $\mathcal {S}$
and the straightness of coordinate lines. By conventionally choosing to minimise $\mathcal {S}$![]() , we impose $f$
, we impose $f$![]() and $\omega$
and $\omega$![]() to be both positive.
to be both positive.
Note that there are multiple ways to include the boundary constraint $\boldsymbol {x}(1, \theta, \zeta ) = \boldsymbol {x}_{b}(\theta, \zeta )$![]() , e.g. by introducing a Lagrange multiplier $\lambda (\theta, \zeta )$
, e.g. by introducing a Lagrange multiplier $\lambda (\theta, \zeta )$![]() in $\mathcal {S}$
in $\mathcal {S}$![]() via the addition of the term
via the addition of the term
3 Euler–Lagrange equations
In the variational approach, $\boldsymbol {x}$![]() constitutes the dynamic variable independent from $(s, \theta, \zeta )$
constitutes the dynamic variable independent from $(s, \theta, \zeta )$![]() . The relation between $\boldsymbol {x}$
. The relation between $\boldsymbol {x}$![]() and $(s, \theta, \zeta )$
and $(s, \theta, \zeta )$![]() , i.e. the mapping, is recovered by solving the EL equations, analogously to the Lagrangian approach in classical mechanics. We can compute the stationary points in the action $\mathcal {S}$
, i.e. the mapping, is recovered by solving the EL equations, analogously to the Lagrangian approach in classical mechanics. We can compute the stationary points in the action $\mathcal {S}$![]() in (2.1) by considering the variation of the coordinate mapping $\delta \boldsymbol {x} \equiv \boldsymbol {x} - \boldsymbol {x}^{\prime }$
in (2.1) by considering the variation of the coordinate mapping $\delta \boldsymbol {x} \equiv \boldsymbol {x} - \boldsymbol {x}^{\prime }$![]() , where $\boldsymbol {x}$
, where $\boldsymbol {x}$![]() and $\boldsymbol {x}^{\prime }$
and $\boldsymbol {x}^{\prime }$![]() are two independent mappings constrained to $\boldsymbol {x}_b$
are two independent mappings constrained to $\boldsymbol {x}_b$![]() . The boundary conditions fix the possible mapping variations at the external surface, $\delta \boldsymbol {x}(1, \theta, \zeta ) = \delta \boldsymbol {x}_b(\theta, \zeta ) = 0$
. The boundary conditions fix the possible mapping variations at the external surface, $\delta \boldsymbol {x}(1, \theta, \zeta ) = \delta \boldsymbol {x}_b(\theta, \zeta ) = 0$![]() ; and at the coordinate axis, $\delta \boldsymbol {x}(0, \theta, \zeta )$
; and at the coordinate axis, $\delta \boldsymbol {x}(0, \theta, \zeta )$![]() = $\delta \boldsymbol {x}(\zeta )$
= $\delta \boldsymbol {x}(\zeta )$![]() . The variation of the action in (2.1) with respect to the coordinate mapping $\boldsymbol {x}(s, \theta, \zeta )$
. The variation of the action in (2.1) with respect to the coordinate mapping $\boldsymbol {x}(s, \theta, \zeta )$![]() yields the EL equations
yields the EL equations
having defined the curvature vector as $\boldsymbol {\kappa } = \partial _s (\boldsymbol {e}_s / |\boldsymbol {e}_s|)$![]() . It accounts for the variation of the tangential lines along the radial direction, being a measure of the straightness of $\theta,\zeta ={\rm const}$
. It accounts for the variation of the tangential lines along the radial direction, being a measure of the straightness of $\theta,\zeta ={\rm const}$![]() . coordinate lines. The EL equations are a set of nonlinear partial differential equations with boundary conditions. Their derivation is presented in Appendix A. The first term on the left of (3.1) accounts for the volume element compared with a Jacobian that would scale as $1/f$
. coordinate lines. The EL equations are a set of nonlinear partial differential equations with boundary conditions. Their derivation is presented in Appendix A. The first term on the left of (3.1) accounts for the volume element compared with a Jacobian that would scale as $1/f$![]() . The second term is the contribution from the variation of $f$
. The second term is the contribution from the variation of $f$![]() with respect to $\boldsymbol {x}$
with respect to $\boldsymbol {x}$![]() . Lastly, the curvature term represented by $\boldsymbol {\kappa }$
. Lastly, the curvature term represented by $\boldsymbol {\kappa }$![]() and weighted by $\omega$
and weighted by $\omega$![]() , quantifies deviations from straight radial lines.
, quantifies deviations from straight radial lines.
The function $f$![]() can be either externally prescribed or determined by solving (3.1) for a specific choice of $\boldsymbol {x}$
can be either externally prescribed or determined by solving (3.1) for a specific choice of $\boldsymbol {x}$![]() . To fix $f$
. To fix $f$![]() , we impose that the known analytical mapping of a torus with a circular cross-section is recovered exactly by the action minimisation when $\omega$
, we impose that the known analytical mapping of a torus with a circular cross-section is recovered exactly by the action minimisation when $\omega$![]() = 0. The analytical mapping reads as $\boldsymbol {x} = R \, \hat {\boldsymbol {R}} + Z \boldsymbol {e}_z$
= 0. The analytical mapping reads as $\boldsymbol {x} = R \, \hat {\boldsymbol {R}} + Z \boldsymbol {e}_z$![]() , with $\hat {\boldsymbol {R}} = (\cos \phi \boldsymbol {e}_x + \sin \phi \boldsymbol {e}_y)$
, with $\hat {\boldsymbol {R}} = (\cos \phi \boldsymbol {e}_x + \sin \phi \boldsymbol {e}_y)$![]() , $\boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_z$
, $\boldsymbol {e}_x, \boldsymbol {e}_y, \boldsymbol {e}_z$![]() unitary Cartesian vectors, and $R = 1 + s \cos (\theta ),Z=s\sin (\theta )$
unitary Cartesian vectors, and $R = 1 + s \cos (\theta ),Z=s\sin (\theta )$![]() , with $\theta$
, with $\theta$![]() representing the geometrical poloidal angle. For applying the variation approach, we note that, in general, $R$
representing the geometrical poloidal angle. For applying the variation approach, we note that, in general, $R$![]() depends on the coordinate mapping $\boldsymbol {x}$
depends on the coordinate mapping $\boldsymbol {x}$![]() and, implicitly on $s, \theta, \zeta$
and, implicitly on $s, \theta, \zeta$![]() . By choosing
. By choosing
we have $\delta f/ \delta \boldsymbol {x} = - ({2}/{s R^3})\hat {\boldsymbol {R}}$![]() . Substituting this expression into (3.1), the EL equations are trivially satisfied, as intended. Therefore, if $f$
. Substituting this expression into (3.1), the EL equations are trivially satisfied, as intended. Therefore, if $f$![]() is taken as in (3.2) with a circular torus given as a boundary, the minimisation of the action integral will recover the analytic mapping. Given the topological equivalence of toroidal domains with a torus with a circular cross-section, we choose (3.2) to define $f$
is taken as in (3.2) with a circular torus given as a boundary, the minimisation of the action integral will recover the analytic mapping. Given the topological equivalence of toroidal domains with a torus with a circular cross-section, we choose (3.2) to define $f$![]() for the following analysis.
for the following analysis.
4 Numerical implementation
4.1 Zernike–Fourier representation
We consider the local form for the mapping as $\boldsymbol {x} = R(\boldsymbol {x}, s, \theta, \zeta )\,\hat {\boldsymbol {R}} + Z(\boldsymbol {x}, s, \theta, \zeta )\, \boldsymbol {e}_z$![]() . The Jacobian is computed as: $\sqrt {g} = R \sqrt {g}_p = R (\partial _s R \partial _\theta Z - \partial _s Z \partial _\theta R)$
. The Jacobian is computed as: $\sqrt {g} = R \sqrt {g}_p = R (\partial _s R \partial _\theta Z - \partial _s Z \partial _\theta R)$![]() , where $\sqrt {g}_p$
, where $\sqrt {g}_p$![]() is the poloidal part of the Jacobian. The metric elements are $g_{ij} = \partial _i R \partial _j Z + \partial _j R \partial _i Z + \delta _{i\zeta } R^2$
is the poloidal part of the Jacobian. The metric elements are $g_{ij} = \partial _i R \partial _j Z + \partial _j R \partial _i Z + \delta _{i\zeta } R^2$![]() , where $\delta _{i\zeta } = 1$
, where $\delta _{i\zeta } = 1$![]() if $i = \zeta$
if $i = \zeta$![]() and $0$
and $0$![]() otherwise. In addition to considering double-periodic mappings, we impose stellarator symmetry (Lee et al. Reference Lee, Harris, Hirshman and Neilson1988) to simplify the computations. This discrete symmetry is defined as $R(s, -\theta, -\zeta ) = R(s, \theta, \zeta )$
otherwise. In addition to considering double-periodic mappings, we impose stellarator symmetry (Lee et al. Reference Lee, Harris, Hirshman and Neilson1988) to simplify the computations. This discrete symmetry is defined as $R(s, -\theta, -\zeta ) = R(s, \theta, \zeta )$![]() and $Z(s, -\theta, -\zeta ) = -Z(s, \theta, \zeta )$
and $Z(s, -\theta, -\zeta ) = -Z(s, \theta, \zeta )$![]() , which implies a more general symmetry (Dewar & Hudson Reference Dewar and Hudson1998). Stellarators are typically composed of a number of identical sectors $N_{P}$
, which implies a more general symmetry (Dewar & Hudson Reference Dewar and Hudson1998). Stellarators are typically composed of a number of identical sectors $N_{P}$![]() , called field periods. A double-periodic function $h(s, \theta, \zeta )$
, called field periods. A double-periodic function $h(s, \theta, \zeta )$![]() can be expressed in a Fourier–Zernike (McAlinden, McCartney & Moore Reference McAlinden, McCartney and Moore2011) basis as
can be expressed in a Fourier–Zernike (McAlinden, McCartney & Moore Reference McAlinden, McCartney and Moore2011) basis as

where the Zernike polynomials (Niu & Tian Reference Niu and Tian2022) are given as $\mathcal {Z}^{m}_l = \mathcal {R}^m_l \cos (m \theta )$![]() and $\mathcal {Z}^{-m}_l = \mathcal {R}^m_l \sin (m \theta )$
and $\mathcal {Z}^{-m}_l = \mathcal {R}^m_l \sin (m \theta )$![]() , with radial part
, with radial part

for $l\geqslant m$![]() , with $n,l,m \in \mathbb {N}^{+}$
, with $n,l,m \in \mathbb {N}^{+}$![]() . The real coefficients $C_{+, {nlm}}, C_{-,{nlm}}, S_{+, {nlm}}, S_{-, {nlm}}$
. The real coefficients $C_{+, {nlm}}, C_{-,{nlm}}, S_{+, {nlm}}, S_{-, {nlm}}$![]() parametrise the mapping in the Fourier–Zernike space. The Zernike polynomials are orthogonal basis functions on the unit disk, and they can describe the mapping with half of the coefficients used by the parity-restricted Chebyshev polynomials (Mason & Handscomb Reference Mason and Handscomb2002) often used in plasma physics. The normalisation is chosen such that the inner product $\langle A B \rangle = \int _0^1 \int _{0}^{2{\rm \pi} } A(s, \theta ) B(s, \theta ) s \,{\rm d}s\,{\rm d}\theta$
parametrise the mapping in the Fourier–Zernike space. The Zernike polynomials are orthogonal basis functions on the unit disk, and they can describe the mapping with half of the coefficients used by the parity-restricted Chebyshev polynomials (Mason & Handscomb Reference Mason and Handscomb2002) often used in plasma physics. The normalisation is chosen such that the inner product $\langle A B \rangle = \int _0^1 \int _{0}^{2{\rm \pi} } A(s, \theta ) B(s, \theta ) s \,{\rm d}s\,{\rm d}\theta$![]() defined on the space of $\mathcal {L}^2$
defined on the space of $\mathcal {L}^2$![]() functions on the disk gives
functions on the disk gives
Stellarator symmetry imposes $\mathcal {C}_{-, {nlm}} = \mathcal {S}_{+, {nlm}} = 0$![]() for $R$
for $R$![]() and $\mathcal {C}_{+, {nlm}}= \mathcal {S}_{-, {nlm}} = 0$
and $\mathcal {C}_{+, {nlm}}= \mathcal {S}_{-, {nlm}} = 0$![]() for $Z$
for $Z$![]() . Extending the sum to negative values of $n$
. Extending the sum to negative values of $n$![]() , and redefining the set of Fourier–Zernike coefficients in terms of $r_{nlm}, z_{nlm}$
, and redefining the set of Fourier–Zernike coefficients in terms of $r_{nlm}, z_{nlm}$![]() and $n \in \mathbb {Z}$
and $n \in \mathbb {Z}$![]() , the discretised mapping becomes(Qu et al. Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020)
, the discretised mapping becomes(Qu et al. Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020)


where $N$![]() , $M$
, $M$![]() and $L \in \mathbb {N}^{+}$
and $L \in \mathbb {N}^{+}$![]() indicate the resolution imposed in the Fourier–Zernike space. The number of components in $r_{nlm}$
indicate the resolution imposed in the Fourier–Zernike space. The number of components in $r_{nlm}$![]() and $z_{nlm}$
and $z_{nlm}$![]() scales as $2 M^2 N$
scales as $2 M^2 N$![]() . The Fourier–Zernike mapping in the poloidal plane directly satisfies the condition to be analytic (Boyd & Yu Reference Boyd and Yu2011) since the radial part with poloidal mode number $m$
. The Fourier–Zernike mapping in the poloidal plane directly satisfies the condition to be analytic (Boyd & Yu Reference Boyd and Yu2011) since the radial part with poloidal mode number $m$![]() scales as $\mathcal {R}^m_l(s) \sim s^m(\mathcal {R}^{m}_{0} + \mathcal {R}^m_2 s^2 + \mathcal {R}^m_4 s^4 + \dots )$
scales as $\mathcal {R}^m_l(s) \sim s^m(\mathcal {R}^{m}_{0} + \mathcal {R}^m_2 s^2 + \mathcal {R}^m_4 s^4 + \dots )$![]() . Therefore, no special treatment in terms of coordinate regularisation is required for the coordinate axis, where the coordinate mapping will be polar-like at the leading order. The boundary surface $\boldsymbol {x}_b(\theta, \zeta )$
. Therefore, no special treatment in terms of coordinate regularisation is required for the coordinate axis, where the coordinate mapping will be polar-like at the leading order. The boundary surface $\boldsymbol {x}_b(\theta, \zeta )$![]() is given in terms of its Fourier components
is given in terms of its Fourier components


where $N_b, M_b \in \mathbb {N}^{+}$![]() are the prescribed toroidal and poloidal boundary resolutions. In the following, we consider $M= L$
are the prescribed toroidal and poloidal boundary resolutions. In the following, we consider $M= L$![]() . The boundary condition $\boldsymbol {x}(1, \theta, \zeta ) = \boldsymbol {x}_{b}(\theta, \zeta )$
. The boundary condition $\boldsymbol {x}(1, \theta, \zeta ) = \boldsymbol {x}_{b}(\theta, \zeta )$![]() reduces the number of independent components in $r_{nlm}$
reduces the number of independent components in $r_{nlm}$![]() and $z_{nlm}$
and $z_{nlm}$![]() . Using the property for the Zernike radial part of $\mathcal {R}_l^m(1) = 1$
. Using the property for the Zernike radial part of $\mathcal {R}_l^m(1) = 1$![]() for each $m,l$
for each $m,l$![]() , the explicit form for the boundary condition becomes
, the explicit form for the boundary condition becomes

These equations are exploited to fix $(M + 1)(2N + 1)$![]() components of $r_{nlm}$
components of $r_{nlm}$![]() and $z_{nlm}$
and $z_{nlm}$![]() . The coefficients $r_{nmm}$
. The coefficients $r_{nmm}$![]() and $z_{nmm}$
and $z_{nmm}$![]() for each $n$
for each $n$![]() and $m$
and $m$![]() are indeed fixed as $r_{nmm} = R^{b}_{nm} - \sum _{l = m + 1}^{L}r_{nlm}$
are indeed fixed as $r_{nmm} = R^{b}_{nm} - \sum _{l = m + 1}^{L}r_{nlm}$![]() , $z_{nmm} = Z^{b}_{nm} - \sum _{l = m + 1}^{L}z_{nlm}$
, $z_{nmm} = Z^{b}_{nm} - \sum _{l = m + 1}^{L}z_{nlm}$![]() .
.
4.2 Action discretisation
Instead of directly using the Zernike–Fourier representation of the mapping in (2.1), exploiting a coordinate grid highlights the geometrical properties of $\mathcal {S}$![]() in terms of areas and radial lengths. The idea is depicted in the illustration provided in figure 3.
in terms of areas and radial lengths. The idea is depicted in the illustration provided in figure 3.

Figure 3. Schematic illustration of the geometrical elements in the action discretisation.
As drawn under $(a)$![]() , starting with a grid $\{s_i, \theta _j, \zeta _k\}$
, starting with a grid $\{s_i, \theta _j, \zeta _k\}$![]() in coordinate space with $i \in [0, N_s]$
in coordinate space with $i \in [0, N_s]$![]() , $j \in [0, N_\theta ]$
, $j \in [0, N_\theta ]$![]() and $k \in [0, N_{\zeta }]$
and $k \in [0, N_{\zeta }]$![]() , $\boldsymbol {x}$
, $\boldsymbol {x}$![]() maps the corresponding points into a grid of $R_{ijk}$
maps the corresponding points into a grid of $R_{ijk}$![]() and $Z_{ijk}$
and $Z_{ijk}$![]() . Fixing a toroidal angle $\zeta _k$
. Fixing a toroidal angle $\zeta _k$![]() , the grid in the poloidal plane is illustrated in figure 3(b). Connecting the points with straight lines along the coordinate lines we have a set of quadrilaterals and triangles. Each of them has an area $\mathcal {A}_{ijk}$
, the grid in the poloidal plane is illustrated in figure 3(b). Connecting the points with straight lines along the coordinate lines we have a set of quadrilaterals and triangles. Each of them has an area $\mathcal {A}_{ijk}$![]() constituted by the grid points $\boldsymbol {x}_{ijk}$
constituted by the grid points $\boldsymbol {x}_{ijk}$![]() , $\boldsymbol {x}_{i + {1 j k}}$
, $\boldsymbol {x}_{i + {1 j k}}$![]() , $\boldsymbol {x}_{i + 1 j+1 k}$
, $\boldsymbol {x}_{i + 1 j+1 k}$![]() and $\boldsymbol {x}_{i j+1 k}$
and $\boldsymbol {x}_{i j+1 k}$![]() . At the coordinate axis, for which $i = 0$
. At the coordinate axis, for which $i = 0$![]() , we have that $\boldsymbol {x}_{0 j+1 k} = \boldsymbol {x}_{0 j k}$
, we have that $\boldsymbol {x}_{0 j+1 k} = \boldsymbol {x}_{0 j k}$![]() . The expression of $\mathcal {A}_{ijk}$
. The expression of $\mathcal {A}_{ijk}$![]() is explicitly given by the Shoelace formula (Braden Reference Braden1986). Each point $\boldsymbol {x}_{ijk}$
is explicitly given by the Shoelace formula (Braden Reference Braden1986). Each point $\boldsymbol {x}_{ijk}$![]() identifies a radial length $L_{ijk}$
identifies a radial length $L_{ijk}$![]() to $\boldsymbol {x}_{i+1jk}$
to $\boldsymbol {x}_{i+1jk}$![]() via the Euclidean distance of two points. The convention assumed for the identification of each grid point in $\mathcal {A}_{ijk}$
via the Euclidean distance of two points. The convention assumed for the identification of each grid point in $\mathcal {A}_{ijk}$![]() and in $L_{ijk}$
and in $L_{ijk}$![]() is shown in figure 3. Given a point $\boldsymbol {x}_{ijk}$
is shown in figure 3. Given a point $\boldsymbol {x}_{ijk}$![]() the points at $i + 1$
the points at $i + 1$![]() and $j + 1$
and $j + 1$![]() correspond to the incremental radial and poloidal coordinates, respectively. For this reason, $\mathcal {A}_{ijk}$
correspond to the incremental radial and poloidal coordinates, respectively. For this reason, $\mathcal {A}_{ijk}$![]() and $L_{ijk}$
and $L_{ijk}$![]() are not defined at the boundary.
are not defined at the boundary.
By choosing $f$![]() following (3.2), the Jacobian reduces to a poloidal Jacobian, such that $f \sqrt {g}^2 = \sqrt {g}_p^2/s$
following (3.2), the Jacobian reduces to a poloidal Jacobian, such that $f \sqrt {g}^2 = \sqrt {g}_p^2/s$![]() . Thus, the discrete action integral can be computed as
. Thus, the discrete action integral can be computed as

where we approximated the poloidal Jacobian with the area element, considered an equispaced grid, and neglected common multiplicative factors. Here, $\mathcal {S}[\boldsymbol {x}_{ijk}]$![]() is an explicit function in terms of the free variables $\{r_{nlm}, z_{nlm}\}$
is an explicit function in terms of the free variables $\{r_{nlm}, z_{nlm}\}$![]() . Minimising $\mathcal {S}$
. Minimising $\mathcal {S}$![]() is an unconstrained nonlinear optimisation problem that we solve using the Broyden–Fletcher–Goldfarb–Shanno algorithm (Dai Reference Dai2002), a descent-gradient iterative method with an explicit computation of the gradient in the space of free parameters as illustrated in Appendix F.
is an unconstrained nonlinear optimisation problem that we solve using the Broyden–Fletcher–Goldfarb–Shanno algorithm (Dai Reference Dai2002), a descent-gradient iterative method with an explicit computation of the gradient in the space of free parameters as illustrated in Appendix F.
5 Results
5.1 Axisymmetry
To validate the action-based approach, we first consider the coordinate construction for axisymmetric boundary surfaces both analytically and numerically. Exploiting the inherent symmetry along the toroidal angle, we transform the problem into one that is focused on optimising the Jacobian within a single poloidal plane. The toroidal index is left out for simplicity.
We consider the family of boundaries, proposed in Qu et al. (Reference Qu, Pfefferlé, Hudson, Baillod, Kumar, Dewar and Hole2020), parameterised as $R^b(\theta ) = R_0^b + R_1^b \cos \theta + R_2^b \cos 2\theta$![]() and $Z^b(\theta ) = Z_0^b + Z_1^b \sin \theta + Z_2^b \sin 2\theta$
and $Z^b(\theta ) = Z_0^b + Z_1^b \sin \theta + Z_2^b \sin 2\theta$![]() . We consider a poloidal mapping $\boldsymbol {x}(s, \theta )$
. We consider a poloidal mapping $\boldsymbol {x}(s, \theta )$![]() with a Zernike polynomial of order $L = 2$
with a Zernike polynomial of order $L = 2$![]() . Combining with boundary conditions, we get: $R(s, \theta ) = R_0^b + 2 r_{20}(s^2 - 1) + R_1^b s \cos \theta + R_2^b s^2 \cos 2 \theta$
. Combining with boundary conditions, we get: $R(s, \theta ) = R_0^b + 2 r_{20}(s^2 - 1) + R_1^b s \cos \theta + R_2^b s^2 \cos 2 \theta$![]() , $Z(s, \theta ) = Z_0^b + Z_1^b s \sin \theta + Z_2^b s^2 \sin 2 \theta$
, $Z(s, \theta ) = Z_0^b + Z_1^b s \sin \theta + Z_2^b s^2 \sin 2 \theta$![]() . The only degree of freedom is $r_{20}$
. The only degree of freedom is $r_{20}$![]() . The action $\mathcal {S}[r_{20}]$
. The action $\mathcal {S}[r_{20}]$![]() is a second-order polynomial in $r_{20}$
is a second-order polynomial in $r_{20}$![]() plus a contribution from the integrated radial length proportional to $\omega$
plus a contribution from the integrated radial length proportional to $\omega$![]() . In the numerical implementation we set $M = L = 2$
. In the numerical implementation we set $M = L = 2$![]() , $N_{s} \times N_\theta = 1000 \times 1000$
, $N_{s} \times N_\theta = 1000 \times 1000$![]() .
.
Firstly, as a sanity check for the numerical implementation, we take $\boldsymbol {x}_b$![]() as a torus with circular cross-section, $R_0^b = 2$
as a torus with circular cross-section, $R_0^b = 2$![]() , $R_1^b = Z_1^b = 1$
, $R_1^b = Z_1^b = 1$![]() and $R_2^b = Z_2^b = 0$
and $R_2^b = Z_2^b = 0$![]() . The action becomes $\mathcal {S}[r_{20}] = {\rm \pi}( 1 + 4 r_{20}^2) + \omega \int _{0}^{2{\rm \pi} }{\rm d}\theta \,\int _0^{1} {\rm d}s\,\sqrt {16 r_{20}^2 s^2 + 8 s r_{20} \cos \theta + 1}$
. The action becomes $\mathcal {S}[r_{20}] = {\rm \pi}( 1 + 4 r_{20}^2) + \omega \int _{0}^{2{\rm \pi} }{\rm d}\theta \,\int _0^{1} {\rm d}s\,\sqrt {16 r_{20}^2 s^2 + 8 s r_{20} \cos \theta + 1}$![]() . The analytical study of $\mathcal {S}$
. The analytical study of $\mathcal {S}$![]() shows a global minimum corresponding to optimal $r_{20}$
shows a global minimum corresponding to optimal $r_{20}$![]() values between $0$
values between $0$![]() and $10^{-10}$
and $10^{-10}$![]() . Figure 4 shows the starting and optimised grids obtained from the numerical optimisation, with a normalised Jacobian $\sqrt {g}_N/s=\sqrt {g}/(\max (\sqrt {g})s)$
. Figure 4 shows the starting and optimised grids obtained from the numerical optimisation, with a normalised Jacobian $\sqrt {g}_N/s=\sqrt {g}/(\max (\sqrt {g})s)$![]() , being unitary for the circular polar grid. The starting grid on the left has been chosen with an initial coordinate axis outside the external boundary, creating a region with ill-posed coordinates, as $\sqrt {g}_N$
, being unitary for the circular polar grid. The starting grid on the left has been chosen with an initial coordinate axis outside the external boundary, creating a region with ill-posed coordinates, as $\sqrt {g}_N$![]() becomes negative with overlapping coordinate lines. As shown in figure 4, the algorithm finds the polar coordinate in the poloidal plane as expected, with $\sqrt {g}_N/s$
becomes negative with overlapping coordinate lines. As shown in figure 4, the algorithm finds the polar coordinate in the poloidal plane as expected, with $\sqrt {g}_N/s$![]() being unitary in all the domain. The parameter $\boldsymbol {x}(s, \theta, \zeta )$
being unitary in all the domain. The parameter $\boldsymbol {x}(s, \theta, \zeta )$![]() retrieves the toroidal coordinate with Jacobian $s (R_2^b + s \cos \theta )$
retrieves the toroidal coordinate with Jacobian $s (R_2^b + s \cos \theta )$![]() as in figure 4 on the right. The plotted results are for $\omega = 10^{-1}$
as in figure 4 on the right. The plotted results are for $\omega = 10^{-1}$![]() , and its variation does not affect the final result significantly as the analytical discussion anticipated.
, and its variation does not affect the final result significantly as the analytical discussion anticipated.

Figure 4. Normalised Jacobian $\sqrt {g}_N/s$![]() (in colour) and constant coordinate lines (in grey) for a circular torus and the external boundary (in red). The coordinate axis is dotted in blue. The initial grid on the left with initial action value $\mathcal {S}_i$
(in colour) and constant coordinate lines (in grey) for a circular torus and the external boundary (in red). The coordinate axis is dotted in blue. The initial grid on the left with initial action value $\mathcal {S}_i$![]() is compared with the optimisation outcome with $\mathcal {S}_f$
is compared with the optimisation outcome with $\mathcal {S}_f$![]() . In the right plot, the 3-D Jacobian is shown (including the R factor as explained in the text above) with $\mathcal {S}_T$
. In the right plot, the 3-D Jacobian is shown (including the R factor as explained in the text above) with $\mathcal {S}_T$![]() being the final value of optimisation.
being the final value of optimisation.
Next, a strongly shaped boundary is considered, in particular a bean-shaped contour described by $R_0^b = 1$![]() $Z_0^b = 0$
$Z_0^b = 0$![]() , $R_1^b = 0.6$
, $R_1^b = 0.6$![]() , $Z_1^b = 0.8$
, $Z_1^b = 0.8$![]() , $R_2^b = 0.8$
, $R_2^b = 0.8$![]() and $Z_2^b = 0.1$
and $Z_2^b = 0.1$![]() . Considering $\omega = 0$
. Considering $\omega = 0$![]() , the minimum of the poloidal action is found analytically at $r_{20} = -0.42$
, the minimum of the poloidal action is found analytically at $r_{20} = -0.42$![]() . Initiated with $r_{20} = 0.2$
. Initiated with $r_{20} = 0.2$![]() , the coordinate lines in the initial grid, shown in figure 5, exhibit significant overlap, resulting in a negative Jacobian. The minimisation algorithm yields a valid mapping aligned with the analytical prediction, as in the centre and right plots in figure 5 illustrate. Subsequent increments in the $(s, \theta )$
, the coordinate lines in the initial grid, shown in figure 5, exhibit significant overlap, resulting in a negative Jacobian. The minimisation algorithm yields a valid mapping aligned with the analytical prediction, as in the centre and right plots in figure 5 illustrate. Subsequent increments in the $(s, \theta )$![]() grid resolution leads to the minimisation of the action $\mathcal {S}_{f}$
grid resolution leads to the minimisation of the action $\mathcal {S}_{f}$![]() asymptotically reaching the analytical value $\mathcal {S}_A = 0.298$
asymptotically reaching the analytical value $\mathcal {S}_A = 0.298$![]() . Low values for the radial weight $\omega$
. Low values for the radial weight $\omega$![]() allow for more curved coordinate lines, as figure 6 shows, whereas increasing $\omega$
allow for more curved coordinate lines, as figure 6 shows, whereas increasing $\omega$![]() straightens radial coordinate lines and shifts the coordinate axis to the left. In the limit of large $\omega$
straightens radial coordinate lines and shifts the coordinate axis to the left. In the limit of large $\omega$![]() , the optimal mapping is mostly influenced by the straightness of the coordinate lines, leading to possibly ill-posed results (data not shown). The maximum value of $\omega$
, the optimal mapping is mostly influenced by the straightness of the coordinate lines, leading to possibly ill-posed results (data not shown). The maximum value of $\omega$![]() is, in general, problem-dependent, being influenced by the boundary shape and by the area of the cross-section.
is, in general, problem-dependent, being influenced by the boundary shape and by the area of the cross-section.

Figure 5. Normalised Jacobian $\sqrt {g}_N/s$![]() (in colour) and constant coordinate lines (in grey) for the bean-shaped external boundary (in red). The coordinate axis is dotted in blue. The initial grid on the left with initial action value $\mathcal {S}_i$
(in colour) and constant coordinate lines (in grey) for the bean-shaped external boundary (in red). The coordinate axis is dotted in blue. The initial grid on the left with initial action value $\mathcal {S}_i$![]() is compared with the outcome of the optimisation with $\mathcal {S}_f$
is compared with the outcome of the optimisation with $\mathcal {S}_f$![]() and the analytical result $\mathcal {S}_A$
and the analytical result $\mathcal {S}_A$![]() .
.

Figure 6. Comparison of optimised configurations for increasing values of $\omega$![]() . Plotted are the normalised Jacobian $\sqrt {g}_N/s$
. Plotted are the normalised Jacobian $\sqrt {g}_N/s$![]() (in colour) and constant coordinate lines (in grey) for the bean-shaped external boundary (in red). The coordinate axis is dotted in blue.
(in colour) and constant coordinate lines (in grey) for the bean-shaped external boundary (in red). The coordinate axis is dotted in blue.
5.2 Non-axisymmetry
The strongly shaped boundary in figure 1 provides a non-axisymmetric test where the conventional coordinate construction using a polynomial interpolation from the boundary fails. The optimisation here is performed with $M = N = L = 5$![]() and $N_{s} \times N_\theta \times N_\zeta = 80 \times 50 \times 80$
and $N_{s} \times N_\theta \times N_\zeta = 80 \times 50 \times 80$![]() with $\omega = 10^{-2}$
with $\omega = 10^{-2}$![]() . The initial grid is computed by setting all the degrees of freedom to zero. Figure 7 shows that coordinate singularities in the initial grids (top panel with starting action value $\mathcal {S}_i = 1$
. The initial grid is computed by setting all the degrees of freedom to zero. Figure 7 shows that coordinate singularities in the initial grids (top panel with starting action value $\mathcal {S}_i = 1$![]() ) are avoided by the optimisation algorithm (bottom panel with final action value $\mathcal {S}_f = 0.752$
) are avoided by the optimisation algorithm (bottom panel with final action value $\mathcal {S}_f = 0.752$![]() ). We would like to remark that, given a value of $\omega$
). We would like to remark that, given a value of $\omega$![]() and a grid resolution, the algorithm finds this same optimal mapping no matter how bad the initial guess is (data not shown). The same happens in the axisymmetric case, showing the algorithm's robustness.
and a grid resolution, the algorithm finds this same optimal mapping no matter how bad the initial guess is (data not shown). The same happens in the axisymmetric case, showing the algorithm's robustness.

Figure 7. Comparison between the starting (a–c) and optimised (d–f) configurations at different toroidal planes. Plotted are the normalised Jacobian $\sqrt {g}_N/s$![]() (in colour) and constant coordinate lines (in grey) for a strongly shaped boundary (in red). The coordinate axis is dotted in blue. The different figures use different axis scaling, which distorts the real-space appearance.
(in colour) and constant coordinate lines (in grey) for a strongly shaped boundary (in red). The coordinate axis is dotted in blue. The different figures use different axis scaling, which distorts the real-space appearance.
5.3 Numerical verification of the EL equations
Given a mapping $\boldsymbol {x}$![]() we can provide a measure of its distance from the theoretical extremal point of $\mathcal {S}$
we can provide a measure of its distance from the theoretical extremal point of $\mathcal {S}$![]() via the EL equations (3.1). Defining the operator $\boldsymbol {\mathcal {L}}(\boldsymbol {x})$
via the EL equations (3.1). Defining the operator $\boldsymbol {\mathcal {L}}(\boldsymbol {x})$![]() as the left side of (3.1), we consider the volume average
as the left side of (3.1), we consider the volume average
where $V$![]() is the volume which depends solely on the boundary. Here, $\langle s^4 \boldsymbol {\mathcal {L}}^2 \rangle$
is the volume which depends solely on the boundary. Here, $\langle s^4 \boldsymbol {\mathcal {L}}^2 \rangle$![]() globally quantifies the deviation of the mapping from the extremal solution. Introducing the $s^2$
globally quantifies the deviation of the mapping from the extremal solution. Introducing the $s^2$![]() factor ensures numerical stability near the axis, as ${\rm d}f/{\rm d}s \sim 1/s^2$
factor ensures numerical stability near the axis, as ${\rm d}f/{\rm d}s \sim 1/s^2$![]() .
.
In figure 8, we observe that increasing the Zernike–Fourier discretisation, equivalent to having a higher number of free parameters $N_{dof}$![]() in the optimisation, results in a better approximation of the mapping solution, both in axisymmetric and non-axisymmetric cases for strongly shaped boundaries. Both cases show an exponential convergence, resulting from the spectral representation of $\boldsymbol {x}$
in the optimisation, results in a better approximation of the mapping solution, both in axisymmetric and non-axisymmetric cases for strongly shaped boundaries. Both cases show an exponential convergence, resulting from the spectral representation of $\boldsymbol {x}$![]() , with the axisymmetric geometry being faster owing to simpler geometry. Notably, $\mathcal {L}^2$
, with the axisymmetric geometry being faster owing to simpler geometry. Notably, $\mathcal {L}^2$![]() deviates from zero primarily near the boundary and where the coordinate lines exhibit rapid variation compared with inner regions (figure 9). This error near the edge is related to the Zernike polynomial's known rapid fluctuations near $s = 1$
deviates from zero primarily near the boundary and where the coordinate lines exhibit rapid variation compared with inner regions (figure 9). This error near the edge is related to the Zernike polynomial's known rapid fluctuations near $s = 1$![]() with increasing radial mode number. The boundary coefficients used for the numerical convergence study in figure 8 can be found in Appendix E.
with increasing radial mode number. The boundary coefficients used for the numerical convergence study in figure 8 can be found in Appendix E.

Figure 8. Convergence of the solution from the discretisation of the numerical action with the increase in the free parameters to the EL stationary point for an axisymmetric case and a non-axisymmetric one.

Figure 9. The value of $\mathcal {L}^2$![]() is analysed locally for $N_{dof} = 3$
is analysed locally for $N_{dof} = 3$![]() (red circle of figure 8). The coloured regions show $\mathcal {L}^2$
(red circle of figure 8). The coloured regions show $\mathcal {L}^2$![]() normalised to its maximum value.
normalised to its maximum value.
6 GVEC application
The approach of minimising the action functional (A5) is successfully tested in GVEC (Hindenlang et al. Reference Hindenlang, Maj, Strumberger, Rampp and Sonnendrücker2019), a 3-D MHD equilibrium solver assuming closed nested flux surfaces. In GVEC, the flux surface coordinate mapping $R(s,\theta,\zeta ), Z(s,\theta,\zeta )$![]() is discretised by a tensor product of B-splines in $s$
is discretised by a tensor product of B-splines in $s$![]() and Fourier modes in angular directions. Using a $1$
and Fourier modes in angular directions. Using a $1$![]() element B-spline of degree equal to the maximum poloidal mode number, and smoothness constraints at the axis, the Zernike–Fourier representation is exactly recovered. As a 3-D test case, a W7-X-like boundary with an initial circular magnetic axis was taken, where the usual initialisation of GVEC produces an initial state with regions having $\sqrt {g} < 0$
element B-spline of degree equal to the maximum poloidal mode number, and smoothness constraints at the axis, the Zernike–Fourier representation is exactly recovered. As a 3-D test case, a W7-X-like boundary with an initial circular magnetic axis was taken, where the usual initialisation of GVEC produces an initial state with regions having $\sqrt {g} < 0$![]() , as shown in figure 10(a). The maximum Jacobian used for the normalisation is always positive.
, as shown in figure 10(a). The maximum Jacobian used for the normalisation is always positive.

Figure 10. GVEC results for the minimisation of the action functional (A5) using a 3-D W7-X-like boundary and a circular axis for initialisation. The normalised scaled Jacobian is shown in colour, along with the $(s,\theta )$![]() grid for 4 poloidal cross-sections. The mapping is discretised with a Zernike–Fourier representation, using $1$
grid for 4 poloidal cross-sections. The mapping is discretised with a Zernike–Fourier representation, using $1$![]() B-spline element in the radial direction and $(m,n)_\textrm {max}=7$
B-spline element in the radial direction and $(m,n)_\textrm {max}=7$![]() . (a) Initial state with $\sqrt {g}<0$
. (a) Initial state with $\sqrt {g}<0$![]() . (b–d) Valid optimised grids for increasing weighting factor $\omega$
. (b–d) Valid optimised grids for increasing weighting factor $\omega$![]() . Note that $\max (\sqrt {g})$
. Note that $\max (\sqrt {g})$![]() is always positive.
is always positive.
The minimisation of $\mathcal {S}$![]() with a gradient descent successfully produced $\sqrt {g}>0$
with a gradient descent successfully produced $\sqrt {g}>0$![]() . This is shown in figures 10(b), 10(c) and 10(d), where the initial invalid $(s,\theta )$
. This is shown in figures 10(b), 10(c) and 10(d), where the initial invalid $(s,\theta )$![]() grid and final valid grids for different weighting factors $\omega$
grid and final valid grids for different weighting factors $\omega$![]() are shown, as well as the normalised scaled Jacobian.
are shown, as well as the normalised scaled Jacobian.
The free parameter $\omega >0$![]() acts as a penalty term in the minimisation, increasing the straightness of $\theta$
acts as a penalty term in the minimisation, increasing the straightness of $\theta$![]() contours, but its maximum value is not known a priori. The strength of $\omega$
contours, but its maximum value is not known a priori. The strength of $\omega$![]() is a trade-off between the straightness of the $\theta$
is a trade-off between the straightness of the $\theta$![]() -contours, the axis position and consequently also the minimal scaled Jacobian. As seen in figures 10(b)–10(d), for increasing $\omega$
-contours, the axis position and consequently also the minimal scaled Jacobian. As seen in figures 10(b)–10(d), for increasing $\omega$![]() , the $\theta$
, the $\theta$![]() -contours are straightened, at the cost of a smaller minimal Jacobian, being close to zero for $\omega =0.8$
-contours are straightened, at the cost of a smaller minimal Jacobian, being close to zero for $\omega =0.8$![]() . In $(b)$
. In $(b)$![]() , $\omega =0.01$
, $\omega =0.01$![]() leads to a slightly oscillating behaviour of the $\theta$
leads to a slightly oscillating behaviour of the $\theta$![]() -contours. Using these solutions as initialisation for the MHD energy minimisation, it was found that GVEC had no difficulties converging to an equilibrium for moderate $\omega \leqslant 0.2$
-contours. Using these solutions as initialisation for the MHD energy minimisation, it was found that GVEC had no difficulties converging to an equilibrium for moderate $\omega \leqslant 0.2$![]() .
.
7 Discussion
This paper introduces a method for constructing polar-like and boundary-conforming coordinates within arbitrarily shaped toroidal domains based on identifying a mapping that extremises an action formulated from geometric principles. Preserving bijectivity follows from minimising the squared Jacobian (scaled by a positive factor $f$![]() ) and the radial curvature of the mapping. The first variation of $\mathcal {S}$
) and the radial curvature of the mapping. The first variation of $\mathcal {S}$![]() yields a set of nonlinear partial differential equations, balancing a gradient comparing the relative scaling of $f$
yields a set of nonlinear partial differential equations, balancing a gradient comparing the relative scaling of $f$![]() and $\sqrt {g}$
and $\sqrt {g}$![]() , a radial curvature term and the variation of $f$
, a radial curvature term and the variation of $f$![]() with respect to the mapping. The value of $f$
with respect to the mapping. The value of $f$![]() is determined using a topological argument with a torus with a circular cross-section in cylindrical coordinates as a reference.
is determined using a topological argument with a torus with a circular cross-section in cylindrical coordinates as a reference.
Both axisymmetric and non-axisymmetric tests, conducted through analytical and numerical means, demonstrate the effectiveness of minimising $\mathcal {S}$![]() in constructing coordinates for domains with complex shapes. As the poloidal and toroidal discretisation increases, the volume average $\langle s^4 \boldsymbol {\mathcal {L}}^2 \rangle$
in constructing coordinates for domains with complex shapes. As the poloidal and toroidal discretisation increases, the volume average $\langle s^4 \boldsymbol {\mathcal {L}}^2 \rangle$![]() indicates convergence of the optimised mapping towards the EL zero, with notable discrepancies observed, primarily in regions near the boundary where significant variations occur and high resolution is essential. The robustness of the action formalism is further validated by its application in computing 3-D MHD equilibria within the GVEC framework (Hindenlang et al. Reference Hindenlang, Maj, Strumberger, Rampp and Sonnendrücker2019), emphasising its efficacy where alternative coordinate choices need a careful a priori choice of the initial axis position, without the guarantee of yielding a valid mapping.
indicates convergence of the optimised mapping towards the EL zero, with notable discrepancies observed, primarily in regions near the boundary where significant variations occur and high resolution is essential. The robustness of the action formalism is further validated by its application in computing 3-D MHD equilibria within the GVEC framework (Hindenlang et al. Reference Hindenlang, Maj, Strumberger, Rampp and Sonnendrücker2019), emphasising its efficacy where alternative coordinate choices need a careful a priori choice of the initial axis position, without the guarantee of yielding a valid mapping.
A thorough study of the existence of global minima for the action in (2.1), along with an exploration of solutions to the EL equations (3.1), could significantly expedite the computation of the optimal coordinate mapping. Ongoing analysis is directed towards studying the action formalism in the formalism of harmonics maps (Eells & Sampson Reference Eells and Sampson1964; Hamilton Reference Hamilton1975) with their close relation to conformal mappings. Analysing the influence of parameters $f$![]() and $\omega$
and $\omega$![]() on these solutions can provide insights for enhancing the Jacobian in specific regions of a given boundary. While directly solving the EL equations (3.1) instead of employing a global approach based on minimising an action integral may offer faster convergence, the inherent challenge persists due to the nonlinear nature of the problem and the prescribed strongly shaped boundary conditions.
on these solutions can provide insights for enhancing the Jacobian in specific regions of a given boundary. While directly solving the EL equations (3.1) instead of employing a global approach based on minimising an action integral may offer faster convergence, the inherent challenge persists due to the nonlinear nature of the problem and the prescribed strongly shaped boundary conditions.
The findings presented in this paper hold potential value for 3-D MHD equilibrium codes and other codes utilising a global set of toroidal flux coordinates. This method can facilitate the exploration of complex, strongly shaped configurations that were previously challenging to address or enhance the convergence and precision of existing geometries across various applications.
Funding
This work has been carried out within the framework of the EUROfusion Consortium, via the Euratom Research and Training Programme (Grant Agreement No. 101052200 – EUROfusion) and funded by the Swiss State Secretariat for Education, Research and Innovation (SERI). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union, the European Commission, or SERI. Neither the European Union nor the European Commission nor SERI can be held responsible for them. This research was also supported by a grant from the Simons Foundation (1013657, JL). R.K. is supported by the Helmholtz Association under the joint research school ‘Munich School for Data Science’ – MUDS.
The authors thank M. Landreman for providing the strongly shaped boundary in figure 1 that started this work.
Editor Per Helander thanks the referees for their advice in evaluating this article.
Data availability statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Derivation of EL equations
First, we take the variation of the term proportional to the Jacobian squared, leading to


Here, $\delta f / \delta \boldsymbol {x}$![]() is the variation of $f$
is the variation of $f$![]() with respect to the mapping $\boldsymbol {x}$
with respect to the mapping $\boldsymbol {x}$![]() . From the first to the second line, we used the definition of $\sqrt {g}$
. From the first to the second line, we used the definition of $\sqrt {g}$![]() and integrated by parts. In Appendix B, the explicit application of the boundary conditions in the integration by parts is presented. The parameter $\boldsymbol {x}$
and integrated by parts. In Appendix B, the explicit application of the boundary conditions in the integration by parts is presented. The parameter $\boldsymbol {x}$![]() being analytical and $s f$
being analytical and $s f$![]() being finite in the limit of approaching the coordinate axis are sufficient conditions for the vanishing of the local boundary terms. As shown in Appendix C, the last term in (A2) is zero using the Christoffel symbols (Wald Reference Wald2010).
being finite in the limit of approaching the coordinate axis are sufficient conditions for the vanishing of the local boundary terms. As shown in Appendix C, the last term in (A2) is zero using the Christoffel symbols (Wald Reference Wald2010).
Regarding the variation in the radial length

with $\boldsymbol {\kappa } = \partial _s (\boldsymbol {e}_s / |\boldsymbol {e}_s|)$![]() . As illustrated in Appendix D, from analyticity at the coordinate axis the boundary terms from integration by parts vanish. The variation of the action in (2.1) with respect to the coordinate mapping yields
. As illustrated in Appendix D, from analyticity at the coordinate axis the boundary terms from integration by parts vanish. The variation of the action in (2.1) with respect to the coordinate mapping yields
The stationary points of $\mathcal {S}$![]() are obtained when $\delta \mathcal {S}=0$
are obtained when $\delta \mathcal {S}=0$![]() for arbitrary $\delta \boldsymbol {x}$
for arbitrary $\delta \boldsymbol {x}$![]() . Since (A5) holds for arbitrary $\delta \boldsymbol {x}$
. Since (A5) holds for arbitrary $\delta \boldsymbol {x}$![]() satisfying the boundary conditions, implying the vanishing of the expression inside the square brackets for a stationary point, the EL equations for the coordinate mapping $\boldsymbol {x}(s,\theta, \zeta )$
satisfying the boundary conditions, implying the vanishing of the expression inside the square brackets for a stationary point, the EL equations for the coordinate mapping $\boldsymbol {x}(s,\theta, \zeta )$![]() are derived.
are derived.
Appendix B. Boundary terms in the EL equations
We expand the first term on the right side of (A2). Using the definition for $\sqrt {g}$![]()
The integration by parts in $s$![]() leads to
leads to

The local term evaluated at the boundary is zero, since at $s = 1$![]() $\delta \boldsymbol {x}$
$\delta \boldsymbol {x}$![]() vanishes. The term at the axis gives a local contribution that needs to be evaluated in the limit where $s$
vanishes. The term at the axis gives a local contribution that needs to be evaluated in the limit where $s$![]() is zero
is zero
We prove the integrated part in (B3) is zero for each $\delta \boldsymbol {x}$![]() . Since the mapping is analytical near the axis, we have that $\boldsymbol {e}_\theta = 0$
. Since the mapping is analytical near the axis, we have that $\boldsymbol {e}_\theta = 0$![]() and $\boldsymbol {e}_\zeta$
and $\boldsymbol {e}_\zeta$![]() , $\boldsymbol {e}_s$
, $\boldsymbol {e}_s$![]() are finite. We are left to prove that $f \sqrt {g}$
are finite. We are left to prove that $f \sqrt {g}$![]() is finite in the limit of $s$
is finite in the limit of $s$![]() vanishing. This is equivalent to checking that $f \boldsymbol {e}_\theta$
vanishing. This is equivalent to checking that $f \boldsymbol {e}_\theta$![]() is a finite quantity. Using the condition of analyticity at the coordinate axis
is a finite quantity. Using the condition of analyticity at the coordinate axis

where $\partial _s \boldsymbol {x}_a = 0$![]() and with $\partial _{s}^n \boldsymbol {x}$
and with $\partial _{s}^n \boldsymbol {x}$![]() and its derivatives to $\theta$
and its derivatives to $\theta$![]() are well defined. Equation (B4) states that for $f\boldsymbol {e}_\theta$
are well defined. Equation (B4) states that for $f\boldsymbol {e}_\theta$![]() to be defined for $s$
to be defined for $s$![]() going to zero, we need $f s$
going to zero, we need $f s$![]() to either be fixed or go to zero simultaneously. We have that the term in (B3) is zero in these conditions for every $\delta \boldsymbol {x}$
to either be fixed or go to zero simultaneously. We have that the term in (B3) is zero in these conditions for every $\delta \boldsymbol {x}$![]() .
.
Going back to (B1), integrating by parts along the poloidal angle $\partial _\theta \delta \boldsymbol {x} \boldsymbol {\cdot } (\boldsymbol {e}_\theta \times \boldsymbol {e}_\zeta )$![]()

Due to periodicity, the local term is zero. The same steps are applied for the integration over $\zeta$![]() .
.
Appendix C. Useful identities for EL derivation
We now prove that the third term on the right side of (A2) vanishes. To light up the notation and be clearer in the computations, we introduce $\xi ^i$![]() , with $i = 1, 2, 3$
, with $i = 1, 2, 3$![]() as $(s, \theta, \zeta )$
as $(s, \theta, \zeta )$![]() , and $x_i$
, and $x_i$![]() are the Cartesian coordinates for the mapping. We use Einstein's notations, where the sum over repeated indices is omitted
are the Cartesian coordinates for the mapping. We use Einstein's notations, where the sum over repeated indices is omitted
Considering the second term on the right side
Using the identity (Wald Reference Wald2010)
From the Christoffel identity $\varGamma ^i_{ik} = \partial \log \sqrt {g} / \partial x_m$![]() , then
, then
Substituting (C5) into (C4), we obtain that
Giving
Appendix D. Local curvature term
The local term in $s$![]() obtained by integrating by parts the right side of (A4) is
obtained by integrating by parts the right side of (A4) is
Writing it explicitly in the limit of vanishing $s$![]()

and using Ptolemy's identities, the integral in (D2) can be rearranged into

Since $a, b, c, d$![]() are functions only of $\zeta$
are functions only of $\zeta$![]() , we integrate first along $\theta$
, we integrate first along $\theta$![]() treating them as constants. For each term, the integral can be split from $0$
treating them as constants. For each term, the integral can be split from $0$![]() to ${\rm \pi}$
to ${\rm \pi}$![]() and from ${\rm \pi}$
and from ${\rm \pi}$![]() to $2{\rm \pi}$
to $2{\rm \pi}$![]() . Considering only the latter, we can translate $\theta$
. Considering only the latter, we can translate $\theta$![]() to $\theta + {\rm \pi}$
to $\theta + {\rm \pi}$![]() , making the two integrals have the same integration extreme. Since $\sin (\theta + {\rm \pi}) = - \sin \theta$
, making the two integrals have the same integration extreme. Since $\sin (\theta + {\rm \pi}) = - \sin \theta$![]() and $\cos (\theta + {\rm \pi}) = - \cos (\theta )$
and $\cos (\theta + {\rm \pi}) = - \cos (\theta )$![]() , the sign is absorbed in the denominator by the square, but it is left at the numerator, getting the wanted result.
, the sign is absorbed in the denominator by the square, but it is left at the numerator, getting the wanted result.
Appendix E. Boundary coefficients for convergence study
For the axisymmetric case, the boundary coefficients in figure 9 are $R_0^b = 1$![]() , $R_1^b = 0.6$
, $R_1^b = 0.6$![]() , $R_2^b = 0.8$
, $R_2^b = 0.8$![]() , $Z_0^b = 0$
, $Z_0^b = 0$![]() , $Z_1^b = 0.8$
, $Z_1^b = 0.8$![]() and $Z_2^b = 0.1$
and $Z_2^b = 0.1$![]() , with $N_{s} \times N_{\theta } = 1000 \times 1000$
, with $N_{s} \times N_{\theta } = 1000 \times 1000$![]() . The boundary coefficients for the non-axisymmetric domain are in table 1, where computations are performed with a grid of $N_{s} \times N_{\theta } \times N_{z} = 120 \times 120 \times 120$
. The boundary coefficients for the non-axisymmetric domain are in table 1, where computations are performed with a grid of $N_{s} \times N_{\theta } \times N_{z} = 120 \times 120 \times 120$![]() .
.
Table 1. The set of boundaries coefficients $R_{nm}^b$![]() and $Z_{nm}^b$
and $Z_{nm}^b$![]() with $N = 1$
with $N = 1$![]() and $M = 2$
and $M = 2$![]() .
.

Appendix F. Gradient of $\mathcal {S}$ in Zernike–Fourier space
in Zernike–Fourier space
The action gradient is given as

with $X_{pqr} = r_{pqr}, \, z_{pqr}$![]() . Its derivatives are given by
. Its derivatives are given by


with $\varTheta (x) = 0$![]() if $x < 0$
if $x < 0$![]() and $\varTheta (x) = 1$
and $\varTheta (x) = 1$![]() otherwise.
otherwise.