Chirped resonance dynamics in phase space

Abstract

The dynamics of passage and capture into resonance of a distribution of particles driven by a chirped frequency perturbation is discussed. The resonant capture in this case involves crossing of the separatrix by individual particles and, therefore, the adiabatic theorem cannot be used in studying this problem no matter how slow the variation of the driving frequency is. It is shown that, if instead of analysing complicated single particle dynamics in passage through resonance, one considers the slow evolution of a whole distribution of initial conditions in phase space, the adiabaticity and phase space incompressibility arguments yield a solution to the resonant passage problem. This approach is illustrated in the case of an ensemble of electrons driven by a chirped frequency wave passing through Cherenkov resonances with the velocity distribution of electrons.

1 Introduction

The passage through and capture into resonance in systems with slowly varying parameters is one of the outstanding problems of nonlinear physics. Examples include resonant capture in planetary dynamics (see Batygin 2015 and references therein), excitation of nonlinear waves (Friedland & Shagalov 2005; Barak et al. 2009), manipulation of trapped particle distributions for formation of antihydrogen (Andersen et al. 2010), resonant control of atomic and molecular systems (Karczmarek et al. 1999; Grosfeld & Friedland 2002; Marcus, Friedland & Zigler 2004) and more. The basic model of the passage through resonance is that of a particle of mass $m$ and charge $q$ in an anharmonic potential driven by a chirped frequency oscillating electric field. The Hamiltonian in this problem is

(1.1) $$\begin{eqnarray}H=\frac{1}{2m}p^{2}+qV(x)-\unicode[STIX]{x1D700}x\cos \unicode[STIX]{x1D711}_{d},\end{eqnarray}$$

where the driving force $\unicode[STIX]{x1D700}\cos \unicode[STIX]{x1D711}_{d}$ is viewed as a perturbation and the driving frequency $\text{d}\unicode[STIX]{x1D711}_{d}/\text{d}t=\unicode[STIX]{x1D714}_{d}(t)$ is a slow function of time passing through the resonance with the oscillator, which may or may not be excited initially. This problem is most conveniently analysed within the single resonance approximation (Chirikov 1979), which involves transformation from $p,x$ to action-angle variables $I,\unicode[STIX]{x1D703}$ of the unperturbed Hamiltonian $H_{0}=p^{2}/2m+qV(x)$ (so that $H_{0}=H_{0}(I)$ ) and yields the following system of evolution equations (Friedland 2008)

(1.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}I=-\unicode[STIX]{x1D700}a(I)\sin \unicode[STIX]{x1D6F7}, & \displaystyle\end{eqnarray}$$

(1.3) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6FA}(I)-\unicode[STIX]{x1D714}_{d}(t)-\unicode[STIX]{x1D700}\frac{\text{d}a}{\text{d}I}\cos \unicode[STIX]{x1D6F7}, & \displaystyle\end{eqnarray}$$

where we used Fourier expansion $x(I,\unicode[STIX]{x1D703})=\sum a_{n}(I)\exp (\text{i}n\unicode[STIX]{x1D703})$ and wrote the complex amplitude of the first harmonic as $a=a_{1}\exp (\text{i}\unicode[STIX]{x1D711})$ ; also $\unicode[STIX]{x1D6FA}(I)=\text{d}H_{0}/\text{d}I$ is the frequency of the oscillator and $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D703}-\unicode[STIX]{x1D711}_{d}+\unicode[STIX]{x1D711}_{1}$ is the phase mismatch between the oscillator and the drive. This system is governed by the single resonance Hamiltonian

(1.4) $$\begin{eqnarray}H_{r}=H_{0}(I)-\unicode[STIX]{x1D714}_{d}I-\unicode[STIX]{x1D700}a(I)\cos \unicode[STIX]{x1D6F7}.\end{eqnarray}$$

Hamiltonians of this type occur in many of the slow resonant problems mentioned above and have been studied in a variety of applications. The process of resonant capture in all these cases involves crossing of the separatrix and, therefore, the adiabatic theorem cannot be used in studying this crossing no matter how slow the variation of the driving frequency is. This complicates the theory and yields non-trivial solutions. For example, if the oscillator is excited initially, only a fraction of the possible initial conditions in phase space yield trapping of the oscillator in resonance followed by a continuing phase locking with the drive (autoresonance). The probabilistic approach in studying this case was pioneered by Neishtadt (1975) and later used in several applications (Neishtadt & Timofeev 1987; Neishtadt & Vasiliev 2005; Neishtadt, Vasiliev & Artemyev 2013). In contrast, if the oscillator starts in equilibrium, and the driving frequency passes its linear frequency, the capture into resonance and autoresonance in the system are guaranteed, provided the driving amplitude exceeds a threshold, scaling as $\unicode[STIX]{x1D6FC}^{3/4}$ with the chirp rate $\unicode[STIX]{x1D6FC}=|\text{d}\unicode[STIX]{x1D714}_{d}/\text{d}t|$ of the driving frequency (Fajans & Friedland 2001).

In the present work, we study the problem of passage through resonance with an ensemble of particles distributed in phase space. We show that, if instead of analysing complicated single orbit dynamics in passage through resonance (e.g. Neishtadt 1975; Timofeev 1978; Cary, Escande & Tennyson 1985; Dewar & Yap 2009) one considers the evolution of a continuous distribution of initial conditions in phase space, the adiabaticity of deeper trapped orbits and phase space incompressibility in the vicinity of the separatrix yield a solution to the resonant capture probability problem. Recently this approach was applied to the problem of capture of molecules into rotational resonance in an optical centrifuge (Armon & Friedland 2016), while here we illustrate these ideas in the case of a distribution of charged particles driven by a chirped frequency ponderomotive wave passing through the Cherenkov resonance with the distribution. The scope of the presentation will be as follows. Section 2 will describe our driven kinetic model, present numerical simulations and illustrate the complexity of passage through Cherenkov resonances. In § 3 we discuss our adiabatic phase space approach for calculating the resonant capture probability in the problem and compare the theory with simulation. The validity conditions of our theory will be discussed in § 4. Finally, § 5 will present our conclusions.

2 The distribution driven by a chirped frequency wave

Consider a one-dimensional problem of a tenuous electron distribution $f(v,x,t)$ driven by a travelling longitudinal field $E(t)\sin (kx-\int \unicode[STIX]{x1D714}_{d}\,\text{d}t)$ having slowly varying amplitude and frequency. Inclusion of the self-field of the distribution requires addition of the Poisson equation, the problem studied previously in application to Bernstein–Greene–Kruscal modes (Khain & Friedland 2010) and we will discuss the expected effect of this inclusion on the resonant capture probability in § 5. If one neglects the self-field, the single particle trajectory in this problem is governed by

(2.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}x=v, & \displaystyle\end{eqnarray}$$

(2.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}v=-\frac{e}{m}E(t)\sin \left(kx-\int \unicode[STIX]{x1D714}_{d}\,\text{d}t\right). & \displaystyle\end{eqnarray}$$

Therefore, defining $I=kv$ , $\unicode[STIX]{x1D6E9}=kx$ , $\unicode[STIX]{x1D6E9}_{d}=\int \unicode[STIX]{x1D714}_{d}\,\text{d}t$ , $\unicode[STIX]{x1D6F7}=\unicode[STIX]{x1D6E9}-\unicode[STIX]{x1D6E9}_{d}$ and $\unicode[STIX]{x1D700}=keE/m$ , we have

(2.3) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}I=-\unicode[STIX]{x1D700}(t)\sin \unicode[STIX]{x1D6F7}, & \displaystyle\end{eqnarray}$$

(2.4) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{t}\unicode[STIX]{x1D6F7}=I-\unicode[STIX]{x1D714}_{d}(t), & \displaystyle\end{eqnarray}$$

which is the same as (1.2) and (1.3) with $a=1$ , so our resonant Hamiltonian is

(2.5) $$\begin{eqnarray}H_{r}=H_{0}(I)-\unicode[STIX]{x1D714}_{d}(t)I-\unicode[STIX]{x1D700}(t)\cos \unicode[STIX]{x1D6F7},\end{eqnarray}$$

where $H_{0}(I)=I^{2}/2$ and $\unicode[STIX]{x1D6FA}=I$ . Remarkably, the same Hamiltonian describes the classical evolution of the angular momentum of a polar molecule (in the rigid rotor approximation) driven by an electric field rotating in the plane of molecular rotation (Marcus, Friedland & Zigler 2005). Therefore, our equations are isomorphic to those encountered in the problem of capture of an ensemble of molecules into a continuing rotational resonance, the configuration known as the optical centrifuge (Karczmarek et al. 1999).

We start our analysis by assuming a linear driving frequency chirp

(2.6) $$\begin{eqnarray}\unicode[STIX]{x1D714}_{d}=\unicode[STIX]{x1D714}_{0}+\unicode[STIX]{x1D6FC}t,\end{eqnarray}$$

where $\unicode[STIX]{x1D714}_{0}$ is the initial driving frequency. We introduce dimensionless time $\unicode[STIX]{x1D70F}=\sqrt{\unicode[STIX]{x1D6FC}}t$ and normalized $J=I/I_{c}$ , where $I_{c}$ is some characteristic value of $I$ . In these variables, the evolution equations (2.3) and (2.4) become

(2.7) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}J=-P_{1}\sin \unicode[STIX]{x1D6F7}, & \displaystyle\end{eqnarray}$$

(2.8) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F7}=P_{2}(J-J_{0})-\unicode[STIX]{x1D70F}, & \displaystyle\end{eqnarray}$$

where $J_{0}=\unicode[STIX]{x1D714}_{0}/I_{c}$ and the two dimensionless parameters are

(2.9a,b ) $$\begin{eqnarray}P_{1}=\frac{\unicode[STIX]{x1D700}}{I_{c}\sqrt{\unicode[STIX]{x1D6FC}}},\quad P_{2}=\frac{I_{c}}{\sqrt{\unicode[STIX]{x1D6FC}}}.\end{eqnarray}$$

These parameters can be associated with three characteristic time scales in the problem, i.e. the chirping time scale $T_{ch}=\unicode[STIX]{x1D6FC}^{-1/2}$ (this scale is only relevant in the chirp-driven problem), the time scale associated with the amplitude of the driving perturbation $T_{d}=I_{c}/\unicode[STIX]{x1D700}$ and the scale of the nonlinearity $T_{nl}=I_{c}^{-1}$ . In terms of these time scales, the two parameters in (2.7) and (2.8) are $P_{1}=T_{ch}/T_{d}$ and $P_{2}=T_{ch}/T_{nl}$ , referred to as the driving and nonlinearity parameters in the following. Note that the normalized driving frequency $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{d}/I_{c}$ can be written as $\unicode[STIX]{x1D714}=J_{0}+\unicode[STIX]{x1D70F}/P_{2}$ .

Figure 1. Passage through resonance with the cold beam distribution. (a) Initial distribution, (b) $P_{1}=0.1,P_{2}=30$ and (c) time varying $P_{1}$ case. The initial distribution is strongly perturbed, while 15.7 % of the particles are trapped in autoresonance with the drive for the time varying $P_{1}$ .

Next, we present the results of numerical simulations of our driven system for two initial particle distributions. Figure 1 illustrates the evolution of an initially monoenergetic particle beam $J=1$ at $\unicode[STIX]{x1D70F}=0$ with uniformly distributed values of $\unicode[STIX]{x1D6F7}$ , as shown in figure 1(a). Figure 1(b) shows the strongly perturbed distribution of these particles at $\unicode[STIX]{x1D70F}_{f}=60$ after passage through resonance (at $\unicode[STIX]{x1D70F}=15$ ) in the case of $P_{1}=0.1$ and $P_{2}=30.$ We choose the initial driving frequency $\unicode[STIX]{x1D714}(0)=J_{0}=0.5$ , so the final driving frequency is $\unicode[STIX]{x1D714}_{f}=2.5$ . Figure 1(c) shows the final distribution for the same parameters and initial conditions as in figure 1(a), but $P_{1}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70F}$ , $\unicode[STIX]{x1D6FD}=0.0067$ (note that at the time $\unicode[STIX]{x1D70F}=15$ of crossing of the resonance, in this case $P_{1}=0.1$ ). The final distribution in this case is also strongly perturbed but, in contrast to figure 1(b), 15.7 % of the initial distribution in figure 1(c) forms a separated region in phase space, which is trapped in resonance and enters the autoresonant stage as its averaged $\overline{J}$ is accelerated, following the driving frequency continuously $\overline{J}\approx 0.5+0.0067\unicode[STIX]{x1D70F}/P_{2}$ .

Figure 2. Passage through resonance with the water bag distribution. (a) Initial distribution, (b) $P_{1}=0.1,P_{2}=30$ and (c) time varying $P_{1}$ case. Only the boundaries of the initial distribution are perturbed after passage through resonance, while 11.8 % of the distribution is trapped in autoresonance with the drive for time varying $P_{1}$ .

Our second initial distribution, shown in figure 2(a), is uniform in $J$ between $J_{10}=1$ and $J_{20}=2$ and in $\unicode[STIX]{x1D6F7}$ , corresponding to the usual water bag model (Bertrand & Feix 1968; Berk, Nielsen & Roberts 1970). We again use $P_{2}=30$ , chirp the driving frequency as before by starting at $\unicode[STIX]{x1D714}(0)=0.5$ and allow it to cross the Cherenkov resonances with all the particles in the distribution at different times. The final distribution, after passage of $\unicode[STIX]{x1D714}$ through the distribution, in this case is shown for constant $P_{1}=0.1$ in figure 2(b) and increasing $P_{1}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70F}$ , $\unicode[STIX]{x1D6FD}=0.0067$ in figure 2(c). One can see in the figure that in both cases, after passage through the resonances, the distributions remained uniform except in the boundary regions and that the whole distribution is shifted on average to lower energies (the phenomenon discussed in Friedland, Khain & Shagalov (2006) and Schmit & Fisch (2012)). In addition, for the increasing $P_{1}$ case, some phase space area $\unicode[STIX]{x0394}S$ of the initial distribution is captured into resonance forming a ring of the same uniform initial density. This area is phase locked to the drive, continues its accelerating motion in $J$ as the driving frequency increases and defines the resonant capture probability $P=\unicode[STIX]{x0394}S/[2\unicode[STIX]{x03C0}(J_{20}-J_{10})]$ (in our example $P=11.8\,\%$ ). This capture probability is discussed next.

3 Resonant capture probability

Our theory below is based on analysing the dynamics governed by (2.7) and (2.8), which can be combined into a single second-order equation

(3.1) $$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}^{2}\unicode[STIX]{x1D6F7}=-D\sin \unicode[STIX]{x1D6F7}-1,\end{eqnarray}$$

where $D=P_{1}P_{2}$ . For constant $D$ , this equation describes a ‘pendulum’ subject to a constant ‘torque’ and is integrable. The pendulum moves in a tilted cosine potential

(3.2) $$\begin{eqnarray}V=\unicode[STIX]{x1D6F7}-D\cos \unicode[STIX]{x1D6F7}\end{eqnarray}$$

illustrated in figure 3(a). Figure 3(b) shows the phase space portrait of the dynamics. One can see that the phase space is divided into trapped and untrapped trajectories separated by the separatrix. The area of the separatrix in the $D=\text{const}$ case remains constant and all particles trapped inside the separatrix initially remain trapped at later times despite the variation of the driving frequency, while all the untrapped trajectories remain untrapped. Therefore, if the evolution of the separatrix starts in the empty region of phase space, its area will remain empty during the passage through the water bag distribution. The resonant capture probability in this case is zero, as seen in figure 2(b). Importantly, as the empty separatrix enters the distribution, it mainly disrupts the evolution of particles close to the separatrix, because other particles experience non-resonant forcing which effectively averages to zero. Therefore, in the water bag simulations in the constant $D$ case, we observe a significant disruption of the boundaries of the initial distribution, but as the separatrix enters the bulk of the distribution, the boundaries of the separatrix define a nearly empty hole surrounded by a uniform distribution having initial phase space density, because of the incompressibility of the phase space (Goldstein 1980). The situation changes drastically when the parameter $D$ varies (increases in our case) in time. We assume adiabatic variation of $D$ (see the discussion of this condition below), which conserves the actions (areas in phase space) associated with all trapped trajectories, but those in the vicinity of the separatrix. As the separatrix area grows, the phase space hole entering the water bag distribution from outside will remain mostly empty and preserves its area, while because of the incompressibility of the phase space fluid, the extension of the hole inside the growing separatrix will be filled by the particles having the initial phase space density. These trapped particles comprise the ring around the hole as seen in figure 2(c). Using these arguments and assuming that at all times the separatrix width $\unicode[STIX]{x0394}J$ in $J$ is small compared to the width of the initial distribution (this is our weak drive assumption, to be discussed in the next section), one can estimate the capture probability of newly trapped particles in the problem as

(3.3) $$\begin{eqnarray}Q=\frac{S_{out}-S_{in}}{2\unicode[STIX]{x03C0}(J_{20}-J_{10})},\end{eqnarray}$$

Figure 3. The effective potential equation (3.2) (a) for $P_{1}P_{2}=3$ and the phase space portrait of the associated dynamics (b). The boundary of the red filled area in the bottom panel is the separatrix. The equal energy lines in the bottom panel are separated by energy steps of $\unicode[STIX]{x03C0}$ .

where $S_{in}$ and $S_{out}$ are the instantaneous areas of the separatrix at the entrance and exit from the initial distribution. Here the area of the separatrix in ( $J,\unicode[STIX]{x1D6F7}$ ) phase space is

(3.4) $$\begin{eqnarray}S=\frac{1}{P_{2}}\oint \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F7}^{s}\,\text{d}\unicode[STIX]{x1D6F7},\end{eqnarray}$$

where $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F7}^{s}$ is the velocity of the ‘pendulum’ on the separatrix. The latter is found by observing that the energy at the separatrix is

(3.5) $$\begin{eqnarray}E^{\ast }=\unicode[STIX]{x1D6F7}^{\ast }-D\cos \unicode[STIX]{x1D6F7}^{\ast },\end{eqnarray}$$

where $\unicode[STIX]{x1D6F7}^{\ast }$ is the value of $\unicode[STIX]{x1D6F7}$ ( $\text{mod}(2\unicode[STIX]{x03C0})$ ) at the local maximum of the quasipotential (3.2) and that $\sin \unicode[STIX]{x1D6F7}^{\ast }=-1/D$ , $\cos \unicode[STIX]{x1D6F7}^{\ast }=-\sqrt{1-D^{-2}}$ . Then,

(3.6) $$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F7}^{s}=\pm \sqrt{2(E^{\ast }-\unicode[STIX]{x1D6F7}^{s}+D\cos \unicode[STIX]{x1D6F7}^{s})},\end{eqnarray}$$

or by using (3.5) and introducing $\unicode[STIX]{x1D717}=\unicode[STIX]{x1D6F7}^{s}-$ $\unicode[STIX]{x1D6F7}^{\ast }$ , we have

(3.7) $$\begin{eqnarray}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D717}=\pm \sqrt{2[\sin \unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}+A(1-\cos \unicode[STIX]{x1D717})]},\end{eqnarray}$$

where $A=(D^{2}-1)^{1/2}$ . Therefore, the area of the separatrix (3.4) can be evaluated from

(3.8) $$\begin{eqnarray}S=\frac{2\sqrt{2}}{P_{2}}\int _{0}^{2\unicode[STIX]{x03C0}}\text{Re}[\sin \unicode[STIX]{x1D717}-\unicode[STIX]{x1D717}+A(1-\cos \unicode[STIX]{x1D717})]^{1/2}\,\text{d}\unicode[STIX]{x1D717}.\end{eqnarray}$$

Figure 4. The rescaled area of the separatrix $P_{2}S$ versus parameter $D=P_{1}P_{2}$ (blue solid line) and its asymptotic value $16D^{1/2}$ (red dashed line).

We show $P_{2}S$ versus $D$ in figure 4. Note that no separatrix (trapped trajectories) exists if $D<1$ , $S$ is an increasing function of $P_{1}$ and asymptotically, as $D$ becomes large, $P_{2}S\rightarrow 16D^{1/2}$ . In the example in figure 2, (3.3) yields $Q=12.6\,\%$ , in good agreement with simulations. The developments above can be also used for calculating the trapping probability for resonant passage through an arbitrary initial distribution $F_{0}(J)$ (normalized as $\int F_{0}(J)\,\text{d}J=1/2\unicode[STIX]{x03C0}$ ). Indeed, define the resonant value $J_{r}$ , which follows the driving frequency continuously

(3.9) $$\begin{eqnarray}J_{r}(\unicode[STIX]{x1D70F})=J_{0}+\unicode[STIX]{x1D70F}/P_{2}.\end{eqnarray}$$

If the driving frequency increases during an infinitesimal time step $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F},$ then $J_{r}$ increases by $\unicode[STIX]{x1D6FF}J_{r}=\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D70F}/P_{2}$ and the separatrix area $S$ changes by $\unicode[STIX]{x1D6FF}S$ , the fraction of the trapped particles will change by

(3.10) $$\begin{eqnarray}F_{0}(J_{r})\unicode[STIX]{x1D6FF}S=F_{0}(J_{r})\frac{\text{d}S}{\text{d}J_{r}}\unicode[STIX]{x1D6FF}J_{r}.\end{eqnarray}$$

In all examples in this work, we assume that $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}P_{1}>0$ , so $\unicode[STIX]{x1D6FF}S>0$ and, therefore, (3.10) describes the fraction of newly trapped particles. Nevertheless, if the instantaneous $\text{d}S/\text{d}J_{r}$ is negative, i.e. $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}P_{1}<0$ , equation (3.10) describes the fraction of particles leaving the separatrix, i.e. detrap. By integration of (3.10), after a finite time, the trapping probability is

(3.11) $$\begin{eqnarray}Q=Q_{0}+\int _{J_{r}(\unicode[STIX]{x1D70F}_{1})}^{J_{r}(\unicode[STIX]{x1D70F}_{2})}F_{0}(J_{r})\frac{\text{d}S(J_{r})}{\text{d}J_{r}}\,\text{d}J_{r},\end{eqnarray}$$

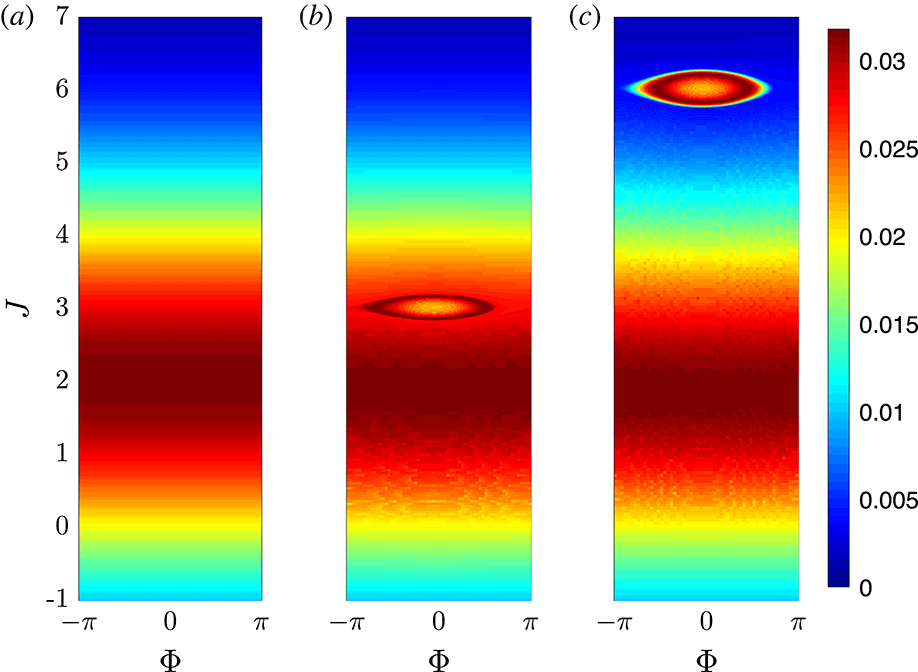
Figure 5. The chirp-driven phase space distribution at different times: (a) the initial shifted Gaussian distribution at $\unicode[STIX]{x1D70F}=0$ , (b) a resonant phase space hole in the distribution at $\unicode[STIX]{x1D70F}=90$ and (c) a resonant bump in the tail of the distribution at $\unicode[STIX]{x1D70F}=180$ . The colour coding represents probability density in phase space.

where $\unicode[STIX]{x1D70F}_{1}$ and $\unicode[STIX]{x1D70F}_{2}$ are the initial and final times, respectively, and $Q_{0}$ is the fraction of the particles inside the separatrix initially. For $\text{d}S/\text{d}J_{r}>0$ , this result can be interpreted probabilistically (Neishtadt 1975), viewing $(1/2\unicode[STIX]{x03C0})(\text{d}S(J_{r})/\text{d}J_{r})$ as the probability of resonant capture of uniformly distributed initial conditions in a thin strip in phase space of size $2\unicode[STIX]{x03C0}\,\text{d}J_{r}$ as the resonant action $J_{r}$ passes this strip. Note that (3.11) reduces to (3.3) in the water bag model, where $F_{0}(J)=1/(2\unicode[STIX]{x03C0}(J_{20}-J_{10}))$ for $J_{10}<J<J_{20}$ and zero elsewhere. As a more complex example, we consider a shifted Gaussian initial electron distribution, $F_{0}(J)=[4\unicode[STIX]{x03C0}\sqrt{2\unicode[STIX]{x03C0}}]^{-1}\exp [-(J-2)^{2}/8]$ . We again use parameters $P_{1}=\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D70F}$ , $\unicode[STIX]{x1D6FD}=0.0067,$ $P_{2}=30$ and show in figure 5 the distribution $F(J,\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D70F})$ at the initial, intermediate and final times of the simulation, as the driving frequency $\unicode[STIX]{x1D714}$ varies from 0 to 6. The formation of the resonant region inside the separatrix is seen in the figure, with colours indicating the origin in $J$ of different trapped particles. Additional information from this simulation is presented in figure 6, showing the distribution of the electrons in $J$ , i.e. $f(J,\unicode[STIX]{x1D70F})=\int F(J,\unicode[STIX]{x1D6F7},\unicode[STIX]{x1D70F})\,\text{d}\unicode[STIX]{x1D6F7}$ at times corresponding to those in figure 5. One can see the deviation of $f(J,\unicode[STIX]{x1D70F})$ from the initial distribution (dashed line) and the appearance of a resonant bump in the distribution which includes resonantly trapped particles. Finally, figure 7 compares the theoretical prediction (3.11) for the trapping probability $Q$ in this example for different initial driving frequencies $\unicode[STIX]{x1D714}(0)=J_{0}$ with simulations, showing a very good agreement.

Figure 6. The distribution $f(J,\unicode[STIX]{x1D70F})$ of the electrons (blue solid lines) at the times shown in figure 5. The initial distribution is shown by red dashed lines.

Figure 7. The resonant capture probability for initially Gaussian electron distribution versus initial resonant $J_{0}$ . The theoretical prediction is shown by the blue solid line, the yellow diamonds represent the results of the numerical simulations.

4 Validity conditions

We have made the adiabaticity and weak drive assumptions in developing the theory above and discuss these assumptions next. Both will be analysed in $D=P_{1}P_{2}\gg 1$ case (the width of the separatrix in $\unicode[STIX]{x1D6F7}$ in this case is nearly $2\unicode[STIX]{x03C0}$ ). In estimating the validity conditions of the theory we linearize equations (2.7), (2.8) in $\unicode[STIX]{x1D6F7}$

(4.1) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}(\unicode[STIX]{x1D6FF}J)=-P_{1}\unicode[STIX]{x1D6F7}, & \displaystyle\end{eqnarray}$$

(4.2) $$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D6F7}=P_{2}\unicode[STIX]{x1D6FF}J, & \displaystyle\end{eqnarray}$$

where $\unicode[STIX]{x1D6FF}J=J-J_{r}$ . The characteristic frequency of oscillations of $\unicode[STIX]{x1D6FF}J$ and $\unicode[STIX]{x1D6F7}$ in this system is $\unicode[STIX]{x1D708}=D^{1/2}$ . Then the adiabaticity condition for deeper trapped orbits is $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}\unicode[STIX]{x1D708}/\unicode[STIX]{x1D708}^{2}\ll 1$ , yielding (for $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D70F}}P_{1}=\unicode[STIX]{x1D6FD}$ )

(4.3) $$\begin{eqnarray}(P_{1}^{3}P_{2})^{1/2}\gg \unicode[STIX]{x1D6FD}.\end{eqnarray}$$

This condition preserves the area of the empty phase space hole inside the separatrix passing a water bag distribution, while the remaining area of the separatrix in this model is filled uniformly by trapped particles, as described above. Finally, we estimate the weak drive condition. The amplitude of oscillations of $\unicode[STIX]{x1D6FF}J$ is $\unicode[STIX]{x0394}J=P_{1}\unicode[STIX]{x0394}\unicode[STIX]{x1D6F7}/\unicode[STIX]{x1D708}$ . By using $\unicode[STIX]{x0394}\unicode[STIX]{x1D6F7}\sim O(1)$ and assuming $|J-J_{0}|\sim O(1)$ for typical values of $J$ in the distribution, the small $\unicode[STIX]{x0394}J$ (weak drive) condition $\unicode[STIX]{x0394}J\ll |J-J_{0}|$ can be written as

(4.4) $$\begin{eqnarray}(P_{1}/P_{2})^{1/2}\ll 1.\end{eqnarray}$$

The inequalities (4.3) and (4.4) in the trapping regime comprise the validity conditions of our theory and are satisfied in all our numerical examples. We illustrate these conditions in $P_{1,2}$ parameter space in figure 8. The condition $D=1$ (the separatrix exists for $D>1$ only) is also shown in the figure by dashed line. The region of the applicability of the theory is coloured in blue.

Figure 8. The region of validity of the theory in $P_{1,2}$ parameter space is coloured in blue. The black lines represent the weak drive and adiabaticity (for $\unicode[STIX]{x1D6FD}=2$ ) limits and the limit of the existence of the separatrix is shown by the dashed line.

5 Conclusions

In conclusion, we have studied the problem of capture of a distribution of electrons into a nonlinear resonance with a ponderomotive wave having a slowly chirped frequency. For individual particles, the theory of capture into resonance is complicated because of the non-adiabatic crossing of the separatrix between the trapped and untrapped trajectories. Nevertheless, if one considers the evolution of the whole distribution in phase space, the phase space incompressibility near the separatrix and adiabaticity of deeper trapped orbits still allow the calculation of the resonant capture probability, see (3.11). This result takes into account either resonant trapping or escape of the particles in passage through resonance depending on weather the area of the separatrix increases or decreases during the evolution. Furthermore, we have assumed a positive driving frequency chirp rate in the theory, but it can be easily reformulated to allow for a negative chirp rate. In all cases, the trapping probability is described by (3.11). Both the trapping and the escape from resonance, as well as down chirping of the driving frequency, are important in plasma applications (e.g. Ghizzo, Del Sarto & Reveille 2009). Our theory uses two dimensionless parameters $P_{1,2}$ (see (2.9)) related to three time scales in the problem characterizing the driving frequency variation, the driving strength and the nonlinearity, respectively. We have found the validity region of our formalism in the $P_{1,2}$ parameter space and compared the predictions of the theory with simulations, illustrating a good agreement. In addition to the problem analysed in this work, there exists many other important applications (e.g. passage through higher harmonic and subharmonic resonances and capture of molecules into rotational resonance (Armon & Friedland 2016)), where a similar analysis can be used in calculating the resonant capture efficiency. Finally, the inclusion of a self-field of the electrons in the resonant capture problem seems to be an important goal for future research. Such a theory would require a self-consistent analysis of the Vlasov–Poisson system. However, under certain conditions, the driven plasma wave phase locks to the driving wave (Khain & Friedland 2010). In this case, the resonant capture problem can be treated by adding the slowly varying amplitude of the excited plasma wave to that of the driving field, i.e. including this additional time variation in parameter $P_{1}$ .