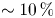1 Introduction
1.1 Motivation
Ultracold neutral plasmas (UNPs) (Killian et al. Reference Killian, Kulin, Bergeson, Orozco, Orzel and Rolston1999; Killian Reference Killian2007) have several properties that make them excellent systems in which to study fundamental plasma properties. Their cold and tuneable temperatures, dilute and adjustable densities, and known ionization states mean that UNPs are very classical (i.e. quantum effects are expected to be very small), their dynamics have time scales that are accessible to conventional electronics, they do not have detectable collisions with neutral atoms, their ions and electrons can have an adjustable amount of strong coupling (Ichimaru Reference Ichimaru1982; Lyon & Bergeson Reference Lyon and Bergeson2015; Chen, Witte & Roberts Reference Chen, Witte and Roberts2017; Langin, Gorman & Killian Reference Langin, Gorman and Killian2019) and because of their cold temperatures they can be strongly magnetized at easily accessible laboratory magnetic fields (Baalrud & Daligault Reference Baalrud and Daligault2017; Sprenkle et al. Reference Sprenkle, Bergeson, Silvestri and Murillo2022). Through scaling relations, the experimentally measured or theoretically determined properties of UNPs can be related to more complicated plasmas at higher temperatures and densities (Bergeson et al. Reference Bergeson, Baalrud, Ellison, Grant, Graziani, Killian, Murillo, Roberts and Stanton2019), including plasmas used for fusion (Betti & Hurricane Reference Betti and Hurricane1999), having conditions like those of fusion plasmas (Frenje et al. Reference Frenje, Grabowski, Li, Seguin, Zylstra, Johnson, Petrasso, Glebov and Sangster2015) and dense astrophysical plasmas (Paquette et al. Reference Paquette, Pelletier, Fontaine and Michaud1986; van Horn Reference van Horn1991; Paxton et al. Reference Paxton, Marchant, Schwab, Bauer, Bildsten, Cantiello, Dessart, Farmer, Hu and Langer2015). In this way, UNPs are similar to non-neutral plasmas that are also well-suited to studies of fundamental plasma physics (Dubin & O'Neil Reference Dubin and O'Neil1999).
In order to have the widest range of possible experimental measurements of UNPs, development of new diagnostic techniques is needed. This article describes a technique for measuring the electron temperature heating rate caused by an externally applied field. This technique uses a sequence of time-varying applied direct-current (DC) electric fields: to prepare the UNP for application of the heating field; to provide time for the heating and the electrons to come to thermal equilibrium afterward; to extract a fraction of the UNP electrons towards a detector in a temperature-sensitive way; and to extract the remaining electrons to measure the total electron number in the UNP. The method and details associated with this technique are presented throughout the rest of this article.
As an example of how this technique can be used, electron heating by radiofrequency (RF) fields is measured (Porkolab Reference Porkolab2007). Measuring the RF heating rate experimentally determines the absorptive part of the alternating-current (AC) conductivity of the UNP, so this technique can be used to measure the variation of that quantity as a function of plasma parameters. We are particularly interested in measuring this as a function of electron magnetization (Oberman & Shure Reference Oberman and Shure1963; Chen Reference Chen1974; Matsuda Reference Matsuda1981; Guthrie & Roberts Reference Guthrie and Roberts2021).
There are several existing diagnostic techniques for UNPs. Light (Cummings et al. Reference Cummings, Daily, Durfee and Bergeson2005; Castro, Gao & Killian Reference Castro, Gao and Killian2008) and charge (Zhang, Fletcher & Rolston Reference Zhang, Fletcher and Rolston2009; Schulz-Weiling & Grant Reference Schulz-Weiling and Grant2016; Kroker et al. Reference Kroker, Grossmann, Sengstock, Drescher, Wessels-Staarmann and Simonet2021) imaging methods can be used to measure the ion component's spatial extent and velocities. But, these techniques do not extend to the electron component. Instead, the electron component of UNPs is measured through the electron escape rate from the UNP (Killian et al. Reference Killian, Kulin, Bergeson, Orozco, Orzel and Rolston1999; Roberts et al. Reference Roberts, Fertig, Lim and Rolston2004) or the fields produced as the electrons oscillate in response to applied RF fields (Twedt & Rolston Reference Twedt and Rolston2012). Additionally, the UNP expansion rate can be used to determine the electron temperature (Kulin et al. Reference Kulin, Killian, Bergeson and Rolston2000; Gupta et al. Reference Gupta, Laha, Simien, Gao, Castro, Killian and Pohl2007). In each of these techniques, measuring electron heating present only for a short time, like that from an RF heating pulse, requires reliance on models to interpret the data, or deriving the short-time heating amount from signals integrated over a much longer period of time, or both. The electron heating measurement technique presented in this article does not rely on modelling and requires only enough time for electrons to thermalize in order to perform the measurement.
In order to place this technique in context, UNP formation and evolution will be briefly described. The heating measurement technique will then be presented in detail along with the calibrations that are needed to interpret the measurements and relate them to theoretical predictions. Particular attention will be paid to measuring high-frequency AC conductivity in UNPs. Finally, possible improvements will be described.
1.2 Introduction to UNPs
A UNP is formed through the photoionization of a finite-spatial-extent gas of laser-cooled atoms (Killian et al. Reference Killian, Kulin, Bergeson, Orozco, Orzel and Rolston1999) or photoionization of either atoms (Heilmann, Peatross & Bergeson Reference Heilmann, Peatross and Bergeson2012) or molecules (Morrison et al. Reference Morrison, Rennick, Keller and Grant2008) in a supersonic beam. The UNPs can also be formed from avalanche ionization of Rydberg gases (Robinson et al. Reference Robinson, Tolra, Noel, Gallagher and Pillet2000). The wavelength of the photoionization laser is tuneable, so the initial average electron kinetic energy and thus temperature can be controlled. The number of electrons and ions are initially equal when the neutral atom cloud is photoionized, After photoionization, some electrons escape the UNP region since they have non-zero kinetic energy. As electrons escape, however, a space charge develops owing to the more massive, positively charged ions in the UNP. This space charge eventually becomes large enough to confine the remaining electrons. The electrons and ions then come to thermal equilibrium with themselves but not with each other and a two-component electron and ion plasma is formed. Since the ions are unconfined, the UNP eventually expands (Kulin et al. Reference Kulin, Killian, Bergeson and Rolston2000; Robicheaux & Hanson Reference Robicheaux and Hanson2002), but the work described in this article occurs before the expansion is significant. As a result, the ion number does not change during the experiments conducted with the exception of three-body recombination (Robicheaux & Hanson Reference Robicheaux and Hanson2002; Tiwari & Baalrud Reference Tiwari and Baalrud2018), which is minimal for the conditions presented in this work.
The electron escape rate can be modified by applying an external electric field that alters the potential well formed by the space charge. A sufficiently strong applied electric field can induce electrons to escape (Roberts et al. Reference Roberts, Fertig, Lim and Rolston2004), forming the basis of the critical part of our heating rate measurement technique. In response to a reduction in the confining potential, electrons will leave until a space charge once again restricts this loss. The higher the electron temperature, the more electron escape is needed to confine the higher temperature electrons and the larger the number of electrons that escape in response to the applied electric field. So, the electron escape number depends on the electron temperature and can be used as a probe of that temperature.
1.3 Overview of the electron heating measurement technique
In this section, an overview of our technique to measure electron heating rates in UNPs is presented, and the details of all of the components of the technique are described in later sections of this article.
At the core of the measurement technique is the fact that externally applied DC electric fields can be used to extract electrons from a UNP to both control the net charge of the UNP and produce a signal sensitive to electron temperature (Roberts et al. Reference Roberts, Fertig, Lim and Rolston2004). In the absence of an externally applied DC electric field, the electrons are confined in the UNP by a potential formed by the excess positive charge arising from the fact that there are more ions in the UNP than electrons after some electrons escape shortly after formation. Applying an external DC electric field reduces the confinement of this potential along one direction, allowing electrons to escape. The number of electrons that escape is determined by electron temperature and charge balance considerations (i.e. enough electrons have to escape so that a sufficiently confining potential is restored).
As part of our method to measure an electron heating rate, the strength of an applied DC electric field is varied as a function of time after UNP creation in four phases of a measurement sequence. In the first phase, an applied DC electric field is slowly linearly increased as a function of time and then decreased in a ‘triangle ramp’ with the purpose of removing electrons from the UNP while otherwise minimally disturbing it. This creates a deeper confining potential for the next phase. In the second phase, either no or at most a small DC electric field is applied such that no electrons escape from the UNP. During this second phase, which we call the ‘testing phase’, electron heating can be induced using multiple methods that include RF heating or a short electric field pulse. The heating is applied only at the start of the testing phase, and the phase is made long enough that the heat fully thermalizes so that the electrons achieve thermal equilibrium at a higher temperature.
In the third phase, a DC electric field is applied at a selected strength that allows approximately 10 % of the electrons to escape. The number of electrons that escape is a function in part of the electron temperature (Roberts et al. Reference Roberts, Fertig, Lim and Rolston2004; Twedt & Rolston Reference Twedt and Rolston2010; Wilson, Chen & Roberts Reference Wilson, Chen and Roberts2013b). In principle, a model or theory could be used to link the electron escape in this phase to the electron temperature. The temperature-sensitive part of the signal is only approximately 10 %–15 % of the escape signal, though, so 1 %–1.5 % of the total electron number. Several auxiliary measurements would be needed to both use and validate any such model. Instead, our heating measurements rely on finding heating parameters for two different heating methods such that the amount of heating is matched between the two methods, resulting in the same electron escape fraction during phase three for each method. One of the two methods is calibrated to a known temperature increase, allowing a heating rate measurement of the other method (e.g. an RF heating rate). Since the electrons are in thermal equilibrium prior to phase three, if the electron escape number is the same and the other UNP parameters are the same, then the heating induced by the two methods is the same.
In the fourth phase, the DC electric field is increased to a strong enough value to remove all the electrons from the UNP. This is used to measure the total electron number and ion number since the total electron and ion numbers are equal. The total number is used in the characterization and analysis of the electron heating measurements. Figure 1 illustrates the time sequence of the applied electric field along with depicting heating pulses that can be applied during the second phase. There are several types of measurements that need to be made in order for this technique to produce data that can be compared with theoretical predictions. The UNP density must be known. That can be measured through resonant RF excitation of electron oscillations since the resonant frequency is density dependent. The electron temperature at the start of the testing phase needs to be known so that theory comparisons are possible. This is accomplished through choosing parameters such that the electron temperature is determined almost solely by photoionization laser wavelengths that can in turn be calibrated. Small corrections from the first phase's triangle ramp, stray electric fields (Jiang & Roberts Reference Jiang and Roberts2019) and other effects are determined through numerical modelling of the UNP conditions.

Figure 1. Sequence of applied electric fields for a heating measurement. The orange line shows the DC field that is applied to the UNPs. The increase in field just after $6\,\mathrm {\mu }{\rm s}$![]() is the field that partially extracts electrons to obtain the electron-temperature-sensitive electron escape signal. The final larger electric field increase is designed to extract all of the electrons from the plasma to measure the total electron number. Heating fields are shown in blue. In panel (a), RF heating via a 60 MHz applied RF field is shown. In panel (b), an impulse ‘kick’ field is shown (see text in § 2.3 for details). In all cases, the applied fields are shown to scale. The time $t=0$
is the field that partially extracts electrons to obtain the electron-temperature-sensitive electron escape signal. The final larger electric field increase is designed to extract all of the electrons from the plasma to measure the total electron number. Heating fields are shown in blue. In panel (a), RF heating via a 60 MHz applied RF field is shown. In panel (b), an impulse ‘kick’ field is shown (see text in § 2.3 for details). In all cases, the applied fields are shown to scale. The time $t=0$![]() corresponds to when the UNP is formed.
corresponds to when the UNP is formed.
Deliberate changes in the photoionization laser wavelength and thus electron photoionization energy are used to link a measured change in the third phase's integrated electron escape signal to a known change in electron temperature. This is the original calibrated heating method that is used as a comparison with other heating methods. For technical reasons described in the following sections, it is inconvenient to use this photoionization energy-based method as one of the two methods for directly comparing measured heating rates, so an impulse-heating-based method calibrated to the photoionization energy was developed. In this method, a short electric field pulse, which we call a ‘kick’, is applied to the UNP. The kick induces a free electron oscillation that eventually damps and has its associated kinetic energy turn into heat through electron–ion and electron–electron collisions. The kick produces a consistent amount of heating across plasma conditions. So once it is calibrated to the photoionization energy-based method, it can in turn be used as the calibrated heating method to measure other heating rates.
In this article, we describe the measurement of a particular heating mechanism as an example of the utility of this measurement technique. We measure electron heating from high-frequency RF applied to the UNP. The amplitude of the RF field is adjusted to find the amplitude where the RF heating matches that from the kick pulse for a chosen set of UNP conditions. Since the electron kick heating amount is calibrated to a known temperature rise, this links an experimental-unit RF amplitude (i.e. a voltage on a function generator) to a specific amount of electron heating. For any measurements of relative RF heating rates across different UNP conditions, this would be sufficient.
It is also possible to obtain an absolute calibration of the RF amplitude with additional measurements. When measuring the RF heating rate, the RF amplitude is turned on and off slowly enough that after the RF has been applied no residual electron centre-of-mass motion remains. If instead the RF is turned off quickly, there is residual electron centre-of-mass motion and the electrons oscillate around the position of the ions. As with kick pulses, this oscillation damps and its energy is converted into an increase in the electron temperature. This electron oscillation amplitude and therefore heating is related to the electric field amplitude of the RF at the location of the UNP. By matching the amount of heating between RF that is turned off slowly and turned off quickly, the RF electric field amplitude can be determined. Doing so requires knowledge of the electrical response of the experimental apparatus to sudden changes in RF field amplitude, and auxiliary measurements are performed in order to determine the relevant parameters.
The final result is a measurement of the absorptive part of the AC conductivity of a UNP for a chosen set of UNP and applied RF conditions: density, electron temperature, applied magnetic field and RF frequency. We report such an AC conductivity value along with the associated statistical and systematic uncertainties. A summary of the types of measurements that were required to determine the AC conductivity is presented in table 1.
Table 1. Required measurements for the heating measurement technique with brief descriptions and section locations.

2 The UNP formation and electron extraction
2.1 The UNP creation and escaping electron detection
The typical sequence we use to generate UNPs and our primary diagnostic signal are presented in this section. A cloud of $^{85}$![]() Rb is trapped and cooled in a magneto-optical trap (MOT) (Chu Reference Chu1998; Cohen-Tannoudji Reference Cohen-Tannoudji1998; Phillips Reference Phillips1998) loaded from background vapour in a glass cell. Following compression (Petrich et al. Reference Petrich, Anderson, Ensher and Cornell1994) and polarization gradient cooling (Dalibard & Cohen-Tannoudji Reference Dalibard and Cohen-Tannoudji1989) stages, atoms are loaded from the MOT into a magnetic quadrupole trap generated by anti-Helmholtz (AH) coils mounted on a translation stage (Lewandowski et al. Reference Lewandowski, Harber, Whitaker and Cornell2003). The neutral atoms are transported 73 cm from the MOT region to the photoionization region by moving the trapping coils along the length of a stainless steel vacuum chamber; see figure 2 for a diagram of the apparatus. Optical access allows the atom cloud to be photoionized via a two-photon process using 780 and 479 nm lasers (Wilson, Chen & Roberts Reference Wilson, Chen and Roberts2013a). This moment marks the formation of the UNP. A typical photoionization sequence used in the work described in this article produces a plasma with an electron and ion number of the order of $10^5$
Rb is trapped and cooled in a magneto-optical trap (MOT) (Chu Reference Chu1998; Cohen-Tannoudji Reference Cohen-Tannoudji1998; Phillips Reference Phillips1998) loaded from background vapour in a glass cell. Following compression (Petrich et al. Reference Petrich, Anderson, Ensher and Cornell1994) and polarization gradient cooling (Dalibard & Cohen-Tannoudji Reference Dalibard and Cohen-Tannoudji1989) stages, atoms are loaded from the MOT into a magnetic quadrupole trap generated by anti-Helmholtz (AH) coils mounted on a translation stage (Lewandowski et al. Reference Lewandowski, Harber, Whitaker and Cornell2003). The neutral atoms are transported 73 cm from the MOT region to the photoionization region by moving the trapping coils along the length of a stainless steel vacuum chamber; see figure 2 for a diagram of the apparatus. Optical access allows the atom cloud to be photoionized via a two-photon process using 780 and 479 nm lasers (Wilson, Chen & Roberts Reference Wilson, Chen and Roberts2013a). This moment marks the formation of the UNP. A typical photoionization sequence used in the work described in this article produces a plasma with an electron and ion number of the order of $10^5$![]() –$10^6$
–$10^6$![]() and density of the order of $10^7\,\mathrm {cm}^{-3}$
and density of the order of $10^7\,\mathrm {cm}^{-3}$![]() . The electron temperature can be tuned from $T_{e} \approx 1.5\unicode{x2013}6$
. The electron temperature can be tuned from $T_{e} \approx 1.5\unicode{x2013}6$![]() K for these measurements through tuning the energy imparted during photoionization. Additional details about setting and determining the electron temperature are presented in § 3.5. The ion temperatures are not measured in our experiments. Following other work (Langin et al. Reference Langin, Strickler, Maksimovic, McQuillen, Pohl, Vrinceanu and Killian2016), we estimate the temperature of the ions to be $T_{i} \lessapprox 0.3\,\mathrm {K}$
K for these measurements through tuning the energy imparted during photoionization. Additional details about setting and determining the electron temperature are presented in § 3.5. The ion temperatures are not measured in our experiments. Following other work (Langin et al. Reference Langin, Strickler, Maksimovic, McQuillen, Pohl, Vrinceanu and Killian2016), we estimate the temperature of the ions to be $T_{i} \lessapprox 0.3\,\mathrm {K}$![]() .
.

Figure 2. Diagram of the experimental apparatus. The $^{85}$![]() Rb atoms are laser cooled and trapped in the neutral region. They are then transferred to a purely magnetic trap which in turn is physically transported 73 cm to the centre of the four-way cross where the UNP is formed. Ports that provide optical access, ports to the ion pumps, the MCP detector (see text) and the location of electrodes and wire grids are shown. This figure is not to scale.
Rb atoms are laser cooled and trapped in the neutral region. They are then transferred to a purely magnetic trap which in turn is physically transported 73 cm to the centre of the four-way cross where the UNP is formed. Ports that provide optical access, ports to the ion pumps, the MCP detector (see text) and the location of electrodes and wire grids are shown. This figure is not to scale.
A series of positively charged wire grids in the vacuum chamber pulls electrons that escape the plasma towards a microchannel plate detector (MCP). The escaping electron current is detected by the MCP. The MCP output is stored on a gigahertz oscilloscope for analysis; see figure 3 for a diagram of the electrodes and wire grids that surround the UNP. The MCP current is the primary signal used to measure and characterize the plasma. Electrodes in the plasma region also let us apply DC and RF electric fields. A coil wrapped around the outside of the vacuum chamber allows the application of a magnetic field to the plasma of up to $100\,\mathrm {mT}$![]() directed along the axis of the vacuum system. The two closest electrodes to the UNP are a copper disk with a hole in the centre to allow ultracold atoms transported from the neutral region to pass through and a wire grid on the MCP side of the chamber.
directed along the axis of the vacuum system. The two closest electrodes to the UNP are a copper disk with a hole in the centre to allow ultracold atoms transported from the neutral region to pass through and a wire grid on the MCP side of the chamber.

Figure 3. Cross-sectional diagram of the electrodes and conducting surfaces nearest the UNP region of the vacuum system. Neutral atoms come from the left through the hole in the copper disk to the photoionization region where the UNP is created. Both DC and RF voltages can be applied to the copper disk. Time-varying voltages can be applied to the wire grid to apply chosen DC electric fields to the UNP and to extract electrons towards the detector. All grids and electrodes are enclosed in an aluminium tube to prevent fields from the insulated wires interfering with the UNP and the electron extraction. For clarity, a coil which is used to produce an axial magnetic field is not shown in this figure. This coil consists of 120 turns of magnet wire and produces a magnetic field directed to the right at the location of the plasma. The centre of this coil is aligned with the photoionization volume. Additionally, optical access ports in the aluminium tube are not shown in the figure.
The primary limitations to the data collection rate are the time it takes to fill the MOT, the time that it takes to transport the atoms from the MOT to the photoionization region, and the time needed to periodically relock the cooling lasers to the proper frequencies. We lock our cooling lasers with wide-recapture-range dichroic atomic vapour laser locks (Corwin et al. Reference Corwin, Lu, Hand, Epstein and Wieman1998) to enhance their ability to remain locked even in the presence of substantial electronic noise from rapidly changing currents associated with magnetic field production and laser flashlamp discharges. Despite this, the significant electronic transients generated during the UNP formation will occasionally cause the lasers to become unlocked, and a locking procedure is needed to relock them. Temperature drifts in the laboratory will also create a need for laser relocking once every several to tens of minutes. The MOT fill, transport, and relocking procedure times are all of the order of tens of seconds with the MOT fill time being approximately one minute and the relock time exceeding that (but not necessary on every shot). Not every shot is successful, so it typically takes 3–4 hr to collect 100 individual shots.
2.2 Numerical simulation methods
Before proceeding further with the description of our experimental technique, it is useful to describe two numerical simulation methods that we have developed. These simulations are used to test assumptions that we employ in our experimental design and data analysis. In addition, they are used to determine parameters needed for interpretation of our data.
Numerical simulation of plasmas has a well-known complication due to the long-range nature of the Coulomb force. For $N$![]() plasma particles, the most straightforward calculation of the acceleration of each particle in a time step in a simulation requires $O(N^2)$
plasma particles, the most straightforward calculation of the acceleration of each particle in a time step in a simulation requires $O(N^2)$![]() calculations. Given that $N$
calculations. Given that $N$![]() is of the order of $10^5$
is of the order of $10^5$![]() in our plasmas, this presents a computational challenge. Techniques exist that reduce this $N$
in our plasmas, this presents a computational challenge. Techniques exist that reduce this $N$![]() scaling to $O(N)$
scaling to $O(N)$![]() (Kudin & Scuseria Reference Kudin and Scuseria1998; Dharuman et al. Reference Dharuman, Stanton, Glosli and Murillo2017), but instead we rely on parallel processing and a hardware solution to the computational problem. The $N^2$
(Kudin & Scuseria Reference Kudin and Scuseria1998; Dharuman et al. Reference Dharuman, Stanton, Glosli and Murillo2017), but instead we rely on parallel processing and a hardware solution to the computational problem. The $N^2$![]() forces in a time step can be computed in parallel using a graphics processing unit (GPU), resulting in computational speeds 1000 or more times faster than a single central processing unit (CPU) and acceptable simulation runtimes (Witte Reference Witte2017). A constant softening parameter $\alpha$
forces in a time step can be computed in parallel using a graphics processing unit (GPU), resulting in computational speeds 1000 or more times faster than a single central processing unit (CPU) and acceptable simulation runtimes (Witte Reference Witte2017). A constant softening parameter $\alpha$![]() is added to the Coulomb potential between particles such that the pairwise interaction potential that is used in the simulation is $U={q_1 q_2}/({4 {\rm \pi}\epsilon _0 \sqrt {r^2+\alpha ^2}})$
is added to the Coulomb potential between particles such that the pairwise interaction potential that is used in the simulation is $U={q_1 q_2}/({4 {\rm \pi}\epsilon _0 \sqrt {r^2+\alpha ^2}})$![]() where $q_i$
where $q_i$![]() is the particle charge and $r$
is the particle charge and $r$![]() the distance between the two charges. This is done to avoid numerical errors associated with the fact that both positive and negative charges are present in our plasmas (Tiwari & Baalrud Reference Tiwari and Baalrud2018).
the distance between the two charges. This is done to avoid numerical errors associated with the fact that both positive and negative charges are present in our plasmas (Tiwari & Baalrud Reference Tiwari and Baalrud2018).
The first type of simulation we use is a molecular-dynamics (MD) simulation where all ions and electrons are treated as individual Coulomb-force-interacting classical particles whose motion is computed using the Boris algorithm (Boris & Shanny Reference Boris and Shanny1972). This simulation is useful in testing the significance of heating from three-body recombination (Robicheaux & Hanson Reference Robicheaux and Hanson2002; Tiwari & Baalrud Reference Tiwari and Baalrud2018) or stray/applied electric fields (Jiang & Roberts Reference Jiang and Roberts2019) for our experimental conditions.
The second type of simulation that was used more frequently we call a Monte Carlo (MC) simulation. All the electrons are still simulated as point particles. The ions, however, are replaced with a smooth average charge distribution and an electron–ion collision probability for each electron in each time step. If a collision occurs, a random impact parameter is selected and Rutherford scattering is used to compute the deflection angle of the electron velocity. For the MC simulations that are used to test experimental assumptions or derive experimental parameters, the exact value of the collision rate is not significant and tests are conducted to confirm that is the case. The usefulness of the MC simulations is that the electron–ion collision rate can be increased or decreased to test assumptions and that the MC simulations are faster than the MD simulations. These simulations were used to ensure that for our parameters any RF heating was overwhelmingly due to electron–ion collisions (as opposed to having a contribution from electron–electron collisions or some other source) and to calibrate the plasma spatial size given measurements of the resonant response of the electrons to an applied RF field (see § 3.1).
In the following sections, reference to both of these simulation methods will be made when they were used to test assumptions or support the determination of experimental parameters.
2.3 Electron-temperature-sensitive extraction
To perform our heating measurements (Guthrie Reference Guthrie2021), we use the applied DC electric field sequence shown in figure 1. This electric field is created by applying a voltage to the wire grid closest to the UNP. The MCP traces that are recorded from this sequence with and without applied heating are shown in figure 4.

Figure 4. The MCP traces demonstrating electron extraction signal sensitivity to heating. The set of traces in (a) show the data from the full sequence while the set of traces in (b) show only the time from approximately 6.5–9.5 $\mathrm {\mu }{\rm s}$![]() . The applied electric field sequence used in the collection of this data is shown in figure 1. The blue trace is without any RF heating, while the orange trace had an RF heating pulse applied for $1.2\,\mathrm {\mu }{\rm s}$
. The applied electric field sequence used in the collection of this data is shown in figure 1. The blue trace is without any RF heating, while the orange trace had an RF heating pulse applied for $1.2\,\mathrm {\mu }{\rm s}$![]() after the space charge adjustment was completed (see figure 1a). Each of the traces shown is the average of 100 individual measurements. The traces in (b) show the signal that is integrated to determine the electron number extracted, which we refer to as the PEF (see main text). It is clear that applying RF heating to the plasma increases the PEF.
after the space charge adjustment was completed (see figure 1a). Each of the traces shown is the average of 100 individual measurements. The traces in (b) show the signal that is integrated to determine the electron number extracted, which we refer to as the PEF (see main text). It is clear that applying RF heating to the plasma increases the PEF.
The first triangle-shaped field sequence is used to extract electrons from the plasma to increase the space charge of the plasma region. It is slow enough that the electron temperature is not affected substantially. The increase in space charge caused by removing electrons creates a deep potential well for the remaining electrons, preventing any electron escape and ensuring any energy imparted during heating stays within the UNP.
There is then a ‘testing phase’ of several microseconds of no applied field from the wire grid. It is during this time that RF or other electric field sequences can be applied, usually during the early part of this phase. During this phase, the electrons are given time to come into thermal equilibrium after any heating has been applied.
Next, the electric field is increased to a chosen value in 200 ns that extracts 10 %–15 % of the electrons from the UNP. We term the fraction of electrons extracted in this step as the ‘partial electron fraction (PEF)’. The PEF is calculated by integrating the electron signal on the MCP that results from the DC field applied during this phase. Most of the electron escape in the PEF can be attributed to plasma charge balance requirements. Enough electrons have to leave the UNP that the net potential formed by the UNP space charge and the applied electric field is confining in all directions. In addition to this charge balancing requirement, there is part of the electron escape signal that is sensitive to the electron temperature. Higher electron temperature leads to a larger PEF. This temperature sensitivity makes the PEF the main quantity of interest in our heating measurements.
At the end of the sequence, a much larger electric field is applied to remove all of the remaining electrons from the UNP. This provides a measurement of the total number of electrons that were in the UNP. Because there is one ion for every electron when the UNP is produced, determining the total electron number also determines the UNP ion number. This total number determination could in principle be complicated by Rydberg atom formation after the UNP is created since an ion and electron would be removed from the plasma. Explicit measurements of the Rydberg fraction in the UNP were performed via field ionization, and the measured fraction was consistent with zero with an uncertainty of 0.3 %. This is reasonable given that the predicted fraction of ions that are converted to Rydberg atoms is $3.8\times 10^{-4} \,\mathrm {\mu } {\rm s}^{-1}$![]() (Pohl, Vrinceanu & Sadeghpour Reference Pohl, Vrinceanu and Sadeghpour2008), using the definition of Rydberg atoms in that reference (namely atoms bound by 4$k_B T_e$
(Pohl, Vrinceanu & Sadeghpour Reference Pohl, Vrinceanu and Sadeghpour2008), using the definition of Rydberg atoms in that reference (namely atoms bound by 4$k_B T_e$![]() or more). In addition, magnetic fields typically used in these experiments are expected to reduce this rate further (Tiwari & Baalrud Reference Tiwari and Baalrud2018). We note that our experimental measurement was sensitive to more loosely bound atoms as well as those defined as Rydberg atoms in Pohl et al. (Reference Pohl, Vrinceanu and Sadeghpour2008).
or more). In addition, magnetic fields typically used in these experiments are expected to reduce this rate further (Tiwari & Baalrud Reference Tiwari and Baalrud2018). We note that our experimental measurement was sensitive to more loosely bound atoms as well as those defined as Rydberg atoms in Pohl et al. (Reference Pohl, Vrinceanu and Sadeghpour2008).
Due to the difficulties in directly measuring the temperature rise from the PEF signal presented in § 1.3 above, measurements are made by heating the UNP with two different methods and then finding the parameters for which both methods induce the same amount of heat. One of these two is the method being experimentally investigated while the other is calibrated to a known temperature rise to provide a benchmark for the quantity being tested. As long as the charge imbalance is the same, the two methods have the same total electron heating when the PEF is the same. If necessary, the charge imbalance can be adjusted with the first triangle ramp of the DC electric field sequence. The details of how this matching is performed are discussed in the context of necessary calibrations and the measurement method for RF heating rates discussed in the following sections.
3 Calibrated heating methods, density and temperature calibrations and uncertainty reduction techniques
3.1 Density calibration
The density of the UNP (Kulin et al. Reference Kulin, Killian, Bergeson and Rolston2000; Wilson et al. Reference Wilson, Chen and Roberts2013a) is an important parameter needed for the interpretation of experimental results. Many forms of heating have a density dependence, so comparisons with predictions require knowing the UNP density. The density is also an important parameter needed for simulating UNPs that match those produced experimentally.
If the electrons in the UNP are displaced from the centre of the ion spatial distribution, there will be a restoring force acting on them that is proportional to the density. Therefore, the resulting electron centre-of-mass oscillation has a density-dependent frequency (Wilson et al. Reference Wilson, Chen and Roberts2013a). The density is a function of the spatial size of the ultracold atoms before photoionization and the number of electrons and ions formed via photoionization. That number can be controlled by adjusting the 780 nm laser intensity in the two-step photoionization process. Setting the density of the UNP to a desired value involves determining the electron (and thus ion) number that produces a UNP with a centre-of-mass oscillation frequency that matches that of the desired density. We term this desired density the ‘target density’.
To measure the density of the UNP, we apply an RF field resonant with the electron centre-of-mass oscillation frequency when the UNP is at the target density. This RF field is applied for $1\, \mathrm {\mu }\mathrm {s}$![]() just after the triangle sequence. Through altering the 780 nm laser intensity during photoionization, the number of photoionized atoms is controlled and the density modified. The RF field amplitude is set to be large enough to drive up to 10 % of the electrons out of the UNP. When the electron/ion number matches the number associated with the resonant density conditions, electrons are maximally driven out of the UNP (Wilson et al. Reference Wilson, Chen and Roberts2013a). This occurs because the electron component centre-of-mass oscillation amplitude is at its largest when driven resonantly, producing the maximum value of internal electric fields that drive energetic electrons from the UNP, and therefore producing the maximum electron escape number. By measuring the electron escape as a function of total electron number, the electron number associated with the resonant response is found. See figure 5 for an example of the electron escape number right after the application of the RF field plotted as a function of the number of total electrons (and therefore total ions).
just after the triangle sequence. Through altering the 780 nm laser intensity during photoionization, the number of photoionized atoms is controlled and the density modified. The RF field amplitude is set to be large enough to drive up to 10 % of the electrons out of the UNP. When the electron/ion number matches the number associated with the resonant density conditions, electrons are maximally driven out of the UNP (Wilson et al. Reference Wilson, Chen and Roberts2013a). This occurs because the electron component centre-of-mass oscillation amplitude is at its largest when driven resonantly, producing the maximum value of internal electric fields that drive energetic electrons from the UNP, and therefore producing the maximum electron escape number. By measuring the electron escape as a function of total electron number, the electron number associated with the resonant response is found. See figure 5 for an example of the electron escape number right after the application of the RF field plotted as a function of the number of total electrons (and therefore total ions).

Figure 5. Resonant frequency density measurement. The electron escape number versus total electron number is plotted for conditions where a 16 MHz RF field is applied. Each black circle is an individual measurement. The fit function (blue line) is empirical based on the observed shape of the UNP response to resonant RF. The reason that it does not go to zero at higher electron number is that the electron oscillation amplitude goes to a finite value for UNPs with higher resonant frequencies than the driving field, similar to the behaviour of a driven harmonic oscillator. The value of the total number of electrons on the $x$![]() -axis that corresponds to the maximum of the fit function determines the target number for future measurements and corresponds to the electron number that matches our chosen density.
-axis that corresponds to the maximum of the fit function determines the target number for future measurements and corresponds to the electron number that matches our chosen density.
The total electron number associated with the peak electron escape response is identified as the ‘target number’, and subsequent data is collected with settings that produce a total electron number around the target number to produce UNPs with the desired density.
Numerical simulations are used to relate the RF resonant frequency to the UNP average electron density. The MC simulation described in § 2.2 is the simulation technique that was usually used, after confirming that the electron–ion collision rate did not have a significant effect on the resonance frequency for our UNP conditions. Within the simulation, an RF field was applied at the frequency and amplitude used in the experiment (see § 4.2 for the RF amplitude calibration), and the number of electrons and ions were varied while keeping the electron-to-ion ratio fixed to the value measured in the experimental data associated with this calibration. The electron escape number in response to the RF field was found as a function of the electron number, and the peak escape number was associated with the resonant condition.
Since the runtimes of the simulations were faster with smaller numbers, the resonant density was found for simulated UNPs smaller than the experimental numbers (i.e. the simulated UNPs had smaller spatial sizes). Because of this, simulations were conducted as a function of the total electron number to make sure that the simulation results converged to a high-number limit.
Figure 6 shows an example of simulation results used to determine the average UNP density along with a check on the convergence.

Figure 6. Example of MC simulation results used to determine the density associated with a resonant RF response. The simulated RF frequency was 16 MHz for this data. The main figure shows the electron escape rate for a UNP with initial electron number specified along the $x$![]() axis and spatial size $\sigma =0.416$
axis and spatial size $\sigma =0.416$![]() mm where the ion density is specified as $n_0 \exp (-({r^2}/{2 \sigma ^2}))$
mm where the ion density is specified as $n_0 \exp (-({r^2}/{2 \sigma ^2}))$![]() where $r$
where $r$![]() is the distance from the centre of the plasma and $n_0$
is the distance from the centre of the plasma and $n_0$![]() is the peak density. The electron-to-ion ratio was $0.75:1$
is the peak density. The electron-to-ion ratio was $0.75:1$![]() for this simulation. The inset shows the resonant frequency as a function of electron number to ensure that the number-dependent shift is sufficiently small at higher numbers.
for this simulation. The inset shows the resonant frequency as a function of electron number to ensure that the number-dependent shift is sufficiently small at higher numbers.
3.2 Reducing uncertainty associated with shot-to-shot electron number variation
Before presenting calibrations that rely on the PEF signal described above, a description of how PEF data is analysed is presented in this section. There is a significant variation in the shot-to-shot number of atoms photoionized. There are several contributions to this variation: variation in the number of atoms loaded into the AH magnetic trap due to noise in the MOT laser frequencies; shot-to-shot variations in the detuning of the 780 nm laser during photoionization; and variations in the MCP background due to electrical pick-up from changing magnetic field currents and the flashlamp for the pump laser that is used to create the 479 nm photoionization light. Electric pick-up is also responsible for the 780 nm laser detuning variation, too. This variation is not constant from day-to-day, but is typically in the range of 18 %–25 %.
For each MCP trace, however, we are able to determine the total number of electrons (and therefore ions). This information allows us to reduce the uncertainty in the PEF. While the PEF increases with increasing total ionized atom number (and therefore total ion number), this increase is not linear. Because of that, a simple division of the PEF by the ion number is insufficient to correct for the PEF shot-to-shot variation associated with the ion number variation. However, the change in PEF versus total ion number can be well-approximated by a second-order polynomial. For each data set taken under a particular set of experimental parameters, such a quadratic polynomial is fitted to the PEF versus total ion number. From this polynomial, the best fit PEF value at the ion number associated with the target density can be found for the experimental parameters. The uncertainty in this best-fit value can be determined as well. The PEF at the target density can then be compared across different experimental parameters such as different types of heating mechanisms or differed applied RF heating amplitudes. Figure 7 shows the variation of the number of electrons in the PEF signal with total electron number for typical conditions during a measurement and the quadratic curves fit to the data.

Figure 7. Fit functions used to compare PEF signals for different experimental conditions at a chosen total ion number. Four sets of PEF heating data are compared in this plot. The red points have no heating while the other three curves do. The blue data corresponds to a slow turn-off RF heating curve as described in § 4.2. The green and purple data correspond to fast turn-off heating data with the green having 2/3 the RF amplitude of the purple. Quadratic fit curves are shown, and best-fit values and uncertainties near the target number of 250 000 can be obtained. Linear interpolation can be used to accurately match the fast turn-off RF amplitude to the slow. The fractional uncertainty of the matching RF amplitude is 5.1 % for these data. Note that the total ion number is equal to the total electron number.
This method of data analysis only marginally improves the precision of the PEF determination as compared with a straight average. However, it avoids two sources of systematic error. Since the PEF increase is not linear with the increase in total ion number, a straight average introduces a distortion since the PEF nonlinearity versus ion number is not included in the straight average. Also, different sets can have different average ion numbers due to drifts, although the data is collected so that measurements with different conditions are interleaved such that drifts are not as significant (Yashchuk Reference Yashchuk2009). This number drift would also lead to a distortion if a straight average were used.
Now that the data analysis method used for analysing PEF signals has been presented, the discussion of the calibration techniques used to support our measurement technique is resumed.
3.3 Photoionization-energy-based calibration
A calibrated electron temperature increase is necessary in order to use our heating measurement technique. One way to calibrate such an electron temperature increase is through tuning the photoionizing 479 nm laser wavelength, and thus electron ionization energy, by a known amount. This relates the resulting change in PEF to a known electron temperature increase. For this calibration, we rely on the resettability of the MKS Instruments Cobra Stretch laser that we use to produce the 479 nm light, which is specified to have a precision ${<}2\,\mathrm {pm}$![]() . This corresponds to $0.1\,\mathrm {K}$
. This corresponds to $0.1\,\mathrm {K}$![]() of electron temperature reproducibility.
of electron temperature reproducibility.
In order for this electron temperature increase to be known, the UNP conditions need to be such that the change in electron temperature with photoionization laser wavelength is free of significant complicating factors. We choose an initial electron temperature that is high enough to have minimal Rydberg atom formation in the UNP (Killian et al. Reference Killian, Lim, Kulin, Dumke, Bergeson and Rolston2001; Fletcher, Zhang & Rolston Reference Fletcher, Zhang and Rolston2007; Bannasch & Pohl Reference Bannasch and Pohl2011). To confirm this was the case, we measured the Rydberg atom fraction present in the UNP. After all electrons had been extracted from the UNP by the final extraction field, we applied an RF field whose frequency was slow enough to be considered a DC field for the purposes of Rydberg selective field ionization. For all electron temperatures used for RF heating measurements, no Rydberg atoms were detected. At lower electron temperatures, a Rydberg signal is detected. Heating effects such as disorder-induced heating (Gericke & Murillo Reference Gericke and Murillo2003) and DC electric field heating (Jiang & Roberts Reference Jiang and Roberts2019) are present but essentially constant contributions at each photoionization energy in the range used.
It is straightforward to increase the photoionization laser wavelength from one setting to another with a photon energy $4.14 \times 10^{-23}$![]() J higher to raise the initial electron temperature by 2 K. The main complication is that increasing the initial electron temperature by 2 K also increases the fraction of electrons that escape from the plasma during the triangle ramp by 2 % for our most typical conditions. It is possible to counteract this initial increase in escape by reducing the amplitude of the triangle ramp.
J higher to raise the initial electron temperature by 2 K. The main complication is that increasing the initial electron temperature by 2 K also increases the fraction of electrons that escape from the plasma during the triangle ramp by 2 % for our most typical conditions. It is possible to counteract this initial increase in escape by reducing the amplitude of the triangle ramp.
To account for this modified initial escape effect, we collected data at the lower temperature $T_0$![]() for one triangle ramp amplitude, data at $T_0+2$
for one triangle ramp amplitude, data at $T_0+2$![]() K for the same triangle ramp amplitude and data at $T_0+2$
K for the same triangle ramp amplitude and data at $T_0+2$![]() K with a smaller triangle ramp amplitude. The determination of the initial temperature $T_0$
K with a smaller triangle ramp amplitude. The determination of the initial temperature $T_0$![]() will be discussed in § 3.5 below. By integrating the electron escape signal from the start to just before the PEF ramp (see figure 1) and knowing the total electron number and the fact that the total electron number equals the ion number, the net charge balance of the UNP just before the PEF ramp can be determined. Recall that the UNP confinement is deep enough that no electrons escape between the end of the first triangle ramp and the initiation of the PEF ramp. The net charge balance is the quantity that needs to be the same between two different heating conditions (that have the same total number) in order for matching PEF signals to indicate matching temperature increases. Figure 8(a) shows such electron escape data as a function of the total electron number for the three conditions described at the start of this paragraph. Linear interpolation is used to find the triangle ramp amplitude at $T_0 +2$
will be discussed in § 3.5 below. By integrating the electron escape signal from the start to just before the PEF ramp (see figure 1) and knowing the total electron number and the fact that the total electron number equals the ion number, the net charge balance of the UNP just before the PEF ramp can be determined. Recall that the UNP confinement is deep enough that no electrons escape between the end of the first triangle ramp and the initiation of the PEF ramp. The net charge balance is the quantity that needs to be the same between two different heating conditions (that have the same total number) in order for matching PEF signals to indicate matching temperature increases. Figure 8(a) shows such electron escape data as a function of the total electron number for the three conditions described at the start of this paragraph. Linear interpolation is used to find the triangle ramp amplitude at $T_0 +2$![]() K that matches the electron escape fraction at $T_0$
K that matches the electron escape fraction at $T_0$![]() .
.

Figure 8. Calibration of the PEF to a deliberate change in photoionization energy and kick-pulse calibration. Panel (a) shows the initial electron escape number from formation to the partial extraction ramp versus total electron number for three conditions: initial electron temperature $T_0$![]() with a triangle ramp amplitude of 600 mV (black and open circles); initial electron temperature $T_0 +2$
with a triangle ramp amplitude of 600 mV (black and open circles); initial electron temperature $T_0 +2$![]() K with a triangle ramp amplitude of 600 mV (green filled circles); and initial electron temperature $T_0$
K with a triangle ramp amplitude of 600 mV (green filled circles); and initial electron temperature $T_0$![]() with a triangle ramp amplitude of 550 mV (orange triangles). The ramp amplitude is expressed in experimental units. The solid lines on the plot are quadratic fits to the data while the vertical dotted line is the total electron number that corresponds to the target density. Linear interpolation indicates that a $T_0+2$
with a triangle ramp amplitude of 550 mV (orange triangles). The ramp amplitude is expressed in experimental units. The solid lines on the plot are quadratic fits to the data while the vertical dotted line is the total electron number that corresponds to the target density. Linear interpolation indicates that a $T_0+2$![]() K amplitude of $583.9 \pm 4.5$
K amplitude of $583.9 \pm 4.5$![]() mV matches the initial electron escape for $T_0$
mV matches the initial electron escape for $T_0$![]() . Panel (b) shows the PEF number versus kick amplitude (solid points) matched to the PEF number derived from the $T_0+2$
. Panel (b) shows the PEF number versus kick amplitude (solid points) matched to the PEF number derived from the $T_0+2$![]() K data (horizontal solid line, with the horizontal dotted lines indicating the uncertainty) at the adjusted triangle ramp amplitude determined from the data in panel (a). A quadratic fit is used to interpolate the data and standard error propagation determines the uncertainty. Statistical fluctuations occasionally cause the best fit quadratic function to dip negatively as shown in this plot. Those fluctuations are incorporated into the uncertainty analysis using standard error propagation. Constraining the fit to a positive slope produces less than 0.5 % shift in the matching kick amplitude.
K data (horizontal solid line, with the horizontal dotted lines indicating the uncertainty) at the adjusted triangle ramp amplitude determined from the data in panel (a). A quadratic fit is used to interpolate the data and standard error propagation determines the uncertainty. Statistical fluctuations occasionally cause the best fit quadratic function to dip negatively as shown in this plot. Those fluctuations are incorporated into the uncertainty analysis using standard error propagation. Constraining the fit to a positive slope produces less than 0.5 % shift in the matching kick amplitude.
3.4 Electric field short-pulse heating
In principle, the photoionization-calibrated PEF described in the previous subsection could be used as the calibrated PEF signal to compare with other heating methods such as RF heating. However, accounting for the variation in initial electron escape with photoionization energy requires more data than is desirable since data with multiple triangle ramp amplitudes need to be collected and the interpolation adds uncertainty to the measurements due to statistical noise. To overcome this difficulty, we related another heating mechanism to the photoionization-calibrated PEF that does not have the same limitations with respect to initial electron escape.
The UNP electrons can be heated by applying an electric field pulse with a duration which is short compared with the electron centre-of-mass oscillation period (Chen et al. Reference Chen, Witte and Roberts2017). This pulse is applied 500 ns after the completion of the triangle sequence. It has a 16 ns full-width half-maximum duration and a controllable amplitude, and it delivers an impulse-like acceleration to the electrons relative to the ions. We call this a ‘kick’ pulse. The electrons respond to this kick pulse by oscillating with respect to the ions. Electron–ion collisions damp this oscillation, resulting in the conversion of the oscillation energy to electron thermal energy. For our UNP conditions, the results of Glinsky et al. (Reference Glinsky, O’Neil, Rosenbluth, Tsuruta and Ichimaru1992) indicate that the $4\,\mathrm {\mu }\mathrm {s}$![]() delay between the end of the triangle ramp and the start of the PEF ramp is a full order of magnitude greater than the equipartition time for our UNP conditions.
delay between the end of the triangle ramp and the start of the PEF ramp is a full order of magnitude greater than the equipartition time for our UNP conditions.
The advantage of this kick pulse is that the amount of heating imparted to the electrons is set only by the pulse duration, pulse amplitude and centre-of-mass oscillation frequency of the electrons. We keep the pulse duration fixed and analyse our data at the ‘target number’ to keep the centre-of-mass oscillation fixed for our measurements. Since the testing phase when either a kick pulse or RF field is applied comes after the initial triangle ramp phase, the UNP charge imbalance will be the same for either heating mechanism so long as the initial electron temperature and triangle ramp amplitude are also the same.
To calibrate the amount of heating induced by the kick pulse, we collect PEF data as a function of kick amplitude. We then compared and matched that data with the photoionization-calibrated PEF, accounting for the difference in the initial electron escape as described above via data shown in figure 8(a). Figure 8(b) shows an example set of data for this sort of measurement. For that data, 400 shots were collected and a 7 % precision was obtained for determining the kick amplitude that matched the 2 K heating.
3.5 Initial electron temperature
The calibration of PEF change due to heating and the calibration of the kick heating require knowing a change in temperature, not an absolute value of the electron temperature. To compare measurements with predictions, the value of the initial electron temperature $T_0$![]() is necessary, however. Determination of this initial temperature requires auxiliary measurements, but ultimately relies on simulations to account for heating contributions.
is necessary, however. Determination of this initial temperature requires auxiliary measurements, but ultimately relies on simulations to account for heating contributions.
The calibration of the 479 nm photoionization wavelength with respect to the $^{85}$![]() Rb ionization threshold is one quantity that needs to be measured to determine the electrons’ initial kinetic energy. Additionally, stray electric fields in the UNP region result in electron heating during formation as well (Jiang & Roberts Reference Jiang and Roberts2019). To characterize both of these, we perform auxiliary measurements of Rydberg atoms at low-density (less than $10^{12}\,\mathrm {m}^{-3}$
Rb ionization threshold is one quantity that needs to be measured to determine the electrons’ initial kinetic energy. Additionally, stray electric fields in the UNP region result in electron heating during formation as well (Jiang & Roberts Reference Jiang and Roberts2019). To characterize both of these, we perform auxiliary measurements of Rydberg atoms at low-density (less than $10^{12}\,\mathrm {m}^{-3}$![]() ) conditions created through below-ionization-threshold excitation with the 479 nm laser. In other words, we create Rydberg atoms rather than a UNP. By applying an electric field to the Rydberg atoms and scanning the 479 nm laser wavelength across repeated measurements, we can find the ionization threshold at that electric field (Cooke & Gallagher Reference Cooke and Gallagher1978). The MD simulations indicate that for our conditions, the electric field ionization threshold is reached when 50 % of the Rydberg atoms are ionized. To measure the ionization fraction at a chosen 479 nm wavelength, a simplified DC field sequence is used that consists of the chosen DC field applied during ionization to measure the number of Rydberg atoms ionized by that field followed by a rapid (200 ns) increase to $30\,{\rm V}\,{\rm m}^{-1}$
) conditions created through below-ionization-threshold excitation with the 479 nm laser. In other words, we create Rydberg atoms rather than a UNP. By applying an electric field to the Rydberg atoms and scanning the 479 nm laser wavelength across repeated measurements, we can find the ionization threshold at that electric field (Cooke & Gallagher Reference Cooke and Gallagher1978). The MD simulations indicate that for our conditions, the electric field ionization threshold is reached when 50 % of the Rydberg atoms are ionized. To measure the ionization fraction at a chosen 479 nm wavelength, a simplified DC field sequence is used that consists of the chosen DC field applied during ionization to measure the number of Rydberg atoms ionized by that field followed by a rapid (200 ns) increase to $30\,{\rm V}\,{\rm m}^{-1}$![]() after $2\, \mathrm {\mu }\mathrm {s}$
after $2\, \mathrm {\mu }\mathrm {s}$![]() to ionize all the Rydberg atoms to count the total number. Figure 9(a) shows data obtained from such a measurement. This measurement is then repeated for different applied electric field strengths during photoionization.
to ionize all the Rydberg atoms to count the total number. Figure 9(a) shows data obtained from such a measurement. This measurement is then repeated for different applied electric field strengths during photoionization.

Figure 9. Calibration data used to calibrate the 479 nm photoionization laser wavelength and stray electric fields in the UNP region. Panel (a) shows the ionization fraction of a low-density gas of Rydberg atoms when a $6.8\,{\rm V}\,{\rm m}^{-1}$![]() electric field is applied as a function of the 479 nm wavelength input into the laser controller. The red line is an interpolating function that is used to determine the wavelength at which 50 % of the Rydberg atoms are ionized. Panel (b) shows the ionization wavelength input into the laser controller as a function of applied electric field. Note that this is not the true value of the laser wavelength. The line represents a fit to the data.
electric field is applied as a function of the 479 nm wavelength input into the laser controller. The red line is an interpolating function that is used to determine the wavelength at which 50 % of the Rydberg atoms are ionized. Panel (b) shows the ionization wavelength input into the laser controller as a function of applied electric field. Note that this is not the true value of the laser wavelength. The line represents a fit to the data.
From this data we can determine both the precise 479 nm wavelength associated with the ionization threshold and the size of stray electric fields at the location of the plasma. The data in figure 9 indicate a $18.2\pm 0.7$![]() pm shift in the 479 nm laser wavelength to the blue from the controller value and a stray field of $4.2\pm 0.3\,{\rm V}\,{\rm m}^{-1}$
pm shift in the 479 nm laser wavelength to the blue from the controller value and a stray field of $4.2\pm 0.3\,{\rm V}\,{\rm m}^{-1}$![]() .
.
With that information, we model the UNP formation process for our parameters in an MC numerical simulation to account for heating effects from the stray fields and any contribution from the first triangle sequence to determine the electron temperature. This captures disorder-induced heating effects (Gericke & Murillo Reference Gericke and Murillo2003), but not continuum lowering effects (Stewart & Pyatt Reference Stewart and Pyatt1966). However, an estimate of the temperature effect of the latter ($0.2\,\mathrm {K}$![]() ) based on Stewart & Pyatt (Reference Stewart and Pyatt1966) is not only of the order of the temperature uncertainty but MD simulations show that it is not more than half that amount for our plasma conditions and consistent with zero effect at that level of precision. We estimate the systematic uncertainty in the determination of the electron temperature to be $0.3\,\mathrm {K}$
) based on Stewart & Pyatt (Reference Stewart and Pyatt1966) is not only of the order of the temperature uncertainty but MD simulations show that it is not more than half that amount for our plasma conditions and consistent with zero effect at that level of precision. We estimate the systematic uncertainty in the determination of the electron temperature to be $0.3\,\mathrm {K}$![]() using these techniques based on the uncertainties in the wavelength calibration and stray electric field, with the primary contribution coming from the uncertainty in the stray electric field. For the data presented in this article, the electron temperature after the triangle ramp is estimated to be $5.07 \pm 0.30\, \mathrm {K}$
using these techniques based on the uncertainties in the wavelength calibration and stray electric field, with the primary contribution coming from the uncertainty in the stray electric field. For the data presented in this article, the electron temperature after the triangle ramp is estimated to be $5.07 \pm 0.30\, \mathrm {K}$![]() .
.
Given our UNP densities of $1.1 \times 10^{13}\,\mathrm {m}^{-3}$![]() , the strong coupling parameter $\varGamma = 0.12$
, the strong coupling parameter $\varGamma = 0.12$![]() at this electron temperature (Ichimaru Reference Ichimaru1982). While our plasma electron temperatures are very cold, the plasma is not strongly coupled. The UNP properties such as the number of electrons that escape due to the initial triangle ramp are consistent with simulation results at these electron temperatures. Further, MD simulations for electrons with the initial ionization energy associated with the calibrated 479 nm wavelength do not show any sources of unusual heating. The UNPs under similar conditions have shown agreement with simulations for temperature-dependent properties such as oscillation damping for even colder temperatures (Chen et al. Reference Chen, Witte and Roberts2017).
at this electron temperature (Ichimaru Reference Ichimaru1982). While our plasma electron temperatures are very cold, the plasma is not strongly coupled. The UNP properties such as the number of electrons that escape due to the initial triangle ramp are consistent with simulation results at these electron temperatures. Further, MD simulations for electrons with the initial ionization energy associated with the calibrated 479 nm wavelength do not show any sources of unusual heating. The UNPs under similar conditions have shown agreement with simulations for temperature-dependent properties such as oscillation damping for even colder temperatures (Chen et al. Reference Chen, Witte and Roberts2017).
4 The RF heating rate measurements in UNPs
4.1 Measurement of high-frequency RF heating rates
The interest in measuring the RF heating rate is that the heating rate is directly related to the absorptive part of the AC conductivity of the plasma (Oberman & Shure Reference Oberman and Shure1963; Chen Reference Chen1974; Matsuda Reference Matsuda1981). This AC conductivity is in turn related to the electron–ion collision rate in the plasma (Nersisyan, Zwicknagle & Deutsch Reference Nersisyan, Zwicknagle and Deutsch2019). The RF heating can therefore be used to investigate the AC conductivity and electron–ion collision rate as a function of plasma conditions. We seek to measure the AC conductivity and electron–ion collision rate as a function of electron magnetization (Baalrud & Daligault Reference Baalrud and Daligault2017). These measurements are still under analysis and will appear in a future publication. This article relays the experimental technique that we developed to make these measurements.
To date, our experiments are conducted with the directions of both the applied RF electric field and the magnetic field along the same axis. A 1.07 mT applied magnetic field is generated along the $z$![]() -axis by a coil wrapped around the vacuum chamber (see figure 2 and its associated caption). The RF electric field applied to the plasma is generated by an arbitrary function generator (AFG) connected to the copper disk illustrated in figures 2 and 3. Since the directions of the magnetic and electric fields are coaxial, the longitudinal (as opposed to transverse) AC conductivity of the plasma is being measured.
-axis by a coil wrapped around the vacuum chamber (see figure 2 and its associated caption). The RF electric field applied to the plasma is generated by an arbitrary function generator (AFG) connected to the copper disk illustrated in figures 2 and 3. Since the directions of the magnetic and electric fields are coaxial, the longitudinal (as opposed to transverse) AC conductivity of the plasma is being measured.
We conducted our measurements using an RF frequency that was higher than both the centre-of-mass oscillation frequency and the local electron plasma frequency at the densest part of the UNP. We chose this high-frequency limit to remove an experimental complication that would exist at lower frequencies. In the absence of any electron–ion collisions, there is no heating in the high-frequency limit for our conditions. This was confirmed with an MC simulation of our plasma. All of the electrons move together in the same centre-of-mass frame, so electron–electron collisions cannot transfer RF-induced motion to electron heating. Since electron–electron collisions do not contribute to heating, any RF heating is due to electron–ion collisions. In the low-frequency limit, this last statement is not true because the electron spatial distribution has time to change during the RF-induced oscillation. The change in relative motion of the electrons means that electron–electron collisions can transform RF-induced motion to electron thermal energy. Changes in the shape of the electron distribution during an RF oscillation period would produce a heating source separate from the heating associated with the absorptive part of the AC conductivity.
The goal of the RF heating measurements is to find the RF amplitude that produces the same PEF as kick-induced heating for a given set of UNP conditions. The RF heating data are taken at several RF amplitudes by changing the amplitude of the waveform generated by the AFG. The RF heating PEF measured at each AFG amplitude is compared with the calibrated kick-induced heating PEF to find the AFG amplitude at which the RF heating matched the kick-induced heating. These measurements determine the AFG amplitude that produces a 2 K change in electron temperature at our plasma conditions. The calibration factor that gives the amplitude of the RF field at the plasma for a given AFG amplitude is determined using the methods described in § 4.2.
Figure 10 shows an example of how this matching is performed. The PEF versus RF amplitude is fitted with a quadratic function, and the amplitude that matches the kick-induced PEF is computed along with the associated uncertainty using standard error propagation. For RF amplitudes small enough that nonlinear heating effects are negligible, the RF heating will be proportional to the square of the RF electric field amplitude. The heating scales as the square of the RF amplitude in the absence of nonlinear effects because the RF-induced electron acceleration and displacement are both proportional to the electric field amplitude, so the work done on the electrons by the RF electric field scales as the square of the electric field amplitude. For our experimental conditions, nonlinear effects are expected to be less than the measurement uncertainty (Guthrie & Roberts Reference Guthrie and Roberts2021).

Figure 10. Matching the amount of heating between two different conditions. The data points show PEF values measured at three different applied RF amplitudes and the dotted curve shows a quadratic fit to that data. The RF heating is matched to the PEF of the calibrating condition, which is represented by the solid orange line, using the quadratic fit. Uncertainty in the fit value is obtained using standard error propagation. The $1\sigma$![]() uncertainty range of the calibrating condition above and below the central PEF value is shown with dotted orange lines. The matching RF amplitude for this data set is $35.2 \pm 2.2\,\mathrm {V}\,\mathrm {m}^{-1}$
uncertainty range of the calibrating condition above and below the central PEF value is shown with dotted orange lines. The matching RF amplitude for this data set is $35.2 \pm 2.2\,\mathrm {V}\,\mathrm {m}^{-1}$![]() .
.
We have observed that heating rates derived for similar, but not exactly the same, experimental conditions with significantly different heating amounts have still produced the same heating rates within measurement uncertainties (typically 20 %–30 %), indicating a lack of any strong nonlinear effects. As one example, the heating amount was different by 30 % for two experimental conditions that were otherwise similar. The heating rate ratio of the higher heating amount data to the lower was $1.08\pm 0.19$![]() after correcting for a 23 % difference in density. This data is displayed in table 2. It should be noted that the comparison between these data sets is not a direct one. The difficulty with directly comparing data with different heating amounts is that the average temperature during the heating is not the same if the starting temperature is the same. Direct comparisons require significant amounts of data and iteration.
after correcting for a 23 % difference in density. This data is displayed in table 2. It should be noted that the comparison between these data sets is not a direct one. The difficulty with directly comparing data with different heating amounts is that the average temperature during the heating is not the same if the starting temperature is the same. Direct comparisons require significant amounts of data and iteration.
Table 2. Data relevant to the nonlinear scaling check described in the main text. All data shown were collected at a magnetic field of 1.07 mT and initial electron temperature of $5.07\,\mathrm {K}$![]() .
.

Typical data sets consisted of approximately 40 shots per AFG amplitude for three AFG amplitudes, another 40 shots for the kick-induced heating, plus another 40 shots with no heating pulses applied. It takes approximately 6–10 hr to collect such a set of data. The precision of the determination of the AFG amplitude that matches the kick-induced heating was typically several per cent from such a set of data. The overall uncertainty of this determination is dominated by the statistical uncertainty in the measured PEFs. Since the heating scales as the RF amplitude squared, the uncertainty of the measured heating rate is at least twice the uncertainty of the RF amplitude. So, a single such set of RF heating data produces a measured heating rate with typically 10 %–15 % precision.
4.2 Calibration of the RF electric field amplitude
The determination of the absolute RF heating rate based on the method described in § 4.1 relies on the calibration of the RF field amplitude generated by the AFG. Direct calculation of the value of the RF amplitude at the location of the UNP is impractical given the construction of the electrodes and housings in the vacuum chamber. Instead, we developed a technique to measure the RF field amplitude by applying different RF waveforms that heat the UNP in different ways.
As long as the applied RF frequency is sufficiently higher than the electron centre-of- mass oscillation frequency in the UNP, the electron positions will oscillate approximately $180^{\circ }$![]() out of phase with the applied RF field in the same way that a harmonic oscillator does when driven by a frequency higher than its resonant frequency. If the applied field is turned off suddenly at a zero crossing, the electrons will then oscillate with an amplitude determined by their maximal centre-of-mass velocity induced by the applied RF. This centre-of-mass velocity is proportional to the RF amplitude. Just like when the UNP is subjected to a kick pulse, the electron oscillation from this RF field sudden turn-off damps and turns into electron heating.
out of phase with the applied RF field in the same way that a harmonic oscillator does when driven by a frequency higher than its resonant frequency. If the applied field is turned off suddenly at a zero crossing, the electrons will then oscillate with an amplitude determined by their maximal centre-of-mass velocity induced by the applied RF. This centre-of-mass velocity is proportional to the RF amplitude. Just like when the UNP is subjected to a kick pulse, the electron oscillation from this RF field sudden turn-off damps and turns into electron heating.
We compared two different RF heating sequences using our PEF matching technique. The first was one where the RF was turned on slowly, turned off slowly and applied for a total of $1.2\,\mathrm {\mu }\mathrm {s}$![]() . In the second condition, the RF was turned on slowly but turned off suddenly after $400\,\mathrm {ns}$
. In the second condition, the RF was turned on slowly but turned off suddenly after $400\,\mathrm {ns}$![]() . The turn-off was programmed to happen at a zero crossing of the RF field. See figure 11 for a plot of the ideal RF waveforms of this measurement. Due to finite response times and the inductance and capacitance of elements in the RF circuit, additional corrections were included to determine the RF amplitude calibration, but the general idea remains the same. These corrections will be addressed at the end of this section.
. The turn-off was programmed to happen at a zero crossing of the RF field. See figure 11 for a plot of the ideal RF waveforms of this measurement. Due to finite response times and the inductance and capacitance of elements in the RF circuit, additional corrections were included to determine the RF amplitude calibration, but the general idea remains the same. These corrections will be addressed at the end of this section.

Figure 11. Ideal waveforms for the RF amplitude calibration. The grey waveform is for the slow turn-off and the red represents the fast. Turning off the RF field at a zero crossing means that at that time the electron centre-of-mass oscillation velocity is near its maximum.
Consider a model of the UNP electron response when driven by an oscillating electric field $\boldsymbol {E}(t) = E_0\sin {(\omega _{{\rm RF}}t + \phi _0)}\hat {z}$![]() , where $\omega _{{\rm RF}}$
, where $\omega _{{\rm RF}}$![]() is the RF frequency and $\phi _0$
is the RF frequency and $\phi _0$![]() is an arbitrary phase we may set to zero. The motion of the electrons in the high-RF-frequency limit can be approximately described by the solution to the damped–driven harmonic oscillator equation
is an arbitrary phase we may set to zero. The motion of the electrons in the high-RF-frequency limit can be approximately described by the solution to the damped–driven harmonic oscillator equation
where $\omega _{{\rm CM}}$![]() is the centre-of-mass oscillation frequency with $\omega _{{\rm CM}} \ll \omega _{{\rm RF}}$
is the centre-of-mass oscillation frequency with $\omega _{{\rm CM}} \ll \omega _{{\rm RF}}$![]() ; $b$
; $b$![]() is a drag coefficient that depends on plasma parameters such as temperature, density and applied magnetic field strength; and $z_0$
is a drag coefficient that depends on plasma parameters such as temperature, density and applied magnetic field strength; and $z_0$![]() is the location of the centre of the plasma that we may set as the origin. The solution for the electron position under these conditions is sinusoidal with amplitude and phase
is the location of the centre of the plasma that we may set as the origin. The solution for the electron position under these conditions is sinusoidal with amplitude and phase

The work done on the electron by the RF field can be calculated from the electron trajectory and the force applied to the electron by the RF field. This work corresponds to the change in electron energy $\Delta E$![]() that eventually turns into RF induced heating. The amount of heating predicted by this model ultimately depends on $E(t)$
that eventually turns into RF induced heating. The amount of heating predicted by this model ultimately depends on $E(t)$![]() , $\omega _{{\rm CM}}$
, $\omega _{{\rm CM}}$![]() and $b$
and $b$![]() . So, if $\Delta E$
. So, if $\Delta E$![]() , $\omega _{{\rm CM}}$
, $\omega _{{\rm CM}}$![]() and the shape of the RF waveform $\boldsymbol {E}(t)/E_0$
and the shape of the RF waveform $\boldsymbol {E}(t)/E_0$![]() are known, then the remaining two parameters $E_0$
are known, then the remaining two parameters $E_0$![]() and $b$
and $b$![]() may be determined by making two separate RF heating measurements. This is true regardless when the turn-off occurs in the RF field oscillation cycle as long as the RF waveform shape is known. This is the general idea for determining the RF amplitude calibration factor using the two different RF waveforms illustrated in figure 11.
may be determined by making two separate RF heating measurements. This is true regardless when the turn-off occurs in the RF field oscillation cycle as long as the RF waveform shape is known. This is the general idea for determining the RF amplitude calibration factor using the two different RF waveforms illustrated in figure 11.
The RF heating measurements were performed by applying these two RF waveforms to UNPs with the same initial temperature, density and applied magnetic field. The amplitudes programmed into the AFG that generated the RF fields were varied to find the PEF that matches the kick-induced PEF calibrated to a 2 K temperature change. Interpolation was used to determine the AFG amplitudes for each waveform that generates 2 K of heating. These AFG amplitudes, modified by a calibration factor to convert the experimental units into an electric field, were fed into the damped–driven harmonic oscillator model. The calibration factor and drag coefficient $b$![]() were adjusted such that the model produced 2 K of heating for both RF waveforms.
were adjusted such that the model produced 2 K of heating for both RF waveforms.
While we used this technique to measure the RF field amplitude in our system, there are complications compared with the ideal case that had to be taken into account. It is not possible to turn off the applied electric field instantaneously. There is some ringing of the output voltage and current from the AFG. Figure 12 shows the actual turn-off of the RF and the associated ringing. By measuring the electrical response of our apparatus to sudden RF field turn-offs, we were able to match the response to a model resistor–inductor–capacitor (RLC) circuit. The circuit model was constructed to account for the capacitance of the copper disk in the vacuum chamber to which the RF was applied, the resistance and inductance in the system, and the capacitance and resistance of a coaxial probe cable connected to an oscilloscope. The circuit diagram for the electrical response model is illustrated in figure 13. Once we had characterized the effective electrical response of the apparatus, we input the corrected fast turn-off and slow turn-off waveforms into the damped–driven electron oscillation model and determined the plasma heating that would result. The corrected fast turn-off waveform produced by the RLC model is plotted alongside an example AFG trace measured by the probe cable in figure 12.

Figure 12. Modelling the fast turn-off. The blue (noisier) trace shows the voltage measured via a cable to an oscilloscope as described in the main text. The yellow is the output of the RLC-based model with parameters set to match the turn-off. Distortions due to reflections are visible on the right-hand side of the blue trace. These are not part of the model, so it does not include these features.

Figure 13. The circuit diagram for the electrical response model. The model was constructed to account for the resistance, capacitance and inductance for the vacuum chamber electrode to which the RF was applied and the resistance and capacitance of a coaxial probe cable connected to an oscilloscope. A parallel $50 \,\Omega$![]() terminator to ground at the output of the AFG is also included.
terminator to ground at the output of the AFG is also included.
The capacitance of the copper disk was measured by applying a 1 MHz oscillation and measuring the current that was drawn. The inductance and resistor in series with that capacitor contributed negligibly to the measured capacitance. The inductance was determined by the frequency of the ringing after the sudden turn-off. The effective capacitance of the probe cable was determined by the damping of that ringing. A parallel $50 \,\Omega$![]() terminator to ground at the output of the AFG was also present.
terminator to ground at the output of the AFG was also present.
The precision of the RF amplitude calibration is poorer than initially expected. There are estimated uncertainties of 8 % associated with modelling the non-ideal electrical response. More significantly, there are numerical factors such that a 5 % precision in the PEF associated with each of the slow and fast turn-off resulted in 17 % uncertainty in the calibration of the RF field amplitude. Given that heating is proportional to the square of the amplitude, the accuracy of obtained heating rates have close to a 40 % uncertainty when all sources of uncertainty are included. Possible improvements to this uncertainty are discussed below.
5 Determination of RF heating rate for a single set of experimental conditions
As a first full measurement that demonstrates the technique, data were collected for a UNP with density of $1.13\pm 0.01 \times 10^{13}\, \mathrm {m}^{-3}$![]() and initial temperature of $T_e = 5.07 \pm 0.30$
and initial temperature of $T_e = 5.07 \pm 0.30$![]() K. These data were collected for a plasma where the initial triangle ramp phase removed 23 % of the electrons. A magnetic field of $B=1.07$
K. These data were collected for a plasma where the initial triangle ramp phase removed 23 % of the electrons. A magnetic field of $B=1.07$![]() mT was applied. A kick that corresponded to $2.0 \pm 0.44\, \mathrm {K}$
mT was applied. A kick that corresponded to $2.0 \pm 0.44\, \mathrm {K}$![]() of temperature rise was used to find the calibrated PEF. The RF amplitude of a 60 MHz applied RF field was varied as described above to find the matching RF amplitude for this amount of heating. The RF field was turned on and off with a $32\,\mathrm {ns}$
of temperature rise was used to find the calibrated PEF. The RF amplitude of a 60 MHz applied RF field was varied as described above to find the matching RF amplitude for this amount of heating. The RF field was turned on and off with a $32\,\mathrm {ns}$![]() exponential time constant and applied for a total of $1.2\,\mathrm {\mu }\mathrm {s}$
exponential time constant and applied for a total of $1.2\,\mathrm {\mu }\mathrm {s}$![]() .
.
For these conditions the absorptive part of the longitudinal AC conductivity was measured to be
where the first uncertainty corresponds to the statistical uncertainty while the second reflects the systematic uncertainty. This can be compared with the predicted value (Guthrie & Roberts Reference Guthrie and Roberts2021) of $1.31 \times 10^{-5}\,\Omega ^{-1}\,\mathrm {m}^{-1}$![]() , which is in agreement well within the uncertainty of the measurement.
, which is in agreement well within the uncertainty of the measurement.
6 Improving performance
While the precision that can be obtained with this heating measurement technique is respectable at 10 %–15 % of the measured heating rate, data collection times can extend to 8 hr or longer to achieve this precision. Initially, data collection rates were even longer than this rate by a factor of approximately four. The sources of signal-to-noise limitations and possibilities for improvement are presented in this section.
The signal-to-noise is mainly dependent on three factors. The first is the reproducibility of the AH magnetic trap loading from the MOT. Variations in atom number at this stage translate to variations in the number of photoionized atoms and the spatial size of the atoms prior to photoionization (Chen, Witte & Roberts Reference Chen, Witte and Roberts2016). The second is the variation in 780 nm laser frequency during photoionization. We tune this laser to resonance, so random fluctuations decrease the number of ionized atoms. Finally, there is electromagnetic pick-up on the MCP signal associated with the flashlamp of the Nd-YAG laser that pumps our 479 nm tuneable dye laser and the multiple changing currents in magnetic-field-producing coils. This pick-up forms a background signal that varies from shot-to-shot and adds noise to our measurements, primarily through noise pick-up on the MCP signal itself but also by substantially increasing the random fluctuations of the 780 nm laser frequency.
We have found that better alignment of the MOT to produce the highest fraction of atoms trapped by the AH coils improves the reproducibility of the loading, and that gave us the signal-to-noise gain reported above. To further improve the stability, the diode laser used to produce the 780 nm light could be fibre-coupled from a location that better isolates it from electromagnetic noise. The MCP signal when no electrons are striking it (e.g. prior to photoionization) is analysed to apply a background subtraction that improves the signal-to-noise. More sophisticated subtraction techniques are possible by acquiring a large set of UNP-free background signals and systematically optimizing the background subtraction function. Collecting this data also provides an opportunity to observe changes in the background signal with time as well as possibly what effects are contributing most to the background noise.
The nearly 40 % uncertainty in the calibration of the absolute (as opposed to relative) value of the RF heating rate can also be improved. Additional data can be used to reduce this uncertainty, but the return on each additional data set diminishes due to the $\sqrt {N}$![]() precision obtained for $N$
precision obtained for $N$![]() measurements. A better option would be to use Rydberg atoms to sense the electric field amplitude at the location of the UNP (Holloway et al. Reference Holloway, Simons, Gordon, Dienstfrey, Anderson and Raithel2017; Ma et al. Reference Ma, Viray, Anderson and Raithel2022). A method of doing so adapted to our apparatus is in the process of being implemented. This will also remove the dependence of the calibration on the modelling of the non-ideal electrical response of the system as well.
measurements. A better option would be to use Rydberg atoms to sense the electric field amplitude at the location of the UNP (Holloway et al. Reference Holloway, Simons, Gordon, Dienstfrey, Anderson and Raithel2017; Ma et al. Reference Ma, Viray, Anderson and Raithel2022). A method of doing so adapted to our apparatus is in the process of being implemented. This will also remove the dependence of the calibration on the modelling of the non-ideal electrical response of the system as well.
7 Conclusion
We have described a technique for measuring electron heating in a UNP by an external field. While the focus of the reported work is on the heating rate from high-frequency RF fields, it is not restricted to that heating source. This technique finds parameters for which the heating from two different mechanisms is the same. By using a calibrated source as one of these mechanisms, an experimental measurement of the heating from another mechanism can be measured for comparison with theoretical predictions or other purposes. We used this technique to measure the AC conductivity of a UNP in the high-frequency regime. The reported measurement is an initial one of a series intended to measure the AC conductivity of a UNP as a function of electron magnetization. A statistical precision of approximately 13 % was obtained with several hours of data collection. Future improvements are expected to improve the signal-to-noise ratio of the measurement. The systematic uncertainty of close to 40 % is currently much greater than the precision of individual measurements owing to difficulties in calibrating the applied RF field amplitude. Relative measurements can be obtained with uncertainties at the statistical level of precision. This technique opens up study of RF heating in UNPs as a function of electron magnetization, electron temperature, electron density, strong coupling and RF amplitude.
Acknowledgements
Editor F. Califano thanks the referees for their advice in evaluating this article.
Funding
This work was supported by the Air Force Office of Scientific Research (grant numbers FA9550-17-1-0148,FA9550-21-1-0340).
Declaration of interests
The authors report no conflict of interest.
Data availability
The data that support the findings of this study are available upon reasonable request from the authors.