Article contents
Azimuthal magnetorotational instability with super-rotation
Published online by Cambridge University Press: 25 January 2018
Abstract
It is demonstrated that the azimuthal magnetorotational instability (AMRI) also works with radially increasing rotation rates contrary to the standard magnetorotational instability for axial fields which requires negative shear. The stability against non-axisymmetric perturbations of a conducting Taylor–Couette flow with positive shear under the influence of a toroidal magnetic field is considered if the background field between the cylinders is current free. For small magnetic Prandtl number 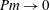 $Pm\rightarrow 0$ the curves of neutral stability converge in the (Hartmann number,Reynolds number) plane approximating the stability curve obtained in the inductionless limit
$Pm\rightarrow 0$ the curves of neutral stability converge in the (Hartmann number,Reynolds number) plane approximating the stability curve obtained in the inductionless limit 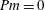 $Pm=0$. The numerical solutions for
$Pm=0$. The numerical solutions for 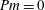 $Pm=0$ indicate the existence of a lower limit of the shear rate. For large
$Pm=0$ indicate the existence of a lower limit of the shear rate. For large  $Pm$ the curves scale with the magnetic Reynolds number of the outer cylinder but the flow is always stable for magnetic Prandtl number unity as is typical for double-diffusive instabilities. We are particularly interested to know the minimum Hartmann number for neutral stability. For models with resting or almost resting inner cylinder and with perfectly conducting cylinder material the minimum Hartmann number occurs for a radius ratio of
$Pm$ the curves scale with the magnetic Reynolds number of the outer cylinder but the flow is always stable for magnetic Prandtl number unity as is typical for double-diffusive instabilities. We are particularly interested to know the minimum Hartmann number for neutral stability. For models with resting or almost resting inner cylinder and with perfectly conducting cylinder material the minimum Hartmann number occurs for a radius ratio of 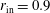 $r_{\text{in}}=0.9$. The corresponding critical Reynolds numbers are smaller than
$r_{\text{in}}=0.9$. The corresponding critical Reynolds numbers are smaller than 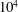 $10^{4}$.
$10^{4}$.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2018
References
- 6
- Cited by


