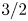1 Introduction
One of the major challenges facing magnetically confined fusion plasmas is the degradation of energy confinement due to transport. This transport arises because the density and temperature vary across the plasma volume, giving rise to neoclassical transport as well as free energy which drives instabilities, turbulence and transport. The dependence on the geometry of the magnetic field is well understood in the case of neoclassical transport, and stellarators can be designed in such a way as to minimize these losses (Wolf et al. Reference Wolf, Ali, Alonso, Baldzuhn, Beidler, Beurskens, Biedermann, Bosch, Bozhenkov and Brakel2017; Dinklage et al. Reference Dinklage, Beidler, Helander, Fuchert, Maaßberg, Rahbarnia, Pedersen, Turkin, Wolf and Alonso2018; Klinger et al. Reference Klinger2019; Beidler et al. Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Borchardt, Bozhenkov, Brunner and Damm2021).
The main transport channel is then turbulent transport, which typically exceeds the neoclassical channel, see e.g. Bozhenkov et al. (Reference Bozhenkov, Kazakov, Ford, Beurskens, Alcusón, Alonso, Baldzuhn, Brandt, Brunner and Damm2020) and Beidler et al. (Reference Beidler, Smith, Alonso, Andreeva, Baldzuhn, Beurskens, Borchardt, Bozhenkov, Brunner and Damm2021). Accordingly, insights into the interplay between turbulence and geometry are desired so that one can understand, and perhaps minimize, the turbulent losses. However, due to the complex nonlinear nature of the problem, it has proved difficult to quantify the dependence of turbulence on geometry, although significant strides have been made in recent years (Barnes, Parra & Schekochihin Reference Barnes, Parra and Schekochihin2011; Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander, Proll & Plunk Reference Helander, Proll and Plunk2013; Plunk et al. Reference Plunk, Helander, Xanthopoulos and Connor2014; Pueschel et al. Reference Pueschel, Faber, Citrin, Hegna, Terry and Hatch2016; Citrin et al. Reference Citrin, Bourdelle, Casson, Angioni, Bonanomi, Camenen, Garbet, Garzotti, Görler and Gürcan2017; Proll et al. Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). These methods, although not all of them, typically employ (quasi-)linear theory to estimate the turbulence properties for any given configuration. Such methods do not always capture important nonlinear effects and suffer, in particular, from uncertainties concerning the turbulent saturation amplitude. The most reliable option to assess nonlinear turbulent transport is to carry out nonlinear gyrokinetic simulations (Beer, Cowley & Hammett Reference Beer, Cowley and Hammett1995; Garbet et al. Reference Garbet, Idomura, Villard and Watanabe2010), but it is currently computationally expensive to do so, although significant improvements have been made (Mandell et al. Reference Mandell, Dorland, Abel, Gaur, Kim, Martin and Qian2022).
In a recent publication (Mackenbach, Proll & Helander Reference Mackenbach, Proll and Helander2022), it was shown that the so-called available energy (Æ) can provide a quantitative estimate of the turbulence driven by the trapped-electron mode (Kadomtsev & Pogutse Reference Kadomtsev and Pogutse1967; Dannert & Jenko Reference Dannert and Jenko2005), and in the present paper we elaborate on the mathematical details of this calculation.
The Æ of a system is defined as the difference in energy between the ‘initial’ distribution function $f_i$![]() (i.e. the distribution function at time $t=0$
(i.e. the distribution function at time $t=0$![]() ), and the so-called ground state $f_g$
), and the so-called ground state $f_g$![]() (Lorenz Reference Lorenz1955; Gardner Reference Gardner1963). The latter is the distribution function which minimizes the energy, subject to constraints imposed by the Vlasov equation. We encapsulate the constraints that follow from Liouville's theorem in the following invariant:
(Lorenz Reference Lorenz1955; Gardner Reference Gardner1963). The latter is the distribution function which minimizes the energy, subject to constraints imposed by the Vlasov equation. We encapsulate the constraints that follow from Liouville's theorem in the following invariant:
where $\varTheta [x]$![]() is the Heaviside function, $\phi$
is the Heaviside function, $\phi$![]() is a scalar constant and $\boldsymbol {x}$
is a scalar constant and $\boldsymbol {x}$![]() are the phase-space coordinates, $(\boldsymbol {r},\boldsymbol {v})$
are the phase-space coordinates, $(\boldsymbol {r},\boldsymbol {v})$![]() . If the distribution function $f$
. If the distribution function $f$![]() evolves according to the Vlasov equation or any other equation that conserves phase-space volume, one can show that $H[f,\phi ]$
evolves according to the Vlasov equation or any other equation that conserves phase-space volume, one can show that $H[f,\phi ]$![]() is conserved for every $\phi \in \mathbb {R}$
is conserved for every $\phi \in \mathbb {R}$![]() (Helander Reference Helander2017). Furthermore, we define the energy of the distribution function as
(Helander Reference Helander2017). Furthermore, we define the energy of the distribution function as
where $\epsilon (\boldsymbol {x})$![]() is the energy of a particle (typically $mv^2/2$
is the energy of a particle (typically $mv^2/2$![]() , with m and $v$
, with m and $v$![]() being the particle mass and speed, respectively). With these definitions, the ground state can be denoted as the distribution function t minimizes the functional
being the particle mass and speed, respectively). With these definitions, the ground state can be denoted as the distribution function t minimizes the functional
where $\lambda (\phi )$![]() denotes a continuous set of Lagrange multipliers.
denotes a continuous set of Lagrange multipliers.
If one evaluates the variation of $W$![]() with respect to $f_g$
with respect to $f_g$![]() , and requires that the distribution function be a stationary point of the functional (that is $\delta W/\delta f_g=0$
, and requires that the distribution function be a stationary point of the functional (that is $\delta W/\delta f_g=0$![]() ), one finds that a ground state must be a function of energy alone
), one finds that a ground state must be a function of energy alone
Furthermore, if one considers the second variation with respect to $f_g$![]() and demands that this quantity be positive definite (so that the ground state is a local minimum of the functional), one finds that the ground state must be a decreasing function of energy
and demands that this quantity be positive definite (so that the ground state is a local minimum of the functional), one finds that the ground state must be a decreasing function of energy
One can also impose the condition that a set of adiabatic invariants, denoted by $\boldsymbol {y}$![]() , should be conserved (as in Helander Reference Helander2017, Reference Helander2020), thus adding more constraints than (1.4) and (1.5). The ground states are then functions satisfying
, should be conserved (as in Helander Reference Helander2017, Reference Helander2020), thus adding more constraints than (1.4) and (1.5). The ground states are then functions satisfying
From these criteria it is possible to derive an integro-differential equation for the ground state. For instance, it has been shown that, if we choose the magnetic moment $\mu$![]() and the parallel invariant $\mathcal {J}$
and the parallel invariant $\mathcal {J}$![]() as adiabatic invariants, the ground state $f_g(\epsilon,\mu,\mathcal {J})$
as adiabatic invariants, the ground state $f_g(\epsilon,\mu,\mathcal {J})$![]() must obey the following integro-differential equation (Helander Reference Helander2020):
must obey the following integro-differential equation (Helander Reference Helander2020):

Here, $w$![]() is a positive scalar which acts as a placeholder for the particle energy $\epsilon$
is a positive scalar which acts as a placeholder for the particle energy $\epsilon$![]() , $\psi$
, $\psi$![]() is the magnetic flux (i.e. the flux-surface label) and $\alpha$
is the magnetic flux (i.e. the flux-surface label) and $\alpha$![]() is the Clebsch angle, which locally define the magnetic field as $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$
is the Clebsch angle, which locally define the magnetic field as $\boldsymbol {B} = \boldsymbol {\nabla } \psi \times \boldsymbol {\nabla } \alpha$![]() (see D'haeseleer et al. (Reference D'haeseleer, Hitchon, Callen and Shohet2012), chapter 5). Equation (1.7) is relevant for most kinds of gyrokinetic turbulence in tokamaks and stellarators, since $\mu$
(see D'haeseleer et al. (Reference D'haeseleer, Hitchon, Callen and Shohet2012), chapter 5). Equation (1.7) is relevant for most kinds of gyrokinetic turbulence in tokamaks and stellarators, since $\mu$![]() and $\mathcal {J}$
and $\mathcal {J}$![]() are typically conserved quantities for trapped electrons in the case of microinstabilities and turbulence with wavelengths comparable to the ion gyroradius.
are typically conserved quantities for trapped electrons in the case of microinstabilities and turbulence with wavelengths comparable to the ion gyroradius.
In the literature, most numerical simulations of such phenomena are performed in the geometry of a slender flux tube aligned with the magnetic field, and in this limit (1.7) can be solved analytically. For the case of a vanishingly slender flux tube under the condition of omnigeneity, i.e. that the second adiabatic invariant $\mathcal {J}$![]() is independent of the Clebsch angle $\alpha$
is independent of the Clebsch angle $\alpha$![]() (i.e. $\partial \mathcal {J} / \partial \alpha = 0$
(i.e. $\partial \mathcal {J} / \partial \alpha = 0$![]() ), explicit expressions for the ground state and the Æ have been found (Helander Reference Helander2020). This derivation shows that a Maxwellian distribution function can only be a ground state if the magnetic field is omnigenous and if the electron diamagnetic drift frequency $\omega _*^T$
), explicit expressions for the ground state and the Æ have been found (Helander Reference Helander2020). This derivation shows that a Maxwellian distribution function can only be a ground state if the magnetic field is omnigenous and if the electron diamagnetic drift frequency $\omega _*^T$![]() does not exceed the bounce-averaged precession frequency $\omega _\alpha$
does not exceed the bounce-averaged precession frequency $\omega _\alpha$![]()
for all types of trapped-electron orbits in the flux tube. Here, the diamagnetic drift frequency is equal to
where $T$![]() is the temperature, $n$
is the temperature, $n$![]() is the number density, $\epsilon$
is the number density, $\epsilon$![]() is the particle energy and $q$
is the particle energy and $q$![]() is the particle charge. The criteria of (1.8) are met in quasi-isodynamic stellarators with the so-called maximum-$\mathcal {J}$
is the particle charge. The criteria of (1.8) are met in quasi-isodynamic stellarators with the so-called maximum-$\mathcal {J}$![]() property, and it has been shown from the (linear) gyrokinetic equations that these devices are indeed resilient against conventional density-gradient-driven trapped electron modes (TEMs) by Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander et al. (Reference Helander, Proll and Plunk2013). When these modes are stabilized, other, less virulent, instabilities become dominant instead (Helander & Plunk Reference Helander and Plunk2015; Plunk, Connor & Helander Reference Plunk, Connor and Helander2017; Costello et al. Reference Costello, Proll, Plunk, Pueschel and Alcusón2023).
property, and it has been shown from the (linear) gyrokinetic equations that these devices are indeed resilient against conventional density-gradient-driven trapped electron modes (TEMs) by Proll et al. (Reference Proll, Helander, Connor and Plunk2012) and Helander et al. (Reference Helander, Proll and Plunk2013). When these modes are stabilized, other, less virulent, instabilities become dominant instead (Helander & Plunk Reference Helander and Plunk2015; Plunk, Connor & Helander Reference Plunk, Connor and Helander2017; Costello et al. Reference Costello, Proll, Plunk, Pueschel and Alcusón2023).
In this paper we first extend the calculation of Æ to non-omnigenous flux tubes, which is of relevance since most stellarators are, in fact, not omnigenous. We first show that such a calculation is most easily done in flux tubes which have an elliptical cross-section. This calculation is described in § 2, where we also discuss how the Æ can be computed numerically. In § 3 we compare the numerically calculated Æ in a tokamak and various stellarators with the turbulent energy flux computed by the gyrokinetic code gene (Jenko et al. Reference Jenko, Dorland, Kotschenreuther and Rogers2000). These results were recently published in abbreviated form Mackenbach et al. (Reference Mackenbach, Proll and Helander2022), and here we provide full mathematical details. We furthermore investigate which types of trapped particles contribute most to Æ, and find that deeply trapped particles typically do so. We also establish that the dependence on the gradient strength is non-trivial and investigate this dependence in some depth. Finally, in § 4, we highlight our most important findings and discuss future directions for research.
2 The ground state and available energy in a flux tube
2.1 Allowable domains
In the calculation of the ground state, we restrict our attention to a subregion of the plasma which has the shape of a slender flux tube aligned with the magnetic field, allowing us to approximate the distribution function by its first-order Taylor expansion in the directions perpendicular to the field. Only then does it seem possible to solve the integro-differential ground-state equation (1.7) in general. Somewhat surprisingly, it turns out that the calculation is only possible if the cross-section of the flux tube is elliptical, as we shall now see.
We first introduce the following re-scaled coordinates:
Here, $\psi _0$![]() and $\alpha _0$
and $\alpha _0$![]() are the flux-surface label and field-line label of the magnetic field line defining the centre of the flux tube, and ${\mathrm \Delta} \psi$
are the flux-surface label and field-line label of the magnetic field line defining the centre of the flux tube, and ${\mathrm \Delta} \psi$![]() and ${\mathrm \Delta} \alpha$
and ${\mathrm \Delta} \alpha$![]() define its scale lengths in the $\psi$
define its scale lengths in the $\psi$![]() - and $\alpha$
- and $\alpha$![]() -directions, respectively. In contrast to the situation in most gyrokinetic simulations, the cross-section of the flux tube is not assumed to be rectangular. In these coordinates, we denote the first-order expansion of the distribution function $f$
-directions, respectively. In contrast to the situation in most gyrokinetic simulations, the cross-section of the flux tube is not assumed to be rectangular. In these coordinates, we denote the first-order expansion of the distribution function $f$![]() for fixed values of $\mu$
for fixed values of $\mu$![]() , $\mathcal {J}$
, $\mathcal {J}$![]() , and $t$
, and $t$![]() by
by
For a given smooth distribution function, this representation should always be sufficiently accurate in the limit of small ${\mathrm \Delta} \psi$![]() and ${\mathrm \Delta} \alpha$
and ${\mathrm \Delta} \alpha$![]() (i.e. for small enough $\psi - \psi _0$
(i.e. for small enough $\psi - \psi _0$![]() and $\alpha - \alpha _0$
and $\alpha - \alpha _0$![]() one can approximate $f \approx f_0 + (\psi - \psi _0) \partial _\psi f + (\alpha - \alpha _0) \partial _\alpha f$
one can approximate $f \approx f_0 + (\psi - \psi _0) \partial _\psi f + (\alpha - \alpha _0) \partial _\alpha f$![]() ), but there is no guarantee that the ground state corresponding to such a function can be similarly approximated by its linear expansion. Indeed, this turns out to be true, in general, only if the domain $\varOmega$
), but there is no guarantee that the ground state corresponding to such a function can be similarly approximated by its linear expansion. Indeed, this turns out to be true, in general, only if the domain $\varOmega$![]() in the $(x,y)$
in the $(x,y)$![]() -plane under consideration is elliptical. As already mentioned, phase-space volume conservation dictates that the following integral is independent of time for all values of $\phi$
-plane under consideration is elliptical. As already mentioned, phase-space volume conservation dictates that the following integral is independent of time for all values of $\phi$![]() :
:
In particular, this integral must be the same for the initial (given) distribution function and its corresponding ground state. We assume that both can be described by their linear approximations (2.2), whose gradients will, however, in general point in different directions (i.e. $\boldsymbol {\nabla }_\perp f \propto \hat {\boldsymbol {x}} f_x +\hat {\boldsymbol {y}} f_y$![]() can take on any value, with the hatted quantities denoting unit vectors). We thus require that the gradient of the ground state may point in an arbitrary direction and derive a constraint on the shape of $\varOmega$
can take on any value, with the hatted quantities denoting unit vectors). We thus require that the gradient of the ground state may point in an arbitrary direction and derive a constraint on the shape of $\varOmega$![]() from this condition.
from this condition.
It is useful to define a rotated coordinate system $(x,y)\mapsto (\tilde {x},\tilde {y})$![]()

such that $f$![]() assumes its smallest value, $f_\textrm {min}$
assumes its smallest value, $f_\textrm {min}$![]() , at $\tilde x = 0$
, at $\tilde x = 0$![]() and the gradient of $f$
and the gradient of $f$![]() points in the direction of $\tilde x$
points in the direction of $\tilde x$![]()
In such a coordinate system the domain rotates as the function evolves, whilst fixing the minimal values of $x$![]() and $y$
and $y$![]() to $\tilde {x}=\tilde {y}=0$
to $\tilde {x}=\tilde {y}=0$![]() , and this coordinate system will aid us in making statements about this domain shape. The initial state and the ground state thus correspond to two different values of $\vartheta$
, and this coordinate system will aid us in making statements about this domain shape. The initial state and the ground state thus correspond to two different values of $\vartheta$![]() . The width of the domain $\varOmega$
. The width of the domain $\varOmega$![]() in the $\tilde x$
in the $\tilde x$![]() -direction is denoted by $2D(\vartheta )$
-direction is denoted by $2D(\vartheta )$![]() , so that the maximum value of $f$
, so that the maximum value of $f$![]() becomes $f_\mathrm {max} = f_\mathrm {min} + 2 D f_{\tilde {x}}$
becomes $f_\mathrm {max} = f_\mathrm {min} + 2 D f_{\tilde {x}}$![]() , and the distribution function may be written as
, and the distribution function may be written as
where we note that $f_\mathrm {min}$![]() and $f_\mathrm {max}$
and $f_\mathrm {max}$![]() depend only on $\mu$
depend only on $\mu$![]() and $\mathcal {J}$
and $\mathcal {J}$![]() and are thus independent of $\vartheta$
and are thus independent of $\vartheta$![]() .
.
We now return to the problem at hand, codified by (2.3). The argument of the Heaviside function vanishes in the new coordinate system when
Let us now consider a value of $\phi$![]() very close to $f_\mathrm {min}$
very close to $f_\mathrm {min}$![]() , i.e. $\phi = f_\mathrm {min} + |\epsilon |$
, i.e. $\phi = f_\mathrm {min} + |\epsilon |$![]() with $|\epsilon | \rightarrow 0^+$
with $|\epsilon | \rightarrow 0^+$![]() . Equation (2.7) now reduces to $\tilde {x}_\epsilon = 2D|\epsilon |/(f_\mathrm {max}-f_\mathrm {min})$
. Equation (2.7) now reduces to $\tilde {x}_\epsilon = 2D|\epsilon |/(f_\mathrm {max}-f_\mathrm {min})$![]() . The integral in (2.3) is equal to the area of the subdomain of $\varOmega$
. The integral in (2.3) is equal to the area of the subdomain of $\varOmega$![]() over which $f \le \phi$
over which $f \le \phi$![]() , i.e. the coloured region in figure 1. In the limit $\tilde {x}_\epsilon \ll D$
, i.e. the coloured region in figure 1. In the limit $\tilde {x}_\epsilon \ll D$![]() , the radius of curvature, $R$
, the radius of curvature, $R$![]() , of the domain boundary in the region $\tilde x < \tilde x_\epsilon$
, of the domain boundary in the region $\tilde x < \tilde x_\epsilon$![]() is approximately constant (if the boundary is sufficiently smooth). Hence, we may approximate the integral by instead considering the area of a circular segment with the same radius of curvature $R$
is approximately constant (if the boundary is sufficiently smooth). Hence, we may approximate the integral by instead considering the area of a circular segment with the same radius of curvature $R$![]()

where we have used the equation for a circle $\tilde {y}^2 = R^2 - (\tilde {x} - R)^2$![]() . The next step is to realize that, as the distribution function evolves, its gradient may point in any direction in the $(x,y)$
. The next step is to realize that, as the distribution function evolves, its gradient may point in any direction in the $(x,y)$![]() -plane, so that the angle $\vartheta$
-plane, so that the angle $\vartheta$![]() may assume any value. A sketch of the domain at a different orientation is also given in figure 1. Both $D$
may assume any value. A sketch of the domain at a different orientation is also given in figure 1. Both $D$![]() and $R$
and $R$![]() depend on $\vartheta$
depend on $\vartheta$![]() , but they are not independent. Indeed, from (2.3) we have
, but they are not independent. Indeed, from (2.3) we have
where we have used the equation for the area found in (2.8). In particular, the radius of curvature is the same at the two extremal locations $\tilde {x}=0$![]() and $\tilde {x}=2D$
and $\tilde {x}=2D$![]() , since a rotation of ${\rm \pi}$
, since a rotation of ${\rm \pi}$![]() leaves $D$
leaves $D$![]() unchanged. Moreover, on purely geometrical grounds there is a relation between the second derivative of the domain width and the curvature, as shown in Appendix A,
unchanged. Moreover, on purely geometrical grounds there is a relation between the second derivative of the domain width and the curvature, as shown in Appendix A,
Using the constancy of $RD^3$![]() , we find that
, we find that

As shown in Appendix A, this differential equation has the general solution
implying that the radius of curvature becomes
The radius of curvature for an ellipse is of the exact same form as (2.13) (as shown in Appendix A), implying that $\varOmega$![]() must be elliptical. We have thus found that the only domain shape in which Liouville's theorem can generally be satisfied is a slanted ellipse, if the distribution function is to be approximated by its first-order Taylor expansion in the coordinates perpendicular to the magnetic field.
must be elliptical. We have thus found that the only domain shape in which Liouville's theorem can generally be satisfied is a slanted ellipse, if the distribution function is to be approximated by its first-order Taylor expansion in the coordinates perpendicular to the magnetic field.

Figure 1. A sketch of the area, coloured red, as a subset of the entire domain $\varOmega$![]() . Done at two different times, so that the orientation of the domain $\varOmega$
. Done at two different times, so that the orientation of the domain $\varOmega$![]() is different.
is different.
2.2 The ground state and the available energy
As shown in the previous section the domain has to be a slanted ellipse, and here we shall derive what the ground state and Æ is in such a system. To this end, let us first realize that it is sufficient to calculate the Æ in an unslanted ellipse, which in the coordinates $x$![]() and $y$
and $y$![]() of the previous section has the equation
of the previous section has the equation
with $a \leq b$![]() . We may then apply a rotation operator to find the result of any slanted ellipse. Let us start, then, by considering (1.7) and one must evaluate integrals of the form
. We may then apply a rotation operator to find the result of any slanted ellipse. Let us start, then, by considering (1.7) and one must evaluate integrals of the form
where $h(\psi,\alpha )$![]() is an arbitrary smooth function that vanishes in the centre of the domain, $h(0,0)=0$
is an arbitrary smooth function that vanishes in the centre of the domain, $h(0,0)=0$![]() . This condition has to do with the fact that a constant Maxwellian is the ground state corresponding to an initial condition without gradients. As such, to lowest order the difference between the Maxwellian and the ground state should vanish, implying that $h(0,0)=0$
. This condition has to do with the fact that a constant Maxwellian is the ground state corresponding to an initial condition without gradients. As such, to lowest order the difference between the Maxwellian and the ground state should vanish, implying that $h(0,0)=0$![]() for the functions appearing in (1.7). Since we take the flux tube to be slender, we approximate the function $h$
for the functions appearing in (1.7). Since we take the flux tube to be slender, we approximate the function $h$![]() as
as
We next define the vector $\boldsymbol {p} = ( x, y )$![]() , so that one can write the linear expansion of $h$
, so that one can write the linear expansion of $h$![]() as
as
where we have defined $\boldsymbol {n} \equiv \partial _{\boldsymbol {p}} h/ |\partial _{\boldsymbol {p}} h|$![]() , and derivatives of $h$
, and derivatives of $h$![]() are evaluated at the centre of the flux tube. Equation (2.15) then becomes
are evaluated at the centre of the flux tube. Equation (2.15) then becomes
The integral measures the length of the line where $h=0$![]() in the domain, which may be found as follows. We realize that this line satisfies the equation
in the domain, which may be found as follows. We realize that this line satisfies the equation
where we have used the notation $h_x \equiv \partial _x h$![]() . We may now find its intersection with the ellipse given by (2.14), and one may readily verify that the points of intersection $(x,y)$
. We may now find its intersection with the ellipse given by (2.14), and one may readily verify that the points of intersection $(x,y)$![]() satisfy the equation
satisfy the equation
and the integral thus becomes

Our final step is to rotate the domain, which is equivalent to rotating the vector $\partial _{\boldsymbol {p}} h$![]() , for which one can use the rotation mapping
, for which one can use the rotation mapping
where $\vartheta$![]() measures the angle of rotation. Combining results of (2.21) and (2.22), we find
measures the angle of rotation. Combining results of (2.21) and (2.22), we find

where the eccentricity $e \in [0,1)$![]() is defined as $e^2 \equiv 1 - a^2/b^2$
is defined as $e^2 \equiv 1 - a^2/b^2$![]() . We are now in a position to evaluate the ground state; first choose the initial distribution function to be a Maxwellian (as usually done in gyrokinetic simulations)
. We are now in a position to evaluate the ground state; first choose the initial distribution function to be a Maxwellian (as usually done in gyrokinetic simulations)

Here, $n(\psi )$![]() is the number density, $m$
is the number density, $m$![]() is the electron mass and $T(\psi )$
is the electron mass and $T(\psi )$![]() is the electron temperature. The spatial derivatives of the distribution and energy function can be related to the bounce-averaged precession frequencies of the electron orbits (as shown in Appendix B)
is the electron temperature. The spatial derivatives of the distribution and energy function can be related to the bounce-averaged precession frequencies of the electron orbits (as shown in Appendix B)
Here, quantities with the subscript zero are quantities that are evaluated at the centre of the flux tube, $q$![]() is the electron charge, $\omega _\psi$
is the electron charge, $\omega _\psi$![]() is the drift (precession) frequency in the $\psi$
is the drift (precession) frequency in the $\psi$![]() direction, $\omega _\alpha$
direction, $\omega _\alpha$![]() is the corresponding frequency in the $\alpha$
is the corresponding frequency in the $\alpha$![]() direction and $\omega _*^T$
direction and $\omega _*^T$![]() is the electron diamagnetic frequency. With these expressions, the numerator in (1.7) for the ground state becomes
is the electron diamagnetic frequency. With these expressions, the numerator in (1.7) for the ground state becomes
The denominator of (1.7) can be calculated in a similar manner. We conclude that the ground-state distribution function has the following derivative:

Since the right-hand side is negative, the solution decreases with increasing energy, which is a requirement for any ground state. In the limit of omnigeneity (thus $\omega _\psi = 0$![]() ) one may verify that the terms involving $\mathcal {E}_\vartheta$
) one may verify that the terms involving $\mathcal {E}_\vartheta$![]() cancel, and one retrieves the expression previously found by Helander (Reference Helander2020). To evaluate the Æ, we must find the difference in energy between the initial distribution function and the ground state
cancel, and one retrieves the expression previously found by Helander (Reference Helander2020). To evaluate the Æ, we must find the difference in energy between the initial distribution function and the ground state
Here, $\sqrt {g}$![]() denotes the phase-space Jacobian, which reduces to $\sqrt {g}= 4 {\rm \pi}/ m^2$
denotes the phase-space Jacobian, which reduces to $\sqrt {g}= 4 {\rm \pi}/ m^2$![]() (Helander Reference Helander2017). Moreover, $f_i$
(Helander Reference Helander2017). Moreover, $f_i$![]() and $f_g$
and $f_g$![]() can be approximated by their Taylor expansions
can be approximated by their Taylor expansions
It is useful to realize that the total number of particles within the domain for each pair of $\mu$![]() and $\mathcal {J}$
and $\mathcal {J}$![]() is conserved, giving
is conserved, giving
which in turn implies that the Æ can be calculated, to leading order, as
The integration across $x$![]() and $y$
and $y$![]() is readily carried out by rotating the function $x^2$
is readily carried out by rotating the function $x^2$![]() or $y^2$
or $y^2$![]() by some angle, and integrating this function over the domain whose boundary is given in (2.14). This may be readily calculated as
by some angle, and integrating this function over the domain whose boundary is given in (2.14). This may be readily calculated as
Our final step is to impose that this area of the ellipse is the same area as the unit circle ($a b = 1$![]() ), which may be achieved by an appropriate choice of ${\mathrm \Delta} \psi$
), which may be achieved by an appropriate choice of ${\mathrm \Delta} \psi$![]() and/or ${\mathrm \Delta} \alpha$
and/or ${\mathrm \Delta} \alpha$![]() . We thus have
. We thus have

Again, in the limit $\omega _\psi \rightarrow 0$![]() , the Æ reduces to the previously found expression (Helander Reference Helander2020).Footnote 1 The above equation is the central result of this paper, and may be interpreted as the most general result of the local available energy of trapped particles. To simplify further steps of the calculation, we shall specialize to the case in which the cross-section is circular in $(x,y)$
, the Æ reduces to the previously found expression (Helander Reference Helander2020).Footnote 1 The above equation is the central result of this paper, and may be interpreted as the most general result of the local available energy of trapped particles. To simplify further steps of the calculation, we shall specialize to the case in which the cross-section is circular in $(x,y)$![]() , which implies $e = 0$
, which implies $e = 0$![]() . Note that this does not imply that the cross-section is also circular in $(\psi,\alpha )$
. Note that this does not imply that the cross-section is also circular in $(\psi,\alpha )$![]() -space: in these coordinates it is still an ellipse whose semi-major and semi-minor axes lie on lines of constant $\psi$
-space: in these coordinates it is still an ellipse whose semi-major and semi-minor axes lie on lines of constant $\psi$![]() and $\alpha$
and $\alpha$![]() . This furthermore has as a consequence that the various functions dependent on the angle of rotation and eccentricity simplify to $\mathcal {E}_\vartheta ^2 = 0$
. This furthermore has as a consequence that the various functions dependent on the angle of rotation and eccentricity simplify to $\mathcal {E}_\vartheta ^2 = 0$![]() , $\hat {\mathcal {E}}_{\vartheta }^2=\check {\mathcal {E}}_{\vartheta }^2 = 1$
, $\hat {\mathcal {E}}_{\vartheta }^2=\check {\mathcal {E}}_{\vartheta }^2 = 1$![]() , simplifying the calculations significantly. If the eccentricity is non-zero but small, the leading-order correction is of order $\mathcal {O}(e^2)$
, simplifying the calculations significantly. If the eccentricity is non-zero but small, the leading-order correction is of order $\mathcal {O}(e^2)$![]() .
.
2.3 Making the integral dimensionless
We proceed by making the expression for Æ dimensionless. We first normalize the magnetic field to some reference strength $B_0$![]()
Here, $B(\ell )$![]() is the magnetic-field strength as a function of the arc length $\ell$
is the magnetic-field strength as a function of the arc length $\ell$![]() along the flux tube. As in neoclassical transport theory (see Helander & Sigmar (Reference Helander and Sigmar2005), chapter 7), it is useful to perform a change of variables, $(\mu,\mathcal {J}) \mapsto (\lambda, z)$
along the flux tube. As in neoclassical transport theory (see Helander & Sigmar (Reference Helander and Sigmar2005), chapter 7), it is useful to perform a change of variables, $(\mu,\mathcal {J}) \mapsto (\lambda, z)$![]() , with
, with
In these variables, the second adiabatic invariant becomes
if the electric field parallel to $\boldsymbol {B}$![]() vanishes. Here, we have introduced a shorthand for the integration domain, which is given by the interval in $\ell$
vanishes. Here, we have introduced a shorthand for the integration domain, which is given by the interval in $\ell$![]() between two consecutive bounce points
between two consecutive bounce points
The derivatives of $\mathcal {J}$![]() can be used to find bounce-averaged precession frequencies, as shown in Appendix B. We now define dimensionless precession frequencies, which are the dimensionless equivalents of the precession and drift frequencies in (2.25),
can be used to find bounce-averaged precession frequencies, as shown in Appendix B. We now define dimensionless precession frequencies, which are the dimensionless equivalents of the precession and drift frequencies in (2.25),
Finally, one needs to account for the change in the volume element from $(\mu,\mathcal {J}) \mapsto (z,\lambda )$![]() . The Jacobian of this transformation, which we denote by $G^{1/2}$
. The Jacobian of this transformation, which we denote by $G^{1/2}$![]() , is
, is

where $L$![]() denotes the length of the magnetic-field line. We are now in a position to express the Æ in terms of these new variables
denotes the length of the magnetic-field line. We are now in a position to express the Æ in terms of these new variables

Here, we have introduced a summation over all bounce wells corresponding to a given value of $\lambda$![]() , and we have introduced the nonlinear function
, and we have introduced the nonlinear function

The prefactor in front of the integral in (2.40) is readily interpreted. The factor ${\rm \pi} n_0 {\mathrm \Delta} \psi {\mathrm \Delta} \alpha L / \bar {B}$![]() is roughly the amount of particles residing in our flux tube, which we will call $N$
is roughly the amount of particles residing in our flux tube, which we will call $N$![]() , and hence the Æ is proportional to the total energy of these particles, $NT_0$
, and hence the Æ is proportional to the total energy of these particles, $NT_0$![]() . It is furthermore relatively straightforward to show that the integrand of (2.40) is always positive definite, as follows from the expression
. It is furthermore relatively straightforward to show that the integrand of (2.40) is always positive definite, as follows from the expression

Since

the integrand in (2.40) must be positive definite, and so is therefore the Æ. It is also clear from this argument that even a small degree of non-omnigeneity in the magnetic-field geometry endows available energy to a plasma which otherwise has none, for the right-hand side of (2.43) is always positive if $\hat {\omega }_\psi \ne 0$![]() . In other words, a Maxwellian can only be a ground state if the magnetic field is omnigenous (Helander Reference Helander2020).
. In other words, a Maxwellian can only be a ground state if the magnetic field is omnigenous (Helander Reference Helander2020).
Our final step is to find the fraction of energy that is available. The thermal energy of a plasma in a flux tube can readily be calculated to leading order in the perpendicular coordinates as
Hence, the fraction of energy that is available is equal to

2.4 Relating available energy to turbulence
Our next step is to relate Æ to typical turbulence quantities, but there is basic difficulty having to do with the question of how these scale with the size of the system. There exist types of turbulence which depend on the size and shape of the domain in which it takes place, but we are mainly interested in turbulence for which this is not the case if the domain is large enough. We will refer to such turbulence as ‘local’. In a sufficiently resolved simulation, the correlation length of local turbulence will be smaller than the computational domain. Furthermore, if we expect Æ to encapsulate information about local turbulence, it should act as an extensive thermodynamic variable and thus scale linearly with the simulation volume. In expression (2.40), however, we see that under the replacement $({\mathrm \Delta} \psi, {\mathrm \Delta} \alpha ) \mapsto C({\mathrm \Delta} \psi, {\mathrm \Delta} \alpha )$![]() the Æ transforms as $A \mapsto C^4 A$
the Æ transforms as $A \mapsto C^4 A$![]() (as $\hat {\omega }_\psi$
(as $\hat {\omega }_\psi$![]() and $\hat {\omega }_\alpha$
and $\hat {\omega }_\alpha$![]() scale linearly with $C$
scale linearly with $C$![]() ). The underlying physical reason is that the Æ measures the maximum amount of energy that can be released by redistributing plasma over the entire domain, which scales as the volume of the domain (${\sim }C^2$
). The underlying physical reason is that the Æ measures the maximum amount of energy that can be released by redistributing plasma over the entire domain, which scales as the volume of the domain (${\sim }C^2$![]() ) multiplied by the square of the variation of the distribution function over the domain (${\sim }C^2$
) multiplied by the square of the variation of the distribution function over the domain (${\sim }C^2$![]() ), see Helander (Reference Helander2017). Local turbulence, however, is only able to redistribute plasma over some finite length scale comparable to the correlation length. The latter can be different in the two directions perpendicular to the magnetic field, and the appropriate choice for the domain size over which the system can redistribute particles are these length scales in the $\psi$
), see Helander (Reference Helander2017). Local turbulence, however, is only able to redistribute plasma over some finite length scale comparable to the correlation length. The latter can be different in the two directions perpendicular to the magnetic field, and the appropriate choice for the domain size over which the system can redistribute particles are these length scales in the $\psi$![]() - and $\alpha$
- and $\alpha$![]() -directions.Footnote 2 Let us denote these length scales by ${\mathrm \Delta} \psi _{A}$
-directions.Footnote 2 Let us denote these length scales by ${\mathrm \Delta} \psi _{A}$![]() and ${\mathrm \Delta} \alpha _{A}$
and ${\mathrm \Delta} \alpha _{A}$![]() , respectively. For fixed ${\mathrm \Delta} \psi _{A}$
, respectively. For fixed ${\mathrm \Delta} \psi _{A}$![]() and ${\mathrm \Delta} \alpha _{A}$
and ${\mathrm \Delta} \alpha _{A}$![]() we see that (2.45) is indeed independent of the domain size, and hence the total Æ acts as a thermodynamic variable.
we see that (2.45) is indeed independent of the domain size, and hence the total Æ acts as a thermodynamic variable.
To choose these length scales appropriately, we define radial and binormal coordinates in units of length by

where $\psi _\mathrm {tot}$![]() is the total toroidal flux passing through the last closed flux surface, and $r_0 = a \sqrt {\psi _0/\psi _\mathrm {tot}}$
is the total toroidal flux passing through the last closed flux surface, and $r_0 = a \sqrt {\psi _0/\psi _\mathrm {tot}}$![]() . In terms of these coordinates, we require that the length scales are of the form
. In terms of these coordinates, we require that the length scales are of the form
where $\rho$![]() is the Larmor radius, and $C_r$
is the Larmor radius, and $C_r$![]() and $C_y$
and $C_y$![]() are functions of order $\mathcal {O}(\rho ^0)$
are functions of order $\mathcal {O}(\rho ^0)$![]() , which can depend on the equilibrium parameters such as the rotational transform $\iota$
, which can depend on the equilibrium parameters such as the rotational transform $\iota$![]() or the magnetic shear $s$
or the magnetic shear $s$![]() . We note that, by choosing proportionality to the gyroradius, the Æ becomes proportional to the expansion parameter $(\rho _*)^2 \equiv (\rho /L_\mathrm {ref})^2$
. We note that, by choosing proportionality to the gyroradius, the Æ becomes proportional to the expansion parameter $(\rho _*)^2 \equiv (\rho /L_\mathrm {ref})^2$![]() , with $L_\mathrm {ref}$
, with $L_\mathrm {ref}$![]() being some equilibrium length scale. This is because $\omega _\alpha$
being some equilibrium length scale. This is because $\omega _\alpha$![]() and $\omega _\psi$
and $\omega _\psi$![]() are set by the equilibrium and exhibit an $L_\mathrm {ref}^{-1}$
are set by the equilibrium and exhibit an $L_\mathrm {ref}^{-1}$![]() dependence. The ratio of $C_r/C_s$
dependence. The ratio of $C_r/C_s$![]() is a measure of anisotropy; if $C_r/C_s=1$
is a measure of anisotropy; if $C_r/C_s=1$![]() the correlation length is similar in the radial and binormal direction. Conversely, if there are large radial streamers present in a system one could reasonably expect $C_r/C_s \gg 1$
the correlation length is similar in the radial and binormal direction. Conversely, if there are large radial streamers present in a system one could reasonably expect $C_r/C_s \gg 1$![]() . As such, it is unclear a priori what a proper length scaleis for both $C_r$
. As such, it is unclear a priori what a proper length scaleis for both $C_r$![]() and $C_s$
and $C_s$![]() , as it will in general depend on the specific structure of the turbulence. For the rest of the investigation, we shall make use of the simplest possible ansatz for $C_r$
, as it will in general depend on the specific structure of the turbulence. For the rest of the investigation, we shall make use of the simplest possible ansatz for $C_r$![]() and $C_s$
and $C_s$![]() : we shall take them to be equal and independent of equilibrium parameters, i.e.
: we shall take them to be equal and independent of equilibrium parameters, i.e.
Finally, to facilitate a comparison with nonlinear gyrokinetic turbulence simulations, we define a dimensionless Æ
Note that this choice for $\hat {A}$![]() differs from the one used in Mackenbach et al. (Reference Mackenbach, Proll and Helander2022), (up to a constant prefactor) by the factor $(\int \hat {B}^{-1} \,\mathrm {d} \ell / L)^{-1}$
differs from the one used in Mackenbach et al. (Reference Mackenbach, Proll and Helander2022), (up to a constant prefactor) by the factor $(\int \hat {B}^{-1} \,\mathrm {d} \ell / L)^{-1}$![]() . In the results which are to be presented the inclusion or exclusion of this factor does not alter the results significantly. In devices with large variation in the magnetic-field strength, however, this factor can change $\hat {A}$
. In the results which are to be presented the inclusion or exclusion of this factor does not alter the results significantly. In devices with large variation in the magnetic-field strength, however, this factor can change $\hat {A}$![]() to a greater extent. Since the above expression for $\hat {A}$
to a greater extent. Since the above expression for $\hat {A}$![]() is the fraction of energy that is available in the flux tube, we find that this definition is more natural. Finally, we denote some important dependencies of $\hat {A}$
is the fraction of energy that is available in the flux tube, we find that this definition is more natural. Finally, we denote some important dependencies of $\hat {A}$![]() . Firstly, upon rescaling $(C_r,C_s) \mapsto C (C_r,C_s)$
. Firstly, upon rescaling $(C_r,C_s) \mapsto C (C_r,C_s)$![]() by a factor $C$
by a factor $C$![]() , the Æ scales as $\hat {A} \mapsto C^2 \hat {A}$
, the Æ scales as $\hat {A} \mapsto C^2 \hat {A}$![]() . A rescaling of $C_r$
. A rescaling of $C_r$![]() and $C_s$
and $C_s$![]() may thus have a significant impact on the Æ. Furthermore, if one increases the magnitude of $C_s$
may thus have a significant impact on the Æ. Furthermore, if one increases the magnitude of $C_s$![]() for fixed $C_r$
for fixed $C_r$![]() , (2.43) implies that the Æ will increase as well. In general, one should thus expect results to be dependent on the choice of $C_r$
, (2.43) implies that the Æ will increase as well. In general, one should thus expect results to be dependent on the choice of $C_r$![]() and $C_s$
and $C_s$![]() , and the choice of $C_r=C_s=1$
, and the choice of $C_r=C_s=1$![]() should be interpreted as the simplest possible model for these functions.
should be interpreted as the simplest possible model for these functions.
3 Results
3.1 Comparison with nonlinear gyrokinetics
A routine for calculating the Æ has been implemented in pythonFootnote 3 , with numerical routines discussed in Mackenbach et al. (Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023). The calculations are very fast; in the current implementation less than a CPU minute is required to obtain a sufficiently resolved result. We compare the Æ of various devices with saturated turbulent energy fluxes calculated by nonlinear flux-tube simulations in the gene code. More specifically we compare the dimensionless Æ, as defined in (2.49), with the normalized saturated radial energy flux $\hat {Q}_\textrm {sat}$![]() defined as
defined as
Here, $Q_e(t)$![]() is the instantaneous total radial electron energy flux across the tube as a function of time, and $t_\textrm {sat}$
is the instantaneous total radial electron energy flux across the tube as a function of time, and $t_\textrm {sat}$![]() denotes the time span of the simulation in which the turbulence is saturated, which should exceed the time in which the energy flux saturates. The simulation set consists of both density-gradient- and electron-temperature-gradient-driven, collisionless, electrostatic turbulence simulations, the majority of which have been discussed in Proll et al. (Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). The ion temperature gradient is chosen to be zero in order to avoid effects from ion temperature gradient modes, which are not accounted for by our model since only the Æ of electrons is considered. Furthermore, collisions are negligible in sufficiently hot plasmas, and may not alter the Æ significantly as long as conservation of $\mu$
denotes the time span of the simulation in which the turbulence is saturated, which should exceed the time in which the energy flux saturates. The simulation set consists of both density-gradient- and electron-temperature-gradient-driven, collisionless, electrostatic turbulence simulations, the majority of which have been discussed in Proll et al. (Reference Proll, Plunk, Faber, Görler, Helander, McKinney, Pueschel, Smith and Xanthopoulos2022). The ion temperature gradient is chosen to be zero in order to avoid effects from ion temperature gradient modes, which are not accounted for by our model since only the Æ of electrons is considered. Furthermore, collisions are negligible in sufficiently hot plasmas, and may not alter the Æ significantly as long as conservation of $\mu$![]() and $\mathcal {J}$
and $\mathcal {J}$![]() holds on time scales comparable to the inverse instability frequency (Kolmes & Fisch Reference Kolmes and Fisch2020). Finally, since electromagnetic effects only become relevant at relatively high normalized plasma pressure, they are neglected (Püschel Reference Püschel2009; Aleynikova et al. Reference Aleynikova, Zocco, Xanthopoulos, Helander and Nührenberg2018).
holds on time scales comparable to the inverse instability frequency (Kolmes & Fisch Reference Kolmes and Fisch2020). Finally, since electromagnetic effects only become relevant at relatively high normalized plasma pressure, they are neglected (Püschel Reference Püschel2009; Aleynikova et al. Reference Aleynikova, Zocco, Xanthopoulos, Helander and Nührenberg2018).
The results of this analysis are plotted in figure 2, which exhibits a close correlation between turbulent transport and Æ in one tokamak and various stellarators for various values of the density gradient as indicated in colour. The gradients are expressed in terms of $L_\textrm {ref}/L_n$![]() , where $L_n$
, where $L_n$![]() is the length scale of the density gradient defined as $L_n= -n/(\mathrm {d} n / \mathrm {d} r)$
is the length scale of the density gradient defined as $L_n= -n/(\mathrm {d} n / \mathrm {d} r)$![]() , with $r$
, with $r$![]() being the minor radial coordinate. Furthermore, two grey points are included which have no density gradient and an electron temperature gradient of $L_{T}= -T/(\mathrm {d} T / \mathrm {d} r) = 3$
being the minor radial coordinate. Furthermore, two grey points are included which have no density gradient and an electron temperature gradient of $L_{T}= -T/(\mathrm {d} T / \mathrm {d} r) = 3$![]() .Footnote 4 A peculiarity occurs in the data set from the high-mirror magnetic configuration in W7-X, at $L_\textrm {ref}/L_n=2$
.Footnote 4 A peculiarity occurs in the data set from the high-mirror magnetic configuration in W7-X, at $L_\textrm {ref}/L_n=2$![]() . Surprisingly, this data point has a lower energy flux than the $L_\textrm {ref}/L_n=1$
. Surprisingly, this data point has a lower energy flux than the $L_\textrm {ref}/L_n=1$![]() case, which is counter-intuitive as stronger gradients usually lead to more turbulence. It is postulated that this peculiar behaviour is due to a difference in the dominant instability, leading to the difference in transport. At low gradients, the ion-driven TEM (iTEM) may be dominant in W7-X High Mirror (HM), which unlike the ordinary TEM derives its energy from the ions (Plunk et al. Reference Plunk, Connor and Helander2017). At high gradients, it is expected that the universal instability starts to dominate transport (Helander & Plunk Reference Helander and Plunk2015; Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015; Costello et al. Reference Costello, Proll, Plunk, Pueschel and Alcusón2023). Neither of these instabilities derive energy from the trapped electrons, and it is not self-evident that the Æ of trapped electrons should be correlated with turbulent transport in this regime.
case, which is counter-intuitive as stronger gradients usually lead to more turbulence. It is postulated that this peculiar behaviour is due to a difference in the dominant instability, leading to the difference in transport. At low gradients, the ion-driven TEM (iTEM) may be dominant in W7-X High Mirror (HM), which unlike the ordinary TEM derives its energy from the ions (Plunk et al. Reference Plunk, Connor and Helander2017). At high gradients, it is expected that the universal instability starts to dominate transport (Helander & Plunk Reference Helander and Plunk2015; Landreman, Antonsen & Dorland Reference Landreman, Antonsen and Dorland2015; Costello et al. Reference Costello, Proll, Plunk, Pueschel and Alcusón2023). Neither of these instabilities derive energy from the trapped electrons, and it is not self-evident that the Æ of trapped electrons should be correlated with turbulent transport in this regime.

Figure 2. A scatter plot showing the normalized Æ for a range of stellarator and tokamak plasmas and the average nonlinear saturated turbulent radial energy flux from gyrokinetic simulations of these plasmas. The different points refer to different density gradients, as indicated by the colour, and to different devices. The devices that are used in this analysis are the tokamak DIII-D, the Helically Symmetric eXperiment (HSX) and the W7-X stellarator in both high-mirror configuration (HM) and standard configuration (SC). The straight black line shows the least-squares fit, which results in the power law $\ln Q_\textrm {sat} \propto (1.5 \pm 0.1) \ln A$![]() .
.
A power law is found by fitting a straight line to the log–log plot given in figure 2, where we have excluded the grey points from the fitting procedure. The fit results in
This relation is of interest, as it can be motivated in the following manner. The electron energy flux density in the direction of $\boldsymbol {\nabla } x$![]() is defined as
is defined as
Here, $\boldsymbol {v}_D$![]() is the gyro-averaged drift velocity, and $f_{e1}$
is the gyro-averaged drift velocity, and $f_{e1}$![]() is the fluctuating part of the electron distribution function (Görler Reference Görler2010). We go on to crudely estimate this flux as
is the fluctuating part of the electron distribution function (Görler Reference Görler2010). We go on to crudely estimate this flux as
where the angular brackets denotes an average over the simulated volume. The integral in this expression is bounded by the Æ, and hence we set $\int \epsilon f_{e1} \,\mathrm {d}\boldsymbol {x} \sim A$![]() . The average of the squared drift velocity,
. The average of the squared drift velocity,
is proportional to the gyrokinetic energy of the electric field. Since the sum total of the thermal and this field energy should be conserved (Helander Reference Helander2017), this field energy is also bounded by the Æ. We thus estimate that $\langle \boldsymbol {v}_E^2 \rangle \sim A$![]() , which gives
, which gives
in agreement with the observed power law. We have furthermore tried different conditions for particles which cross the computational boundary (Mackenbach et al. Reference Mackenbach, Duff, Gerard, Proll, Helander and Hegna2023), and we find that the results are resilient against these such variations.
The two grey points lie significantly below the black line in figure 2. A possible reason may be that all the other points refer to plasmas with a density gradient, in which there is, in principle, Æ in both the electron and ion populations (although we have only considered the electons). In contrast, for the grey points correspond to plasmas with an electron gradient alone, implying that the Æ from the ions vanishes identically. There is thus less energy to drive turbulence in this case.
3.2 The distribution of Æ
We now go on to investigate how different trapped particle orbits contribute to the Æ. In order to do so, we define an Æ per trapping well, namely
so that $\int \sum _{\mathrm {wells}} \hat {A}_\lambda \,\mathrm {d} \lambda = \hat {A}$![]() . For any given value of $\lambda$
. For any given value of $\lambda$![]() , this quantity can be calculated separately for each trapping well. The bounce points associated with each $\lambda$
, this quantity can be calculated separately for each trapping well. The bounce points associated with each $\lambda$![]() , which we denote by $\theta _b$
, which we denote by $\theta _b$![]() (with $\theta$
(with $\theta$![]() being the poloidal angle, our field-line following coordinate), satisfy
being the poloidal angle, our field-line following coordinate), satisfy
One can then draw a straight line between the two bounce points of a bounce well, and colour that line according to its associated $A_\lambda$![]() . One can furthermore investigate $\hat {\omega }_\alpha$
. One can furthermore investigate $\hat {\omega }_\alpha$![]() and $\hat {\omega }_\psi$
and $\hat {\omega }_\psi$![]() as a function of their bounce points. This can be done by realizing that both $\hat {\omega }_\alpha$
as a function of their bounce points. This can be done by realizing that both $\hat {\omega }_\alpha$![]() and $\hat {\omega }_\psi$
and $\hat {\omega }_\psi$![]() can be mapped onto their bounce points using (3.8), and one can thus investigate how their values depend on the bounce points.
can be mapped onto their bounce points using (3.8), and one can thus investigate how their values depend on the bounce points.
A plot displaying the properties of (3.7) in this way is shown in figure 3 for the case of the DIII-D tokamak with a normalizeddensity gradient $L_\mathrm {ref}/L_n = 3$![]() . Additionally, the binormal and radial drifts are shown as dashed green and dash-dotted blue lines, respectively. For convenience, a black dotted line is also displayed which indicates where $\hat {\omega }_\psi = \hat {\omega }_\alpha = 0$
. Additionally, the binormal and radial drifts are shown as dashed green and dash-dotted blue lines, respectively. For convenience, a black dotted line is also displayed which indicates where $\hat {\omega }_\psi = \hat {\omega }_\alpha = 0$![]() . It can be seen that energy is available over most of the magnetic well. Only the most shallowly trapped particles do not contribute to the Æ, as $\hat {\omega }_\alpha$
. It can be seen that energy is available over most of the magnetic well. Only the most shallowly trapped particles do not contribute to the Æ, as $\hat {\omega }_\alpha$![]() changes sign for these particles. This is in line with expectations, as the more deeply trapped particles experience ‘bad curvature’ only, which in turn drives the TEM unstable (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander Reference Helander2017). The contribution to the Æ from the trapped particle orbits is enhanced by the positive magnetic shear in DIII-D (Connor, Hastie & Martin Reference Connor, Hastie and Martin1983). The most shallowly trapped particles experience good curvature along most of their trajectories and exert, in contrast to the deeply trapped particles, a stabilizing influence. Note that this figure refers to a tokamak, which besides being exactly omnigenous only has a single trapping well. Stellarators generally have many different bounce wells, and non-omnigenous effects arise due to net radial drifts.
changes sign for these particles. This is in line with expectations, as the more deeply trapped particles experience ‘bad curvature’ only, which in turn drives the TEM unstable (Proll et al. Reference Proll, Helander, Connor and Plunk2012; Helander Reference Helander2017). The contribution to the Æ from the trapped particle orbits is enhanced by the positive magnetic shear in DIII-D (Connor, Hastie & Martin Reference Connor, Hastie and Martin1983). The most shallowly trapped particles experience good curvature along most of their trajectories and exert, in contrast to the deeply trapped particles, a stabilizing influence. Note that this figure refers to a tokamak, which besides being exactly omnigenous only has a single trapping well. Stellarators generally have many different bounce wells, and non-omnigenous effects arise due to net radial drifts.

Figure 3. The Æ per $\lambda$![]() for DIII-D. The flux tube is located at a normalized radial flux of $\psi /\psi _\mathrm {edge}=0.5$
for DIII-D. The flux tube is located at a normalized radial flux of $\psi /\psi _\mathrm {edge}=0.5$![]() .
.
To investigate how these circumstances change the distribution of Æ across different bounce wells, we show a plot of W7-X in its standard magnetic configuration in figure 4, with a density gradient of $L_\mathrm {ref}/L_n = 3$![]() . Several interesting features can be seen. The most pronounced difference to the previous figure is that the Æ is much more localized than in DIII-D, so that most of the contribution comes from a narrow range of bounce wells. Most of the Æ comes from bright bands in the central well, particularly those where the bounce well approaches the local maximum in $B$
. Several interesting features can be seen. The most pronounced difference to the previous figure is that the Æ is much more localized than in DIII-D, so that most of the contribution comes from a narrow range of bounce wells. Most of the Æ comes from bright bands in the central well, particularly those where the bounce well approaches the local maximum in $B$![]() around $\theta = 0$
around $\theta = 0$![]() . One can understand this observation in the following manner. Near the local maximum in field strength, the drift is maximally bad (as $\hat {\omega }_\alpha$
. One can understand this observation in the following manner. Near the local maximum in field strength, the drift is maximally bad (as $\hat {\omega }_\alpha$![]() is most negative), and the trapped particles in this region contribute significantly to the Æ. Furthermore, the Æ is weighted by $\hat {G}^{1/2}$
is most negative), and the trapped particles in this region contribute significantly to the Æ. Furthermore, the Æ is weighted by $\hat {G}^{1/2}$![]() , which is proportional to the bounce time, which becomes large near such a local maximum. These two effects combine in the central region, giving rise to the large Æ there. One can also see two bright bands at $B \approx 1.10$
, which is proportional to the bounce time, which becomes large near such a local maximum. These two effects combine in the central region, giving rise to the large Æ there. One can also see two bright bands at $B \approx 1.10$![]() , which at first seems puzzling as the particles experience on average good curvature in this band, as indicated by the positive sign of $\hat {\omega }_\alpha$
, which at first seems puzzling as the particles experience on average good curvature in this band, as indicated by the positive sign of $\hat {\omega }_\alpha$![]() . However, these particles experience a net radial drift ($\hat {\omega }_\psi \neq 0$
. However, these particles experience a net radial drift ($\hat {\omega }_\psi \neq 0$![]() ) and this non-omnigeneity causes the Æ to be non-zero. Furthermore, it is exacerbated by the large bounce time, resulting in the bright bands seen in the figure. Finally, one can see that, as in a tokamak, shallowly trapped particles barely contribute to the Æ, although the fraction of trapped particles which do not contribute is significantly larger than in DIII-D.
) and this non-omnigeneity causes the Æ to be non-zero. Furthermore, it is exacerbated by the large bounce time, resulting in the bright bands seen in the figure. Finally, one can see that, as in a tokamak, shallowly trapped particles barely contribute to the Æ, although the fraction of trapped particles which do not contribute is significantly larger than in DIII-D.

Figure 4. The Æ per $\lambda$![]() for W7-X (SC). The flux tube is located at a normalized radial flux of $\psi /\psi _\mathrm {edge}=0.5$
for W7-X (SC). The flux tube is located at a normalized radial flux of $\psi /\psi _\mathrm {edge}=0.5$![]() .
.
In summary, the distribution of Æ across various bounce wells indicates that it is the deeply trapped particles in regions of bad curvature which tend to be most destabilizing. Furthermore, the bounce time plays an important role in determining which particles contribute most to the Æ. Finally, we note that non-omnigenous effects can destabilize otherwise stable regions.
3.3 Dependence on gradient strength
We finally investigate how the Æ depends on the strength of the gradient $\hat {\omega }_*^T$![]() , when all other variables are kept constant. In the limit of large gradients, it is easy to see that (2.49) implies a linear scaling with the gradient strength. We go one step further and expand the integrand around large $\omega _*^T$
, when all other variables are kept constant. In the limit of large gradients, it is easy to see that (2.49) implies a linear scaling with the gradient strength. We go one step further and expand the integrand around large $\omega _*^T$![]() , which gives
, which gives
where $\mathrm {sgn}(x)=x/|x|$![]() is the sign function. In the opposite limit of small gradients, we find an important distinction between omnigenous and non-omnigenous devices. In a non-omnigenous device, one can expand (2.45) around small $\hat {\omega }_*^T$
is the sign function. In the opposite limit of small gradients, we find an important distinction between omnigenous and non-omnigenous devices. In a non-omnigenous device, one can expand (2.45) around small $\hat {\omega }_*^T$![]() , and one finds that in a weakly driven regime the integrand becomes
, and one finds that in a weakly driven regime the integrand becomes

For an exactly omnigenous device, however, this result vanishes due to the factor $\hat {\omega }_\psi ^2$![]() . To find the correct scaling for such devices, we return to the expression for the Æ of an omnigenous device first found in Helander (Reference Helander2020). Here, it was found that the Æ is proportional to
. To find the correct scaling for such devices, we return to the expression for the Æ of an omnigenous device first found in Helander (Reference Helander2020). Here, it was found that the Æ is proportional to
where $R[x] = (x + |x|)/2$![]() is the ramp function. Note that, when $\hat {\omega }_*^T$
is the ramp function. Note that, when $\hat {\omega }_*^T$![]() is small, the ramp function is non-zero in the region where $\omega _\alpha \rightarrow 0$
is small, the ramp function is non-zero in the region where $\omega _\alpha \rightarrow 0$![]() . If we assume there exists a point where $\omega _\alpha =0$
. If we assume there exists a point where $\omega _\alpha =0$![]() we can expand around the point $\hat {\omega }_\alpha (\lambda _0) = 0$
we can expand around the point $\hat {\omega }_\alpha (\lambda _0) = 0$![]() , and set
, and set
Next, we find the region where the argument of the ramp function is positive by finding where the argument vanishes
We can now perform the integral over the range $\lambda \in [\lambda _0,\lambda _0+ \hat {\omega }_*^T/\hat {\omega }_\lambda ]$![]() , and we find that the Æ to leading order is proportional to
, and we find that the Æ to leading order is proportional to

Thus we conclude that, for weakly driven omnigenous devices, the Æ integrand scales as
Hence, in summary, we have

The different scaling laws are displayed in figure 5, where we see a tokamak (which is exactly omnigenous), a non-omnigenous stellarator and the optimized, fairly omnigenous, HSX stellarator. The plots show a distinct ‘knee’ at the transition from one scaling law to the next. This knee is especially pronounced for the tokamak, and less so for the stellarator. The difference in scaling for weakly and strongly driven regimes is interesting, as the behaviour is reminiscent of gradient-threshold (also called critical-gradient) type behaviour. Such a gradient threshold is signified by small transport up to some threshold in the gradient followed by strong transport above this threshold (Dimits Reference Dimits2000), a behaviour shared by the present plot. It is thought that this critical gradient plays an important role in profile stiffness, where profiles tend to retain their shape without much sensitivity to the details of the particle/energy sources (Garbet et al. Reference Garbet, Mantica, Ryter, Cordey, Imbeaux, Sozzi, Manini, Asp, Parail and Wolf2004). It is also interesting to note that, from the different scaling laws for omnigenous and non-omnigenous devices, one would expect the critical-gradient-like behaviour of the Æ to be ‘softer’ in a non-omnigenous stellarator, as the transition from a quadratic to a linear scaling law is more gradual than that from a cubic one. If this gradient-threshold behaviour of the Æ indeed corresponds to the true critical gradient, this would result in profiles being less stiff, which has indeed observed in various stellarators (Milligen et al. Reference Milligen, Tribaldos, Vargas and Sanchez2008; Sanchez & Newman Reference Sanchez and Newman2015). Investigating HSX more closely, we see that for very low gradients it follows a quadratic scaling, for moderate gradients it approaches a third-power scaling and for strong gradient it is linear. This third-power region is a result of HSX being close to quasi-symmetry, so that $\hat {\omega }_\psi$![]() is small. However, at small enough gradients, the $\hat {\omega }_\psi$
is small. However, at small enough gradients, the $\hat {\omega }_\psi$![]() term starts to become important causing the scaling to be quadratic.
term starts to become important causing the scaling to be quadratic.

Figure 5. An example of the dependence of Æ on the gradient strength for three different devices; a tokamak, a non-omnigenous stellarator and HSX. In the case displayed above, the electron temperature gradient is set to zero. The dashed, dash-dotted, and dotted lines have a linear, square and third-power scaling with the density gradient, respectively.
Finally, we note the non-trivial dependence on $\hat {\omega }_\alpha$![]() in the various regimes. When the gradients are large, the Æ is linearly proportional to $\hat {\omega }_\alpha$
in the various regimes. When the gradients are large, the Æ is linearly proportional to $\hat {\omega }_\alpha$![]() , which quantifies ‘bad curvature’, but for small gradients it is inversely proportional to $\hat {\omega }_\alpha$
, which quantifies ‘bad curvature’, but for small gradients it is inversely proportional to $\hat {\omega }_\alpha$![]() . This implies that one can reduce the total Æ by increasing the amount of bad curvature. This would lead to reduced Æ in the weakly driven regime, and the ‘knee’ point would be shifted to higher $\hat {\omega }_*^T$
. This implies that one can reduce the total Æ by increasing the amount of bad curvature. This would lead to reduced Æ in the weakly driven regime, and the ‘knee’ point would be shifted to higher $\hat {\omega }_*^T$![]() , which would lead to a higher critical gradient (as estimated from Æ). This is in line with recent results of Roberg-Clark, Plunk & Xanthopoulos (Reference Roberg-Clark, Plunk and Xanthopoulos2022) and Roberg-Clark et al. (Reference Roberg-Clark, Plunk, Xanthopoulos, Nührenberg, Henneberg and Smith2023), who found that the critical gradient can be increased by introducing more bad curvature into the magnetic geometry, which thus leads to lower turbulent heat fluxes, although it should be noted that those results concern ion-temperature-gradient-driven transport. An important corollary of this property is that, in a device with particularly low Æ in the weakly driven regime (much bad curvature), the Æ becomes very large in the strongly driven regime, being linearly proportional to $\hat {\omega }_\alpha$
, which would lead to a higher critical gradient (as estimated from Æ). This is in line with recent results of Roberg-Clark, Plunk & Xanthopoulos (Reference Roberg-Clark, Plunk and Xanthopoulos2022) and Roberg-Clark et al. (Reference Roberg-Clark, Plunk, Xanthopoulos, Nührenberg, Henneberg and Smith2023), who found that the critical gradient can be increased by introducing more bad curvature into the magnetic geometry, which thus leads to lower turbulent heat fluxes, although it should be noted that those results concern ion-temperature-gradient-driven transport. An important corollary of this property is that, in a device with particularly low Æ in the weakly driven regime (much bad curvature), the Æ becomes very large in the strongly driven regime, being linearly proportional to $\hat {\omega }_\alpha$![]() when $\hat {\omega }_*^T \gg 1$
when $\hat {\omega }_*^T \gg 1$![]() . One can thus either have a device with a high gradient threshold and low Æ for small gradients (which may be attained by increasing the amount of bad curvature), or a device with low Æ in the strongly driven regime thanks to relatively little bad curvature in regions with many trapped particles.
. One can thus either have a device with a high gradient threshold and low Æ for small gradients (which may be attained by increasing the amount of bad curvature), or a device with low Æ in the strongly driven regime thanks to relatively little bad curvature in regions with many trapped particles.
4 Summary and conclusions
In this paper we have derived the Æ of trapped electrons in a slender flux tube of magnetically confined plasma, and we have compared it with nonlinear saturated radial electron energy fluxes as calculated by nonlinear gyrokinetic simulations. In deriving the Æ, several key insights were required to make progress. Firstly, it was found that the calculation is particularly simple in flux tubes with elliptical cross-section. An explicit expression of the ground state can then be found, which was used to calculate the Æ to leading order. The result is positive definite, as it must be, and reduces to a previously found expression in the case that the magnetic field is omnigenous. Since the Æ depends on the cross-section of the flux tube, its major and minor radii need to be chosen a priori. The correct choice depends on the correlation length of the turbulence, which we take to be proportional to the gyroradius in both directions.
We compared the resulting Æ for different magnetic geometries with the energy flux computed in a set of simulations of density-gradient-driven turbulence. The numerical Æ calculations are many orders of magnitude faster than the gyrokinetic simulations. The analysis is done for 4 different magnetic configurations, DIII-D, HSX and W7-X in its standard and high-mirror configurations. The saturated electron energy flux $Q_\textrm {sat}$![]() is approximately related to the Æ via a simple power law $Q_\textrm {sat} \propto A^{1.5 \pm 0.1}$
is approximately related to the Æ via a simple power law $Q_\textrm {sat} \propto A^{1.5 \pm 0.1}$![]() . A straightforward phenomenological model to explain the observed power law is proposed, which results in $Q_\textrm {sat} \propto A^{3/2}$
. A straightforward phenomenological model to explain the observed power law is proposed, which results in $Q_\textrm {sat} \propto A^{3/2}$![]() . We go on to investigate which regions are driving the available energy. The results can be understood in terms of simple geometrical concepts: bad curvature (resulting in the drift being in resonance with the drift wave) and non-omnigeneity drive Æ. We finally investigate the dependence of Æ on gradient and find that there are three distinct scaling laws; for strong gradients the Æ scales linearly with the gradient strength, whereas for weak gradients the Æ scales as the gradient strength squared or cubed for non-omnigenous or exactly omnigenous fields, respectively.
. We go on to investigate which regions are driving the available energy. The results can be understood in terms of simple geometrical concepts: bad curvature (resulting in the drift being in resonance with the drift wave) and non-omnigeneity drive Æ. We finally investigate the dependence of Æ on gradient and find that there are three distinct scaling laws; for strong gradients the Æ scales linearly with the gradient strength, whereas for weak gradients the Æ scales as the gradient strength squared or cubed for non-omnigenous or exactly omnigenous fields, respectively.
These results are interesting for future research. The strong correlation between Æ and energy flux across various devices indicates that it may serve as a good proxy function for stellarator optimization codes (Spong et al. Reference Spong, Hirshman, Berry, Lyon, Fowler, Strickler, Cole, Nelson, Williamson and Ware2001; Landreman et al. Reference Landreman, Medasani, Wechsung, Giuliani, Jorge and Zhu2021) used to design stellarators with reduced turbulence. Direct gyrokinetic simulations can be too time consuming to be carried out inside the optimization loop in such codes, so there is a need for more efficiently estimating turbulent transport in given magnetic field. It is thus of interest to understand how Æ is related to specific details in the field-line geometry. As we have seen, regions of bad curvature are associated with large Æ, thus providing a connection between previously known results from linear gyrokinetic stability theory and Æ, but the latter also seems to possess predictive qualities for nonlinear transport. Furthermore, one could also use the Æ derived here as a profile optimization tool for TEM-dominated devices. One could then search for plasma profiles and adjustable coil currents which minimize the Æ, under some set of constraints. Finally, it may also be valuable to derive expressions for Æ in more generic scenarios where turbulence is driven by an ion temperature gradient.
Acknowledgements
The authors are grateful for the valuable discussions with, J.M. Duff, J. Ball, T. Görler, M.J. Pueschel, P. Mulholland, P. Costello, M.J. Gerard and E. Rodriguez. This work was partly supported by a grant from the Simons Foundation (560651, PH), and this publication is part of the project ‘Shaping turbulence – building a framework for turbulence optimization of fusion reactors’, with Project No. OCENW.KLEIN.013 of the research program ‘NWO Open Competition Domain Science’ which is financed by the Dutch Research Council (NWO). This work has been carried out within the framework of the EUROfusion Consortium, funded by the European Union via the Euratom Research and Training Program (Grant Agreement No. 101052200 – EUROfusion). Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Commission. Neither the European Union nor the European Commission can be held responsible for them.
Editor Tünde Fülöp thanks the referees for their advice in evaluating this article.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Details of the derivation of the domain shape
Here, we provide mathematical details for the argument given in § 2 concerning the domain shape. We do so by means of a geometric argument, sketched in figure 6. Here, $\mathrm {A}$![]() and $\mathrm {A}'$
and $\mathrm {A}'$![]() denote two points on the boundary with parallel tangents, $T_{\mathrm {A}}$
denote two points on the boundary with parallel tangents, $T_{\mathrm {A}}$![]() and $T_{\mathrm {{A}'}}$
and $T_{\mathrm {{A}'}}$![]() , respectively. The distance between these tangents is $2D$
, respectively. The distance between these tangents is $2D$![]() and the radius of curvature of the boundary at $\mathrm {A}$
and the radius of curvature of the boundary at $\mathrm {A}$![]() is $R$
is $R$![]() . If $\mathrm {C}$
. If $\mathrm {C}$![]() is the point on $T_{\mathrm {A}'}$
is the point on $T_{\mathrm {A}'}$![]() that is closest to $\mathrm {A}$
that is closest to $\mathrm {A}$![]() we thus have $|\mathrm {AC}|=2D$
we thus have $|\mathrm {AC}|=2D$![]() . Next, we let $\mathrm {B}$
. Next, we let $\mathrm {B}$![]() and $\mathrm {B}'$
and $\mathrm {B}'$![]() denote boundary points in the vicinity $\mathrm {A}$
denote boundary points in the vicinity $\mathrm {A}$![]() and $\mathrm {A}'$
and $\mathrm {A}'$![]() , respectively, such that the tangents through $\mathrm {B}$
, respectively, such that the tangents through $\mathrm {B}$![]() and $\mathrm {B}'$
and $\mathrm {B}'$![]() are parallel, and we denote by $\mathrm {E}$
are parallel, and we denote by $\mathrm {E}$![]() the point on the tangent through $\mathrm {B}'$
the point on the tangent through $\mathrm {B}'$![]() that is closest to $\mathrm {B}$
that is closest to $\mathrm {B}$![]() . Let us write the distance $|\mathrm {BE}|=2(D+\mathrm {d}D)$
. Let us write the distance $|\mathrm {BE}|=2(D+\mathrm {d}D)$![]() and define $|\mathrm {A}'\mathrm {C}|=2L$
and define $|\mathrm {A}'\mathrm {C}|=2L$![]() . To leading order in smallness of $\mathrm {d} \vartheta$
. To leading order in smallness of $\mathrm {d} \vartheta$![]() we have $|\mathrm {DC}|=2D \mathrm {d} \vartheta$
we have $|\mathrm {DC}|=2D \mathrm {d} \vartheta$![]() . Furthermore, to leading order $|\mathrm {B}'\mathrm {E}|=2L$
. Furthermore, to leading order $|\mathrm {B}'\mathrm {E}|=2L$![]() , implying that $|\mathrm {FE}|=2L\mathrm {d}\vartheta$
, implying that $|\mathrm {FE}|=2L\mathrm {d}\vartheta$![]() , where $\mathrm {F}$
, where $\mathrm {F}$![]() denotes the intersection of $\mathrm {BE}$
denotes the intersection of $\mathrm {BE}$![]() and $\mathrm {A}'\mathrm {C}$
and $\mathrm {A}'\mathrm {C}$![]() . All in all we find the leading-order relations
. All in all we find the leading-order relations


Figure 6. A geometric sketch showing the relation between $D$![]() and $R$
and $R$![]() . The green vertical lines passing through $A$
. The green vertical lines passing through $A$![]() and $A'$
and $A'$![]() are tangent to the boundary, as are the red ones passing through $B$
are tangent to the boundary, as are the red ones passing through $B$![]() and $B'$
and $B'$![]() .
.
Next, we investigate how $L$![]() changes under some small change $\mathrm {d}\vartheta$
changes under some small change $\mathrm {d}\vartheta$![]() . Let us define $|\mathrm {B}'\mathrm {E}|=2L' = 2(L+ \mathrm {d}L)$
. Let us define $|\mathrm {B}'\mathrm {E}|=2L' = 2(L+ \mathrm {d}L)$![]() . Since $|\mathrm {AB}|=|\mathrm {A}'\mathrm {B}'|=R\mathrm {d}\vartheta$
. Since $|\mathrm {AB}|=|\mathrm {A}'\mathrm {B}'|=R\mathrm {d}\vartheta$![]() and $|\mathrm {CD}|=2D\mathrm {d}\vartheta$
and $|\mathrm {CD}|=2D\mathrm {d}\vartheta$![]() , we have
, we have

Combining these relations, one finds
and since $R = C_\mathcal {A}/D^3$![]() the equation for the domain can be written as
the equation for the domain can be written as
It is straightforward to solve for the inverse function, $\vartheta (D)$![]() , which becomes
, which becomes

where the integration constant constitutes an unimportant phase, which we can chose conveniently, e.g.
The radius of curvature thus becomes
Our final step is to verify that an ellipse has similar curvature. We first realize that
which for an ellipse, $x^2/a^2 + y^2/b^2 = 1$![]() implies that
implies that
Now, the radius of curvature for an ellipse may be written as

This is of the same form as (A7), showing us that the ellipse is indeed the only sufficiently smooth solution to the problem.
Appendix B. Relating derivatives to bounce-averaged frequencies
Here, we show how the derivatives of the energy and distribution function can be related to bounce averaged frequencies. By investigating the bounce-averaged Lagrangian of charged particles in electromagnetic fields, one can derive the following relations (Helander & Sigmar Reference Helander and Sigmar2005; Helander Reference Helander2014):
Here, $\delta \psi$![]() is the total excursion in the $\psi$
is the total excursion in the $\psi$![]() direction after a full bounce motion, $\delta \alpha$
direction after a full bounce motion, $\delta \alpha$![]() is the total excursion in the $\alpha$
is the total excursion in the $\alpha$![]() direction after a full bounce motion and $\tau _b$
direction after a full bounce motion and $\tau _b$![]() is the bounce time. In general, we know that the second adiabatic invariant can be written as
is the bounce time. In general, we know that the second adiabatic invariant can be written as
Taking the total differential of $\mathcal {J}$![]() we thus find
we thus find
This allows us to readily find the derivatives of the energy function. We conclude that
With these findings the derivatives of the Maxwellian can readily be evaluated
Here, we have defined the electron diamagnetic drift frequency as $\omega _*^T$![]() as
as
and we have denoted the ratio between the gradients as $\eta = (\mathrm {d} \ln {T} / \mathrm {d} \psi ) / (\mathrm {d} \ln {n} / \mathrm {d} \psi )$![]() .
.