Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T17:27:47.205Z Has data issue: false hasContentIssue false
  • English
  • Français

Alternative representation of the dielectric tensor for a relativistic magnetized plasma in thermal equilibrium

Published online by Cambridge University Press:  13 March 2009

Peter H. Yoon  and
Ronald C. Davidson
Peter H. Yoon
Affiliation:
Institute for Physical Science and Technology, University of Maryland, College Park, Maryland 20742, U.S.A.
Ronald C. Davidson
Affiliation:
Plasma Fusion Center, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Abstract

An alternative representation of the dielectric tensor εij(k, ω) for a relativistic magnetized plasma in thermal equilibrium is presented. This representation involves an infinite series expansion in powers of 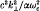, as well as an asymptotic expansion for large 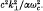Here ωc = eB0/mc is the nonrelativistic cyclotron frequency, k⊥ is the wavenumber perpendicular to the magnetic field B0êz, and α is the dimensionless parameter defined by α = mc2/KBT. The present work generalizes Shkarofsky's (1966) representation. Moreover, unlike Trubnikov's (1958) formal result, in which the k⊥ and kz dependences of εij(k, ω) are inexorably coupled, the present representation naturally separates the k⊥ and kz dependences of εij(k, ω). As an application, the general expression is simplified for the case of a weakly relativistic plasma, and the dispersion relation is obtained for electromagnetic waves, including first-order relativistic effects. The method developed in this paper can be used for other non-thermal distributions.

Type
Research Article
Information
Journal of Plasma Physics , Volume 43 , Issue 2 , April 1990 , pp. 269 - 281
Copyright
Copyright © Cambridge University Press 1990

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Airoldi, A. C. & Orefice, A. 1982 J. Plasma Phys. 27, 515.CrossRefGoogle Scholar
Bornatici, M., Cano, R., De Barbieri, O. & Engelmann, F. 1983 Nucl. Fusion, 23, 1153.CrossRefGoogle Scholar
Davidson, R. C. 1983 Handbook of Plasma Physics, vol. 1, p. 521. North-Holland.Google Scholar
Davidson, R. C. & Yoon, P. H. 1989 Phys. Fluids B, 1, 195.CrossRefGoogle Scholar
Dnestrovskii, Yu. N., Kostomarov, D. R. & Skrydlov, N. U. 1964 Soviet Phys. Tech. Phys. 8, 691.Google Scholar
Imre, K. 1962 Phys. Fluids, 5, 459.CrossRefGoogle Scholar
Lee, L. C. & Wu, C. S. 1980 Phys. Fluids, 23, 1348.CrossRefGoogle Scholar
Pritchett, P. L. 1984 J. Geophys. Res. 89, 8957.CrossRefGoogle Scholar
Robinson, P. A. 1986 J. Math. Phys. 27, 1206.CrossRefGoogle Scholar
Shkarofsky, I. P. 1966 Phys. Fluids, 9, 561.CrossRefGoogle Scholar
Shkarofsky, I. P. 1986 J. Plasma Phys. 35, 319.CrossRefGoogle Scholar
Trubnikov, B. A. 1958 Plasma Physics and the Problem of Controlled Thermonuclear Reactions, p. 122. Pergamon.Google Scholar
Wong, H. K., Wu, C. S. & Gaffey, J. D. 1985 Phys. Fluids, 28, 2751.CrossRefGoogle Scholar
Yoon, P. H. 1990 Phys. Fluids, B 2, in press.Google Scholar