Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T15:42:31.742Z Has data issue: false hasContentIssue false
  • English
  • Français

Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. Part 2. Applications

Part of: Focus on Fusion

Published online by Cambridge University Press:  13 January 2020

Elizabeth J. Paul Open the ORCID record for Elizabeth J. Paul [Opens in a new window] ,
Thomas Antonsen Jr ,
Matt Landreman Open the ORCID record for Matt Landreman [Opens in a new window]  and
W. Anthony Cooper
Elizabeth J. Paul*
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park,MD 20740, USA
Thomas Antonsen Jr
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park,MD 20740, USA
Matt Landreman
Affiliation:
Institute for Research in Electronics and Applied Physics, University of Maryland, College Park,MD 20740, USA
W. Anthony Cooper
Affiliation:
Swiss Alps Fusion Energy (SAFE), CH-1864 Vers l’Eglise, Switzerland
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The shape gradient is a local sensitivity function defined on the surface of an object which provides the change in a characteristic quantity, or figure of merit, associated with a perturbation to the shape of the object. The shape gradient can be used for gradient-based optimization, sensitivity analysis and tolerance calculations. However, it is generally expensive to compute from finite-difference derivatives for shapes that are described by many parameters, as is the case for typical stellarator geometry. In an accompanying work (Antonsen, Paul & Landreman J. Plasma Phys., vol. 85 (2), 2019), generalized self-adjointness relations are obtained for magnetohydrodynamic (MHD) equilibria. These describe the relation between perturbed equilibria due to changes in the rotational transform or toroidal current profiles, displacements of the plasma boundary, modifications of currents in the vacuum region or the addition of bulk forces. These are applied to efficiently compute the shape gradient of functions of MHD equilibria with an adjoint approach. In this way, the shape derivative with respect to any perturbation applied to the plasma boundary or coil shapes can be computed with only one additional MHD equilibrium solution. We demonstrate that this approach is applicable for several figures of merit of interest for stellarator configuration optimization: the magnetic well, the magnetic ripple on axis, the departure from quasisymmetry, the effective ripple in the low-collisionality 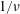$1/\unicode[STIX]{x1D708}$ regime 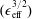$(\unicode[STIX]{x1D716}_{\text{eff}}^{3/2})$ (Nemov et al. Phys. Plasmas, vol. 6 (12), 1999, pp. 4622–4632) and several finite-collisionality neoclassical quantities. Numerical verification of this method is demonstrated for the magnetic well figure of merit with the VMEC code (Hirshman & Whitson Phys. Fluids, vol. 26 (12), 1983, p. 3553) and for the magnetic ripple with modification of the ANIMEC code (Cooper et al. Comput. Phys. Commun., vol. 72 (1), 1992, pp. 1–13). Comparisons with the direct approach demonstrate that, in order to obtain agreement within several per cent, the adjoint approach provides a factor of 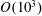$O(10^{3})$ in computational savings.

Keywords

fusion plasmaplasma simulation
Type
Research Article
Information
Journal of Plasma Physics , Volume 86 , Issue 1 , February 2020 , 905860103
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, D. V., Cooper, W. A., Gruber, R., Merazzi, S. & Schwenn, U. 1990 Methods for the efficient calculation of the (MHD) magnetohydrodynamic stability properties of magnetically confined fusion plasmas. Intl J. Supercomput. Appl. 4 (3), 34–47.CrossRefGoogle Scholar
Antonsen, T. M. & Lee, Y. C. 1982 Electrostatic modification of variational principles for anisotropic plasmas. Phys. Fluids 25 (1), 132–142.CrossRefGoogle Scholar
Antonsen, T. M., Paul, E. J. & Landreman, M. 2019 Adjoint approach to calculating shape gradients for three-dimensional magnetic confinement equilibria. J. Plasma Phys. 85 (2), 905850207.CrossRefGoogle Scholar
Bernstein, I. B., Frieman, E. A., Kruskal, M. D. & Kulsrud, R. M. 1958 An energy principle for hydromagnetic stability problems. Proc. R. Soc. Lond. A 244 (1236), 17.Google Scholar
Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24 (11), 1999–2003.CrossRefGoogle Scholar
Boozer, A. H. 1995 Quasi-helical symmetry in stellarators. Plasma Phys. Control. Fusion 37 (11A), A103.CrossRefGoogle Scholar
Boozer, A. H. & Nührenberg, C. 2006 Perturbed plasma equilibria. Phys. Plasmas 13 (10), 102501.CrossRefGoogle Scholar
Carreras, B. A., Lynch, V. E. & Ware, A.1996 Configuration studies for a small-aspect-ratio tokamak stellarator hybrid. Tech. Rep. Oak Ridge National Lab.CrossRefGoogle Scholar
Connor, J. W. & Hastie, R. J. 1974 Neoclassical diffusion in an $l=3$ stellarator. Phys. Fluids 17 (114), 114–123.CrossRefGoogle Scholar
Cooper, W. A., Graves, J. P., Hirshman, S. P., Yamaguchi, T., Narushima, Y., Okamura, S., Sakakibara, S., Suzuki, C., Watanabe, K. Y., Yamada, H. et al. 2006 Anisotropic pressure bi-Maxwellian distribution function model for three-dimensional equilibria. Nucl. Fusion 46 (7), 683.CrossRefGoogle Scholar
Cooper, W. A., Hirshman, S. P., Merazzi, S. & Gruber, R. 1992 3D magnetohydrodynamic equilibria with anisotropic pressure. Comput. Phys. Commun. 72 (1), 1–13.CrossRefGoogle Scholar
Cooper, W. A., Hirshman, S. P., Yamaguchi, T., Narushima, Y., Okamura, S., Sakakibara, S., Suzuki, C., Watanabe, K. Y., Yamada, H. & Yamazaki, K. 2005 Three-dimensional anisotropic pressure equilibria that model balanced tangential neutral beam injection effects. Plasma Phys. Control. Fusion 47 (3), 561.CrossRefGoogle Scholar
Delfour, M. C. & Zolésio, J.-P. 2011a Shapes and geometries: metrics, analysis, differential calculus, and optimization. In Advances in Design and Control, vol. 22, chap. 4, SIAM.Google Scholar
Delfour, M. C. & Zolésio, J.-P. 2011b Shapes and geometries: metrics, analysis, differential calculus, and optimization. In Advances in Design and Control, vol. 22, chap. 9, SIAM.Google Scholar
Drevlak, M. C., Beidler, C. D., Geiger, J., Helander, P. & Turkin, Y. 2018 Optimisation of stellarator equilibria with ROSE. Nucl. Fusion 59 (1), 016010.Google Scholar
Drevlak, M. C., Brochard, F., Helander, P., Kisslinger, J., Mikhailov, M., Nührenberg, C., Nührenberg, J. & Turkin, Y. 2013 ESTELL: a quasi-toroidally symmetric stellarator. Contrib. Plasma Phys. 53 (6), 459–468.CrossRefGoogle Scholar
Drevlak, M. C., Geiger, J., Helander, P. & Turkin, Y. 2014 Fast particle confinement with optimized coil currents in the W7-X stellarator. Nucl. Fusion 54 (7), 073002.CrossRefGoogle Scholar
Freidberg, J. P. 2014 Ideal MHD. chap. 12. Cambridge University Press.CrossRefGoogle Scholar
Frieman, E. A. 1970 Collisional diffusion in nonaxisymmetric toroidal systems. Phys. Fluids 13 (490), 490–496.CrossRefGoogle Scholar
Galeev, A. A. & Sagdeev, R. Z. 1979 Theory of neoclassical diffusion. In Reviews of Plasma Physics, vol. 7, p. 257. Springer.Google Scholar
Gardner, H. 1990 Modelling the behaviour of the magnetic field diagnostic coils on the W VII-AS stellarator using a three-dimensional equilibrium code. Nucl. Fusion 30 (8), 1417.CrossRefGoogle Scholar
Helander, P. 2014 Theory of plasma confinement in non-axisymmetric magnetic fields. Rep. Prog. Phys. 77 (8), 087001.CrossRefGoogle ScholarPubMed
Henneberg, S. A., Drevlak, M., Nührenberg, C., Beidler, C. D., Turkin, Y., Loizu, J. & Helander, P. 2019 Properties of a new quasi-axisymmetric configuration. Nucl. Fusion 59 (2), 026014.CrossRefGoogle Scholar
Hirshman, S. P., Spong, D. A., Whitson, J. C., Nelson, B., Batchelor, D. B., Lyon, J. F., Sanchez, R., Brooks, A., Y.-Fu, G., Goldston, R. J. et al. 1999 Physics of compact stellarators. Phys. Plasmas 6 (5), 1858–1864.CrossRefGoogle Scholar
Hirshman, S. P. & Whitson, J. C. 1983 Steepest descent moment method for three-dimensional magnetohydrodynamic equilibria. Phys. Fluids 26 (12), 3553.CrossRefGoogle Scholar
Ho, D.-M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30 (2), 442–461.CrossRefGoogle Scholar
Hudson, S. R., Zhu, C., Pfefferlé, D. & Gunderson, L. 2018 Differentiating the shape of stellarator coils with respect to the plasma boundary. Phys. Lett. A 382 (38), 2732–2737.CrossRefGoogle Scholar
Ku, L. P., Garabedian, P. R., Lyon, J., Turnbull, A., Grossman, A., Mau, T. K., Zarnstorff, M. & ARIES Team 2008 Physics design for ARIES-CS. Fusion Sci. Technol. 54 (3), 673–693.CrossRefGoogle Scholar
Landreman, M. & Paul, E. J. 2018 Computing local sensitivity and tolerances for stellarator physics properties using shape gradients. Nucl. Fusion 58 (7), 076023.CrossRefGoogle Scholar
Landreman, M., Smith, H. M., Mollén, A. & Helander, P. 2014 Comparison of particle trajectories and collision operators for collisional transport in nonaxisymmetric plasmas. Phys. Plasmas 21 (4), 042503.CrossRefGoogle Scholar
Lazerson, S. A. 2012 The virtual-casing principle for 3D toroidal systems. Plasma Phys. Control. Fusion 54 (12), 122002.CrossRefGoogle Scholar
Liu, H., Shimizu, A., Isobe, M., Okamura, S., Nishimura, S., Suzuki, C., Xu, Y., Zhang, X., Liu, B., Huang, J. et al. 2018 Magnetic configuration and modular coil design for the Chinese First Quasi-Axisymmetric Stellarator. Plasma Fusion Res. 13, 3405067.CrossRefGoogle Scholar
Mercier, C. & Luc, H.1974 The MHD approach to the problem of plasma confinement in closed magnetic configurations. Lectures in Plasma Physics. (Commission of the European Communities).Google Scholar
Nemov, V. V., Kasilov, S. V., Kernbichler, W. & Heyn, M. F. 1999 Evaluation of $1/\unicode[STIX]{x1D708}$ neoclassical transport in stellarators. Phys. Plasmas 6 (12), 4622–4632.CrossRefGoogle Scholar
Nemov, V. V., Kasilov, S. V., Kernbichler, W. & Leitold, G. O. 2005 The $\unicode[STIX]{x1D735}B$ drift velocity of trapped particles in stellarators. Phys. Plasmas 12 (11), 112507.CrossRefGoogle Scholar
Nührenberg, C. & Boozer, A. H. 2003 Magnetic islands and perturbed plasma equilibria. Phys. Plasmas 10 (7), 2840–2851.CrossRefGoogle Scholar
Nührenberg, J. & Zille, R. 1988 Quasi-helically symmetric toroidal stellarators. Phys. Lett. A 129, 113–117.CrossRefGoogle Scholar
Paul, E. J., Abel, I. G., Landreman, M. & Dorland, W. 2019 An adjoint method for neoclassical stellarator optimization. J. Plasma Phys. 85 (5), 795850501.CrossRefGoogle Scholar
Proll, J. H. E., Mynick, H. E., Xanthopoulos, P., Lazerson, S. A. & Faber, B. J. 2015 TEM turbulence optimisation in stellarators. Plasma Phys. Control. Fusion 58 (1), 014006.Google Scholar
Reiman, A., Fu, G., Hirshman, S., Ku, L., Monticello, D., Mynick, H., Redi, M., Spong, D., Zarnstorff, M., Blackwell, B. et al. 1999 Physics design of a high-quasi-axisymmetric stellarator. Plasma Phys. Control. Fusion 41 (12B), B273.CrossRefGoogle Scholar
Rudin, W. 2006 Real and Complex Analysis. chap. 4, Tata McGraw-Hill Education.Google Scholar
Schwab, C. 1993 Ideal magnetohydrodynamics: Global mode analysis of three-dimensional plasma configurations. Phys. Fluids B 5 (9), 3195–3206.CrossRefGoogle Scholar
Shimizu, A., Liu, H., Isobe, M., Okamura, S., Nishimura, S., Suzuki, C., Xu, Y., Zhang, X., Liu, B., Huang, J. et al. 2018 Configuration property of the Chinese First Quasi-Axisymmetric Stellarator. Plasma Fusion Res. 13, 3403123.CrossRefGoogle Scholar
Spong, D. A., Hirshman, S. P., Berry, L. A., Lyon, J. F., Fowler, R. H., Strickler, D. J., Cole, M. J., Nelson, B. N., Williamson, D. E., Ware, A. S. et al. 2001 Physics issues of compact drift optimized stellarators. Nucl. Fusion 41 (6), 711.CrossRefGoogle Scholar
Strickler, D. J., Hirshman, S. P., Spong, D. A., Cole, M. J., Lyon, J. F., Nelson, B. E., Williamson, D. E. & Ware, A. S. 2004 Development of a robust quasi-poloidal compact stellarator. Fusion Sci. Technol. 45 (1), 15–26.CrossRefGoogle Scholar
Strumberger, E. & Günter, S. 2016 CASTOR3D: linear stability studies for 2D and 3D tokamak equilibria. Nucl. Fusion 57 (1), 016032.Google Scholar
Williamson, D., Brooks, A., Brown, T., Chrzanowski, J., Cole, M., Fan, H., Freudenberg, K., Fogarty, P., Hargrove, T., Heitzenroeder, P. et al. 2005 Challenges in designing the modular coils for the National Compact Stellarator Experiment (NCSX). In Fusion Engineering 2005, Twenty-First IEEE/NPS Symposium on, p. 1. IEEE.Google Scholar
Zarnstorff, M. C., Berry, L. A., Brooks, A., Fredrickson, E., Fu, G.-Y., Hirshman, S., Hudson, S., Ku, L.-P., Lazarus, E., Mikkelsen, D. et al. 2001 Physics of the compact advanced stellarator NCSX. Plasma Phys. Control. Fusion 43 (12A), A237.CrossRefGoogle Scholar