Hostname: page-component-cc8bf7c57-n7qbj Total loading time: 0 Render date: 2024-12-12T01:58:19.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of the shock velocity determined from the magnetohydrodynamic jump conditions

Part of: Focus on Plasma Astrophysics Space Weather Special Issue Present Achievements in SpacePlasmas

Published online by Cambridge University Press:  19 December 2018

John J. Podesta
John J. Podesta*
Affiliation:
Center for Space Plasma Physics, Space Science Institute, Boulder, CO 80301, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Spacecraft measurements of propagating interplanetary shocks are often interpreted using the ideal magnetohydrodynamic (MHD) model of a planar shock wave travelling with constant velocity 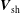$\boldsymbol{V}_{\text{sh}}$ through a spatially uniform plasma. In particular, measurements of the plasma variables upstream and downstream have long been used in conjunction with the Rankine–Hugoniot conditions, also known as the MHD jump conditions, to determine shock velocities and other physical parameters of interplanetary shocks. This procedure is justified only if the shock velocity determined by the MHD jump conditions is unique. In this study the important property of uniqueness is demonstrated for non-perpendicular shocks in MHD media characterized by an isotropic pressure tensor. The primary conclusion is that the shock velocity is uniquely determined by the jump conditions regardless of the type of shock (slow, intermediate or fast). Several new formulas for the shock speed are also derived including one that is independent of the shock normal 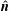$\hat{\boldsymbol{n}}$. In principle, the solution technique developed here can be applied to estimate 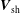$\boldsymbol{V}_{\text{sh}}$ using solar wind data provided the measurements obey the MHD shock model with sufficient accuracy. That is not its intended purpose, however, and such applications are beyond the scope of this work.

Keywords

astrophysical plasmasspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 84 , Issue 6 , December 2018 , 765840601
Copyright
© Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham-Shrauner, B. 1972 Determination of magnetohydrodynamic shock normals. J. Geophys. Res. 77, 736–739.Google Scholar
Abraham-Shrauner, B. & Yun, S. H. 1976 Interplanetary shocks seen by AMES plasma probe on Pioneer 6 and 7. J. Geophys. Res. 81, 2097–2102.Google Scholar
Balogh, A. & Riley, P. 1997 Overview of heliospheric shocks. In Cosmic Winds and the Heliosphere (ed. Jokipii, J. R., Sonett, C. P. & Giampapa, M. S.), pp. 359–387. University of Arizona Press.Google Scholar
Berdichevsky, D. B., Szabo, A., Lepping, R. P., Viñas, A. F. & Mariani, F. 2000 Interplanetary fast shocks and associated drivers observed through the 23rd solar minimum by Wind over its first 2.5 years. J. Geophys. Res. 105, 27289–27314.Google Scholar
Chao, J. K.1970 Interplanetary collisionless shock waves. PhD thesis, Massachusetts Institute of Technology.Google Scholar
Colburn, D. S. & Sonett, C. P. 1966 Discontinuities in the solar wind. Space Sci. Rev. 5, 439–506.Google Scholar
Hsieh, K. C. & Richter, A. K. 1986 The importance of being earnest about shock fitting. J. Geophys. Res. 91, 4157–4162.Google Scholar
Hudson, P. D. 1970 Discontinuities in an anisotropic plasma and their identification in the solar wind. Planet. Space Sci. 18, 1611–1622.Google Scholar
Landau, L. D. & Lifshitz, E. M. 1960 Electrodynamics of Continuous Media. Pergamon Press.Google Scholar
Lepping, R. P. & Argentiero, P. D. 1971 Single spacecraft method of estimating shock normals. J. Geophys. Res. 76, 4349–4359.Google Scholar
Ogilvie, K. W. & Burlaga, L. F. 1969 Hydromagnetic shocks in the solar wind. Solar Phys. 8, 422–434.Google Scholar
Oh, S. Y., Yi, Y. & Kim, Y. H. 2007 Solar cycle variation of the interplanetary forward shock drivers observed at 1 AU. Solar Phys. 245, 391–410.Google Scholar
Russell, C. T., Mellott, M. M., Smith, E. J. & King, J. H. 1983 Multiple spacecraft observations of interplanetary shocks: four spacecraft determination of shock normals. J. Geophys. Res. 88, 4739–4748.Google Scholar
Sonett, C. P., Colburn, D. S., Davis, L., Smith, E. J. & Coleman, P. J. 1964 Evidence for a collision-free magnetohydrodynamic shock in interplanetary space. Phys. Rev. Lett. 13, 153–156.Google Scholar
Szabo, A. 1994 An improved solution to the ‘Rankine–Hugoniot’ problem. J. Geophys. Res. 99, 14737–14746.Google Scholar
Viñas, A. F. & Scudder, J. D. 1986 Fast and optimal solution to the ‘Rankine–Hugoniot problem’. J. Geophys. Res. 91, 39–58.Google Scholar
Volkmer, P. M. & Neubauer, F. M. 1985 Statistical properties of fast magnetoacoustic shock waves in the solar wind between 0.3 AU and 1 AU – Helios-1, 2 observations. Ann. Geophys. 3, 1–12.Google Scholar