Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-18T04:58:18.938Z Has data issue: false hasContentIssue false
  • English
  • Français

Stochastic layer scaling in the two-wire model for divertor tokamaks

Published online by Cambridge University Press:  01 June 2009

HALIMA ALI ,
ALKESH PUNJABI  and
ALLEN BOOZER
HALIMA ALI
Affiliation:
Hampton University, Hampton, VA 23668, USA ([email protected])
ALKESH PUNJABI
Affiliation:
Hampton University, Hampton, VA 23668, USA ([email protected])
ALLEN BOOZER
Affiliation:
Columbia University, New York, NY 10027, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

The question of magnetic field structure in the vicinity of the separatrix in divertor tokamaks is studied. The authors have investigated this problem earlier in a series of papers, using various mathematical techniques. In the present paper, the two-wire model (TWM) [Reiman, A. 1996 Phys. Plasmas3, 906] is considered. It is noted that, in the TWM, it is useful to consider an extra equation expressing magnetic flux conservation. This equation does not add any more information to the TWM, since the equation is derived from the TWM. This equation is useful for controlling the step size in the numerical integration of the TWM equations. The TWM with the extra equation is called the flux-preserving TWM. Nevertheless, the technique is apparently still plagued by numerical inaccuracies when the perturbation level is low, resulting in an incorrect scaling of the stochastic layer width. The stochastic broadening of the separatrix in the flux-preserving TWM is compared with that in the low mn (poloidal mode number m and toroidal mode number n) map (LMN) [Ali, H., Punjabi, A., Boozer, A. and Evans, T. 2004 Phys. Plasmas11, 1908]. The flux-preserving TWM and LMN both give Boozer–Rechester 0.5 power scaling of the stochastic layer width with the amplitude of magnetic perturbation when the perturbation is sufficiently large [Boozer, A. and Rechester, A. 1978, Phys. Fluids21, 682]. The flux-preserving TWM gives a larger stochastic layer width when the perturbation is low, while the LMN gives correct scaling in the low perturbation region. Area-preserving maps such as the LMN respect the Hamiltonian structure of field line trajectories, and have the added advantage of computational efficiency. Also, for a 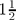degree of freedom Hamiltonian system such as field lines, maps do not give Arnold diffusion.

Type
Papers
Information
Journal of Plasma Physics , Volume 75 , Issue 3 , June 2009 , pp. 303 - 318
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Cordey, J. D., Goldston, R. J. and Parker, R. R. 1992 Phys. Today 45 (1), 22.Google Scholar
[2]Boozer, A. and Rechester, A. 1978 Phys. Fluids 21, 682.Google Scholar
[3]Luxon, J. L. and Davis, L. E. 1985 Fusion Technol. 8, 441.CrossRefGoogle Scholar
[4]Evans, T. E. et al. 2006 Nature Phys. 2, 419.CrossRefGoogle Scholar
[5]Boozer, A. 1983 Phys. Fluids 26, 1288.Google Scholar
[6]Cary, J. R. and Littlejohn, R. G. 1983 Ann. Phys. (N.Y.) 151, 1.Google Scholar
[7]Post, D. E. et al. 1991 ITER Documentation Series No. 21. Vienna: IAEA.Google Scholar
[8]Reiman, A. 1996 Phys. Plasmas 3, 906.CrossRefGoogle Scholar
[9]Lau, Y. and Finn, J. 1991 Astrophys. J. 366, 577.CrossRefGoogle Scholar
[10]Stern, D. P. 1973 J. Geophys. Res. 78, 7292.Google Scholar
[11]Greene, J. M. 1988 J. Geophys. Res. A 93, 8583.CrossRefGoogle Scholar
[12]Snipes, J. A., Campbell, D. J., Hender, T. C., Hellermann, M. V. and Weisen, H. 1990 Nucl. Fusion 30, 205.CrossRefGoogle Scholar
[13]Zohm, H., Kallenbach, A., Bruhns, H., Fussmann, G. and Klueber, O. 1990 Europhys. Lett. 11, 745.CrossRefGoogle Scholar
[14]LaHaye, R. J. and Scoville, J. T. 1991 Rev. Sci. Instrum. 62, 2146.Google Scholar
[15]Punjabi, A., Verma, A. and Boozer, A. 1992 Phys. Rev. Lett. 69, 3322.CrossRefGoogle Scholar
[16]Punjabi, A., Ali, H., Evans, T. E. and Boozer, A. 2007 Phys. Lett. A 364, 140.Google Scholar
[17]Cartwright, J. and Piro, O. 1992 Int. J. Bifurcation Chaos 2, 427.Google Scholar
[18]Kolmogorov, A. N. 1954 Dokl. Akad. Nauk SSSR 98, 527.Google Scholar
[19]Arnold, V. I. 1962 Sov. Math. Dokl. 3, 136.Google Scholar
[20]Moser, J. 1962 Nachr. Akad. Wiss. Gottingen, Math. Phys. K1 12, 1.Google Scholar
[21]Ali, H., Punjabi, A., Boozer, A. and Evans, T. E. 2004 Phys. Plasmas 11, 1908.Google Scholar
[22]Punjabi, A., Ali, H. and Boozer, A. 1997 Phys. Plasmas 4, 337.Google Scholar
[23]Punjabi, A., Ali, H. and Boozer, A. 2003 Phys. Plasmas 4, 3992.CrossRefGoogle Scholar
[24]Eich, T., Herrmann, A., Neuhauser, J. and the ASDEX Upgrade Team 2003 Phys. Rev. Lett. 91, 195003.Google Scholar
[25]Eich, T. et al. Plasma Phys. Control. Fusion 47, 815.Google Scholar