Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T16:27:17.346Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical description of coalescing magnetic islands via magnetic reconnection

Part of: Focus on Plasma Astrophysics

Published online by Cambridge University Press:  21 December 2021

Muni Zhou Open the ORCID record for Muni Zhou [Opens in a new window] ,
David H. Wu Open the ORCID record for David H. Wu [Opens in a new window] ,
Nuno F. Loureiro Open the ORCID record for Nuno F. Loureiro [Opens in a new window]  and
Dmitri A. Uzdensky Open the ORCID record for Dmitri A. Uzdensky [Opens in a new window]
Muni Zhou*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
David H. Wu
Affiliation:
Department of Physics, California Institute of Technology, Pasadena, CA 91125, USA
Nuno F. Loureiro
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Dmitri A. Uzdensky
Affiliation:
Center for Integrated Plasma Studies, Physics Department, UCB-390, University of Colorado, Boulder, CO 80309, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The physical picture of interacting magnetic islands provides a useful paradigm for certain plasma dynamics in a variety of physical environments, such as the solar corona, the heliosheath and the Earth's magnetosphere. In this work, we derive an island kinetic equation to describe the evolution of the island distribution function (in area and in flux of islands) subject to a collisional integral designed to account for the role of magnetic reconnection during island mergers. This equation is used to study the inverse transfer of magnetic energy through the coalescence of magnetic islands in two dimensions. We solve our island kinetic equation numerically for three different types of initial distribution: Dirac delta, Gaussian and power-law distributions. The time evolution of several key quantities is found to agree well with our analytical predictions: magnetic energy decays as $\tilde {t}^{-1}$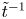, the number of islands decreases as $\tilde {t}^{-1}$ 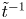and the averaged area of islands grows as $\tilde {t}$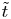, where $\tilde {t}$ 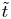is the time normalised to the characteristic reconnection time scale of islands. General properties of the distribution function and the magnetic energy spectrum are also studied. Finally, we discuss the underlying connection of our island-merger models to the (self-similar) decay of magnetohydrodynamic turbulence.

Keywords

astrophysical plasmasspace plasma physicsplasma nonlinear phenomena
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 6 , December 2021 , 905870620
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ball, D., Sironi, L. & Özel, F. 2018 Electron and proton acceleration in trans-relativistic magnetic reconnection: dependence on plasma beta and magnetization. Astrophys. J. 862 (1), 80.CrossRefGoogle Scholar
Bhat, P., Zhou, M. & Loureiro, N.F. 2021 Inverse energy transfer in decaying, three-dimensional, non-helical magnetic turbulence due to magnetic reconnection. Mon. Not. R. Astron. Soc. 501 (2), 3074–3087.CrossRefGoogle Scholar
Bhattacharjee, A., Huang, Y., Yang, H. & Rogers, B. 2009 Fast reconnection in high-Lundquist-number plasmas due to the plasmoid instability. Phys. Plasmas 16 (11), 112102.CrossRefGoogle Scholar
Birn, J., Drake, J.F., Shay, M.A., Rogers, B.N., Denton, R.E., Hesse, M., Kuznetsova, M., Ma, Z.W., Bhattacharjee, A., Otto, A., et al. 2001 Geospace Environmental Modeling (GEM) magnetic reconnection challenge. J. Geophys. Res. 106 (A3), 3715–3720.CrossRefGoogle Scholar
Biskamp, D., Schwarz, E. & Drake, J.F. 1995 Ion-controlled collisionless magnetic reconnection. Phys. Rev. Lett. 75 (21), 3850.CrossRefGoogle ScholarPubMed
Biskamp, D. & Welter, H. 1989 Dynamics of decaying two-dimensional magnetohydrodynamic turbulence. Phys. Fluids B 1 (10), 1964–1979.CrossRefGoogle Scholar
Boldyrev, S. & Loureiro, N.F. 2017 Magnetohydrodynamic turbulence mediated by reconnection. Astrophys. J. 844 (2), 125.CrossRefGoogle Scholar
Borg, A.L., Taylor, M. & Eastwood, J.P. 2012 Observations of magnetic flux ropes during magnetic reconnection in the Earth's magnetotail. Ann. Geophys. 30 (5), 761–773.CrossRefGoogle Scholar
Brandenburg, A. & Kahniashvili, T. 2017 Classes of hydrodynamic and magnetohydrodynamic turbulent decay. Phys. Rev. Lett. 118 (5), 055102.CrossRefGoogle ScholarPubMed
Brandenburg, A., Kahniashvili, T. & Tevzadze, A.G. 2015 Nonhelical inverse transfer of a decaying turbulent magnetic field. Phys. Rev. Lett. 114 (7), 075001.CrossRefGoogle ScholarPubMed
Burgers, J.M. 1948 A mathematical model illustrating the theory of turbulence. Advances in Applied Mechanics, vol. 1, pp. 171–199. Elsevier.Google Scholar
Cartwright, M.L. & Moldwin, M.B. 2010 Heliospheric evolution of solar wind small-scale magnetic flux ropes. J. Geophys. Res. 115 (A8), A08102.Google Scholar
Cassak, P.A., Liu, Y.H. & Shay, M.A. 2017 A review of the 0.1 reconnection rate problem. J. Plasma Phys. 83 (5), 715830501.CrossRefGoogle Scholar
Cassak, P.A. & Shay, M.A. 2007 Scaling of asymmetric magnetic reconnection: general theory and collisional simulations. Phys. Plasmas 14 (10), 102114.CrossRefGoogle Scholar
Cazzola, E., Curreli, D., Markidis, S. & Lapenta, G. 2016 On the ions acceleration via collisionless magnetic reconnection in laboratory plasmas. Phys. Plasmas 23 (11), 112108.CrossRefGoogle Scholar
Cerutti, B., Werner, G.R., Uzdensky, D.A. & Begelman, M.C. 2013 Simulations of particle acceleration beyond the classical synchrotron burnoff limit in magnetic reconnection: an explanation of the crab flares. Astrophys. J. 770, 147.CrossRefGoogle Scholar
Christensson, M., Hindmarsh, M. & Brandenburg, A. 2001 Inverse cascade in decaying three-dimensional magnetohydrodynamic turbulence. Phys. Rev. E 64 (5), 056405.CrossRefGoogle ScholarPubMed
Comisso, L., Huang, Y.-M., Lingam, M., Hirvijoki, E. & Bhattacharjee, A. 2018 Magnetohydrodynamic turbulence in the plasmoid-mediated regime. Astrophys. J. 854 (2), 103.CrossRefGoogle Scholar
Dahlin, J.T., Drake, J.F. & Swisdak, M. 2014 The mechanisms of electron heating and acceleration during magnetic reconnection. Phys. Plasmas 21 (9), 092304.CrossRefGoogle Scholar
Dahlin, J.T., Drake, J.F. & Swisdak, M. 2017 The role of three-dimensional transport in driving enhanced electron acceleration during magnetic reconnection. Phys. Plasmas 24 (9), 092110.CrossRefGoogle Scholar
Daughton, W. & Karimabadi, H. 2007 Collisionless magnetic reconnection in large-scale electron-positron plasmas. Phys. Plasmas 14 (7), 072303.CrossRefGoogle Scholar
Daughton, W., Roytershteyn, V., Karimabadi, H., Yin, L., Albright, B.J., Bergen, B. & Bowers, K.J. 2011 Role of electron physics in the development of turbulent magnetic reconnection in collisionless plasmas. Nat. Phys. 7, 539–542.CrossRefGoogle Scholar
Dmitruk, P. & Gómez, D.O. 1999 Scaling law for the heating of solar coronal loops. Astrophys. J. Lett. 527, L63–L66.CrossRefGoogle ScholarPubMed
Dong, C., Wang, L., Huang, Y.-M., Comisso, L. & Bhattacharjee, A. 2018 Role of the plasmoid instability in magnetohydrodynamic turbulence. Phys. Rev. Lett. 121 (16), 165101.CrossRefGoogle ScholarPubMed
Drake, J.F., Opher, M., Swisdak, M. & Chamoun, J.N. 2010 A magnetic reconnection mechanism for the generation of anomalous cosmic rays. Astrophys. J. 709, 963–974.CrossRefGoogle Scholar
Drake, J.F., Swisdak, M. & Fermo, R. 2012 The power-law spectra of energetic particles during multi-island magnetic reconnection. Astrophys. J. Lett. 763 (1), L5.CrossRefGoogle Scholar
Drake, J.F., Swisdak, M., Schoeffler, K.M., Rogers, B.N. & Kobayashi, S. 2006 Formation of secondary islands during magnetic reconnection. Geophys. Res. Lett. 33, L13105.CrossRefGoogle Scholar
Einaudi, G. & Velli, M. 1999 The distribution of flares, statistics of magnetohydrodynamic turbulence and coronal heating. Phys. Plasmas 6, 4146–4153.CrossRefGoogle Scholar
Fermo, R.L., Drake, J.F. & Swisdak, M. 2010 A statistical model of magnetic islands in a current layer. Phys. Plasmas 17 (1), 010702.CrossRefGoogle Scholar
Fried, B.D. 1959 Mechanism for instability of transverse plasma waves. Phys. Fluids 2 (3), 337–337.CrossRefGoogle Scholar
Furno, I., Intrator, T.P., Hemsing, E.W., Hsu, S.C., Abbate, S., Ricci, P. & Lapenta, G. 2005 Coalescence of two magnetic flux ropes via collisional magnetic reconnection. Phys. Plasmas 12 (5), 055702.CrossRefGoogle Scholar
Galeev, A.A., Rosner, R. & Vaiana, G.S. 1979 Structured coronae of accretion disks. Astrophys. J. 229, 318–326.CrossRefGoogle Scholar
Galsgaard, K. & Nordlund, Å. 1996 Heating and activity of the solar corona 1. Boundary shearing of an initially homogeneous magnetic field. J. Geophys. Res. 101, 13445–13460.CrossRefGoogle Scholar
Gekelman, W., De Haas, T., Daughton, W., Van Compernolle, B., Intrator, T. & Vincena, S. 2016 Pulsating magnetic reconnection driven by three-dimensional flux-rope interactions. Phys. Rev. Lett. 116 (23), 235101.CrossRefGoogle ScholarPubMed
Gingell, I., Schwartz, S.J., Eastwood, J.P., Burch, J.L., Ergun, R.E., Fuselier, S., Gershman, D.J., Giles, B.L., Khotyaintsev, Y.V., Lavraud, B., et al. 2019 Observations of magnetic reconnection in the transition region of quasi-parallel shocks. Geophys. Res. Lett. 46 (3), 1177–1184.CrossRefGoogle Scholar
Gruzinov, A. 2001 Gamma-ray burst phenomenology, shock dynamo, and the first magnetic fields. Astrophys. J. Lett. 563 (1), L15.CrossRefGoogle Scholar
Guo, F., Li, X., Daughton, W., Kilian, P., Li, H., Liu, Y., Yan, W. & Ma, D. 2019 Determining the dominant acceleration mechanism during relativistic magnetic reconnection in large-scale systems. Astrophys. J. Lett. 879 (2), L23.CrossRefGoogle Scholar
Guo, F., Li, X., Daughton, W., Li, H., Kilian, P., Liu, Y., Zhang, Q. & Zhang, H. 2021 Magnetic energy release, plasma dynamics and particle acceleration during relativistic turbulent magnetic reconnection. ApJ 919, 111.CrossRefGoogle Scholar
Guo, F., Liu, Y., Daughton, W. & Li, H. 2015 Particle acceleration and plasma dynamics during magnetic reconnection in the magnetically dominated regime. Astrophys. J. 806 (2), 167.CrossRefGoogle Scholar
Hakobyan, H., Petropoulou, M., Spitkovsky, A. & Sironi, L. 2021 Secondary energization in compressing plasmoids during magnetic reconnection. ApJ 912, 48.CrossRefGoogle Scholar
Hatori, T. 1984 Kolmogorov-style argument for the decaying homogeneous MHD turbulence. J. Phys. Soc. Japan 53 (8), 2539–2545.CrossRefGoogle Scholar
Holman, G.D., Sui, L., Schwartz, R.A. & Emslie, A.G. 2003 Electron bremsstrahlung hard x-ray spectra, electron distributions, and energetics in the 2002 july 23 solar flare. Astrophys. J. Lett. 595, L97–L101.CrossRefGoogle Scholar
Hosking, D.N. & Schekochihin, A.A. 2021 Reconnection-controlled decay of magnetohydrodynamic turbulence and the role of invariants. Phys. Rev. X 11 (4), 041005.Google Scholar
Hu, Q., Chen, Y. & le Roux, J. 2019 Radial evolution of the properties of small-scale magnetic flux ropes in the solar wind. J. Phys.: Conf. Ser. 1332, 012005.Google Scholar
Hu, Q., Zheng, J., Chen, Y., le Roux, J. & Zhao, L. 2018 Automated detection of small-scale magnetic flux ropes in the solar wind: first results from the wind spacecraft measurements. Astrophys. J. Suppl. Ser. 239 (1), 12.CrossRefGoogle Scholar
Huang, Y. & Bhattacharjee, A. 2010 Scaling laws of resistive magnetohydrodynamic reconnection in the high-Lundquist-number, plasmoid-unstable regime. Phys. Plasmas 17 (6), 062104.CrossRefGoogle Scholar
Huang, Y. & Bhattacharjee, A. 2012 Distribution of plasmoids in high-Lundquist-number magnetic reconnection. Phys. Rev. Lett. 109 (26), 265002.CrossRefGoogle ScholarPubMed
Intrator, T.P., Sun, X., Dorf, L., Sears, J.A., Feng, Y., Weber, T.E. & Swan, H.O. 2013 Flux ropes and 3D dynamics in the relaxation scaling experiment. Plasma Phys. Control. Fusion 55 (12), 124005.CrossRefGoogle Scholar
Janvier, M., Démoulin, P. & Dasso, S. 2014 Are there different populations of flux ropes in the solar wind? Sol. Phys. 289 (7), 2633–2652.CrossRefGoogle Scholar
Jara-Almonte, J., Ji, H., Yamada, M., Yoo, J. & Fox, W. 2016 Laboratory observation of resistive electron tearing in a two-fluid reconnecting current sheet. Phys. Rev. Lett. 117 (9), 095001.CrossRefGoogle Scholar
Ji, H. & Daughton, W. 2011 Phase diagram for magnetic reconnection in heliophysical, astrophysical, and laboratory plasmas. Phys. Plasmas 18 (11), 111207.CrossRefGoogle Scholar
Kato, T.N. 2005 Saturation mechanism of the Weibel instability in weakly magnetized plasmas. Phys. Plasmas 12 (8), 080705.CrossRefGoogle Scholar
Kato, T.N. & Takabe, H. 2008 Nonrelativistic collisionless shocks in unmagnetized electron-ion plasmas. Astrophys. J. Lett. 681 (2), L93.CrossRefGoogle Scholar
Katz, B., Keshet, U. & Waxman, E. 2007 Self-similar collisionless shocks. Astrophys. J. 655 (1), 375.CrossRefGoogle Scholar
Klimchuk, J.A. 2006 On solving the coronal heating problem. Sol. Phys. 234 (1), 41–77.CrossRefGoogle Scholar
Klimchuk, J.A., Patsourakos, S. & Cargill, P.J. 2008 Highly efficient modeling of dynamic coronal loops. Astrophys. J. 682 (2), 1351–1362.CrossRefGoogle Scholar
Lapenta, G. 2008 Self-feeding turbulent magnetic reconnection on macroscopic scales. Phys. Rev. Lett. 100 (23), 235001.CrossRefGoogle ScholarPubMed
Lazar, M., Schlickeiser, R., Wielebinski, R. & Poedts, S. 2009 Cosmological effects of Weibel-type instabilities. Astrophys. J. 693 (2), 1133.CrossRefGoogle Scholar
Lazarian, A. & Opher, M. 2009 A model of acceleration of anomalous cosmic rays by reconnection in the heliosheath. Astrophys. J. 703, 8–21.CrossRefGoogle Scholar
Le, A., Egedal, J., Ohia, O., Daughton, W., Karimabadi, H. & Lukin, V.S. 2013 Regimes of the electron diffusion region in magnetic reconnection. Phys. Rev. Lett. 110 (13), 135004.CrossRefGoogle ScholarPubMed
Li, X., Guo, F., Li, H., Stanier, A. & Kilian, P. 2019 Formation of power-law electron energy spectra in three-dimensional low-$\beta$ magnetic reconnection. Astrophys. J. 884 (2), 118.CrossRefGoogle Scholar
Lingam, M. & Comisso, L. 2018 A maximum entropy principle for inferring the distribution of 3D plasmoids. Phys. Plasmas 25 (1), 012114.CrossRefGoogle Scholar
Linton, M.G. 2006 Reconnection of nonidentical flux tubes. J. Geophys. Res. 111 (A12), A12S09.Google Scholar
Linton, M.G., Dahlburg, R.B. & Antiochos, S.K. 2001 Reconnection of twisted flux tubes as a function of contact angle. Astrophys. J. 553 (2), 905.CrossRefGoogle Scholar
Liu, Y., Birn, J., Daughton, W., Hesse, M. & Schindler, K. 2014 Onset of reconnection in the near magnetotail: PIC simulations. J. Geophys. Res. 119 (12), 9773–9789.CrossRefGoogle Scholar
Liu, Y., Daughton, W., Karimabadi, H., Li, H. & Roytershteyn, V. 2013 Bifurcated structure of the electron diffusion region in three-dimensional magnetic reconnection. Phys. Rev. Lett. 110 (26), 265004.CrossRefGoogle ScholarPubMed
Loureiro, N.F. & Boldyrev, S. 2017 a Collisionless reconnection in magnetohydrodynamic and kinetic turbulence. Astrophys. J. 850 (2), 182.CrossRefGoogle Scholar
Loureiro, N.F. & Boldyrev, S. 2017 b Role of magnetic reconnection in magnetohydrodynamic turbulence. Phys. Rev. Lett. 118 (24), 245101.CrossRefGoogle ScholarPubMed
Loureiro, N.F., Samtaney, R., Schekochihin, A.A. & Uzdensky, D.A. 2012 Magnetic reconnection and stochastic plasmoid chains in high-Lundquist-number plasmas. Phys. Plasmas 19 (4), 042303.CrossRefGoogle Scholar
Loureiro, N.F., Schekochihin, A.A. & Cowley, S.C. 2007 Instability of current sheets and formation of plasmoid chains. Phys. Plasmas 14 (10), 100703–100703.CrossRefGoogle Scholar
Lyutikov, M., Sironi, L., Komissarov, S.S. & Porth, O. 2017 a Explosive X-point collapse in relativistic magnetically dominated plasma. J. Plasma Phys. 83 (6), 635830601.CrossRefGoogle Scholar
Lyutikov, M., Sironi, L., Komissarov, S.S. & Porth, O. 2017 b Particle acceleration in relativistic magnetic flux-merging events. J. Plasma Phys. 83 (6), 635830602.CrossRefGoogle Scholar
Mallet, A., Schekochihin, A.A. & Chandran, B.D.G. 2017 Disruption of sheet-like structures in alfvénic turbulence by magnetic reconnection. Mon. Not. R. Astron. Soc. 468 (4), 4862–4871.CrossRefGoogle Scholar
Matthaeus, W.H. & Lamkin, S.L. 1986 Turbulent magnetic reconnection. Phys. Fluids 29, 2513–2534.CrossRefGoogle Scholar
Medvedev, M.V., Fiore, M., Fonseca, R.A., Silva, L.O. & Mori, W.B. 2004 Long-time evolution of magnetic fields in relativistic gamma-ray burst shocks. Astrophys. J. Lett. 618 (2), L75.CrossRefGoogle Scholar
Medvedev, M.V. & Loeb, A. 1999 Generation of magnetic fields in the relativistic shock of gamma-ray burst sources. Astrophys. J. 526 (2), 697.CrossRefGoogle Scholar
Moldwin, M.B., Ford, S., Lepping, R., Slavin, J. & Szabo, A. 2000 Small-scale magnetic flux ropes in the solar wind. Geophys. Res. Lett. 27 (1), 57–60.CrossRefGoogle Scholar
Moldwin, M.B., Phillips, J.L., Gosling, J.T., Scime, E.E., McComas, D.J., Bame, S.J., Balogh, A. & Forsyth, R.J. 1995 Ulysses observation of a noncoronal mass ejection flux rope: evidence of interplanetary magnetic reconnection. J. Geophys. Res. 100 (A10), 19903–19910.CrossRefGoogle Scholar
Øieroset, M., Phan, T.D., Haggerty, C., Shay, M.A., Eastwood, J.P., Gershman, D.J., Drake, J.F., Fujimoto, M., Ergun, R.E., Mozer, F.S., et al. 2016 MMS observations of large guide field symmetric reconnection between colliding reconnection jets at the center of a magnetic flux rope at the magnetopause. Geophys. Res. Lett. 43 (11), 5536–5544.CrossRefGoogle Scholar
Olesen, P. 1997 Inverse cascades and primordial magnetic fields. Phys. Lett. B 398 (3–4), 321–325.CrossRefGoogle Scholar
Opher, M., Drake, J.F., Swisdak, M., Schoeffler, K.M., Richardson, J.D., Decker, R.B. & Toth, G. 2011 Is the magnetic field in the heliosheath laminar or a turbulent sea of bubbles? Astrophys. J. 734, 71.CrossRefGoogle Scholar
Parker, E.N. 1957 Sweet's mechanism for merging magnetic fields in conducting fluids. J. Geophys. Res. 62, 509–520.CrossRefGoogle Scholar
Parker, E.N. 1972 Topological dissipation and the small-scale fields in turbulent gases. Astrophys. J. 174, 499.CrossRefGoogle Scholar
Parker, E.N. 1983 a Magnetic neutral sheets in evolving fields. I – general theory. Astrophys. J. 264, 635–647.CrossRefGoogle Scholar
Parker, E.N. 1983 b Magnetic neutral sheets in evolving fields. II – formation of the solar corona. Astrophys. J. 264, 642.CrossRefGoogle Scholar
Parker, E.N. 1988 Nanoflares and the solar x-ray corona. Astrophys. J. 330, 474–479.CrossRefGoogle Scholar
Petropoulou, M., Giannios, D. & Sironi, L. 2016 Blazar flares powered by plasmoids in relativistic reconnection. Mon. Not. R. Astron. Soc. 462 (3), 3325–3343.CrossRefGoogle Scholar
Phan, T.D., Eastwood, J.P., Shay, M.A., Drake, J.F., Sonnerup, B.U. Ö., Fujimoto, M., Cassak, P.A., Øieroset, M., Burch, J.L., Torbert, R.B., et al. 2018 Electron magnetic reconnection without ion coupling in Earth's turbulent magnetosheath. Nature 557, 202–206.CrossRefGoogle ScholarPubMed
Pouquet, A. 1978 On two-dimensional magnetohydrodynamic turbulence. J. Fluid Mech. 88 (1), 1–16.CrossRefGoogle Scholar
Retinò, A., Sundkvist, D., Vaivads, A., Mozer, F., André, M. & Owen, C.J. 2007 In situ evidence of magnetic reconnection in turbulent plasma. Nat. Phys. 3, 236–238.CrossRefGoogle Scholar
Ruyer, C. & Fiuza, F. 2018 Disruption of current filaments and isotropization of the magnetic field in counterstreaming plasmas. Phys. Rev. Lett. 120, 245002.CrossRefGoogle ScholarPubMed
Samtaney, R., Loureiro, N.F., Uzdensky, D.A., Schekochihin, A.A. & Cowley, S.C. 2009 Formation of plasmoid chains in magnetic reconnection. Phys. Rev. Lett. 103 (10), 105004.CrossRefGoogle ScholarPubMed
Schekochihin, A.A. 2020 Mhd turbulence: a biased review. arXiv:2010.00699.Google Scholar
Schlickeiser, R. & Shukla, P.K. 2003 Cosmological magnetic field generation by the Weibel instability. Astrophys. J. Lett. 599 (2), L57–L60.CrossRefGoogle Scholar
Schoeffler, K.M., Drake, J.F. & Swisdak, M. 2011 The effects of plasma beta and anisotropy instabilities on the dynamics of reconnecting magnetic fields in the heliosheath. Astrophys. J. 743 (1), 70.CrossRefGoogle Scholar
Shay, M.A., Drake, J.F., Rogers, B.N. & Denton, R.E. 2001 Alfvénic collisionless magnetic reconnection and the hall term. J. Geophys. Res. 106 (A3), 3759–3772.CrossRefGoogle Scholar
Silva, L.O., Fonseca, R.A., Tonge, J.W., Dawson, J.M., Mori, W.B. & Medvedev, M.V. 2003 Interpenetrating plasma shells: near-equipartition magnetic field generation and nonthermal particle acceleration. Astrophys. J. Lett. 596 (1), L121.CrossRefGoogle Scholar
Sironi, L., Giannios, D. & Petropoulou, M. 2016 Plasmoids in relativistic reconnection, from birth to adulthood: first they grow, then they go. Mon. Not. R. Astron. Soc. 462 (1), 48–74.CrossRefGoogle Scholar
Sironi, L. & Spitkovsky, A. 2014 Relativistic reconnection: an efficient source of non-thermal particles. Astrophys. J. Lett. 783 (1), L21.CrossRefGoogle Scholar
Spitkovsky, A. 2008 On the structure of relativistic collisionless shocks in electron-ion plasmas. Astrophys. J. Lett. 673 (1), L39.CrossRefGoogle Scholar
Stone, E.C., Cummings, A.C., McDonald, F.B., Heikkila, B.C., Lal, N. & Webber, W.R. 2005 Voyager 1 explores the termination shock region and the heliosheath beyond. Science 309, 2017–2020.CrossRefGoogle ScholarPubMed
Stone, E.C., Cummings, A.C., McDonald, F.B., Heikkila, B.C., Lal, N. & Webber, W.R. 2008 An asymmetric solar wind termination shock. Nature 454, 71–74.CrossRefGoogle ScholarPubMed
Sweet, P.A. 1958 The Neutral Point Theory of Solar Flares. In Electromagnetic Phenomena in Cosmical Physics (ed. B. Lehnert), IAU Symposium, vol. 6, p. 123. Cambridge University Press.CrossRefGoogle Scholar
Taylor, J.B. 1974 Relaxation of toroidal plasma and generation of reverse magnetic fields. Phys. Rev. Lett. 33 (19), 1139.CrossRefGoogle Scholar
Uzdensky, D.A. 2020 Relativistic nonthermal particle acceleration in two-dimensional collisionless magnetic reconnection. arXiv:2007.09533.Google Scholar
Uzdensky, D.A. & Goodman, J. 2008 Statistical description of a magnetized corona above a turbulent accretion disk. Astrophys. J. 682, 608–629.CrossRefGoogle Scholar
Uzdensky, D.A., Loureiro, N.F. & Schekochihin, A.A. 2010 Fast magnetic reconnection in the plasmoid-dominated regime. Phys. Rev. Lett. 105 (23), 235002.CrossRefGoogle ScholarPubMed
Wang, Y. & Sheeley, N. Jr. 2006 Observations of flux rope formation in the outer corona. Astrophys. J. 650 (2), 1172.CrossRefGoogle Scholar
Weibel, E.S. 1959 Spontaneously growing transverse waves in a plasma due to an anisotropic velocity distribution. Phys. Rev. Lett. 2 (3), 83.CrossRefGoogle Scholar
Werner, G.R., Uzdensky, D.A., Begelman, M.C., Cerutti, B. & Nalewajko, K. 2018 Non-thermal particle acceleration in collisionless relativistic electron-proton reconnection. Mon. Not. R. Astron. Soc. 473 (4), 4840–4861.CrossRefGoogle Scholar
Werner, G.R., Uzdensky, D.A., Cerutti, B., Nalewajko, K. & Begelman, M.C. 2016 The extent of power-law energy spectra in collisionless relativistic magnetic reconnection in pair plasmas. Astrophys. J. Lett. 816, L8.CrossRefGoogle Scholar
Yamada, M., Ji, H., Hsu, S., Carter, T., Kulsrud, R., Bretz, N., Jobes, F., Ono, Y. & Perkins, F. 1997 Study of driven magnetic reconnection in a laboratory plasma. Phys. Plasmas 4 (5), 1936–1944.CrossRefGoogle Scholar
Zhang, J., Cheng, X. & Ding, M. 2012 Observation of an evolving magnetic flux rope before and during a solar eruption. Nat. Commun. 3 (1), 1–6.CrossRefGoogle ScholarPubMed
Zhou, M., Bhat, P., Loureiro, N.F. & Uzdensky, D.A. 2019 Magnetic island merger as a mechanism for inverse magnetic energy transfer. Phys. Rev. Res. 1, 012004.CrossRefGoogle Scholar
Zhou, M., Loureiro, N.F. & Uzdensky, D.A. 2020 Multi-scale dynamics of magnetic flux tubes and inverse magnetic energy transfer. J. Plasma Phys. 86 (4), 535860401.CrossRefGoogle Scholar
Zhou, M., Zhdankin, V., Kunz, M.W., Loureiro, N.F. & Uzdensky, D.A. 2021 Spontaneous magnetization of collisionless plasma through the action of a shear flow. arXiv:2110.01134.Google Scholar
Zrake, J. 2014 Inverse cascade of nonhelical magnetic turbulence in a relativistic fluid. Astrophys. J. Lett. 794 (2), L26.CrossRefGoogle Scholar
Zrake, J. & Arons, J. 2017 Turbulent magnetic relaxation in pulsar wind nebulae. Astrophys. J. 847 (1), 57.CrossRefGoogle Scholar