Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T07:06:24.266Z Has data issue: false hasContentIssue false
  • English
  • Français

Shielding of moving test particles in warm, isotropic plasma

Published online by Cambridge University Press:  13 March 2009

Liu Chen ,
A. Bruce Landon  and
M. A. Lieberman
Liu Chen
Affiliation:
Department of Electrical Engineering and Computer Sciences, University of California, Berkeley
A. Bruce Landon
Affiliation:
Department of Electrical Engineering and Computer Sciences, University of California, Berkeley
M. A. Lieberman
Affiliation:
Department of Electrical Engineering and Computer Sciences, University of California, Berkeley
Get access Rights & Permissions [Opens in a new window]

Abstract

Shielding of test charges in warm, isotropic electron and electron–ion (Te ≫ Ti) plasmas is studied analytically and numerically. For a plasma with hot Maxwellian electrons and cold mobile ions, the potential due to a charge moving faster than the ion acoustic velocity has an ion acoustic Cerenkov cone. Ahead of the particle, the shielding is the usual electron Debye type with a modified longer shielding length. Potential wells with γ−1 dependence exists inside the cone. 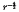The potential falls off as along the cone surface. Outside the cone, the potential decays exponentially. A charge moving slower than the ion acoustic velocity also creates a cone, with potential decay as γ−3 outside the cone, potential wells decaying as γ−1 inside the cone, and potential wells falling off as 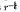along the cone surface. In both cases a radial logarithmic singularity exists along the trailing axis. Using a mono-energetic ion distribution, the singularity is removed and an ion thermal Cerenkov cone appears. For a monoenergetic electron plasma, assuming immobile ions, a test charge moving faster than the electron thermal velocity excites a thermal Cerenkov cone. Outside the cone, the far-field potential falls off in quadrupole form as γ−3. Inside the cone, potential wells decay as γ−1.

Type
Research Article
Information
Journal of Plasma Physics , Volume 9 , Issue 3 , June 1973 , pp. 311 - 324
Copyright
Copyright © Cambridge University Press 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Alexeff, I. & Estabrook, K. 1971 Bull. Am. Phys. Soc. 16, 1279.Google Scholar
Cooper, G. 1969 Phys. Fluids, 12, 2707.CrossRefGoogle Scholar
Joyce, G. & Montgomery, D. 1967 Phys. Fluids, 10, 2017.CrossRefGoogle Scholar
Montgomery, D., Joyce, G. & Sagihara, R. 1968 Plasma Phys. 10, 681.CrossRefGoogle Scholar
Neufeld, J. & Ritchie, R. H. 1955 Phys. Rev. 98, 1635.CrossRefGoogle Scholar
Rostoker, N. 1960 Nuclear Fusion, 1, 101.CrossRefGoogle Scholar
Sanmartin, J. R. & Lam, S. H. 1971 Phys. Fluids, 14 62.CrossRefGoogle Scholar
Thompson, W. B. 1962 An Introduction to Plasma Physics. Pergamon.CrossRefGoogle Scholar