Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T05:20:54.234Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-gravitational instability of dense degenerate viscous anisotropic plasma with rotation

Published online by Cambridge University Press:  06 November 2017

Prerana Sharma  and
Archana Patidar
Prerana Sharma*
Affiliation:
Physics Department, Ujjain Engineering College, Ujjain, M. P. - 456010, India
Archana Patidar
Affiliation:
Physics Department, Ujjain Engineering College, Ujjain, M. P. - 456010, India
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The influence of finite Larmor radius correction, tensor viscosity and uniform rotation on self-gravitational and firehose instabilities is discussed in the framework of the quantum magnetohydrodynamic and Chew–Goldberger–Low (CGL) fluid models. The general dispersion relation is obtained for transverse and longitudinal modes of propagation. In both the modes of propagation the dispersion relation is further analysed with respect to the direction of the rotational axis. In the analytical discussion the axis of rotation is considered in parallel and in the perpendicular direction to the magnetic field. (i) In the transverse mode of propagation, when rotation is parallel to the direction of the magnetic field, the Jeans instability criterion is affected by the rotation, finite Larmor radius (FLR) and quantum parameter but remains unaffected due to the presence of tensor viscosity. The calculated critical Jeans masses for rotating and non-rotating dense degenerate plasma systems are 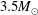$3.5M_{\odot }$ and 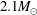$2.1M_{\odot }$ respectively. It is clear that the presence of rotation enhances the threshold mass of the considered system. (ii) In the case of longitudinal mode of propagation when rotation is parallel to the direction of the magnetic field, Alfvén and viscous self-gravitating modes are obtained. The Alfvén mode is modified by FLR corrections and rotation. The analytical as well as graphical results show that the presence of FLR and rotation play significant roles in stabilizing the growth rate of the firehose instability by suppressing the parallel anisotropic pressure. The viscous self-gravitating mode is significantly affected by tensor viscosity, anisotropic pressure and the quantum parameter while it remains free from rotation and FLR corrections. When the direction of rotation is perpendicular to the magnetic field, the rotation of the considered system coupled the Alfvén and viscous self-gravitating modes to each other. The finding of the present work is applicable to strongly magnetized dense degenerate plasma.

Keywords

astrophysical plasmasmagnetized plasmasplasma instabilities
Type
Research Article
Information
Journal of Plasma Physics , Volume 83 , Issue 6 , December 2017 , 905830601
Copyright
© Cambridge University Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bhatiya, P. K. 1968a Effect of finite Larmor radius on gravitational instability of a plasma. Zitschift Fur Astrophysik 68, 204.Google Scholar
Bhatiya, P. K. 1968b Gravitational instability of a rotating anisotropic plasma with the inclusion of finite Larmor radius effect. Zitschift Fur Astrophysik 69, 363–367.Google Scholar
Campos, L. M. B. C. & Mendes, P. M. V. M. 2000 On the effect of viscosity and anisotropic resistivity on the damping of Alfven waves. J. Plasma Phys. 63, 221–238.CrossRefGoogle Scholar
Chandrashekhar, S. 1931 The maximum mass of ideal white dwarfs. Astrophys. J. 74, 81.CrossRefGoogle Scholar
Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability, p. 585. Oxford University.Google Scholar
Cherkos, A. M. & Tessema, S. B. 2013 Gravitational instability on propagation of MHD waves in astrophysical plasma. J. Plasma Phys. 79, 805–816.CrossRefGoogle Scholar
Chew, G. F., Goldberger, L. & Low, F. E. 1956 The Boltzmann equation and the one fluid hydrodynamic equation in the absence of particle collisions. Math. Phys. Sci. 236, 112–118.Google Scholar
Craighead, H. G. 2000 Nanoelectromechanical systems. Sciences 290, 1532–1536.CrossRefGoogle ScholarPubMed
Das, U. & Mukhopadhyay, B. 2015 GRMHD formulation of highly super-Chandrashekhar magnetized white dwarfs: stable configurations of non-spherical white dwarfs. J. Cosmol. Astropart. Phys. 05, 016.Google Scholar
Dzhalilov, N. S., Kuznetsov, V. D. & Staude, J. 2011 Wave instabilities of a collisionless plasma in fluid approximation contrib. Plasma Phys. 51, 621–638.Google Scholar
Franzon, B. & Schramm, S. 2015 Effects of strong magnetic fields and rotation on white dwarf structure. Phys. Rev. D 92, 083006.Google Scholar
Glentzer, S. H., Landen, O. L., Neumayer, P., Lee, R. W., Wldmann, K., Pollaine, S. W., Wallance, R. J., Gregori, G., Holl, A., Bomath, T. et al. 2007 Observations of Plasmons in warm dense matter. Phys. Rev. Lett. 98, 065002.CrossRefGoogle Scholar
Gliddon, J. E. C. 1966 Gravitational Instability of Anisotropic plasma. Astrophys. J. 145, 583–588.CrossRefGoogle Scholar
Haas, F. 2005 A magnetohydrodynamic model for quantum plasmas. Phys. Plasmas 12, 062117.CrossRefGoogle Scholar
Hollweg, J. V. 1987 Resonance absorption of magnetohydrodynamic surface waves: viscous effects. Astro. Phys. J. 320, 875–883.CrossRefGoogle Scholar
Howell, D. A., Sullivan, M., Nugent, P. E., Ellis, R. S., Conley, A. J., Borgne, D. L., Carlberg, R. G., Guy, J., Balam, D., Basa, S. et al. 2006 The type Ia supernova SNLS-03D3bb from a super-Chandrasekhar-mass white dwarf star. Nature 443, 308–311.CrossRefGoogle ScholarPubMed
Ida, K. & Rice, J. E. 2014 Rotation and momentum transport in tokamaks and helical systems. Nucl. Fusion 54, 4.CrossRefGoogle Scholar
Irfan, M., Ali, S. & Mirza, M. A. 2017 Solitary waves in a degenerate relativistic plasma with ionic pressure anisotropic and electron trapping effects. Phys. Plasmas 24, 052108.CrossRefGoogle Scholar
Jain, S., Sharma, P. & Chhajlani, R. K. 2015 Jeans instability of magnetized quantum plasma: effect of viscosity, rotation and finite Larmor radius corrections. AIP Conf. Proc. 1670, 030013.CrossRefGoogle Scholar
Jeans, J. H. 1929 Astronomy and Cosmology, pp. 345–347. Cambridge University Press.Google Scholar
Jung, Y. F. 2001 Quantum-mechanical effects on electron–electron scattering in dense high-temperature plasmas. Phys. Plasmas 6, 3842.CrossRefGoogle Scholar
Kato, S. & Kumar, S. S. 1960 On gravitational instability. II. Pub. Astro. Soc. Japan 12, 290–292.Google Scholar
Kumar, S. S. 1960 On gravitational instability. II. Smithsonian Astrophysical Observatory 12, 4.Google Scholar
Lundin, J., Marklund, M. & Brodin, G. 2008 Modified Jeans instability criteria for magnetized system. Phys. Plasmas 15, 7.CrossRefGoogle Scholar
Mahmood, S., Hussain, S., Masood, W. & Saleem, H. 2009 Nonlinear electrostatic waves in anisotropic ion pressure plasmas. Phys. Scr. 79, 045501.CrossRefGoogle Scholar
Manfredi, G. 2005 How to model quantum plasma. Fields Inst. Commun. 46, 263.Google Scholar
Markovich, P. A., Ringhofer, C. A. & Schmeiser, C. 1990 Semiconductor Equations. Springer-Verlag.CrossRefGoogle Scholar
Cherkos, A. & Tessema, S. B. 2013 Effect of viscosity on propagation of MHD waves in astrophysical plasma. J. Plasma Phys. 79, 535–544.CrossRefGoogle Scholar
Mushtaq, A. & Vladimirov, S. V. 2011 Arbitrary magnetosonic solitary waves in spin 1/2 degenerate quantum plasma. Eur. Phys. J. D. 64, 419–426.CrossRefGoogle Scholar
Opher, M., Silva, L. O., Danger, D. E., Decyk, V. K. & Dawson, J. 2001 Nuclear reaction rates and energy in stellar plasmas: the effect of highly damped modes. Phys. Plasmas 8, 2454.CrossRefGoogle Scholar
Pandey, V. S. & Dwivedi, B. N. 2007 Dispersion relation for MHD waves in homogeneous plasma. J. Bull. Astron. Soc. India 35, 465.Google Scholar
Paret, D. M., Martinez, A. P. & Horvath, J. E.2015 Maximum mass of white dwarfs. arXiv:1501.04619v1 [astro-ph.HE].Google Scholar
Pines, D. 1961 Classical and quantum plasmas. J. Nucl. Energy 2, 5–17.CrossRefGoogle Scholar
Prajapati, R. P. 2014 Low frequency waves and gravitational instability in homogeneous magnetized gyrotropic quantum plasma. Phys. Plasmas 21, 112101.CrossRefGoogle Scholar
Prajapati, R. P., Parihar, A. K. & Chhajlani, R. K. 2008 Self-gravitational instability of rotating anisotropic heat-conducting plasma. Phys. Plasmas 15, 012107.CrossRefGoogle Scholar
Ren, H., Wu, Z., Cao, J. & Chu, P. K. 2009 Jeans instability in quantum magnetoplasma with resistive effects. Phys. Plasmas 16, 072101.Google Scholar
Roberts, K. V. & Taylor, J. B. 1962 Magnetohydrodynamic equations for finite Larmor radius. Phys. Rev. Lett. 8, 5.CrossRefGoogle Scholar
Roxburgh, I. W. 1965 On models of non-spherical stars II. Rotating white dwarfs. Zitschift Fur Astrophysik 62, 134–142.Google Scholar
Scalzo, R. A., Aldering, G., Antilogus, P., Aragon, C., Bailey, S., Baltay, C., Bongard, S., Buton, C. M., Childress, M., Chotard, N. et al. 2010 Nearby supernova factory observations of SN 2007IF: first total mass measurement of a super-Chandrashekhar mass progenitor. Astrophys. J. 713, 1073.CrossRefGoogle Scholar
Sharma, P. 2017 Structure formation through self-gravitational instability in degenerate and non-degenerate anisotropic magnetized plasma. Astron. Phys. Space Sci. 362, 4.Google Scholar
Sharma, P. K., Argal, S., Tiwari, A. & Prajapati, R. P. 2015 Jeans instability of rotating viscoelastic fluid in the presence of magnetic field. Z. Naturforsch. 70, 39–45.CrossRefGoogle Scholar
Sharma, P. & Chhajlani, R. K. 2013 The effect of finite Larmor radius corrections on Jeans instability of quantum plasma. Phys. Plasmas 20, 9.CrossRefGoogle Scholar
Shukla, P. K. & Eliasson, B.2009 Nonlinear aspects of quantum plasma physics arXiv:0906.4051v4 [physics.plasm-ph].Google Scholar
Shukla, P. K. & Stenflo, L. 2008 Quantum Hall-MHD equations for a non-uniform dense magnetoplasma with electron temperature anisotropy. J. Plasma Phys. 74, 575.CrossRefGoogle Scholar
Singh, B. & Kalra, G. L. 1986 Gravitational instability of therally anisotropic plasma. Astrophys. J. 304, 6–10.CrossRefGoogle Scholar
Strait, E. J., Garofalo, A. M., Jackson, G. L., Okabayashi, M., Reimerdes, H., Chu, M. S., Fitzpatrick, R., Groebner, R. J., In, Y., Lahaye, R. J. et al. 2007 Resistive wall mode stabilization by slow plasma rotation in DIII-D Tokamak discharges with balanced neutral beam injection. Phys. Plasmas 14, 056101.CrossRefGoogle Scholar
Subramanian, S. & Mukhopadhyay, B. 2015 GRMHD formulation of highly super-Chandrasekhar rotating magnetised white dwarfs: stable configurations of non-spherical white dwarfs. J. Cosmol. Astropart. Phys. 2015, 016.Google Scholar
Tessema, S. B. & Torkelsson, U. 2010 The structure of thin accretion discs around magnetized stars. J. Astron. Astrophys. A45, 509.Google Scholar
Wu, Z., Ren, H., Cao, J. & Chu, P. K. 2010 The effect of Hall term on Jeans instability in quantum magnetoplasma with resistivity effects. Phys. Plasmas 17, 064503.CrossRefGoogle Scholar
Yajima, N. 1966 The effect of finite ion Larmor radius on the propagation of magnetosonic waves. Prog. Theor. Phys. 36, 1.CrossRefGoogle Scholar
Yamanaka, M., Kawabata, K. S., Kinugasa, K., Tanaka, M., Imada, A., Maeda, K., Nomoto, K., Arai, A., Chiyonobu, S., Fukazawa, Y. et al. 2009 Early phase observations of extremely luminous type IA supernova 2009dc. Astrophys. J. Lett. 707, L118–L122.CrossRefGoogle Scholar
Yoon, S. C. & Langer, N. 2005 On the evolution of rapidly rotating massive white dwarfs towards supernovae or collapses. Astron. Astrophys. 435, 967–985.CrossRefGoogle Scholar