Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T06:43:36.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Self-consistent Vlasov equilibria for intense hollow relativistic electron beams

Published online by Cambridge University Press:  13 March 2009

R. C. Davidson  and
C. D. Striffler
R. C. Davidson
Affiliation:
Department of Physics and Astronomy, University of Maryland, College Park, Maryland 20742
C. D. Striffler
Affiliation:
Naval Research Laboratory, Washington, D.C. 20390
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper discusses the procedure for constructing intense hollow relativistic electron beam equilibria within the framework of the steady-state (∂/∂t = 0) Vlasov–Maxwell equations. It is assumed that the electron beam propagates parallel to a uniform axial guide field Bext0 = B0 êz inside a grounded cylindrical conductor, and that the positive ions provide a partially neutralizing background with density n0i(r) = fn0e(r), where f = const. = fractional neutralization. The equilibrium properties are calculated for the specific choice of electron distribution function 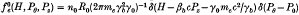, where H, Pθ, and Pz are the energy, canonical angular momentum, and axialcanonical momentum, respectively, for an electron moving in the equilibrium fields, and 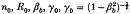, and P0 are constants. For this choice of distribution function, the mean axial velocity of the electron beam is equal to 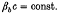, and the beam density profile 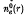is hollow with inner and outer radii, R0 and R1, determined self-consistently from nonlinear boundary conditions that involve the equilibrium parameters Po, γb, γ0, etc., and the equilibrium self fields. Closed expressions for Ro and B1 are obtained for the case where the collisionless skin depth c/ωpe is large in comparison with the characteristic radius of the electron beam, and the beam density is sufficiently low that 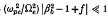. The two cases, Po>0 and Po<0, are considered.

Type
Research Article
Information
Journal of Plasma Physics , Volume 12 , Issue 3 , December 1974 , pp. 353 - 364
Copyright
Copyright © Cambridge University Press 1974

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bennett, W. H. 1934 Phys Rev. 45, 890.CrossRefGoogle Scholar
Bennett, W. H. 1955 Phys. Rev. 98, 1584.CrossRefGoogle Scholar
Bogdankevich, L. S.& Rukhadze, A. A. 1971 Soviet Phys. Uspekhi, 14, 153.CrossRefGoogle Scholar
Davidson, R. C.& Krall, N. A. 1970 Phys. Fluids, 13, 1543.CrossRefGoogle Scholar
Davidson, R. C.& Lawson, S. D. 1972 Particle Accelerators, 4, 1.Google Scholar
Hammer, D. A.& Rostoker, N. 1970 Phys. Fluids, 13, 1831.CrossRefGoogle Scholar
Kapetanakos, C. A.& Hammer, D. A. 1973 Appl. Phys. Letters, 23, 17.CrossRefGoogle Scholar
Kapatenakos, C. A., Hammer, D. A., Striffler, C. D.& Davidson, R. C. 1973 Phys. Rev. Letters, 30, 1303.CrossRefGoogle Scholar