Article contents
Reimagining full wave rf quasilinear theory in a tokamak
Published online by Cambridge University Press: 12 April 2021
Abstract
The velocity dependent resonant interaction of particles with applied radiofrequency (rf) waves during heating and current drive in the presence of pitch angle scattering collisions gives rise to narrow collisional velocity space boundary layers that dramatically enhance the role of collisions as recently shown by Catto (J. Plasma Phys., vol. 86, 2020, 815860302). The behaviour is a generalization of the narrow collisional boundary layer that forms during Landau damping as found by Johnston (Phys. Fluids, vol. 14, 1971, pp. 2719–2726) and Auerbach (Phys. Fluids, vol. 20, 1977, pp. 1836–1844). For a wave of parallel wave number 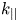 ${k_{||}}$ interacting with weakly collisional plasma species of collision frequency
${k_{||}}$ interacting with weakly collisional plasma species of collision frequency 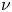 $\nu$ and thermal speed
$\nu$ and thermal speed 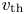 ${v_{\textrm{th}}}$, the effective collision frequency becomes of order
${v_{\textrm{th}}}$, the effective collision frequency becomes of order 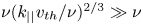 $\nu {({k_{||}}{v_{th}}/\nu )^{2/3}} \gg \nu $. The narrow boundary layers that arise because of the diffusive nature of the collisions allow a physically meaningful wave–particle interaction time to be defined that is the inverse of this effective collision frequency. The collisionality implied by the narrow boundary layer results in changes in the standard quasilinear treatment of applied rf fields in tokamaks while remaining consistent with causality. These changes occur because successive poloidal interactions with the rf are correlated in tokamak geometry and because the resonant velocity space dependent interactions are controlled by the spatial and temporal behaviour of the perturbed full wave fields rather than just the spatially local Landau and Doppler shifted cyclotron wave–particle resonance condition associated with unperturbed motion of the particles. The correlation of successive poloidal circuits of the tokamak leads to the appearance in the quasilinear operator of transit averaged resonance conditions localized in velocity space boundary layers that maintain negative definite entropy production.
$\nu {({k_{||}}{v_{th}}/\nu )^{2/3}} \gg \nu $. The narrow boundary layers that arise because of the diffusive nature of the collisions allow a physically meaningful wave–particle interaction time to be defined that is the inverse of this effective collision frequency. The collisionality implied by the narrow boundary layer results in changes in the standard quasilinear treatment of applied rf fields in tokamaks while remaining consistent with causality. These changes occur because successive poloidal interactions with the rf are correlated in tokamak geometry and because the resonant velocity space dependent interactions are controlled by the spatial and temporal behaviour of the perturbed full wave fields rather than just the spatially local Landau and Doppler shifted cyclotron wave–particle resonance condition associated with unperturbed motion of the particles. The correlation of successive poloidal circuits of the tokamak leads to the appearance in the quasilinear operator of transit averaged resonance conditions localized in velocity space boundary layers that maintain negative definite entropy production.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
- 5
- Cited by



