Article contents
On the accuracy of the binary-collision algorithm in particle-in-cell simulations of magnetically confined fusion plasmas
Published online by Cambridge University Press: 19 April 2021
Abstract
Ideally, binary-collision algorithms conserve kinetic momentum and energy. In practice, the finite size of collision cells and the finite difference in the particle locations affect the conservation properties. In the present work, we investigate numerically how the accuracy of these algorithms is affected when the size of collision cells is large compared with gradient scale length of the background plasma, a parameter essential in full-$f$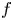 fusion plasma simulations. Additionally, we discuss implications for the conserved quantities in drift-kinetic formulations when fluctuating magnetic and electric fields are present: we suggest how the accuracy of the algorithms could potentially be improved with minor modifications.
fusion plasma simulations. Additionally, we discuss implications for the conserved quantities in drift-kinetic formulations when fluctuating magnetic and electric fields are present: we suggest how the accuracy of the algorithms could potentially be improved with minor modifications.
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 5
- Cited by



