Article contents
A numerical investigation of magnetic reconnection
Published online by Cambridge University Press: 13 March 2009
Abstract
A time-dependent two-dimensional MHD simulation program is used to investigate the magnetic reconnection process with a spatially uniform diffusivity. Various initial conditions are considered and are allowed to evolve until a final steady state is produced. The boundary conditions are carefully handled in order that they be as strict as possible. In the first series of simulations the initial condition is taken to be an analytical solution of the ideal MHD equations given by Biskamp. Dirichlet (fixed) boundary conditions are used, with a small amount of flexibility allowed on the boundary for the stream function in order to prevent any unphysical currents forming. The final steady- state contains a current sheet whose width and length are found to vary as 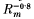 and
and 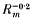 respectively, and the reconnection rate is found to be independent of the value of Rm, indicative of fast reconnection. Additionally, as Rm, is increased, a region of reversed current and a high-speed jet of plasma are observed to develop along the MHD shock separating the inflow and outflow regions. The second series of simulations uses a slightly different initial condition that allows a faster outflow of plasma from the simulation region. The current sheet width of the final steady state is again found to vary as
respectively, and the reconnection rate is found to be independent of the value of Rm, indicative of fast reconnection. Additionally, as Rm, is increased, a region of reversed current and a high-speed jet of plasma are observed to develop along the MHD shock separating the inflow and outflow regions. The second series of simulations uses a slightly different initial condition that allows a faster outflow of plasma from the simulation region. The current sheet width of the final steady state is again found to vary as 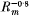 , and the reconnection rate is again independent of Rm. However, no reversed currents or plasma jetting along the shock are observed, indicating that the plasma jets of previous simulations are due to restrictive outflow conditions, which force the high-speed plasma emerging from the end of the current sheet to divert along the MHD shock. Lastly, the analytical model of Petschek is utilized to provide an initial condition. For this case, however, it is not possible to keep the boundary conditions as strict as before, since both the stream and flux functions have to be allowed to vary slightly in order to deal with the discontinuities of the Petschek model. Although steady-state solutions can be obtained, they are found, owing to the laxness of the boundary conditions, not to exhibit the well-defined structure or small current sheets of the previous results.
, and the reconnection rate is again independent of Rm. However, no reversed currents or plasma jetting along the shock are observed, indicating that the plasma jets of previous simulations are due to restrictive outflow conditions, which force the high-speed plasma emerging from the end of the current sheet to divert along the MHD shock. Lastly, the analytical model of Petschek is utilized to provide an initial condition. For this case, however, it is not possible to keep the boundary conditions as strict as before, since both the stream and flux functions have to be allowed to vary slightly in order to deal with the discontinuities of the Petschek model. Although steady-state solutions can be obtained, they are found, owing to the laxness of the boundary conditions, not to exhibit the well-defined structure or small current sheets of the previous results.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1996
References
REFERENCES
- 2
- Cited by


