Published online by Cambridge University Press: 28 March 2019
In magnetized plasma situations where magnetic fields intersect massive conducting boundaries, ‘line-tied’ boundary conditions are often used, analytically and in numerical simulations. For ideal magnetohydrodynamic (MHD) plasmas, these conditions are arrived at given the relatively long time scales for magnetic fields penetrating resistively into good conductors. Under line-tied boundary conditions, numerical simulations often exhibit what could be construed as numerical ‘noise’ emanating from the boundaries. We show here that this ‘noise’ is real. By combining numerical and analytical methods, we highlight the existence of sharp spatial structures near the conductors and confirm the appearance of short wavelength structures riding on long wavelength modes. We conclude that, for numerical fidelity, the short multiscale structures need to be resolved. Generally, the short structure widths scale as the square root of the plasma 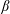 $\unicode[STIX]{x1D6FD}$.
$\unicode[STIX]{x1D6FD}$.