Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-24T19:46:07.642Z Has data issue: false hasContentIssue false
  • English
  • Français

Gyrofluid analysis of electron βe effects on collisionless reconnection

Published online by Cambridge University Press:  08 February 2022

C. Granier Open the ORCID record for C. Granier [Opens in a new window] ,
D. Borgogno Open the ORCID record for D. Borgogno [Opens in a new window] ,
D. Grasso Open the ORCID record for D. Grasso [Opens in a new window]  and
E. Tassi Open the ORCID record for E. Tassi [Opens in a new window]
C. Granier*
Affiliation:
Université Côte d'Azur, CNRS, Observatoire de la Côte d'Azur, Laboratoire J. L. Lagrange, Boulevard de l'Observatoire, CS 34229, 06304Nice Cedex 4, France Istituto dei Sistemi Complessi – CNR and Dipartimento di Energia, Politecnico di Torino, Torino10129, Italy
D. Borgogno
Affiliation:
Istituto dei Sistemi Complessi – CNR and Dipartimento di Energia, Politecnico di Torino, Torino10129, Italy
D. Grasso
Affiliation:
Istituto dei Sistemi Complessi – CNR and Dipartimento di Energia, Politecnico di Torino, Torino10129, Italy
E. Tassi
Affiliation:
Université Côte d'Azur, CNRS, Observatoire de la Côte d'Azur, Laboratoire J. L. Lagrange, Boulevard de l'Observatoire, CS 34229, 06304Nice Cedex 4, France
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The linear and nonlinear evolutions of the tearing instability in a collisionless plasma with a strong guide field are analysed on the basis of a two-field Hamiltonian gyrofluid model. The model is valid for a low ion temperature and a finite $\beta _e$. The finite $\beta _e$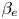 effect implies a magnetic perturbation along the guide field direction, and electron finite Larmor radius effects. A Hamiltonian derivation of the model is presented. A new dispersion relation of the tearing instability is derived for the case $\beta _e=0$ 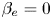and tested against numerical simulations. For $\beta _e \ll 1$ 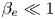the equilibrium electron temperature is seen to enhance the linear growth rate, whereas we observe a stabilizing role when electron finite Larmor radius effects become more relevant. In the nonlinear phase, stall phases and faster than exponential phases are observed, similarly to what occurs in the presence of ion finite Larmor radius effects. Energy transfers are analysed and the conservation laws associated with the Casimir invariants of the model are also discussed. Numerical simulations seem to indicate that finite $\beta _e$ 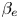effects do not produce qualitative modifications in the structures of the Lagrangian invariants associated with Casimirs of the model.

Keywords

astrophysical plasmasplasma instabilitiesspace plasma physics
Type
Research Article
Information
Journal of Plasma Physics , Volume 88 , Issue 1 , February 2022 , 905880111
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aydemir, A.Y. 1992 Nonlinear studies of $m=1$ modes in high-temperature plasmas. Phys. Fluids B: Plasma Phys. 4 (11), 3469–3472.CrossRefGoogle Scholar
Biancalani, A. & Scott, B.D. 2012 Observation of explosive collisionless reconnection in 3d nonlinear gyrofluid simulations. Europhys. Lett. 97 (1), 15005.CrossRefGoogle Scholar
Brizard, A. 1992 Nonlinear gyrofluid description of turbulent magnetized plasmas. Phys. Fluids B: Plasma Phys. 4 (5), 1213–1228.CrossRefGoogle Scholar
Cafaro, E., Grasso, D., Pegoraro, F., Porcelli, F. & Saluzzi, A. 1998 Invariants and geometric structures in nonlinear Hamiltonian magnetic reconnection. Phys. Rev. Lett. 80, 4430–4433.CrossRefGoogle Scholar
Comisso, L., Grasso, D., Tassi, E. & Waelbroeck, F.L. 2012 Numerical investigation of a compressible gyrofluid model for collisionless magnetic reconnection. Phys. Plasmas 19, 042103.CrossRefGoogle Scholar
Comisso, L., Grasso, D., Waelbroeck, F.L. & Borgogno, D. 2013 Gyro-induced acceleration of magnetic reconnection. Phys. Plasmas 20 (9), 092118.CrossRefGoogle Scholar
Del Sarto, D., Califano, F. & Pegoraro, F. 2003 Secondary instabilities and vortex formation in collisionless-fluid magnetic reconnection. Phys. Rev. Lett. 91 (23), 235001.CrossRefGoogle ScholarPubMed
Del Sarto, D., Califano, F. & Pegoraro, F. 2006 Electron parallel compressibility in the nonlinear development of two-dimensional collisionless magnetohydrodynamic reconnection. Mod. Phys. Lett. B 20 (16), 931–961.CrossRefGoogle Scholar
Dorland, W. & Hammett, G.W. 1993 Gyrofluid turbulence models with kinetic effects. Phys. Fluids B: Plasma Phys. 5 (3), 812–835.CrossRefGoogle Scholar
Eastwood, J.P., Mistry, R., Phan, T.D., Schwartz, S.J., Ergun, R.E., Drake, J.F., Øieroset, M., Stawarz, J.E., Goldman, M.V., Haggerty, C., et al. 2018 Guide field reconnection: exhaust structure and heating. Geophys. Res. Lett. 45 (10), 4569–4577.CrossRefGoogle ScholarPubMed
Fitzpatrick, R. 2010 Magnetic reconnection in weakly collisional highly magnetized electron-ion plasmas. Phys. Plasmas 17 (4), 042101.CrossRefGoogle Scholar
Fitzpatrick, R. & Porcelli, F. 2004 Collisionless magnetic reconnection with arbitrary guide field. Phys. Plasmas 11 (10), 4713–4718.CrossRefGoogle Scholar
Fitzpatrick, R. & Porcelli, F. 2007 Erratum: collisionless magnetic reconnection with arbitrary guide-field [phys. plasmas 11, 4713 (2004)]. Phys. Plasmas 14 (4), 049902.CrossRefGoogle Scholar
Furth, H.P. 1962 Nucl. fusion suppl. Plasma Phys. Control. Fusion 1, 169.Google Scholar
Furth, H.P. 1964In Rendiconti della Scuola Internazionale di Fisica Enrico Fermi: Corso XXV : Teoria dei Plasmi. (ed. M.N. Rosenbluth). Academic Press.Google Scholar
Furth, H.P., Killeen, J. & Rosenbluth, M.N. 1963 Finite resistivity instabilities of a sheet pinch. Phys. Fluids 6, 459.CrossRefGoogle Scholar
Geller, M. & Ng, E.W. 1969 A table of integrals of exponential integral. J. Res. Natl Bur. Stand. B: Math. Sci. 73B (3), 191.CrossRefGoogle Scholar
Grasso, D., Califano, F., Pegoraro, F. & Porcelli, F. 2001 Phase mixing and saturation in Hamiltonian reconnection. Phys. Rev. Lett. 86, 5051–5054.CrossRefGoogle ScholarPubMed
Grasso, D., Margheriti, L., Porcelli, F. & Tebaldi, C. 2006 Magnetic islands and spontaneous generation of zonal flows. Plasma Phys. Control. Fusion 48 (9), L87–L95.CrossRefGoogle Scholar
Grasso, D., Ottaviani, M. & Porcelli, F. 2002 Growth and stabilization of drift-tearing modes in weakly collisional plasmas. Nucl. Fusion 42 (9), 1067–1074.CrossRefGoogle Scholar
Grasso, D., Pegoraro, F., Porcelli, F. & Califano, F. 1999 Hamiltonian magnetic reconnection. Plasma Phys. Control. Fusion 41 (12), 1497–1515.CrossRefGoogle Scholar
Grasso, D. & Tassi, E. 2015 Hamiltonian magnetic reconnection with parallel electron heat flux dynamics. J. Plasma Phys. 81 (5), 495810501.CrossRefGoogle Scholar
Grasso, D., Tassi, E. & Waelbroeck, F.L. 2010 Nonlinear gyrofluid simulations of collisionless reconnection. Phys. Plasmas 17 (8), 082312.CrossRefGoogle Scholar
Keramidas Charidakos, I., Waelbroeck, F.L. & Morrison, P.J. 2015 A Hamiltonian five-field gyrofluid model. Phys. Plasmas 22, 112113.CrossRefGoogle Scholar
Lele, S.K. 1992 Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 103 (1), 16–42.CrossRefGoogle Scholar
Man, H., Zhou, M., Yi, Y., Zhong, Z., Tian, A., Deng, X.H., Khotyaintsev, Y., Russell, C.T. & Giles, B. 2020 Observations of electron-only magnetic reconnection associated with macroscopic magnetic flux ropes. Geophys. Res. Lett. 47 (19), e2020GL089659.CrossRefGoogle Scholar
Mandell, N.R., Dorland, W. & Landreman, M. 2018 Laguerre–Hermite pseudo-spectral velocity formulation of gyrokinetics. J. Plasma Phys. 84 (1), 905840108.CrossRefGoogle Scholar
Morrison, P.J. 1998 Hamiltonian description of the ideal fluid. Rev. Mod. Phys. 70, 467–521.CrossRefGoogle Scholar
Numata, R., Dorland, W., Howes, G., Loureiro, N., Rogers, B. & Tatsuno, T. 2011 Gyrokinetic simulations of the tearing instability. Phys. Plasmas 18 (11), 112106.CrossRefGoogle Scholar
Numata, R. & Loureiro, N.F. 2015 Ion and electron heating during magnetic reconnection in weakly collisional plasmas. J. Plasma Phys. 81 (2), 305810201.CrossRefGoogle Scholar
Ottaviani, M. & Porcelli, F. 1993 Nonlinear collisionless magnetic reconnection. Phys. Rev. Lett. 71, 3802–3805.CrossRefGoogle ScholarPubMed
Passot, T., Sulem, P.L. & Tassi, E. 2018 Gyrofluid modeling and phenomenology of low- $\beta _e$ Alfvén wave turbulence. Phys. Plasmas 25 (4), 042107.CrossRefGoogle Scholar
Porcelli, F. 1991 Collisionless $m=1$ tearing mode. Phys. Rev. Lett. 66, 425–428.CrossRefGoogle ScholarPubMed
Schekochihin, A.A., Cowley, S.C., Dorland, W., Hammett, G.W., Howes, G.G., Quataert, E. & Tatsuno, T. 2009 Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas. Astrophys. J. Suppl. 182 (1), 310–377.CrossRefGoogle Scholar
Schep, T.J., Pegoraro, F. & Kuvshinov, B.N. 1994 Generalized two-fluid theory of nonlinear magnetic structures. Phys. Plasmas 1, 2843–2851.CrossRefGoogle Scholar
Tassi, E. 2017 Hamiltonian closures in fluid models for plasmas. Eur. Phys. J. D 71, 269.CrossRefGoogle Scholar
Tassi, E. 2019 Hamiltonian gyrofluid reductions of gyrokinetic equations. J. Phys. A: Math. Theor. 52 (46), 465501.CrossRefGoogle Scholar
Tassi, E., Grasso, D., Borgogno, D., Passot, T. & Sulem, P. 2018 A reduced Landau-gyrofluid model for magnetic reconnection driven by electron inertia. J. Plasma Phys. 84 (4), 725840401.CrossRefGoogle Scholar
Tassi, E., Passot, T. & Sulem, P.L. 2020 A Hamiltonian gyrofluid model based on a quasi-static closure. J. Plasma Phys. 86 (4), 835860402.CrossRefGoogle Scholar
Waelbroeck, F.L., Hazeltine, R.D. & Morrison, P.J. 2009 A Hamiltonian electromagnetic gyrofluid model. Phys. Plasmas 16, 032109.CrossRefGoogle Scholar
Waelbroeck, F.L. & Tassi, E. 2012 A compressible Hamiltonian electromagnetic gyrofluid model. Commun. Nonlinear Sci. Numer. Simul. 17, 2171.CrossRefGoogle Scholar