Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T05:40:38.794Z Has data issue: false hasContentIssue false
  • English
  • Français

Collisional alpha transport in a weakly rippled magnetic field

Part of: Focus on Fusion

Published online by Cambridge University Press:  04 April 2019

Peter J. Catto
Peter J. Catto*
Affiliation:
Plasma Science and Fusion Center, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
*
†Email address for correspondence: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To properly treat the collisional transport of alpha particles due to a weakly rippled tokamak magnetic field the tangential magnetic drift due to its gradient (the 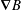$\unicode[STIX]{x1D735}B$ drift) and pitch angle scatter must be retained. Their combination gives rise to a narrow boundary layer in which collisions are able to match the finite trapped response to the ripple to the vanishing passing response of the alphas. Away from this boundary layer collisions are ineffective. There the 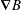$\unicode[STIX]{x1D735}B$ drift of the alphas balances the small radial drift of the trapped alphas caused by the ripple. A narrow collisional boundary layer is necessary since this balance does not allow the perturbed trapped alpha distribution function to vanish at the trapped–passing boundary. The solution of this boundary layer problem allows the alpha transport fluxes to be evaluated in a self-consistent manner to obtain meaningful constraints on the ripple allowable in a tokamak fusion reactor. A key result of the analysis is that collisional alpha losses are insensitive to the ripple near the equatorial plane on the outboard side where the ripple is high. As the high field side ripple is normally very small, collisional 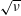$\sqrt{\unicode[STIX]{x1D708}}$ ripple transport is unlikely to be a serious issue.

Keywords

fusion plasmaplasma confinement
Type
Research Article
Information
Journal of Plasma Physics , Volume 85 , Issue 2 , April 2019 , 905850203
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Boozer, A. H. 1981 Plasma equilibrium with rational magnetic surfaces. Phys. Fluids 24, 1999–2003.Google Scholar
Calvo, I., Parra, F. I., Velasco, J. L. & Alonso, J. A. 2017 The effect of tangential drifts on neoclassical transport in stellarators close to omnigeneity. Plasma Phys. Control. Fusion 59, 055014, 19pp.Google Scholar
Catto, P. J. 2018 Ripple modifications to alpha transport in tokamaks. J. Plasma Phys. 84, 905840508, 39pp; 2019 Ripple modifications to alpha transport in tokamaks – CORRIGENDUM. J. Plasma Phys. 85, 945850101, 2pp.Google Scholar
Galeev, A. A., Sagdeev, R. Z., Furth, H. P. & Rosenbluth, M. N. 1969 Plasma diffusion in a toroidal stellarator. Phys. Rev. Lett. 22, 511–514.Google Scholar
Goldston, R. J., White, R. B. & Boozer, A. H. 1981 Confinement of high-energy trapped particles in tokamaks. Phys. Rev. Lett. 47, 647–649.Google Scholar
Gradshteyn, I. S. & Ryzhik, I. M. 2007 Table of Integrals, Series, and Products, 7th edn. p. 878. Elsevier/Academic.Google Scholar
Ho, D. D.-M. & Kulsrud, R. M. 1987 Neoclassical transport in stellarators. Phys. Fluids 30, 442–461.Google Scholar
Hsu, C. T., Catto, P. J. & Sigmar, D. J. 1990 Neoclassical transport of isotropic fast ions. Phys. Fluids B 2, 280, 11pp.Google Scholar
Linsker, R. & Boozer, A. H. 1982 Banana drift transport in tokamaks with ripple. Phys. Fluids 25, 143–147.Google Scholar
Magnus, W., Oberhettinger, F. & Soni, R. P. 1966 Formulas and Theorems for the Special Functions of Mathematical Physics, p. 9. Springer.Google Scholar
Mynick, H. E. 1986 Generalized banana-drift transport. Nucl. Fusion 26, 491–506.Google Scholar
Redi, M. H., Budny, R. V., McCune, D. C., Miller, C. O. & White, R. B. 1996 Simulations of alpha particle ripple loss from the international thermonuclear experimental reactor. Phys. Plasmas 3, 3037–3042.Google Scholar
White, R. B. 2001 The Theory of Toroidally Confined Plasmas, 2nd edn. pp. 298–302. Imperial College Press.Google Scholar
White, R. B., Goldston, R. J., Redi, M. H. & Budny, R. V. 1996 Ripple-induced energetic particle loss in tokamaks. Phys. Plasmas 3, 3043–3054.Google Scholar
Yushmanov, P. N. 1982 Thermal conductivity due to ripple-trapped ions in a tokamak. Nucl. Fusion 22, 315–324.Google Scholar
Yushmanov, P. N. 1983 Generalized ripple-banana transport in a tokamak. Nucl. Fusion 23, 1599–1612.Google Scholar